奇异分数阶复杂动态网络的鲁棒同步:LMI法

张会珍,刘宝江,邵克勇,任伟建

0 引 言

复杂网络广泛存在于现实生活中,神经网络、电力网络、社交网络和交通网络等实际问题都可抽象为复杂网络进行研究。随数学理论与非线性控制理论的快速发展,学者们发现许多复杂非线性系统都可通过网络进行描述,将复杂网络分解成若干个节点,而节点与节点之间展现非线性动力学行为。虽然早在18世纪数学家Eüler提出的七桥问题的数学图论可看做是最早复杂网络,但复杂网络的真正热潮产生于20世纪末。Watts等[1]在Nature发表的文章提出复杂网络的小世界特性,Bαrαbα'si等[2]在Science提出的无标度网络模型为新世纪复杂网络的研究展现了更为广阔的空间。国内学者的研究在这段时期也取得了丰富的成果。汪小帆等[3]与何大韧等[4]的著作不仅促进了复杂网络研究的发展、传播,更为以后中国学者的研究奠定了坚实的基础。

复杂网络的复杂性主要体现在结构、节点的复杂以及不确定因素的影响。众多学者不仅对其特有的属性进行研究,对网络的动态特性也产生了浓厚的兴趣,如网络的结构变化、加入控制器后网络的影响变化以及同步变化[5-7]。尤其近几年国内外涌现了大量关于复杂网络同步的优秀论文,如完全同步、延迟同步、投影同步、自适应同步以及脉冲同步等。文献[8]基于线性耦合的网络研究网络系统同步的稳定性问题,并获得了主稳定函数判据。文献[9]对具有相似节点的耦合时滞复杂网络的稳定性与同步控制进行了分析。

随近几年复杂网络的深入研究,传统整数阶微分方程建模已不能满足目前需求,人们迫切需求更好的建模数学工具刻画研究对象,这时分数阶微积分走入了众多学者的视线。因为复杂网络节点往往是非线性动力系统,系统可能具有混沌、分岔等复杂的动力学行为,这些系统用分数阶微积分描述更为准确实际。尽管关于分数阶混沌系统的同步和控制已经有了一些研究结果[10-12],但由于分数阶微分系统的稳定性理论远没有整数阶系统的稳定性理论成熟,复杂网络结构的复杂性以及结点行为的多样性等因素,使关于分数阶复杂网络的同步和控制的研究结果还很缺乏。文献[13]根据最新的分数阶微分系统的稳定性理论,通过LMI法给出了分数阶复杂网络系统的稳定条件。文献[14,15]分别研究了星型耦合分数阶复杂网络的同步与环状分数阶复杂网络的同步。文献[16]基于分数阶线性微分系统的鲁棒稳定性判别方法,研究了具有不确定性分数阶复杂网络的鲁棒同步等。

奇异系统又称为广义系统、隐式系统或微分代数系统。20世纪70年代初,Rosenbrock[17]首次提出线性广义系统,研究系统受限等价性,状态空间模型的描述方式的提出使整数阶奇异系统理论得到了长足的发展。作为与正常系统相对应的奇异系统,因为其不仅包含正常系统所具有的指数解还包含其不具有的脉冲解与静态解。这为解决工程实际问题提供了更精确的模型同时在处理上也带来了新的难度。张庆灵等[18]作为国内奇异系统的先驱,先后出版多部关于奇异系统专著,极大的促进了奇异系统理论的发展。相较分数阶系统的稳定性理论,关于奇异分数阶系统的稳定性分析更是少之又少。文献[19]给出了奇异分数阶系统正则性,无脉冲性及容许性的定义,并提出线性奇异分数阶系统容许性的充分必要条件。文献[20]通过引用基本有界定理给出了带有内部扰动非线性奇异分数阶不确定系统的鲁棒稳定性条件。文献[21]通过李雅普诺夫直接法给出了非线性奇异分数阶复杂网络系统的同步条件。文献[22]提出了一种频率分布分数阶积分器等效模型,提出了针对线性、非线性、离散型微分方程的间接李雅普诺夫方法,避免计算李雅普诺夫函数的分数阶导数。文献[23]通过引用上述的非线性连续频率分布等价模型,结合间接李雅普诺夫方法给出了不确定分数阶非线性复杂网络系统在观测器下的鲁棒稳定的充分条件。

笔者通过设计同步控制器将奇异系统转化为正常系统。同样引用文献[22]的非线性连续频率分布等价模型,结合间接李雅普诺夫方法,构造了全新的李雅普诺夫函数,并利用Matlab的LMI工具箱,给出奇异分数阶复杂网络误差系统(0＜α＜1)渐近稳定的充分条件,从而得到奇异分数阶复杂网络动态系统的同步条件。

1 分数阶微积分定义及引用定理

下面给出一些应用的定义及引理。

定义1 Riemann-Liouville分数阶积分的定义描述[24]

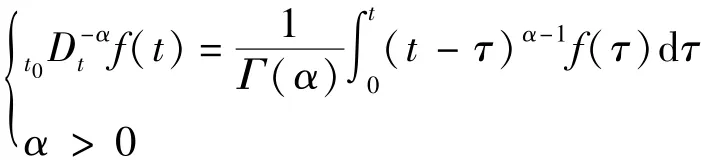
定义2 Riemann-Liouville分数阶导数定义为[24]

其中m∈Z+。

定义3 若h(t)是一个线性系统的脉冲响应,h(t)与其扩散表达式μ(ω)有如下关系[21]

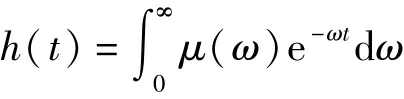
分数阶的积分算子t0D-αtf(t)可写成

其中*表示卷积运算。

h(t)的扩散表达式为 μ(ω)=sin(απ)/πω-α。

引理1 分数阶线性微分方程[24]

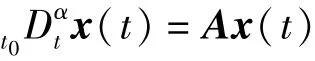
等价于

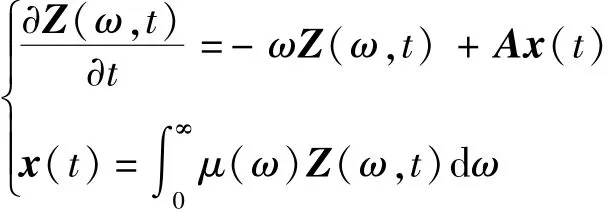
引理2 对于任意适当维数的实矩阵X,Y,有[24]

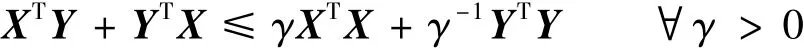
1)S＜0;

2)S11＜0,S22-ST12S-111S12＜0;

3)S22＜0,S11-S12S-122ST12＜0。

引理4 若A∈Cn×n是复矩阵。当且仅当存在一个对称非奇异矩阵X∈Cn×n,使AX+X*A*＜0(*表示矩阵的共轭转置),则A为非奇异矩阵[15]。

考虑如下奇异分数阶复杂网络驱动系统

其中0＜α＜1,x(t)=[xi1(t) xi2(t) … xin(t)]T∈Rn,是第i个节点的状态向量。ΔA代表系统的参数扰动,ΔA=MΔN,Δ的元为Lebesgue可测且满足ΔTΔ≤I。A,M,N是适当维数的常数矩阵,Γ为内部耦合矩阵。 E∈Rn×n是奇异矩阵,rank(E)=r＜n。 f:Rn→Rn表示网络节点动力学函数,G=(gij)∈Rn×n表示耦合网络的拓扑结构,满足gij=0(i=j),gij＞0(i≠j)。

对角元素定义为

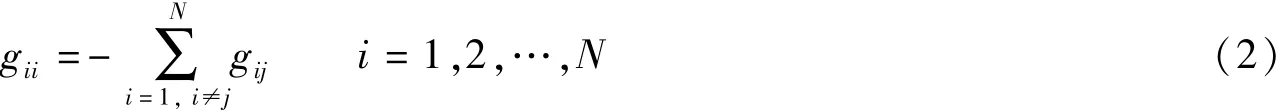
假设系统(1)的输出为s(xi(t)),根据非线性观测器的设计方法[22],则传递同步信号形式如下

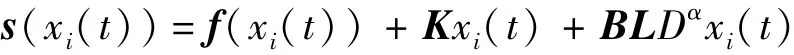
其中K∈Rn×n,L∈Rn是FO-PD控制器的增益,B是适当维数的常数矩阵。

奇异分数阶复杂网络响应系统为

第i个节点的实时误差为ei(t)=yi(t)-xi(t),若满足, 则复杂网络系统实现同步。

定义奇异分数阶复杂网络误差系统

即

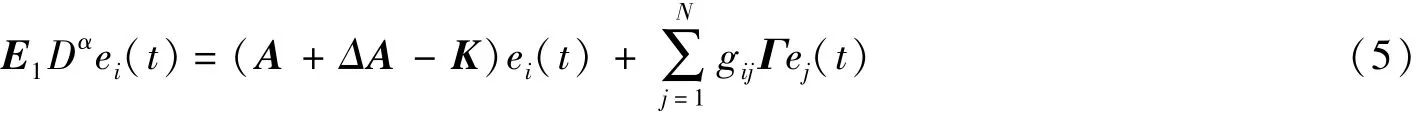
其中E1=E+BL。

式(1)中的E为非奇异矩阵,系统(5)可转化为正常系统的充分条件是rank[E B]=n。将奇异系统转化为正常系统(即非奇异系统)称为系统的正常化。任意正常系统都是正则的。

2 奇异分数阶复杂网络的同步分析

首先给出使系统正常化的增益矩阵L存在条件,然后求解增益K使正常系统渐近稳定。

定理1 若系统(5)可以转换为正常系统,当且仅当存在一个对称非奇异矩阵P和任意矩阵Y满足

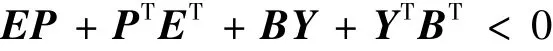
其中Y=LP。

证明 若式(5)可转化为正常系统,当且仅当存在L使E1=E+BL是非奇异的。根据引理4,有

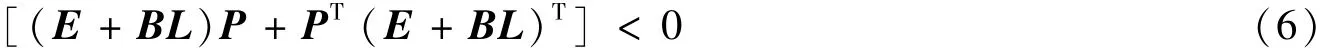
将Y=LP代入式(6),得证。证明完毕。

由于E1是非奇异的,即可逆,则误差系统(5)等价于

通过kronecker积,可得到

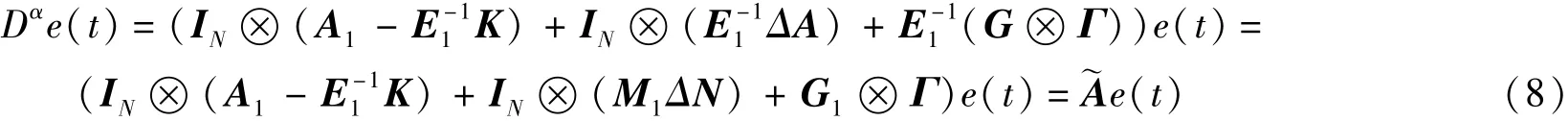
其中A1=(E+BL)-1A,M1=(E+BL)-1M,G1=(E+BL)-1G,～A=IN⊗(A1-E-11K)+IN⊗(M1ΔN)+G1⊗Γ。

定理2 奇异分数阶复杂网络驱动系统(1)与奇异分数阶复杂网络响应系统(3)同步,当且仅当存在正定对称矩阵P0,矩阵K以及ε＞0,满足

其中 Ω =sym{IN⊗P0A1}-sym{IN⊗P0E-11K}+sym{G1⊗P0Γ}+ε(IN⊗P0M1)(IN⊗P0M1)T,A1=(E+BL)-1A, M1=(E+BL)-1M, G1=(E+BL)-1G。

证明 根据引理1,系统(7)可转化为

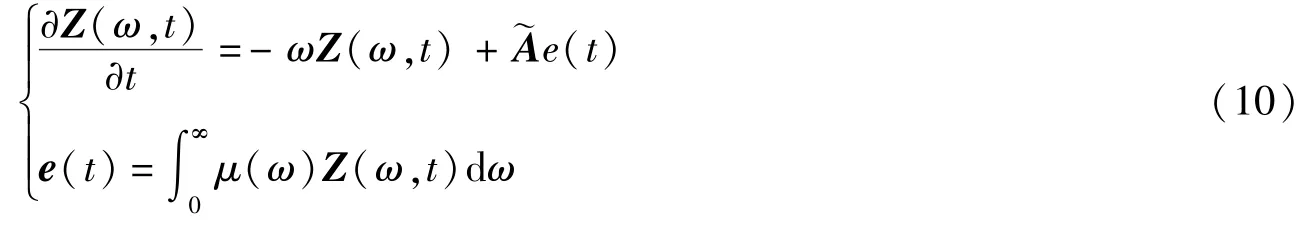
考虑两个李雅普诺夫函数:v(ω,t)是对应于基本频率ω的单边李雅普诺夫函数,v(t)是所有李雅普诺夫函数v(ω,t)=ZT(ω,t)PZ(ω,t)和权重函数μ(ω)的集合。因此,可定义单边李雅普诺夫函数

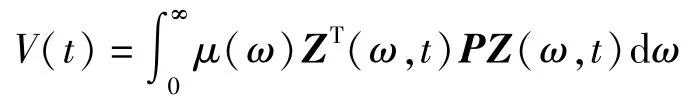
上述函数对时间t求导

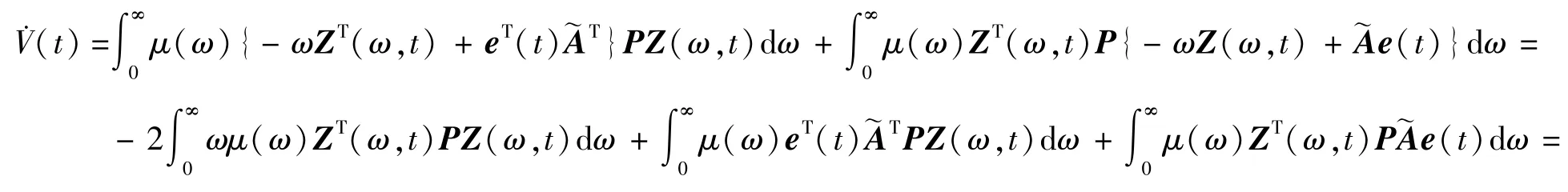
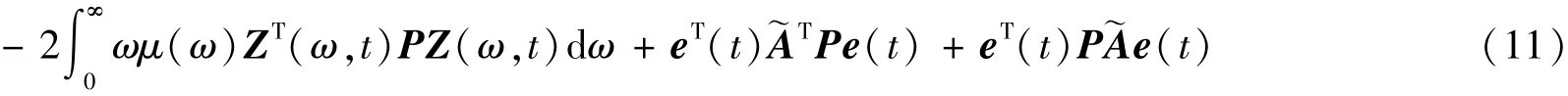
若eT(t)～ATPe(t)+eT(t)P～Ae(t)＜0,则˙V(t)＜0称闭环误差系统鲁棒稳定,即驱动系统(1)与响应系统(3)同步。

将～A展开得到

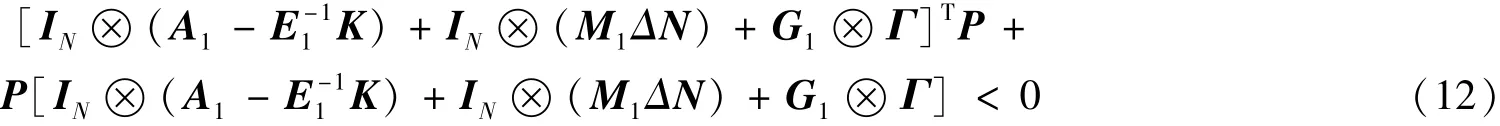
设P=IN⊗P0,代入式(12)化简得

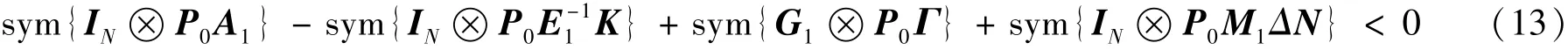
根据引理2,有

则式(13)化为

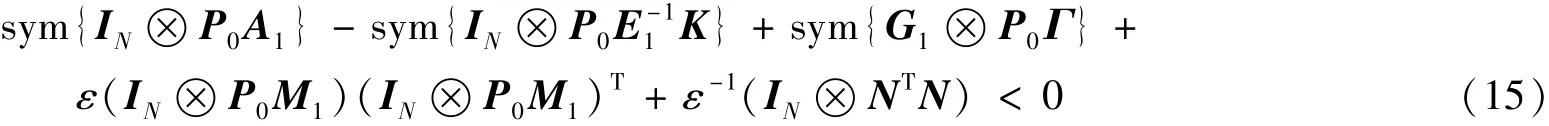
根据引理3得到不等式(9),证毕。

因定理2中包含P0E-11K的非线性项不能通过LMI工具箱直接求得,因此通过进行转换得到以下定理。

定理3 奇异分数阶复杂网络驱动系统(1)与奇异分数阶复杂网络响应系统(3)同步,当且仅当存在正定对称矩阵X,适当维数矩阵Q以及ε＞0,满足

其中

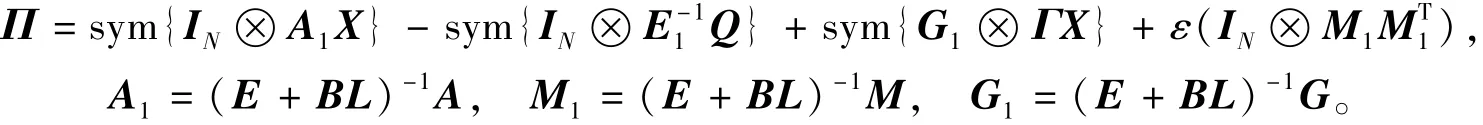
证明 对式(14)左右两边同时乘以IN⊗P-10,经过化简得

设X=P-10,Q=KX,得到式(16),证毕。

3 仿真算例

例1 考虑一个具有如下参量的非线性分数阶奇异系统

其中α=0.95。

对于奇异分数阶复杂网络动态系统

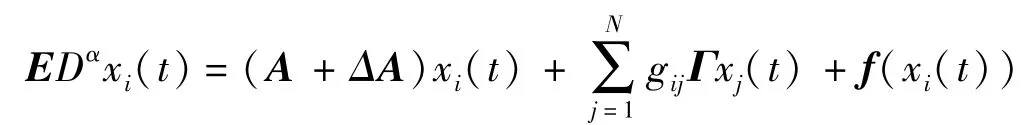
为了方便,取含3个节点的网络进行仿真。

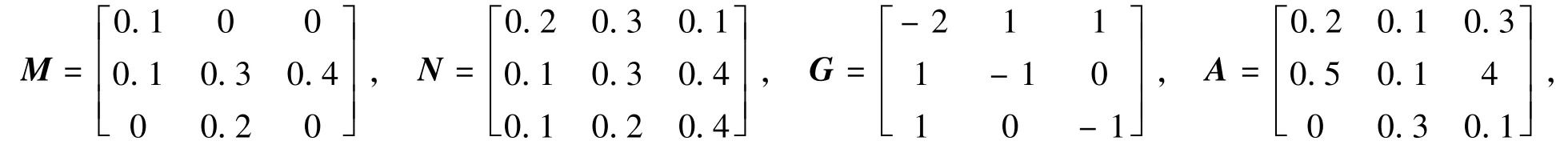
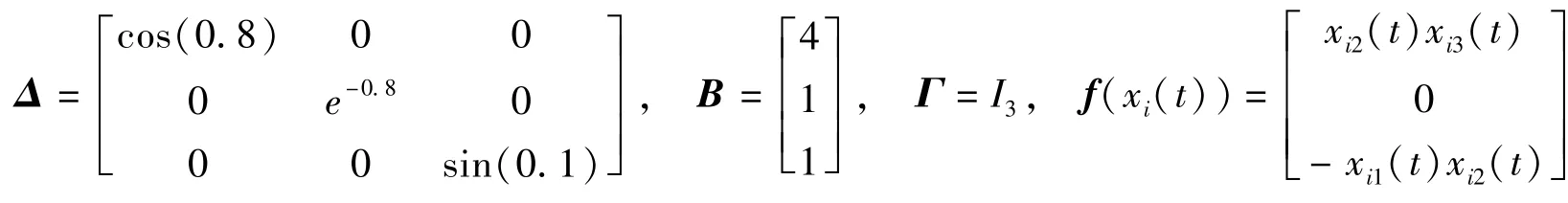
根据定理1,通过Matlab的LMI工具箱,分别得到P和Y

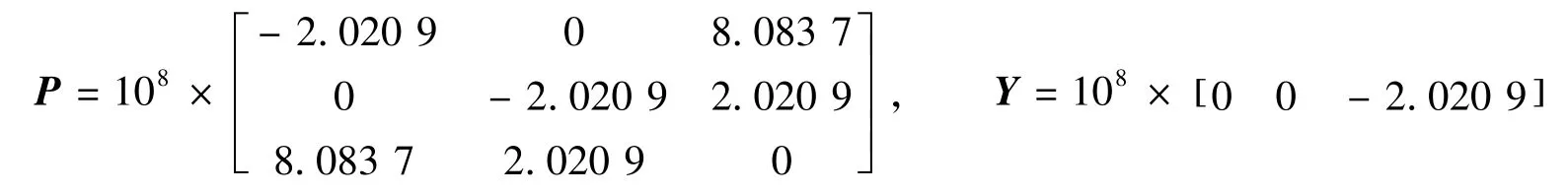
则增益

这表明系统(4)可正常化。根据此增益,可获得满足系统(7)的新矩阵

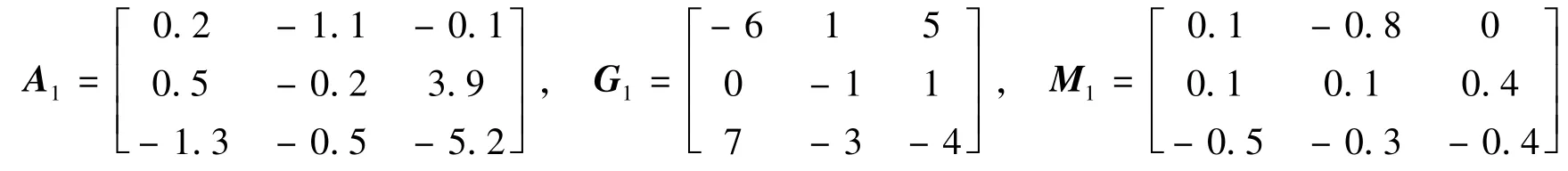
由定理3,通过Matlab的LMI工具箱,可分别得

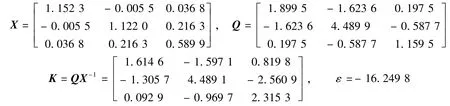
取节点初值xi0=[0 1 0],yi0=[-1 1 1],i=1,2,3。而完整的闭环奇异分数阶复杂网络误差系统ei1(t),ei2(t),ei3(t)随时间变化的状态轨迹曲线如图1～图3所示。从仿真结果可看出,奇异分数阶复杂网络误差系统达到渐近稳定,即奇异分数阶复杂网络驱动系统(1)与奇异分数阶复杂网络响应系统(3)同步。

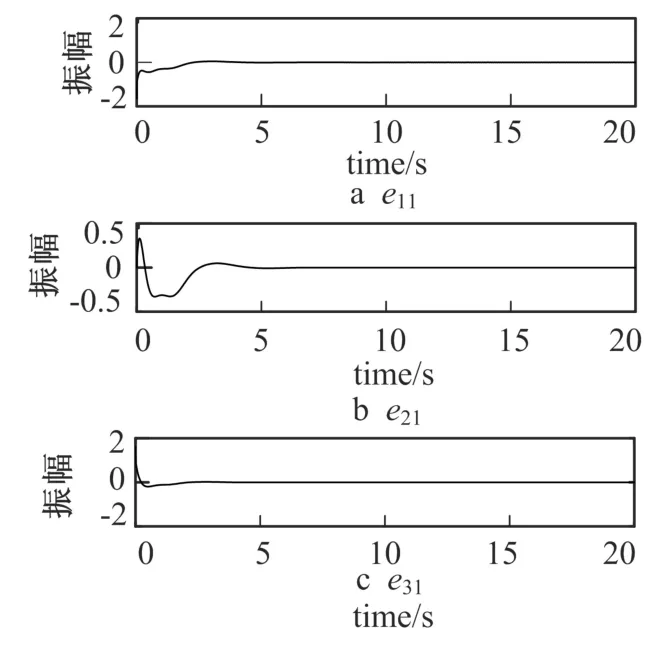
图1 误差系统ei1(t)状态响应图Fig.1 State response ei1(t)of errors system

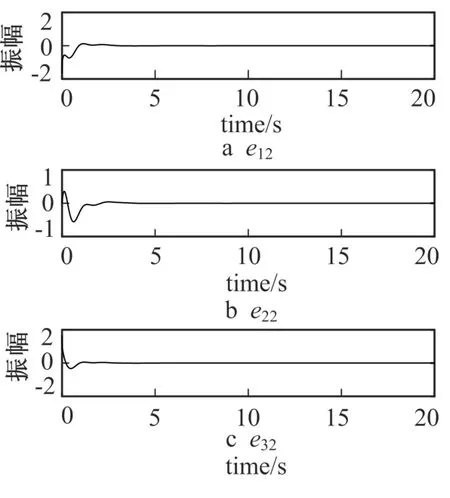
图2 误差系统ei2(t)状态响应图Fig.2 State response ei2(t)of errors system

图3 误差系统ei3(t)状态响应图Fig.3 State response ei3(t)of errors system

4 结 语

笔者通过引入连续频率分布等价模型,应用间接李雅普诺夫方法,构造了一个新的李雅普诺夫函数,给出了非线性奇异分数阶复杂动态网络(0＜α＜1)鲁棒同步的全新方法。设计了分数阶同步控制器,将奇异系统转化为正常系统,利用Matlab的LMI工具箱求出控制器的增益。最后通过数值仿真验证所提方法的有效性。

[1]WATTSD J,STROGATZ S H.Collective Dynamics of‘Small-World'Networks[J].Nature,1998,393(6684):440-442.

[2]BARABÁSI A L,ALBERT R.Emergence of Scaling in Random Networks[J].Science,1999,286(5439):509.

[3]汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006.WANG Xiaofan,LIXiang,CHEN Guanrong.Complex Network Theory and Its Application[M].Beijing:Tsinghua University Press,2006.

[4]何大韧,刘宗华,汪秉宏.复杂系统与复杂网络[M].北京:高等教育出版社,2009.HE Daren,LIU Zonghua,WANG Binghong.The Complex Systems and Complex Networks[M].Beijing:Higher Education Press,2009.

[5]GU Y Q,SHAO C,FU X C.Complete Synchronization and Stability of Star-Shaped Complex Networks[J].Chaos Solitons&Fractals,2006,28(2):480-488.

[6]FENG J,SUN S,XU C,et al.The Synchronization of General Complex Dynamical Network via Pinning Control[J].Nonlinear Dynamics,2011,67(2):1623-1633.

[7]WU X,LU H,LU H.Generalized Projective Synchronization between Two Different General Complex Dynamical Networks with Delayed Coupling[J].Physics Letters A,2010,374(38):3932-3941.

[8]PECORA L M,CARROLL T L.Master Stability Functions for Synchronized Coupled Systems[J].Physical Review Letters,1998,80(10):2109-2112.

[9]范永青,王银河,王青云,等.具有相似节点的耦合时滞复杂网络的稳定性与同步控制分析[J].控制与决策,2013,28(2):247-252.FAN Yongqing,WANG Yinhe,WANG Qingyun,et al.Control Analysis of the Stabilization and Synchronization of Coupling Time-Delay Complex Dynamical Networks with Similar Nodes[J].Control and Decision,2013,28(2):247-252.

[10]ZHU H,ZHOU S,HE Z.Chaos Synchronization of the Fractional-Order Chen's System[J].Chaos Solitons&Fractals,2009,41(5):2733-2740.

[11]TAVAZOEI M S,HAERI M.Synchronization of Chaotic Fractional-Order Systems via Active Sliding Mode Controller[J].Physica A Statistical Mechanics&Its Applications,2008,387(1):57-70.

[12]JIAO Z,ZHONG Y.Robust Stability for Fractional-Order Systems with Structured and Unstructured Uncertainties[J].Computers&Mathematics with Applications,2011,64(10):3258-3266.

[13]ZHANG H,WANG X,LIN X.Stability and Control of Fractional Chaotic Complex Networks with Mixed Interval Uncertainties[J].Asian Journal of Control,2017,19(1):106-115.

[14]WANG J,ZHANG Y.Network Synchronization in a Population of Star-Coupled Fractional Nonlinear Oscillators[J].Physics Letters A,2010,374(13/14):1464-1468.

[15]DELSHAD S S,ASHEGHAN M M,BEHESHTI M H.Synchronization of Non-Coupled Incommensurate Fractional Order Chaotic Systems with Ring Connection[J].Communications in Nonlinear Science&Numerical Simulation,2011,16(9):3815-3824.

[16]WONG W K,LI H,LEUNG SY S.Robust Synchronization of Fractional-Order Complex Dynamical Networks with Parametric Uncertainties[J].Communications in Nonlinear Science&Numerical Simulation,2012,17(12):4877-4890.

[17]ROSENBROCK H H.Structural Properties of Linear Dynamical Systems[J].International Journal of Control,1974,20(20):191-202.

[18]张庆灵,杨冬梅.不确定广义系统的分析与综合[M].沈阳:东北大学出版社,2003.ZHANG Qingling,YANG Dongmei.Uncertainty Analysis and Synthesis of Generalized Syste[M].Shenyang:Northeastern University Press,2003.

[19]YAO Y U,JIAO Z,SUN CY.Sufficient and Necessary Condition of Admissibility for Fractional-Order Singular System[J].Acta Automatica Sinica,2013,39(12):2160-2164.

[20]YIN C,ZHONG SM,HUANG X,et al.Robust Stability Analysis of Fractional-Order Uncertain Singular Nonlinear System with External Disturbance[J].Applied Mathematics&Computation,2015,269(C):351-362.

[21]LIU S,ZHOU X F,LI X,et al.Stability of Fractional Nonlinear Singular Systems and Its Applications in Synchronization of Complex Dynamical Networks[J].Nonlinear Dynamics,2016,84(4):1-9.

[22]TRIGEASSOU J C,MAAMRI N,SABATIER J,et al.A Lyapunov Approach to the Stability of Fractional Differential Equations[J].Signal Processing,2011,91(3):437-445.

[23]LAN Y H,GU H B,CHEN C X,et al.An Indirect Lyapunov Approach to the Observer-Based Robust Control for Fractional Order Complex Dynamic Networks[J].Neuro-Computing,2014,136(8):235-242.

[24]张会珍,刘宝江,邵克勇,等.不确定分数阶奇异系统鲁棒控制及稳定性分析 [J].吉林大学学报:信息科学版,2017,35(4):392-397.ZHANG Huizhen,LIU Baojiang,SHAO Keyong,et al.Robust Control and Stability Analysis of Uncertain Descriptor Fractional Order System[J].Journal of Jilin University:Information Science Edition,2017,35(4):392-397.