浅海舰船地震波识别方法研究

李 环,迟秀秀

(沈阳理工大学 信息科学与工程学院,沈阳 110159)

地震波是从震源产生的向周围传播的弹性波,分为体波和面波,而舰船地震波是沿着液-固界面传播的一类面波[1]。航行舰船是一个很大的振动和噪声源,其振动和噪声引起的压力波经由流体介质传播到海底,引起海底岩层振动,产生弹性波并向远处传播[2],这种舰船地震波和普通的地震波特性基本相同。实际上,当震源激发后,会受到地上和地下各种弹性介质的影响,使得采集到的地震波数据中含有规则干扰波和不规则干扰波,其中不规则干扰波具有随机性,且无规律可循[3],在很大程度上影响了舰船地震波识别的准确性。

近年来,国内外不少学者从不同的角度对舰船地震波识别方法进行了研究,但在完全消除干扰波方面都存在一定困难[1]。本文以雷克子波为舰船地震波模型,利用小波变换与多分辨率之间的关系,把小波变换和滤波器组结合在一起,构造出基于无限冲激响应滤波器组(IIR)具有舰船地震波波形特征,且消除干扰能力强的5阶Butterworth小波。

1 Butterworth小波设计原理

若设尺度函数和小波函数分别为φ(t)、φ(t),则二尺度差分方程为

式中:t为时间变量;i是从-～+的整数;k为正整数。由二尺度差分方程可得线性组合的平滑逼近权重h0k和离散细节权重h1k分别为

h0k=<φ10(t),φ0k(t)>

(2)

h1k=<φ10(t),φ0k(t)>

(3)

从文献[4]可知以上两个权重序列分别为信号的平滑逼近和离散细节信号的滤波器,即离散平滑逼近

(4)

离散细节信号

(5)

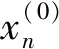
根据小波函数和尺度函数的一些性质[4],可以推导出由二尺度关系迭代出的尺度函数频域表达式为

(6)

(7)

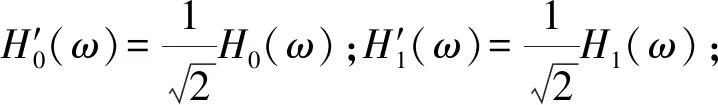
H(ω)是h(n)的频域形式。可以利用式(6)和式(7)推导出尺度函数和小波函数解析形式的解,但在通常情况下无法求解,只能通过对h(n)作迭代数值卷积来求尺度函数φ(t),进而通过φ(t)和φ(t)的联系推导出相应的φ(t)。

2 Butterworth小波的构造

利用正交的IIR滤波器组对可能解的结构进行全面检验,提出新的设计,在正交IIR滤波器组与小波联系的基础上,利用这些设计得到新的正交小波。Butterworth滤波器是常用的IIR滤波器,具有通带内最大平坦的幅频特性,且随着频率升高呈单调减的趋势,而常见的尺度函数都具有低通的幅频特性[5]。因此,利用上节所介绍的内容,通过Butterworth滤波器构造出具有舰船地震波波形特征的Butterworth小波。本文以5阶滤波器为例进行Butterworth小波设计。

所有正交有理双通道滤波器组在已知R(z)的情况下都可以表示成以下形式。

(8)

式中,P(z)是有理式;R(z)是因果对称的多项式。若R(z)的阶次是奇数(既长度为偶数)且因果系数对称,则将R(z)作奇偶分解,可表示为

R(z)=RE(z2)+z-1R0(z2)

(9)

式中RE(z2)和z-1R0(z2)分别是偶多项式和奇多项式。在因果且系数对称的多项式中,可将偶次项系数组成的序列时序反转再延迟N拍,便得奇次项序列,则可得

R(z)=RE(z2)+z-NRE(z-2)

(10)

将式(10)代入式(8)中可推导出

(11)

从文献[6]可知

H0(z)=A0(z)H(z)

(12)

H1(z)=z2k-1H0(-z-1)A1(z2)

(13)

式中:H0(z)和H1(z)分别为尺度函数和小波函数;H(z)是h(n)的Z变换形式;A0(z)和A1(z2)是任意全通系数,只对所实现的滤波器的相位有影响。

式(8)中P(z)又可写成

P(z)=H(z)H(z-1)

(14)

将式(12)代入式(14)可得

(15)

则当k=0,A0(z)=A1(z)=1时,由式(11)和式(15)恒等可得

(16)

H1(z)=z-1H0(-z-1)

(17)

根据正规性要求,设计的滤波器应在z=-1处有高阶零点,则有

R(z)=(1+z-1)N

(18)

当N=5时,将式(18)代入到式(16)中,可得

(19)

将式(19)代入式(17)可得

(20)

通过对式(19)分解可得

同理分解式(20)可得

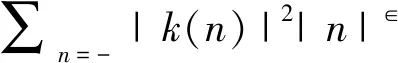
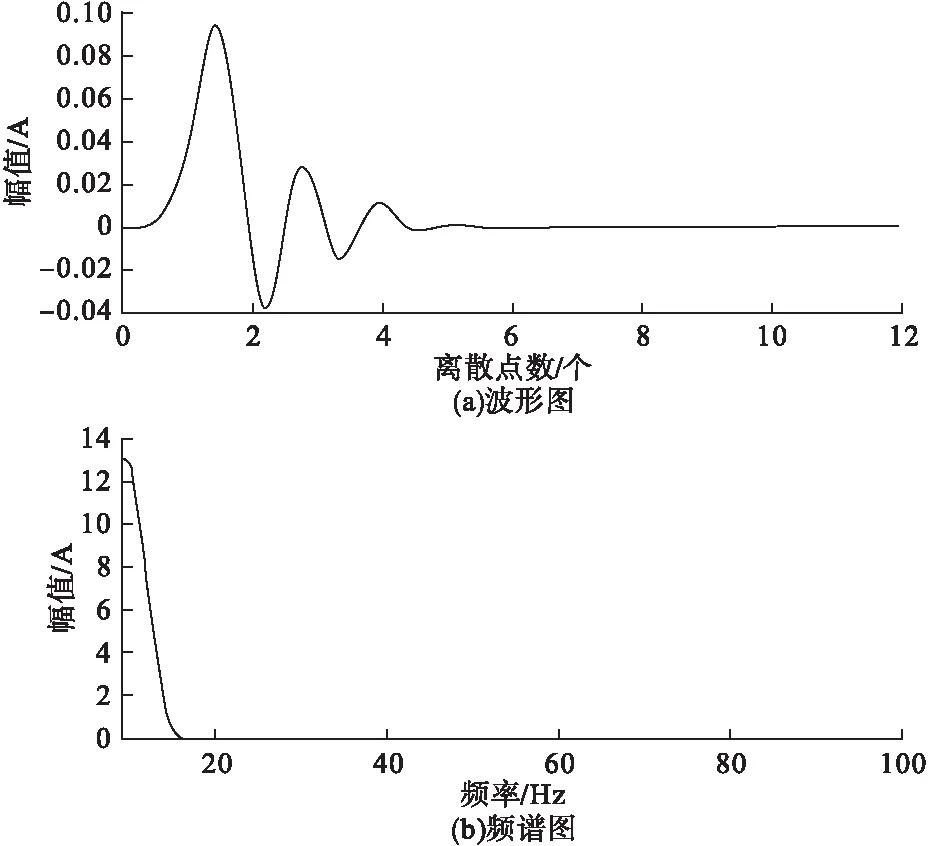
图1 Butterworth小波尺度函数波形图及频谱图

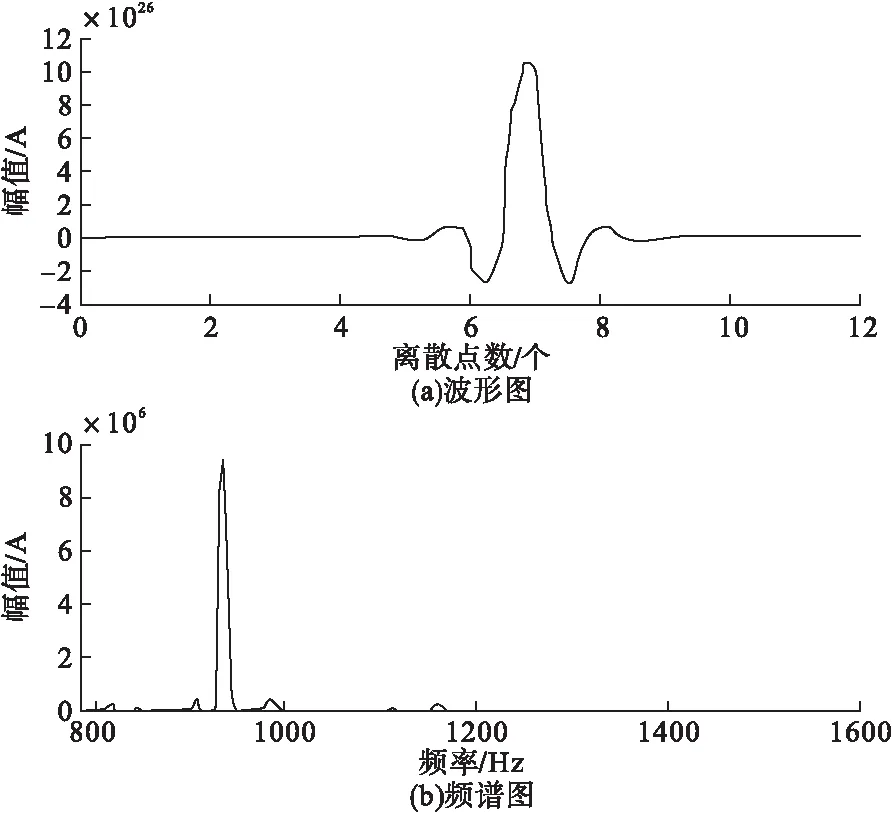
图2 Butterworth小波小波函数波形图及频谱图

3 舰船地震波提取实验

3.1 采集舰船地震波数据

利用500斤重4cm厚的钢板模拟舰船,当120斤重的铁锤敲击铁板激发地震波时,通过连接水下振动传感器的采集系统采集数据,地震波采集实验器材如表1所示。

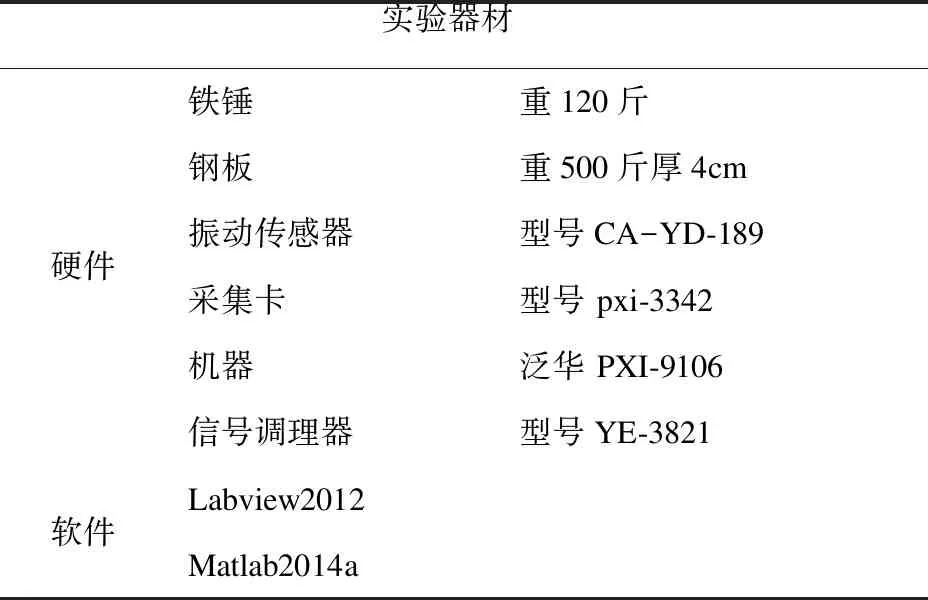
表1 实验器材

当幅值的测量范围为-5～5v,采样频率为2048Hz时,利用上述实验器材所采集到的原始地震波数据波形图及频谱图如图3所示。

因为面波的主要能量集中在10Hz到80Hz之间[2],观察图3b可知,本实验采集的数据包含舰船地震波信号,且有效舰船地震波的频率范围为0～50Hz。

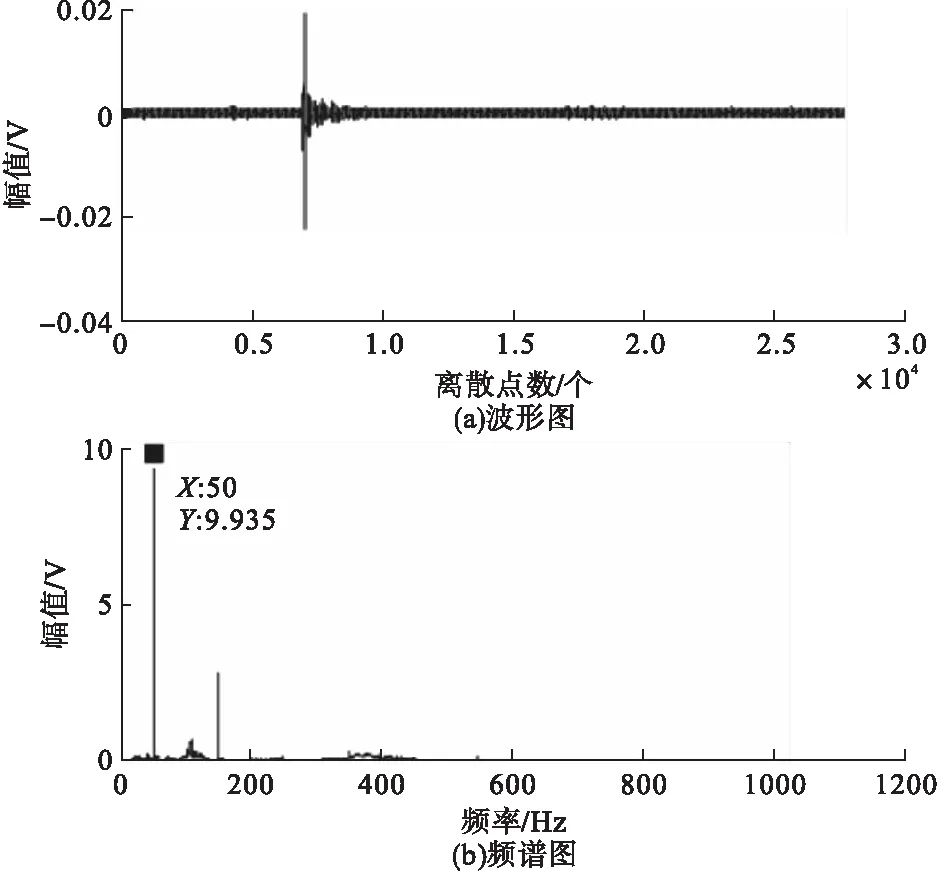
图3 原始地震波数据波形图及频谱图

3.2 Daubechies系列小波的舰船地震波提取

Daubechies系列小波是紧支撑正交小波,具有较好的正则性,与构造的Butterworth小波性质比较相似。由于原始地震波数据的采样频率为2048Hz,且本实验有效舰船地震波频率范围为0～50Hz,为获得全面且有效的信号,本文选用与所构造的Butterworth小波同阶的db5小波对原始地震波数据进行七层小波分解,db5小波七层滤波低频部分的结果如图4所示。

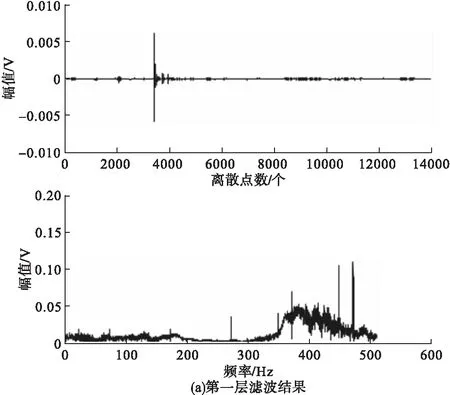
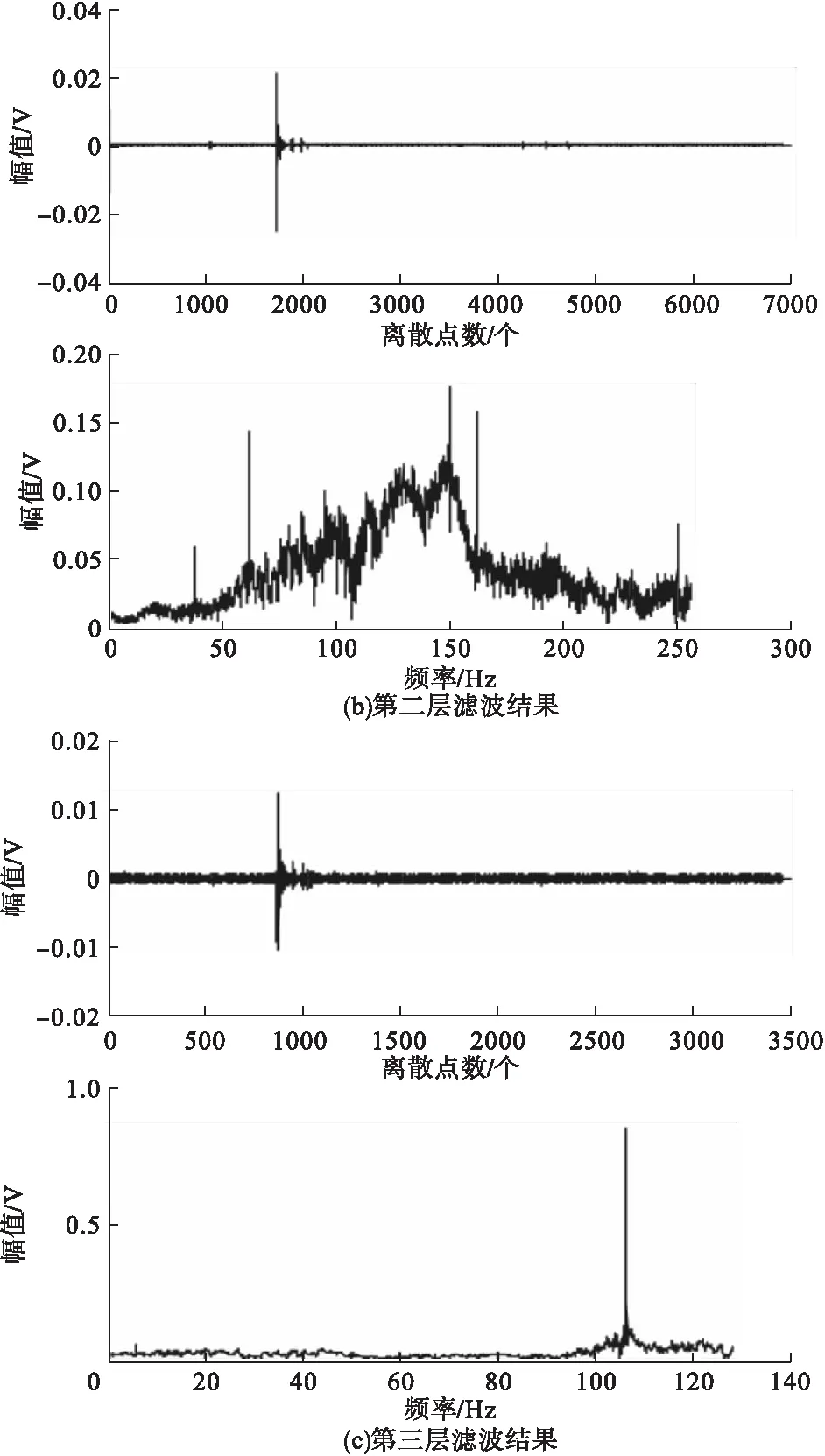
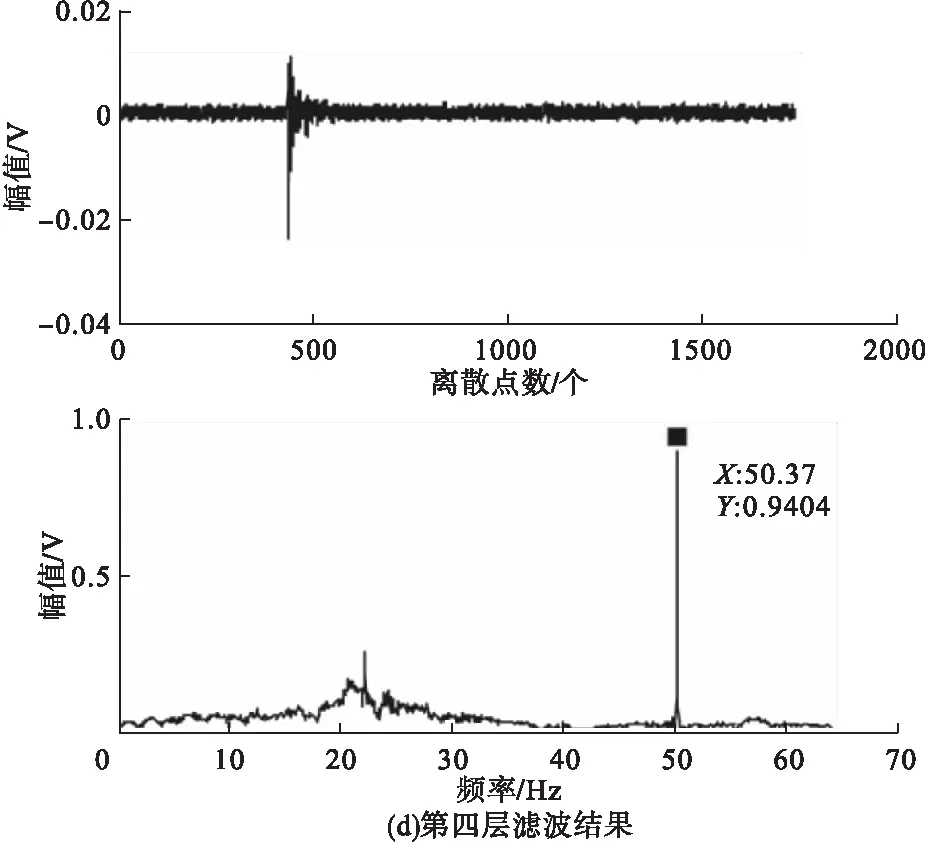
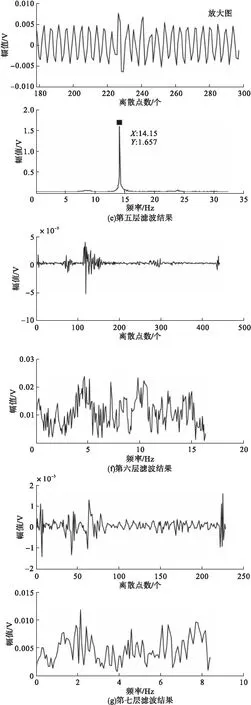
图4 db5小波七层滤波低频部分处理结果

观察db5小波七层滤波低频部分的结果可知,只有第五层、第六层和第七层的滤波结果范围为0～50Hz。对比图4f和图4g可知,随着分解层数的增加频谱分布越杂乱,干扰波与舰船地震波区分度越低;在图4e中经放大的时域图可观察到舰船地震波波形,且主要频率集中在14.15Hz处。

3.3 Butterworth小波的舰船地震波提取

从3.2节分析中可得,本实验的小波分解层数应为七层,因此本节利用所构造的Butterworth小波对原始地震波数据进行七层小波分解,构造的Butterworth小波七层滤波低频部分的结果如图5所示。

观察所构造的Butterworth小波七层滤波低频部分的结果可知,只有第五层、第六层和第七层频率为0～50Hz。对比图5e和图5g,可观察到频率主要集中在14.15Hz和2.148Hz处,且图5e中的信号滤波时消除高频干扰效果弱;在图5f的时域图中也可观察到舰船地震波波形,但频谱杂乱,干扰波和舰船地震波区分度低。

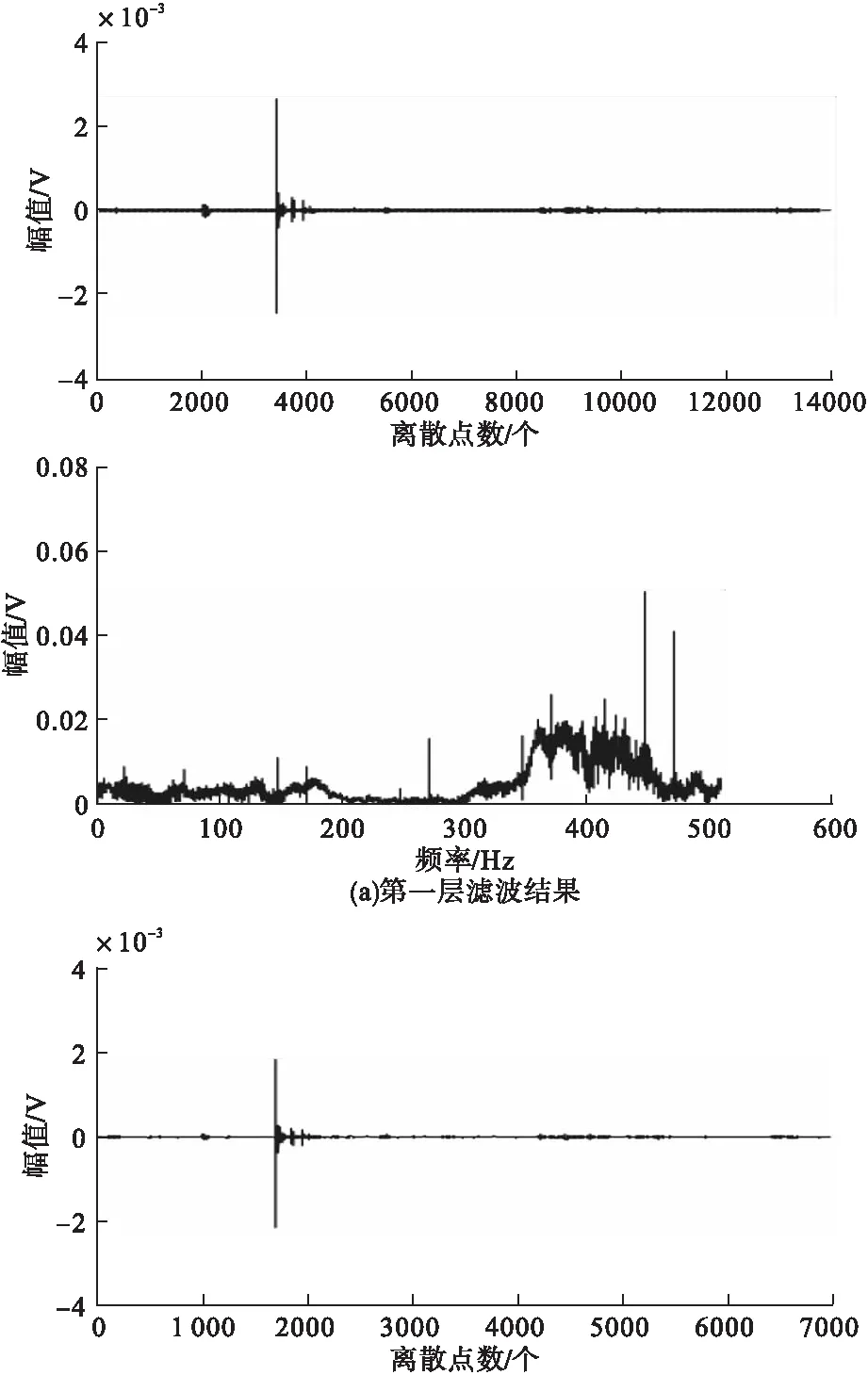
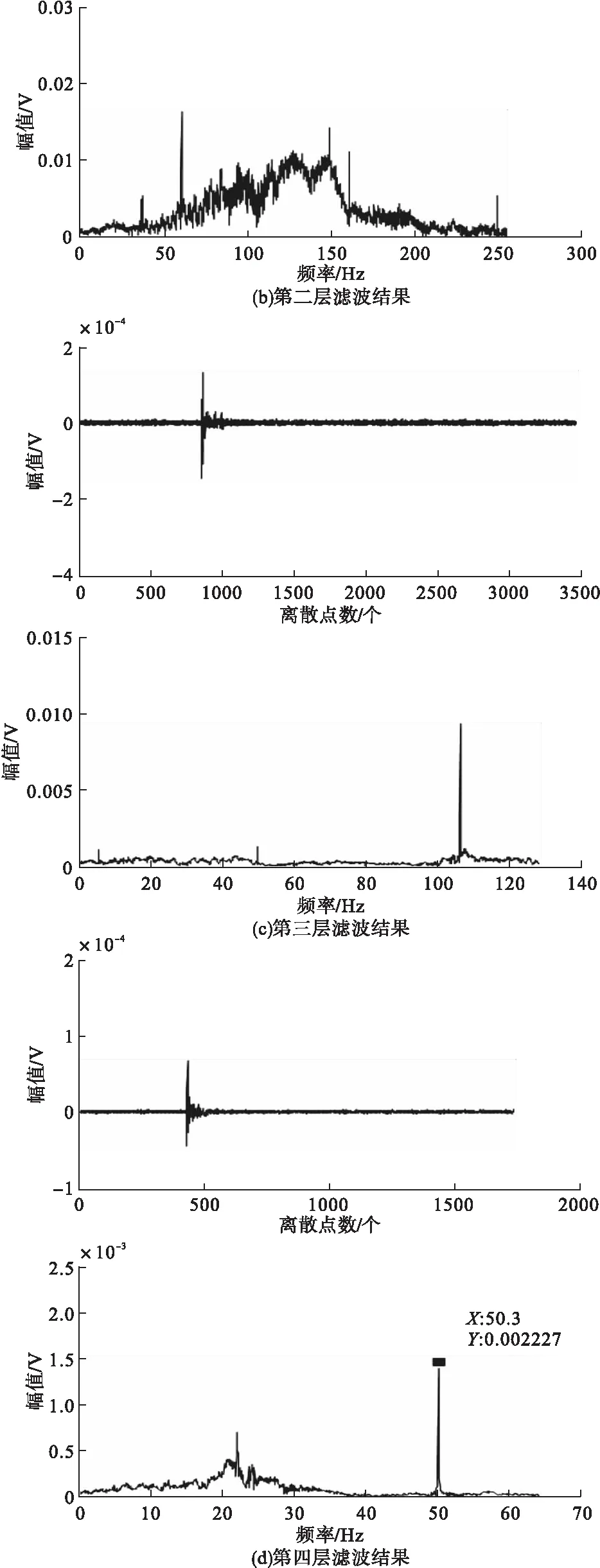
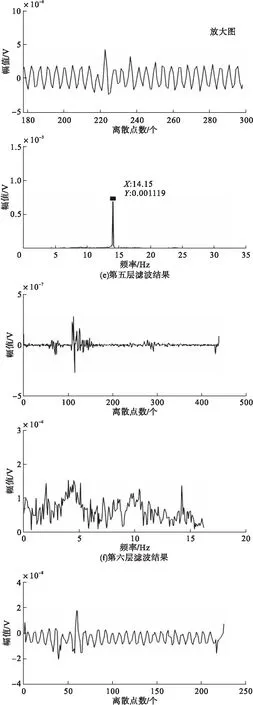
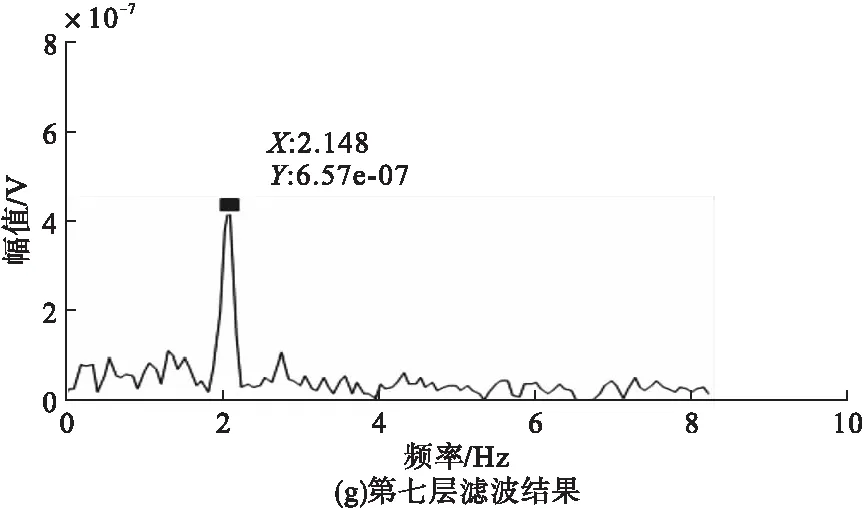
图5 Butterworth小波七层滤波低频部分处理结果

4 识别舰船地震波

为识别出滤波后信号中包含的有效舰船地震波信号,建立雷克子波的数学模型,雷克子波模拟瞬态脉冲式震源表达式为

F1(t)=A[1-2(πf)2(t-t0)2]e-(πf)2(t-t0)2

式中:A是幅值;f是主频;t是时间长度。当A=1、f=15Hz、t=100时,雷克子波数学模型如图6所示。

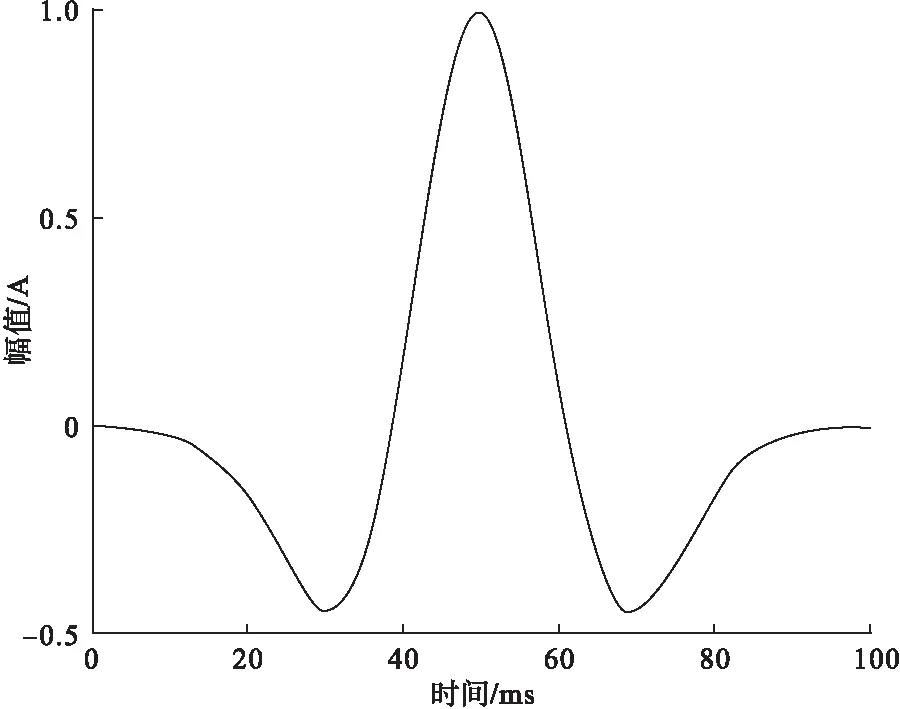
图6 雷克子波数学模型

互相关表示实际输出信号和理想输出信号的相似程度,即描述随机信号x(t)、y(t)在任意两个不同时刻t1、t2之间的相似程度[7]。因此将雷克子波数学模型作为x(t),滤波后信号作为y(t)。对比3.2节与3.3节的处理结果,可观察到两个小波第五层处理结果的频率都主要集中在14.15Hz处,且时域图波形特征非常相似。为避免选取的滤波层数不同对互相关运算结果的影响,选用Butterworth小波和db5小波第五层的结果作为y(t),将x(t)与y(t)做互相关运算,观察是否有最大值点。

Butterworth小波第五层滤波与雷克子波数学模型的互相关结果如图7所示,在第687个离散点时有互相关最大值,说明经过Butterworth小波处理后的信号中包含有效的舰船地震波信号。

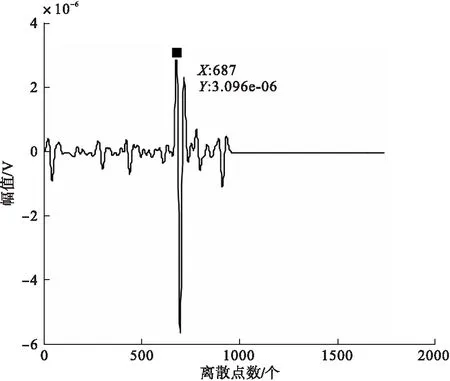
图7 Butterworth小波第五层滤波与雷克子波互相关结果

db5小波第五层滤波与雷克子波数学模型互相关的结果如图8所示。

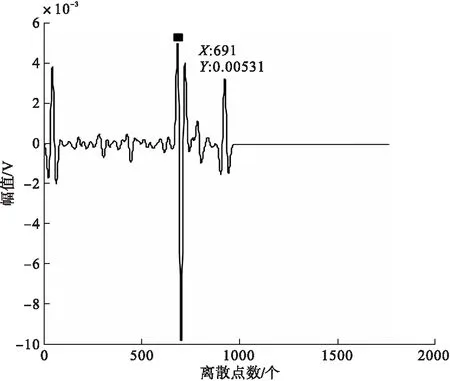
图8 db5小波第五层滤波与雷克子波互相关结果

由图8可以看出,在第691个离散点处有互相关最大值,说明经过db5小波处理后的信号中也包含有效的舰船地震波信号;但除了第691个离散点外,还有两个与雷克子波数学模型存在较高相关程度的点。

5 结论

(1)在满足有效舰船地震波频率范围的情况下,所构造的Butterworth小波可将原始地震波数据分层的频率范围降到10Hz以内,且可清晰观察到频率主要集中在2.148Hz处;db5小波只有当分层的频率在35Hz以内时,可清晰观察到频率主要集中在14.15Hz处,由此可得具有舰船地震波波形特征的Butterworth小波消除高频干扰能力强。

(2)从雷克子波数学模型分别与Daubechies系列小波和所构造的Butterworth小波滤波结果进行互相关后的对比分析中可知,两者的滤波结果中都包含有效舰船地震波信号,但Daubechies系列小波的滤波结果中存在两个与雷克子波数学模型具有较高相关程度的非雷克子波信号,故具有舰船地震波波形特征的Butterworth小波识别舰船地震波准确性高。