耿楼枢纽节制闸渗流场数值模拟分析

李新国

（河南固始县节能监察中心 固始 465200）

1 ABAQUS有限元软件简介

ABAQUS是由美国HKS公司（Hibbitt,Karlsson&Sorensen,INC.）开发的一款功能非常强大的有限元分析软件，可以分析各种固体力学、结构力学系统，特别是能够处理非常复杂的非线性问题。ABAQUS有限元软件主要包括ABAQUS/CAE前后处理模块以及两个分析模块（ABAQUS/Standard、ABAQUS/Explicit）。ABAQUS/CAE 是联系其他模块的纽带，使用者能够利用图形交互界面便捷的完成几何建模、赋予材料属性、定义约束条件和载荷作用、划分单元网格等操作，然后将模型提交给相应的分析模块进行计算分析，最后在ABAQUS/Viewer中查看计算结果并进行相应的后处理。ABAQUS完整的计算分析步骤为前处理、分析计算和后处理。

2 计算模型

2.1 孔压边界条件

考虑孔压边界条件时，将建筑物的临空面设为不透水边界，河道边坡及建基面设为透水边界，并根据上下游水位的不同，设定不同的初始孔隙水压力及初始浸润面。

在进行渗流稳定性分析时，通过设定不同的孔压边界条件来对不同运行工况的水位差进行模拟，同时根据ABAQUS软件的渗流计算流程，根据不同工况设定初始浸润面及下游临空面初始渗流流速，在迭代计算过程中将根据不同的孔压边界条件及位移边界条件做出相应的调整来实现对闸址区三维渗流场的模拟。模拟计算工况见表1。

2.2 几何模型

土体采用Mohr－Coulomb弹塑性模型。为了减小边界条件对计算结果的影响，取节制闸底面为Z=0剖面，分别取Z=15.9m及Z=-18.56m为计算模型的上下边界；取闸室上游起点处为X=0剖面，分别取X=130m及X=-304.5m为计算模型的前后边界；取节制闸中心线为Y=0剖面，分别取Y=-165m及Y=483m为计算模型的左右边界。对于位移边界条件，计算模型内的所有节点采用全约束；对于孔压边界条件，根据工况的不同，选取不同的孔压边界，同时根据上下游水位的不同，设定初始假定浸润面。

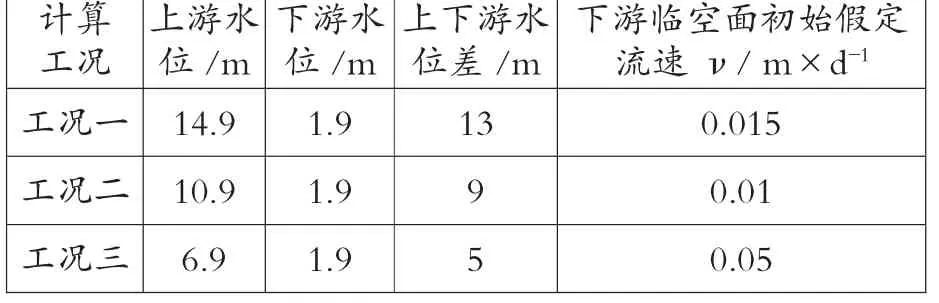
表1 模拟计算工况表

2.3 计算参数

根据勘探资料和室内试验成果，选定了相关计算参数。为节省计算时间，提高有限元收敛速度，考虑不同土层的渗透特性，将土层分为三个大层，其中每一大层的渗透系数值均按每一小层渗透系数值和厚度采用加权平均的方法计算所得。拟选定计算参数如表2。

表2 各土层渗透系数（K）取值表

3 数值模拟结果

3.1 孔隙水压力

工程运行期间，上下游存在水位差，从而发生渗流作用，引起渗流场内孔隙水压力的变化。渗流场内同一垂直面上，孔隙水压力随着深度的增大呈线性增大。由于上下游水位差，渗流场内的同一水平面上，上游河水渗入附近区域的孔隙水压力与下游逸出处的孔隙水压力存在一定的差值。三种工况下该差值大小分别约为127kPa、88kPa及49kPa。

闸址区渗流场内，对于同一高程上的上下游孔隙水压力之差，工况一最大，为13.0～14.0m；工况二次之，工况三最小，为4.0～5.0m。可见，同一高程上的河流上下游水位差越大，渗流场内上下游孔隙水压力之差越大。

3.2 渗流流线

判定渗流场内的渗透稳定性，首先要确定土体的临界水力梯度。根据《水工设计手册》结合该工程土层性质，土体的临界水力比降按照流土计算方法确定。经计算，临界水力梯度Jcr为0.578。当逸出处的水力梯度Je＜Jcr，则土处于稳定状态；当Je=Jcr，则土处于临界状态；当Je＞Jcr，则土处于流土状态。

通过对比可知，同一高程上的上下游水位差越大，在渗透路径长度相同的情况下，渗流逸出处的水力梯度越大。

此次分别计算了三种工况下节制闸附近X=165m、X=-15m、X=115m剖面。总体上看，从上游河水渗入渗流场内土体开始，浸润面坡度逐渐变缓，上游的水力梯度比下游的水力梯度要大，渗流逸出处水力梯度略小于整个剖面上的平均水力梯度。计算中，由于渗流逸出处的水力梯度较难界定，从工程安全角度考虑，取水流在整个剖面上的渗流平均水力梯度作为渗流逸出处水力梯度。综上分析，整个枢纽不存在渗透稳定问题。

3.3 渗流流速

土体内发生渗流时，水力梯度越大，渗流流速越大，流线越密集。由于建筑物两侧土体渗透性大于闸址区底部的土体渗透性，闸底渗流量占总渗流量的比例较小，三种工况下大致相同，仅为7%左右，渗流形式主要为绕闸渗流。在船闸与节制闸之间的分流岛附近，渗流流速较大，流线较为密集。工况一渗流流速最大，流线最密集，工况二次之，工况三最小。工况一分流岛靠近河流上游附近渗流流速最大，为0.523m/d，工况三船闸靠近河流下游附近渗流流速最小，为3.083×10-10m/d。

3.4 渗流流量及渗透压力

为了更直观地反映渗流场内关键区域的渗流稳定性，对关键剖面的渗流流量进行了统计，某剖面的渗流流量，即为该剖面的平均渗流流速与剖面面积的乘积。

通过计算结果可见，三种工况下的渗流流速、渗流流量及渗透压力在渗流场内的分布规律是大体一致的。工况一渗流场内的渗流流速、渗流流量及渗透压力最大，工况二渗流场内的渗流流速约为工况一的68.7%，工况三的渗流场内渗流流速及渗流流量最小，为工况一的37.4%，为工况二的54.4%。渗透压力与水力梯度成正比，水力梯度越大，渗流流速越大，渗流流量越大，渗透压力也就越大。

4 结论

依据工程地质、水文地质条件，通过对该工程渗流稳定性的分析与评价，结论如下：

（1）计算结果符合达西定律的基本规律，水力梯度越大，渗流流速越大，渗流流量也就越大，渗透压力越大。渗流流速在第一种工况下最大，第二种工况下次之，第三种工况下最小。各工况下闸址区渗流场内土体是稳定的，能够满足建筑物结构安全方面的要求。

（2）上下游河水位差越小，下游逸出处的水力梯度越小，土体渗流稳定性就越好；反之亦然。因此，工况三闸址区内渗流稳定性最好，工况二次之，工况一最差。闸址区内的渗流场中，船闸与节制闸间的护堤附近安全系数工况一为3.928，工况二为5.728，工况三为10.509；三个工况下均渗透稳定。

（3）三种工况下船闸和节制闸附近渗流逸出处的水力梯度均小于水力梯度容许值；尽管船闸与节制闸之间的分流岛附近区域及节制闸左右两岸土体附近区域安全系数相对较小，但是仍然满足规范安全系数要求。

（4）该工程渗流方式主要为绕闸渗流，三种工况下绕渗流量所占总渗流量的比例大致相同，约为93%