基于改进CHAN的超宽带定位误差校正算法

金仙力，赵道明

(南京邮电大学 计算机学院，江苏 南京 210023)

0 引 言

在基于物联网的服务中，物体的位置数据是位置相关服务的基本前提。人们在物联网中部署大规模的设备，来感知物联网中关于物体的方方面面的信息，深入挖掘这些信息以总结特征和规律，从而提供给用户相关的业务服务，发挥物联网的经济价值。信息感知是物联网应用的基础[1]。在密集多径环境中实现精确的定位，对于如大型商场、室内停车场等室内环境下的搜索和救援等紧急情况的处理至关重要[2]。利用无线通信技术，感知室内物体的位置，构建室内LBS[3]。现有的短距离无线通信技术中，超宽带以其抗干扰能力强、高达几个GHz的带宽、功耗较小、穿透能力强和良好的保密性等优点，被许多公司用以实现室内实时定位系统(RTLS)。到目前为止，基于超宽带技术的实时定位系统主要有Ubisens的Ubisense RTLS和Zebra Technologies的Dart RTLS等[4]。

利用超宽带技术进行定位的过程无法规避定位误差的出现。这些误差会直接影响定位精度，在一些应急场景中定位误差会导致安全隐患。导致超宽带定位误差产生的主要问题是NLOS(none-line-of-sight)。NLOS问题是指在信号多径传播过程中，没有直射路径，只存在反射和衍射路径，或者检测不到直射路径的情况。与此相反，不经过任何障碍物直线传播到达参考节点称为LOS传播。针对NLOS问题，当前的研究主要包含两类解决方案。一种是NLOS识别，即通过算法判断当前信号属于NLOS传播还是LOS传播。另一种方案是不区分NLOS和LOS，对这些问题采用统一的校正方法进行校正[5-8]。

CHAN[9]是一种基于到达时间差的经典误差校正算法。因其不需要递归即可给出双曲线方程的闭式解，计算简便，在理想高斯噪声环境下精度高等，非常适合在实际工程中应用。相较于视距环境，CHAN算法在非视距环境下的定位性能下降明显[10]。

文中从阐述TDOA算法原理出发，剖析不同分布NLOS误差对CHAN算法性能的影响。先对非视距环境下的TDOA测量值进行分组，再加权平均CHAN算法对各TDOA测量结果集的估计结果以改善CHAN算法的性能，提出CHAN-LCCRW算法。文中将对CHAN算法在视距和非视距环境下的性能进行比较，并通过与CHAN算法和Taylor算法的对比来验证CHAN-LCCRW算法的性能。

1 TDOA定位方法

1.1 TDOA定位原理

出于对TOA算法的改进，TDOA算法不是直接使用信号到达时间来定位，而是用不同基站之间接收到同一目标发来信号的时间差来估算移动台位置。因此，与TOA算法相比，不需要在发送的信号中加入专门的时间戳，定位精度相对较高。信号的到达时间差的获取，实际应用中最常用的方式是利用相关性运算的方法[11]。这种算法可以在基站和移动台不同步时，估算出TDOA的值。由于做到基站与移动台的同步十分复杂，所以借助相关估计产生TDOA测量值，而后利用定位算法得出估计坐标的方法的应用最为广泛。

对于任意一个TDOA值，实际上表示的是来自移动台的脉冲信号到达两个基站的时间的差值。由于信号在空气中传输的速率接近光速，故用TDOA值与光速的乘积可以表示移动台到两个基站之间的距离差为定值，满足双曲线方程的形式。两组双曲线方程联立即可得到可行解。

1.2 TDOA定位模型

如果在一个二维空间内采用TDOA定位，那么为了得到空间中位置为[x,y]T的移动台的坐标，至少需要三台定位基站参与定位。空间内共有N(N≥3)个基站参与了移动台的定位，假设每个基站的坐标分别为Pi=[xi,yi]T,i=1,2,…,N。为了方便应用，通常以一个基站的信号为基准，将其余基站的信号与之进行相关运算来产生TDOA值，假设为基站1。用ti,1表示基站i与基站1之间的信号到达时间差，di表示基站i到移动台的距离，di,1表示基站i与基站1到移动台的距离之差，则有下式：

di,1=cti,1=di-d1,i=1,2,…,N

(1)

另根据二维空间的欧氏距离公式有：

x2+y2,i=1,2,…,N

(2)

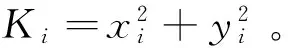
将式(1)带入式(2)得：

(3)

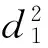
(4)

其中，xi,1=xi-x1表示基站i与基站1横坐标的差值；yi,1=yi-y1表示基站i与基站1纵坐标的差值。显然，式(4)是关于未知数x,y和d1的线性方程。

2 CHAN-LCCRW定位误差校正算法

2.1 CHAN算法

CHAN算法对于移动台的估计位置的解法分为两种情况：

(1)只有三个基站接收到目标信号。

当系统中只有三个基站接收到移动台的脉冲信号，即i=2和i=3时，将式(4)组成矩阵方程然后求解可得：

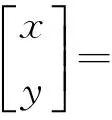
(5)

将式(5)带入式(2)可以得到关于d1的两个候选解，根据可行域限制排除掉一个解后，可以得到d1的解，带入式(5)得到估计坐标。

(2)存在四个或更多基站接收到目标信号。

当存在四个及以上基站接收到移动台的脉冲信号时，令za=[x,y,d1]T。首先假设za的各元素之间相互独立，那么其最大似然估计为：

za=argmin{(h-Gaza)TΨ-1(h-Gaza)}=

(6)

其中，

式(6)可以近似表示为：

(7)

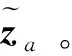
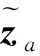
(8)

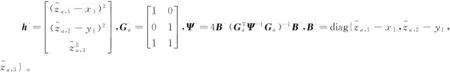
(9)

2.2 CHAN-LCCRW算法的主要思想

文中提出的CHAN-LCCRW误差校正算法，根据超宽带定位系统产生的多组TDOA测量值，通过CHAN算法得到校正过系统误差的初步估计坐标，再采用残差加权的方式来抑制NLOS误差对定位结果的影响。

残差是用来描述一个定位估计结果与一组TDOA测量之间的接近程度，通常在NLOS误差是系统的主要误差来源时，一组TDOA测量中受到NLOS影响越大，其计算出的残差值越大[12]。残差值还受到一组测量元素个数的影响，因此文中采用标准化残差来衡量一组TDOA测量受到NLOS的影响。标准化残差是指残差的平方和除以该组的元素个数，定义如下：

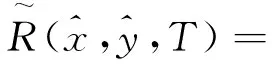
(10)

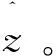
为了减小计算量以提高系统的实时性，对残差加权算法进行了改进，采取一种低计算量的残差加权方法[13]。当系统中有很多基站接收到来自移动台的信号时，能够大幅减少计算数。其与传统残差加权的计算估计坐标次数对比如表1所示。

表1 两种算法估计坐标的计算次数对比

以在二维空间为例，假设共有M个基站接收到来自移动台的信号。CHAN-LCCRW算法的步骤描述如下：

Step1:处理M个基站检测到的待测目标信号。以某一基站为参考站，通过相关运算产生了M-1个TDOA测量值。

Step2:如果M=3，跳转到Step8；如果M>3，跳转到Step3；否则测量不足，结束。

Step4:假设Smin中共有P个元素，分别将第i个元素从Smin中移除，共产生P个包含P-1个元素的测量值的组合，记作Ctemp={S1,S2,…,SP}。

Step5:如果P大于3，跳转到Step6；否则，跳转到Step7。

Step8:将候选集Sc中所有的坐标和对应的标准化残差值的倒数按式(11)相乘再求和后除以标准化残差的倒数和，最后得到移动台的估计坐标。

2.3 CHAN-LCCRW算法的流程图

根据CHAN-LCCRW算法的步骤，绘制该算法的流程图，如图1所示。

图1 CHAN-LCCRW算法流程图

3 仿真与分析

3.1 实验设置

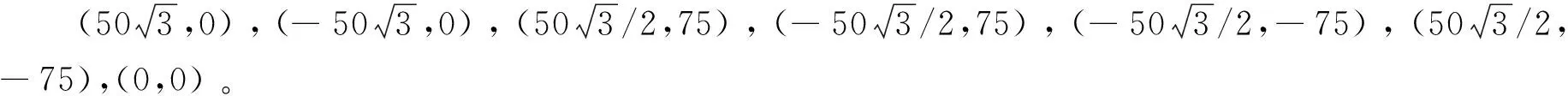
寻找合适的评价指标来表示出定位的精度对于定位误差校正算法的性能分析至关重要。在现有的研究中，广泛采用误差累积分布函数和均方根误差来衡量一个定位方法的定位精度和一种误差校正算法的性能。均方根误差(root mean square error，RMSE)是指在有限次的测量中，将每次测量值与对应的真实值误差的平方值求和后，再取平均值，最后求平方根后的结果。累积分布函数(cumulative distribution function，CDF)给出与某个分布相关联的累积概率。累计分布函数可以给出误差低于特定值的概率，所以其在实际工程应用中常用于描述定位系统的精度范围。

3.2 仿真结果分析

图2中给出了在视距以及非视距环境下CHAN算法定位性能与参与定位的基站数的关系。结果表明，随着接收到目标信号的基站数的增加，CHAN算法的RMSE不断降低。这是由于基站数的增加可以提供更多的冗余TDOA测量值，使得CHAN算法的结果更加准确。在NLOS误差分别服从高斯分布、瑞利分布和指数分布时，CHAN算法定位的RMSE值均远大于LOS环境下的RMSE值，在参与定位的基站数较少时，定位误差由厘米级增加到米级。

图2 不同环境下CHAN算法的定位性能

克拉美罗下界(Cramér-Rao low bound，CRLB)是对于参数估计问题提出的，为所有无偏估计量的方差提供了一个下限。图3为NLOS误差满足不同均值的指数分布时，对CHAN算法、Taylor算法和CHAN-LCCRW算法的均方根误差情况进行仿真的结果，并与克拉美罗下界进行比较。在NLOS误差较小时，三种算法的定位性能相当。随着NLOS误差的增大，CHAN-LCCRW算法的定位性能与CHAN算法相比优势较大，体现了对NLOS误差较好的抑制作用。文中算法具有与Taylor算法较为接近的均方根误差值，但较Taylor算法解决了初值难以选取和需要迭代计算的问题。

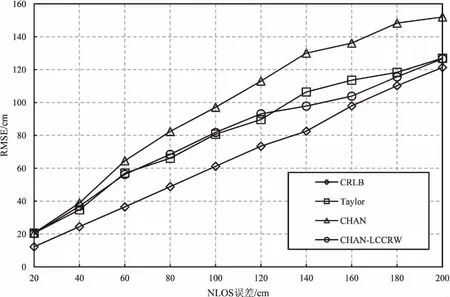
图3 不同NLOS误差下各算法的定位性能

图4展示了在NLOS误差服从均值为2m的指数分布时，各算法的定位误差的累计分布函数。CHAN-LCCRW算法有约50%的概率将定位误差控制在1m以内，而对于Taylor算法和CHAN算法，其概率分别为40%和30%。定位误差小于2m时，表明NLOS误差受到了抑制。CHAN-LCCRW算法有效抑制NLOS误差的概率为97%左右，超过Taylor算法和CHAN算法10%以上。综上所述，CHAN-LCCRW算法具有较高的定位精度，适合应用到实际工程。

图4 各算法的累积分布函数

4 结束语

定位精度一直是基于超宽带的室内定位系统的关键性能属性，提高定位精度的主要手段就是对定位误差进行校正。为了进一步提高非视距环境下CHAN算法的精度，分析了不同分布的NLOS误差使CHAN算法精度衰退的程度。利用残差加权的思想对CHAN算法进行改进，提出了CHAN-LCCRW算法，对误差实施了校正，最后应用Matlab完成该算法的仿真实验。结果表明，CHAN-LCCRW算法有效抑制了NLOS误差，提高了CHAN算法在非视距环境下的定位精度。

[1] 胡永利,孙艳丰,尹宝才.物联网信息感知与交互技术[J].计算机学报,2012,35(6):1147-1163.

[2] GEZICI S,TIAN Z, GIANNAKIS G B,et al. Localization via ultra-wideband radios:a look at positioning aspects for future sensor networks[J].IEEE Signal Processing Magazine,2005,22(4):70-84.

[3] 周傲英,杨 彬,金澈清,等.基于位置的服务:架构与进展[J].计算机学报,2011,34(7):1155-1171.

[4] 班 贺.基于RFID技术的仓储管理系统研究与应用[D].南京:南京理工大学,2015.

[5] KHODJAEV J，PARK Y，MALIK A S.Survey of NLOS identification and error mitigation problems in UWB-based positioning algorithms for dense environments[J].Annals of Telecommunications,2010,65(5):301-311.

[6] 贺远华,黎洪生.无线传感器网络节点的非视距定位方案研究[J].计算机工程与应用,2010,46(25):82-84.

[7] BARTOLETTI S,GIORGETTI A,WIN M Z,et al.Blind selection of representative observations for sensor radar networks[J].IEEE Transactions on Vehicular Technology,2015,64(4):1388-1400.

[8] 吴绍华, 张钦宇,张乃通. 密集多径环境下UWB测距的NLOS误差减小方法[J].电子学报,2008,36(1):39-45.

[9] CHAN Y T,HO K C.A simple and efficient estimator for hyperbolic location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915.

[10] 陆 音,王宝全,丘觐玮.CHAN算法在LOS和NLOS环境下的定位研究[J].计算机技术与发展,2015,25(9):61-65.

[11] CARTER G C.Coherence and time delay estimation[J].Proceedings of IEEE,1987,75(2):236-255.

[12] CHEN P C.A non-line-of-sight error mitigation algorithm in location estimation[C]//Wireless communications and networking conference.[s.l.]:[s.n.],1999:316-320.

[13] JIAO L,XING J,ZHANG X,et al.LCC-Rwgh:a NLOS error mitigation algorithm for localization in wireless sensor network[C]//International conference on control and automation.[s.l.]:IEEE,2007:1354-1359.

[14] BING L,WEI C,BIN W.A robust wireless sensor network localization algorithm in mixed LOS/NLOS scenario[J].Sensors,2015,15(9):23536-23553.

[15] 郑 飞,郑继禹.基于TDOA的CHAN算法在UWB系统LOS和NLOS环境中的应用研究[J].电子技术应用,2007,33(11):110-113.

[16] 王建辉,崔维嘉,胡捍英.基于神经网络的鲁棒NLOS误差抑制算法[J].计算机工程,2011,37(24):7-9.

[17] 肖 竹,谭光华,李仁发,等.无线传感器网络中基于超宽带的TOA/AOA联合定位研究[J].计算机研究与发展,2013,50(3):453-460.