基于CFD的DTMB船舶艏部型线优化研究
2018-03-20蔡寒冰冯佰威常海超
蔡寒冰,冯佰威,常海超
(1.武汉理工大学 交通学院,湖北 武汉 430063;2. 武汉理工大学 高性能船舶技术教育部重点实验室,湖北 武汉 430063)
0 引言
船体型线设计是船舶总体设计中的核心环节,型线设计的优劣对船舶综合航行性能具有重要影响。随着计算机技术的发展,计算流体力学(Computational Fluid Dynamics,CFD)在理论研究上不断取得突破,已经越来越多地被应用于船舶型线优化设计。船型优化采用CFD技术,可以减少模型试验次数和船舶设计的时间,提高船舶设计的效率[1]。ZHAO Yong等[2]对Wigley船型进行优化,使其兴波阻力降低了49.6%。
一套完整的船型优化工具一般由船型变换模块、CFD计算模块以及优化模块[3]组成。船型变换模块用于模拟实船船型并对它进行变形;CFD计算模块用于计算流场和评估目标函数;优化模块则是通过优化算法对优化设计中选定的优化变量进行优化,最终达到优化船型的目的。
在船型优化工具中,船型变换模块决定了船型优化设计空间的大小,是船型优化工具的关键模块。目前,船型变换模块采用的船体曲面变形技术多是基于NURBS(Non-Uniform Rational B-Spline ,非均匀有理B样条)原理对船体曲面进行变形。融合方法是以多条母型船为基础,通过调整融合参数将其进行内插来生成新船型的技术。冯佰威等[4]使用融合方法修改母型船的NURBS控制点,再由得到的控制点生成新的船型曲面,通过这种方法对1 300标准箱集装箱船艏部进行了优化。自由变形技术则是建立一个由三维控制点构成的长方体框架,将待变形物体嵌入到框架中,通过移动控制顶点来实现船体变形。TAHARA Y等[5]运用该方法对DTMB 5415船型进行了优化和性能分析。
径向基插值技术(Radial Basis Function,RBF)在船型优化领域也得到了应用。沈通等[6-7]选择船体NURBS曲面的控制点为设计变量,通过改变这些变量的值来实现对船体曲面的变形。在实际应用的过程中,通过控制点来对船体曲面进行变形有诸多不便。因此,本文提出了一种基于船体曲面型值点的曲面变形方法,并以该方法为基础开发了船型变换模块,使用CFD-shipflow软件对新生成的船型进行评估,最后使用遗传算法对船型进行筛选,对DTMB 5415船型进行了减阻优化设计。
1 船体曲面修改方法
1.1 基于径向基函数的船体曲面插值
径向基函数是一种沿径向对称的标量函数,是空间中任一点X到某一中心Xi之间欧氏距离║X-Xi║的函数[8-9]。当其应用于船体曲面修改时,采用如下形式[10]:
(1)
式中:S(X)为点X=(x,y,z)在船体曲面上移动的距离;λi为基函数的权重系数;p(x)为仿射变化的低阶多项式,其中,p(x)=c1x+c2y+c3z+c4;n为控制点个数;‖X-Xi‖为两点之间的欧氏距离;Φ为
给定的基函数,这里使用具有紧支性的Wedndland′s函数的三维形式:
(2)
方程中的系数λi、ci由下述方程计算得到:
S(X)=fi,i=1,2,…,n
(3)
式中:fi为点的变化量。
同时,为了保证方程有解,权重系数λi应满足下述约束条件:
(4)
将式(3)与式(4)联立,可得如下矩阵:
(5)
将数据带入式(5),就可以反解得到λi、ci,将得到的参数带入到式(1),就可以得到所有需要点的新坐标,最终得到新的曲面。
在实际的船体曲面变形应用中,需要选取两种类型的点。一种类型的点是约束点(fi=0),这种点的位置在优化过程中保持不变,选取它们的目的是为了在优化过程中约束住船体曲面的基本形状保持不变,并保证船型在优化完成后能够满足约束条件。一般在船型优化问题中,选取船体的轮廓线,例如甲板边线、船底线、靠近平行中体部分的横剖线上的点作为约束点。另一种类型的点是优化点(fi≠0),这种点可以看成是优化过程中的优化变量,通过使用优化算法改变这些优化点的位置,使得优化问题的目标函数达到最小。
1.2 基于型值点的曲面变形
目前,将RBF运用到船型优化领域中的研究[3,6-7,10-12],多是选择船型NURBS曲面的控制点作为约束点和优化点,通过修改这些控制点来达到对船体曲面变形的目的,见图1。该方法的选点过程见文献[6-7,10-12],一般是读取船体曲面的iges(Initial Graphics Exchange Specification,基本图形交换规范)文件中船体曲面的控制点数据,并根据优化的实际需要从控制点中选择约束点和优化点,从而实现船型的自动变形。

图1 基于NURBS控制顶点的曲面变形
在图1中,正方形点为约束点,圆形点为优化点,这两种点都是在船体NURBS曲面的控制网格上选取的,并非船体曲面的型值点。
在实际的船型优化应用中,基于曲面控制点的RBF变形方法有一些不足之处:
(1)控制点只具有数学含义,而不具备物理含义。在进行船型分析时,不能根据控制点的变化量准确地分析出船型曲面的变化。
(2)由于控制点的位置并不是船体曲面实际型值点的位置,在优化过程中会出现某条需要约束的水线或横剖线发生变形的情况。
针对以上不足,本文提出了基于型值点的船体曲面变形方法。相比于使用控制点,型值点更具有实际的物理意义,根据型值点变化量可以分析出船型曲面的变化;同时,由于型值点反映了曲面在该点处的实际位置,故对型值点进行约束不会出现该点处的剖面发生变形的情况。本文使用基于型值点的RBF变形方法对DTMB 5415船型的球鼻艏部分进行变形,以验证该方法的合理性和实用性。
DTMB 5415船型三维模型见图2,主要尺度要素见表1。

图2 DTMB 5415模型
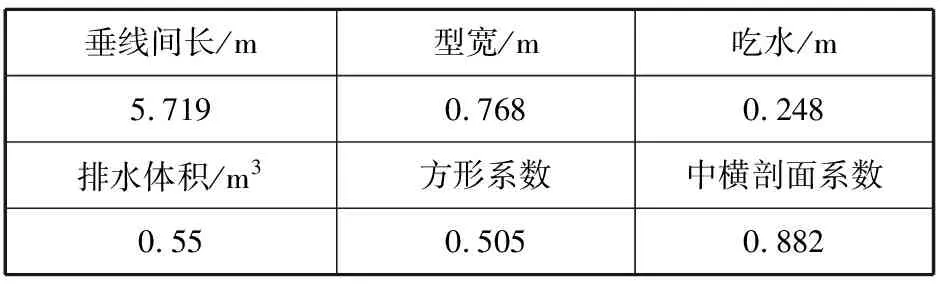
表1 DTMB 5415船模主要尺度要素
首先,将船体曲面离散为空间点云,见图3。其次,选择甲板边线、船底线以及一部分艏柱线上的型值点作为约束点,约束住这部分的变形,使其保持不变。最后,在球鼻艏处选择了3个型值点作为优化点,其中,型值点1沿X轴和Z轴变化,型值点2沿Y轴变化,型值点3沿Z轴变化。通过改变这三个型值点的坐标,可以达到改变球鼻艏形状的目的。

图3 艏部优化点与约束点位置
将所选择的型值点坐标值,包括优化点和约束点的坐标值带入到式(5)中,就可以反解得到所有的未知系数λi、ci,再将剩余的型值点数据带入到式(1)中,就可以得到所有待求型值点的数据,最后根据这些型值点就可以反算出新船型的NURBS曲面,得到新的船型。
母型船与改变船的船型对比见图4,其中,实线为母型船型线,虚线为变形船型线,点划线为约束住的船体外轮廓。
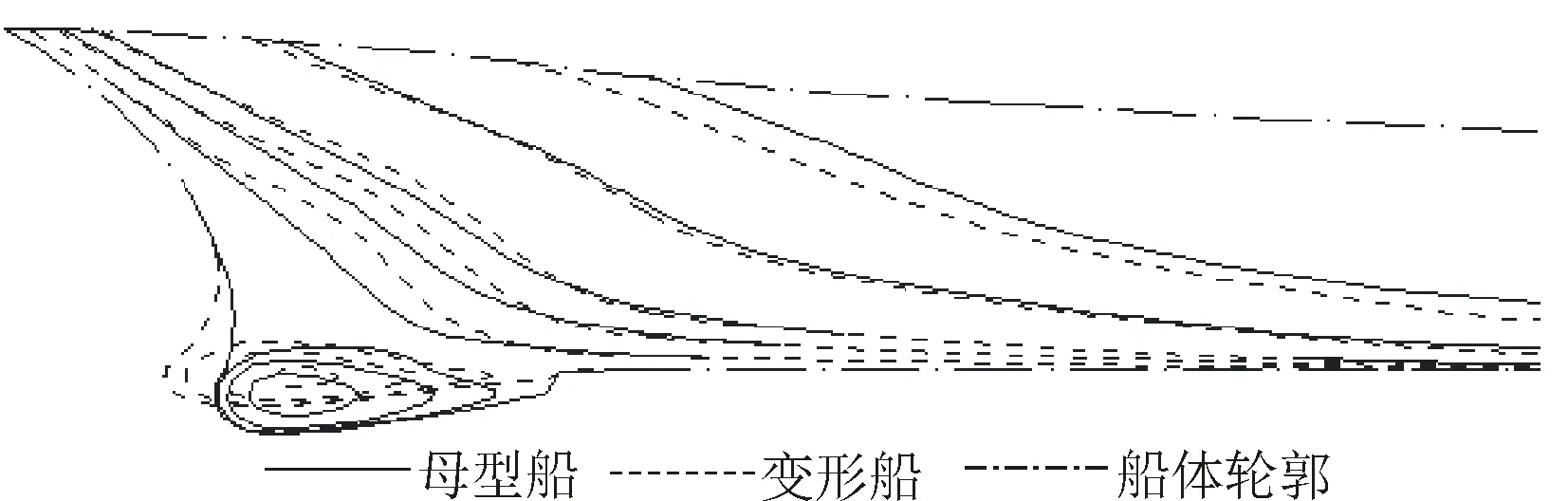
图4 变形前后的船型艏部对比
图4显示,变形后,整个球鼻艏的形状有了明显的改变;作为约束变量的甲板边线、船底线以及部分艏柱线的位置并没有发生改变;改变后的船型型线光顺性良好,这说明基于曲面型值点的RBF曲面变形方法可以满足船型优化的需要。
2 DTMB 5415艏部型线优化
2.1 优化目标及约束条件
本文希望在一定的航速下,优化的船型能通过减小船舶的兴波阻力从而达到减阻的效果。因此,本文的优化目标定义如下:
minfobj=Cw,Fr=0.28
式中:fobj为目标函数;Cw为兴波阻力系数;Fr为傅汝德数。
本文的约束条件为:
(1)静水力约束:
Δ-Δopti≥0
式中:Δ为母型船排水量;Δopti为优化船排水量。
(2)型线约束:仅改变艏部线型的几何形状,船宽B、吃水T、艉部线型保持不变。
2.2 优化变量
本文在艏部选取了8个型值点作为优化变量,见图5。
为了控制球鼻艏的形状,使球鼻艏的形状能向有利于兴波阻力的方向变化,型值点1和点4沿X方向(船长方向)、Z方向(吃水方向)变化;而其余型值点则只沿Y方向(船宽方向)变化。
如图5所示,本文选取中纵剖面以及横剖面上的点作为约束点,确保在优化变形过程中,船体基本形状保持不变的同时,船的排水量等数据不会发生较大的改变。
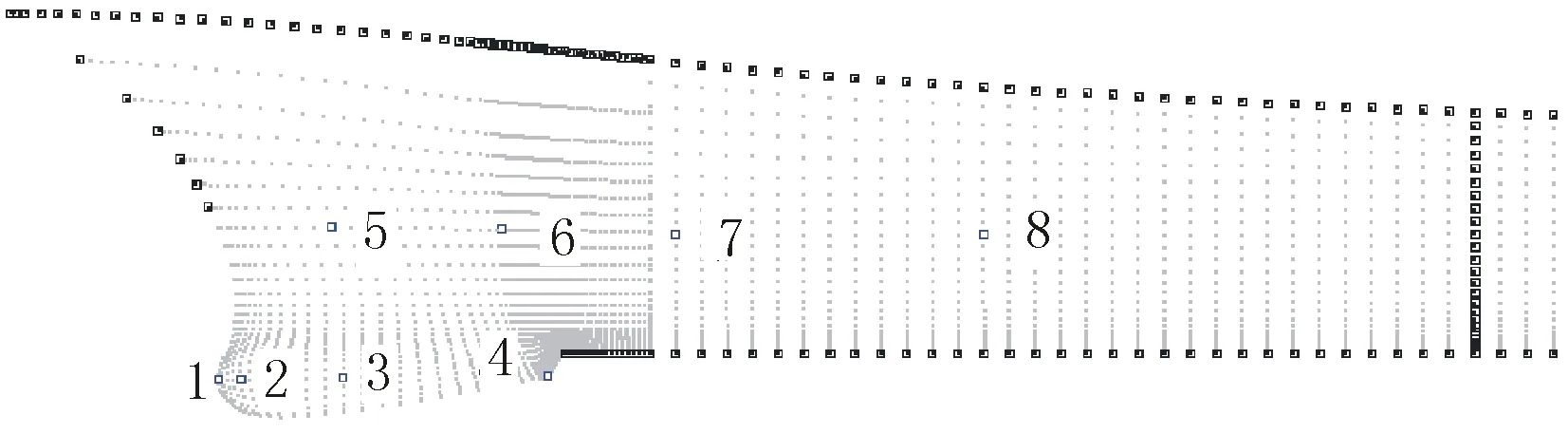
图5 艏部优化变量的选取
选定了优化点与约束点后,其他型值点的求解过程如1.2节所述,此处不再赘述。
2.3 优化流程
本文的船型优化流程见图6,具体阐述如下:
(1)分析母型船并读取型值点。
(2)在型值点中选择约束点和优化点。
(3)运用径向基函数插值技术进行船艏部曲面的变形。
(4)对新生成的船型进行兴波阻力计算。
(5)采用遗传算法进行船型优化,若达到遗传次数则输出优化的船型,反之则修改优化变量,重复上述过程。
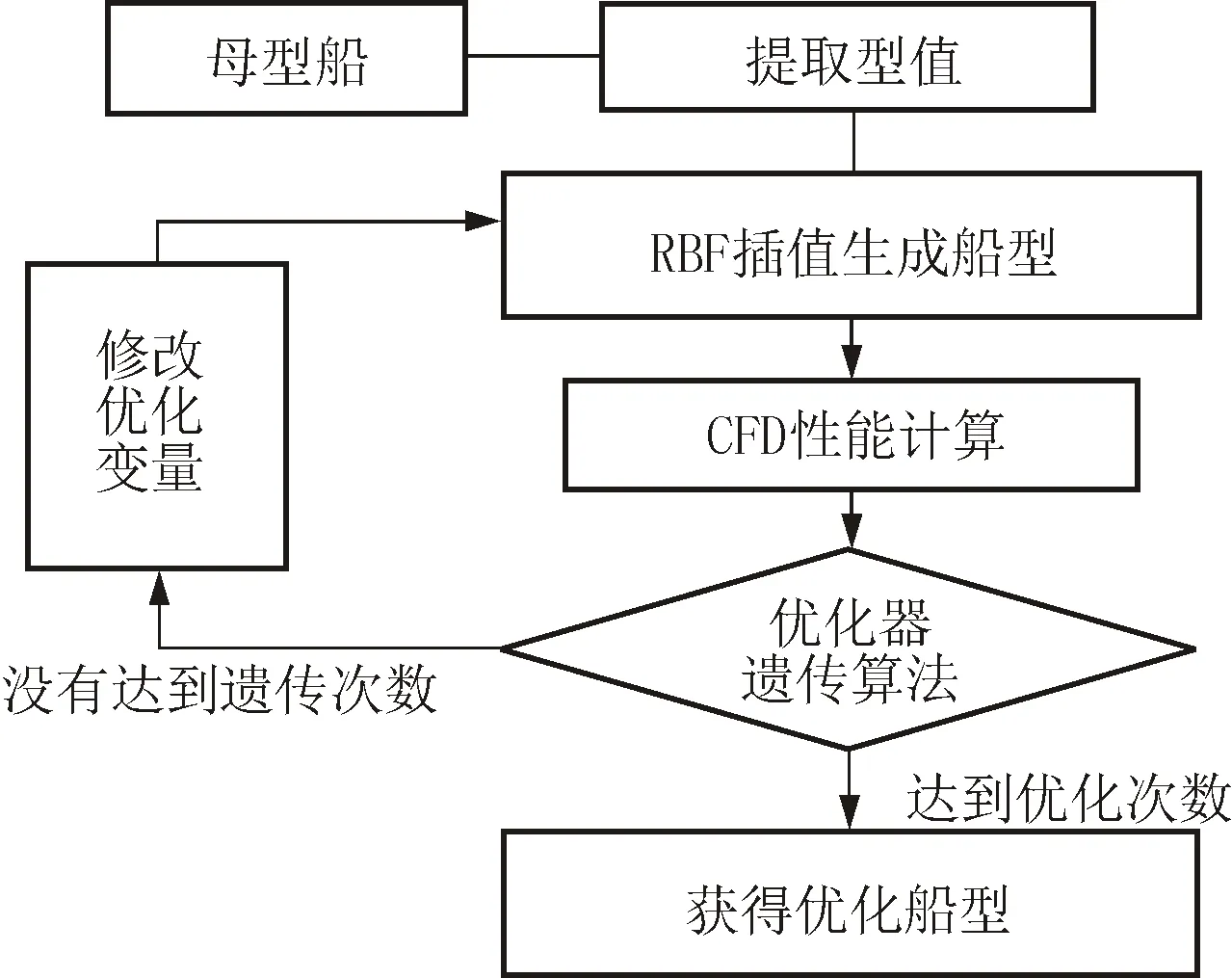
图6 船型优化流程
2.4 优化结果及分析
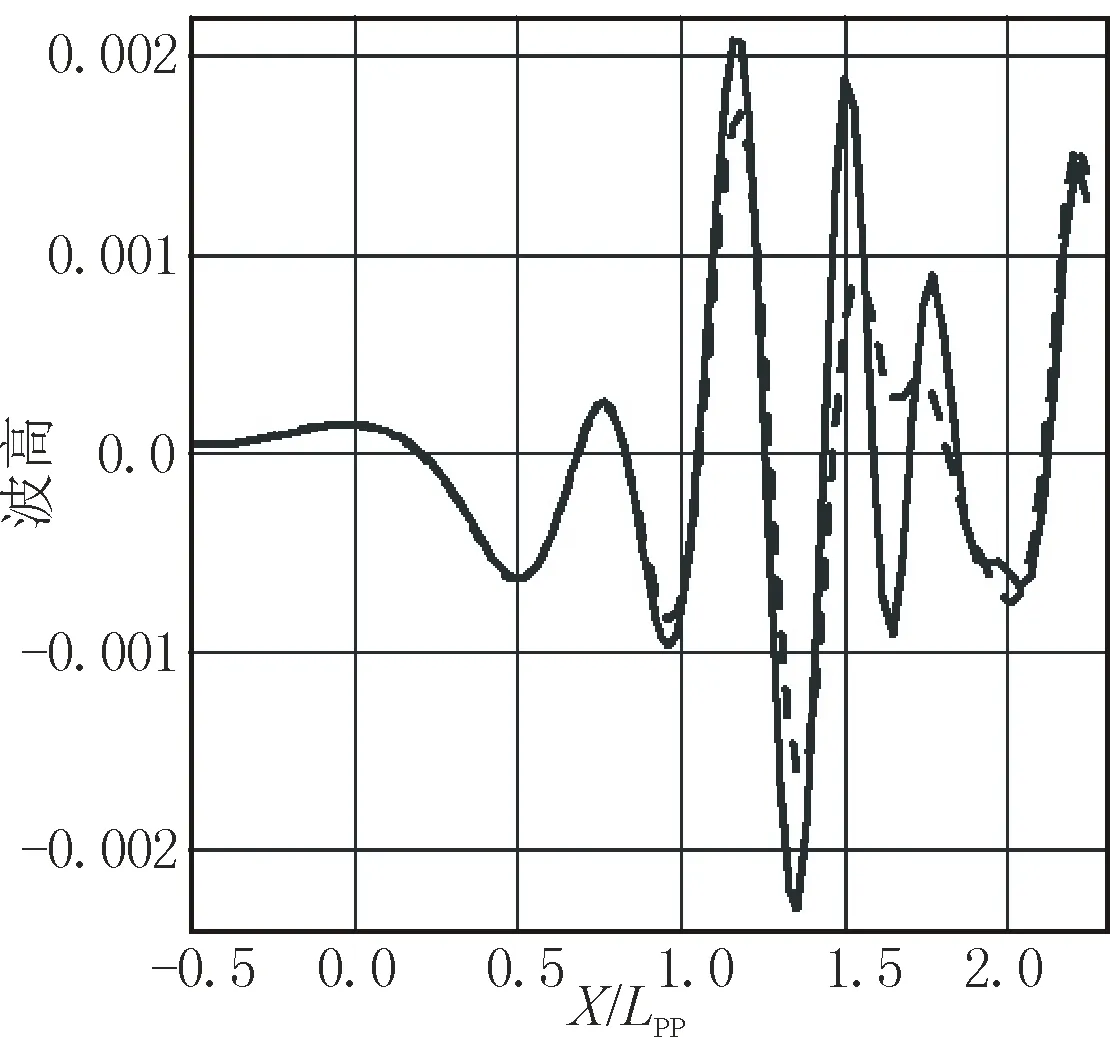
母型船与优化船性能指标的对比见表2,型线对比见图7、图8,波形图见图9,波切图见图10。图10中,X、Y为船体坐标系坐标值。
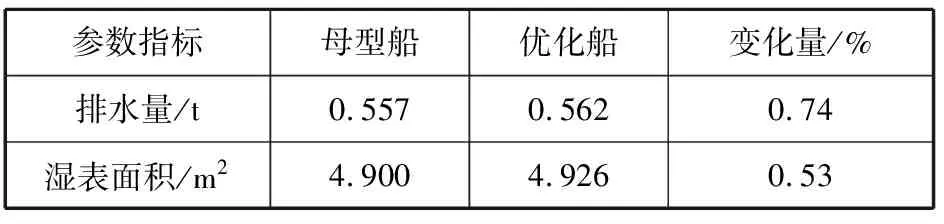
表2 母型船与优化船性能指标的对比
从表2可知,与母型船相比,优化船的排水量、湿表面积都略有增大。另外,经过CDF计算,与母型船相比,优化船兴波阻力RW下降了19.57%。
图7、图8显示,与母型船相比,优化船的整个船型在设计水线处,艏部变得较瘦,平行中体部分变得更为丰满,水线处的进流角减小,这种线型对改善兴波阻力有利;同时优化船球鼻艏向前方延伸,整个球鼻艏变成了前后较瘦、中部较肥的形状,球鼻艏与主船体形成了有利干扰,可以降低兴波阻力。图9和图10显示,优化船的波形数有所减少,船艏附近的波形切片的幅值也有所降低。结果说明优化船的兴波阻力性能得到明显的改善,同时也印证了前文船型变化对兴波阻力性能影响的分析是正确的。

图7 母型船与优化船纵剖线对比
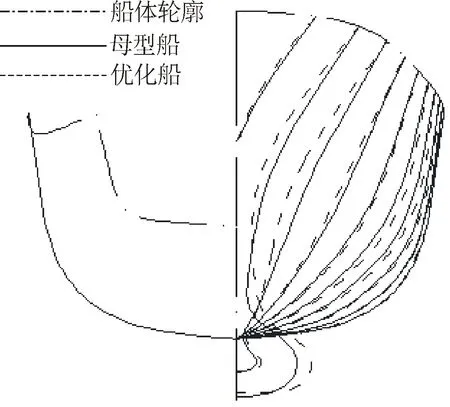
图8 母型船与优化船横剖线对比
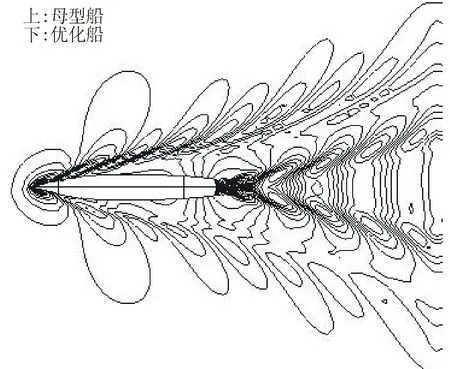
图9 波形图对比
实线:母型船;虚线:优化船
3 结论
为实现基于CFD的船型优化设计,本文提出了一种基于型值点的船体曲面变形方法,并验证了该方法的实用性,最后将其运用船型优化中。
(1)基于型值点的船体曲面变形方法不仅能保证船体曲面的光顺性,而且使局部变形更为灵活,拓展了船型变化的空间。
(2)基于型值点的船体曲面变形方法弥补了控制点的不足,使得RBF方法更能适应船型优化的需要,同时也更有利于船型分析。
(3)通过将CFD数值计算和优化算法的寻优机制相结合来驱动型值点坐标发生变化,得到了满足目标函数的最优船型,实现了船型的仿真优化设计。
(4)船型优化平台能够满足初期型线设计的需要,具有一定的工程应用价值。
