石墨板多孔电极模型构建快速反应区的研究
2018-03-19张琦陈天佐
张琦,陈天佐
(工业和信息化部电子第五研究所华东分所,江苏 苏州 215011)
0 引言
目前,液相储能体系的最理想电极当属多孔结构的碳电极。本论文以石墨板构建多孔电极模型及快速反应区,将电能储存于多孔碳电极表面液层中具有电化学活性的化学物质中,作为电化学储能方式,充放电过程是实现液相中活性物质的化学能与电能之间相互转换的过程。该过程不涉及固相反应以及固相间的离子传输过程,比能量的大小与活性物质的总量有关。
1 多孔电极模型的构建
采用激光雕刻加工技术,将石墨板电极加工为多孔电极。在1.2 cm×6 cm×1 mm的石墨板电极一侧制作出孔径为20~30 μm的100×100多孔阵列,孔中心距离为100 μm,孔深度为80 μm,多孔电极表观面积为10 mm×10 mm,如图1-2所示。控制激光雕刻参数可得到反应距离可控的反应区。

图1 填充活性物质的石墨板多孔电极图片

图2 石墨板多孔电极OM图
2 反应区的电化学过程
以上述石墨板多孔电极为工作电极,纤维碳毡为对电极,饱和甘汞电极为参比电极,阴离子交换膜为隔膜,组成模拟电池,进行充放电实验。正极活性物质为2.0 M VOSO4,负极活性物质为1.0 M V2(SO4)3,电解液均为2 M H2SO4溶液,并保持负极活性物质的量始终大于正极活性物质的量,不影响模拟电池中工作电极的测试。在石墨板多孔电极的充放电性能实验中,工作电极充放电电位范围控制在0.6~1.0 V之间,从1~40 mA·cm-2逐渐地增大充放电的电流密度,相应的充放电时间从450~7.35 s逐渐地减小。通过比较不同的充放电时间 (即不同的电流密度),研究充放电平台的变化情况和充放电容量的倍率性能。
石墨板多孔电极的充放电性能如表1所示。从表1中可以看出,这种以上述石墨板多孔电极为工作电极进行的电化学反应,在一定的电位范围内,随着充放电电流密度的逐渐增大,充电容量有所降低,放电容量也有所降低,但它们衰减的趋势与其他工作电极的电化学反应相比更为缓慢,表现出该电极优异的倍率性能。石墨板多孔电极的充放电性能曲线如图3所示,充放电倍率性能曲线如图4所示。从图3-4中可以看出,在不同大小的充放电电流密度情况下,增加60多倍充放电倍率,此电化学体系仍体现出明显的充放电电位平台,充分地证明了扩散导致的电化学极化不是明显的控制步骤,基于此提供了快速电化学储能的基础。490 C倍率下的容量保持率为8 C倍率的67%,具有优异的倍率性能。

表1 石墨板多孔电极的充放电性能
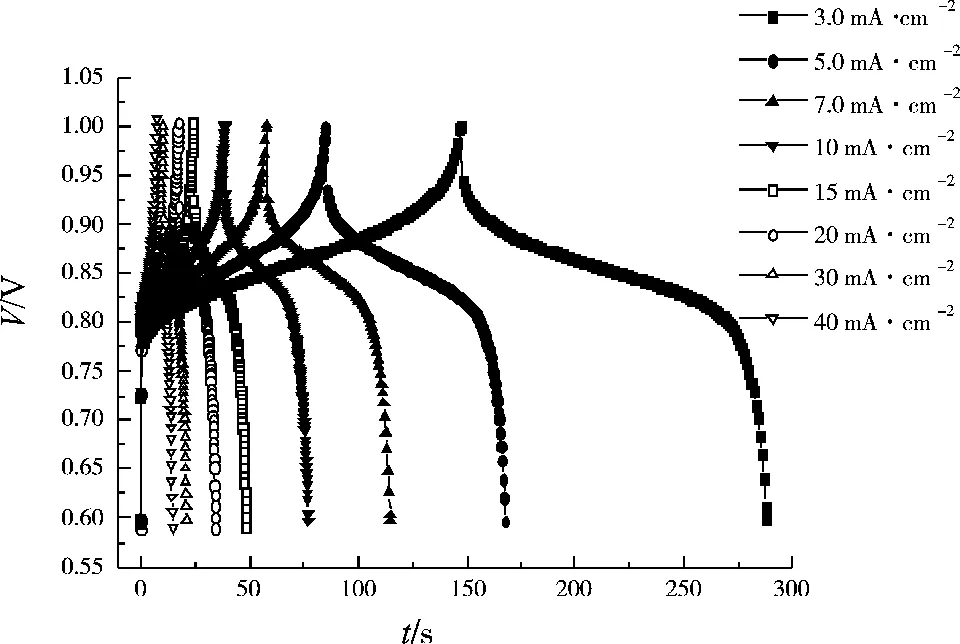
图3 石墨板多孔电极的充放电性能曲线

图4 石墨板多孔电极的充放电倍率性能曲线
3 反应区传质过程的机理分析 [1-5]
使用平板电极,在静止的均相溶液中有物种O,参考一般反应O+ne→R。假设初始溶液中只存在物种O,电极动力学无论快慢,都可以通过足够负的电势活化反应,在电极表面让物种O被完全还原,使得物种O的表面浓度为零。
扩散方程可以根据适当的边界条件来求解。
Fick第二定律:

根据初始化条件,在实验开始前t=0,溶液是均匀的;半无限条件t→∞保证了实验过程中,远离电极的本体相保持不变;发生电化学氧化还原反应后电极表面氧化态物质O的表面浓度为零。
对于物质O,经过Laplace变化后,上式可以变换为柯泰尔方程 (Cottrell equation):
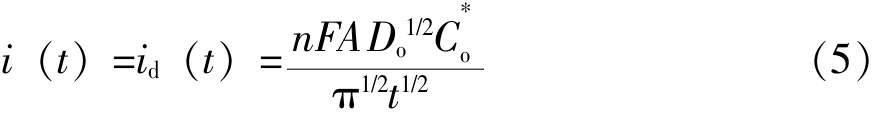
式 (5)中:i—— 电流,单位为A;
id——扩散极限电流,单位为A;
n——电极反应过程中涉及的电子数;
F——法拉第常数,值约为964 85 C·mol-1;
A——电极面积,单位为cm2;
Do——电解液的扩散系数,单位为cm2·s-1;
Co*——电解液的本体浓度,单位为mol·cm-3;
t——时间,单位为s。
Cottrell方程表示电极附近的电化学活性物质产生的电流i与t-1/2存在线性关系,扩散系数可以根据线性拟合直线的斜率计算得到。
如果记录的响应是电量对时间的函数Q(t),则Cottrell方程也可以从t=0开始对电流进行积分。
Fred Anson方程:
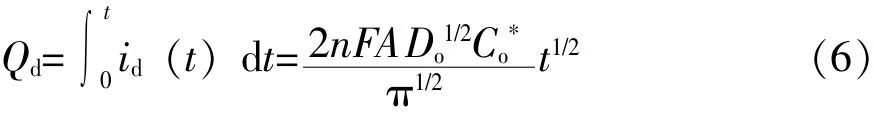
Fred Anson方程中,Qd与t1/2存在线性关系。在实际电量中,存在双层充电Qdl,导致Q对t1/2的直线一般情况下是不通过原点的。
在标准电流阶跃法测试中,2.0 M VOSO4溶液中 VOSO4的扩散系数 Do为 1.15×10-6cm2·s-1。 针对上述实验结果,处理反应区的电化学性能数据,如图5所示,将电流密度对放电时间作图,得到电流密度-放电时间-0.5曲线。根据Cottrell方程计算得出2.0 M VOSO4溶液中VOSO4的扩散系数Do为1.27×10-6cm2·s-1。将电流密度对放电容量作图,得到电流密度-放电容量-1曲线,如图6所示。根据Fred Anson方程计算得出VOSO4的扩散系数Do为1.49×10-6cm2·s-1。 计算所得的扩散系数 Do与标准电流阶跃法测试的数据基本相同,说明石墨板多孔电极所构建的电化学反应基本由扩散作为主导控制。
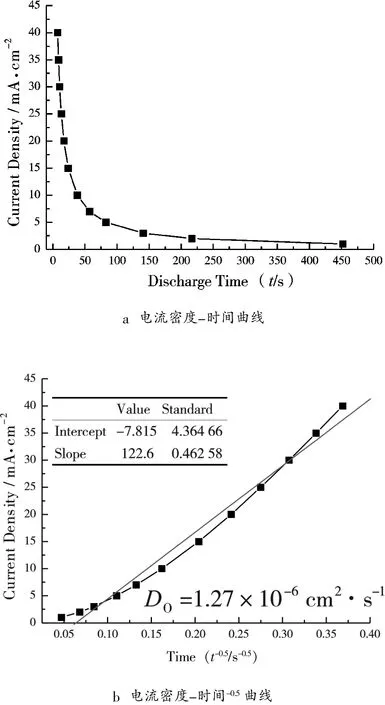
图5 电流密度-时间曲线图
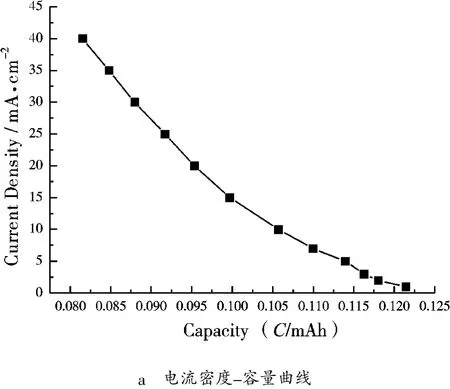
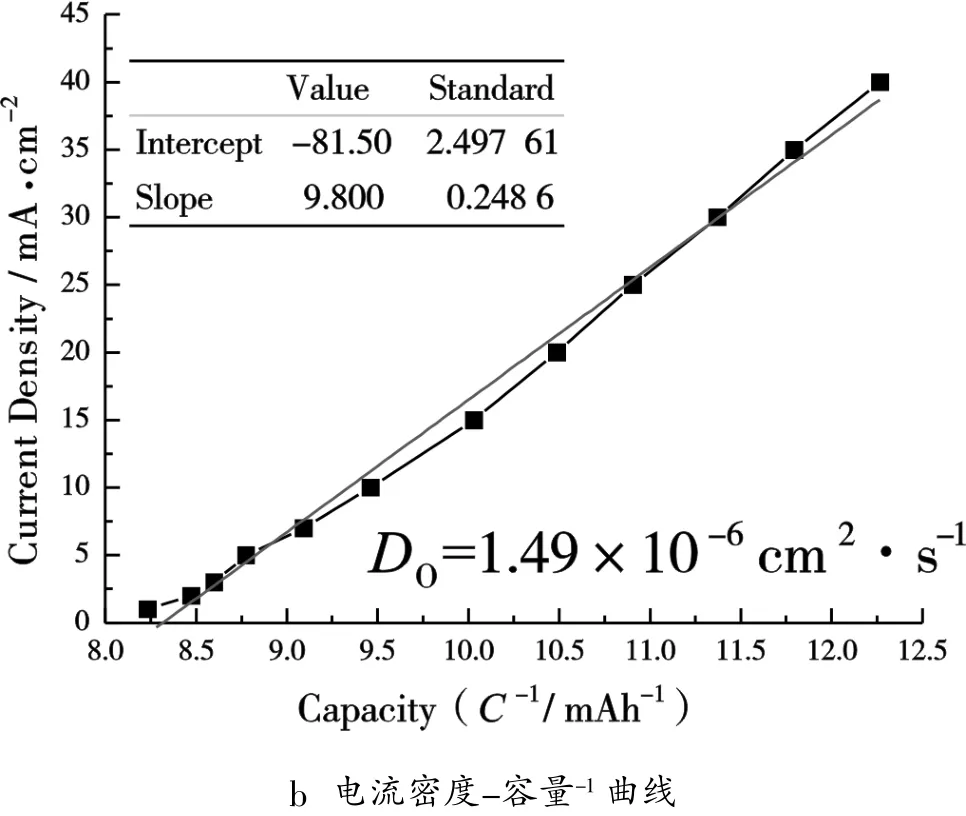
图6 电流密度-容量曲线图
4 结束语
本文以石墨板电极构建了多孔电极模型和快速反应区,探讨了多孔电极模型用于电化学反应的快速充放电能力和倍率性能,在充放电过程中实现了液相中活性物质的化学能与电能之间的相互转换。
采用石墨板多孔阵列电极作为工作电极来构建电化学反应区,由于扩散速率的提高,获得了较高的倍率性能。在490 C的高倍率下,容量保持率为8 C倍率的67%,并且该储能体系仍然能够保持稳定的充放电平台,为实现快速电化学储能提供了基础。
[1]田昭武.电化学研究方法 [M].北京:科学出版社,1984.
[2]陈体衔.实验电化学 [M].厦门:厦门大学出版社,1993.
[3]查全性.电极过程动力学导论 (第三版) [M].北京:科学出版社,2002.
[4]ALLEN J Bard,LARRY R Faulkner.Electrochemical methods-fundamentals and applications (second edition)[M].New York:John Wiley&Sons,Inc.,2010.
[5]金涛,何卫平,廖圣智,等.2024-T62铝合金涂层外场腐蚀环境下电化学性能研究 [J].装备环境工程,2016,33 (1):8-13; 28.
