准平行光干涉的滤波型多抖动相控方法研究

柴金华 陈飞

(陆军炮兵防空兵学院军用光电工程教研室,合肥 230031)

1 引 言

准平行光干涉是多个激光束之间的干涉,光束之间有一定夹角,但夹角很小,即光束与光束之间是准平行的,从而在远处仍然可以有较大重迭区域.准平行光干涉有很多应用,其需求是使干涉区域中干涉极强光斑始终作用于目标,而做到这一点的关键是要实时进行相位控制,这种相控方法可以借鉴光纤激光器的相干合成方法[1−6].

目前相干合成有多种方法,例如外差锁相法[7,8]、随机并行梯度下降算法[9−12],自参考自同步锁相法[13−15]以及多抖动法[16−21]等.外差法需要一束参考光,同时对光纤激光器准直阵列和光纤激光器探测器阵列排布要求比较高.而随机并行梯度下降算法不需要参考光束,只需要一个光电探测器,对光纤激光器准直器阵列排布要求不高.但是要执行梯度下降算法,对算法的执行效率和计算机的处理能力有较高的要求[10].

相比以上两种方法,多抖动法不需要参考光,只需要一个光电探测器,实验光路较为简单.设定多个频率的正弦信号加载在相位调制器,通过乘法器和积分器的相关检测方法实现相位差的识别与反馈信号的输出[16,17].考虑到抖动法不需要参考光的优势,本文提出一种滤波型多抖动相控方案.首先进行该方案的理论分析,并在此基础上阐明滤波型多抖动相控原理,然后进行数值分析与模拟实验,以说明滤波型多抖动相控方法的可行性.

2 准平行光干涉的滤波型多抖动相位控制方案

准平行光干涉的滤波型多抖动相位控制系统主要由激光器、分束器、相位调制器、单模光纤、光纤准直器、光电探测器、光电信号放大电路、相位差检测器以及信号发生器组成.

以二路准平行光干涉相位控制为例.如图1所示,激光器发出的激光经过分束器分为两束,两光束在光纤中传播,并受到相位调制器调制,每束光最后经光纤准直器准直,在远场目标区实现准平行光干涉,光电探测器测得远场某点干涉信号后,经光电信号放大电路再经相位差检测器得到相位控制信号V1和V2,并加载在相位调制器上调节光束相位,校正光束间的相位差.当光束间的相位差为0或者2π的整数倍时得到光强的极大值.信号发生器的作用是为相位调制器提供调制信号V0sinω1t和V0sinω2t.

图1 二路准平行光干涉相位控制示意图Fig.1.Schematic diagram of phase control of two beams of quasi parallel light interference.

图2 N路准平行光干涉相位控制示意图Fig.2.Schematic diagram of phase control of N beams of quasi parallel light interference.

同理,N路准平行光干涉相位控制方案如图2所示.

3 准平行光干涉的滤波型多抖动相位控制的理论依据

以二路准平行光干涉为例,在直角坐标系中,假设两束准平行光同时沿z轴传播,那么波前z=0处的干涉光强表达式为

其中I1和I2分别为两束光的光强;第三项为干涉项;其中k为波矢量大小;α1,β1为光束1与x轴、y轴的夹角;α2,β2为光束2与x轴、y轴的夹角;φ10,φ20分别为光束1和光束2的初相位.采用LiNbO3晶体相位调制器,那么,

V1和V2是直流控制电压,V0sinω1t和V0sinω2t分别是两光路上相位调制器的调制信号,l1和l2分别是两光路上的光纤长度,n是光纤的折射率,n0是LiNbO3晶体的折射率,r33为LiNbO3晶体的电光系数,d是LiNbO3晶体波导厚度,l为LiNbO3晶体波导长度.

为了简明起见,做如下定义.

光纤长度及光束夹角引起的相位延迟及相位差

控制电压引起的相位延迟及相位差

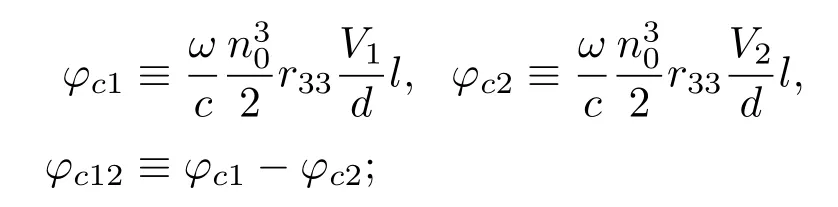
总的相位差

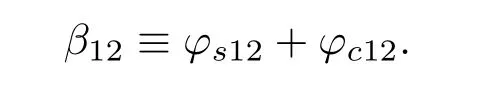
由此可得:

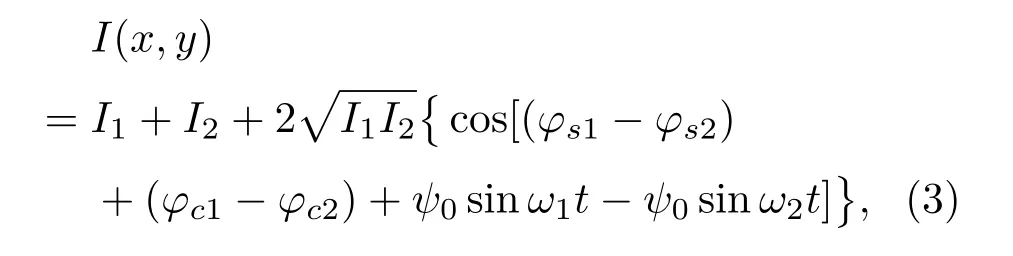
即

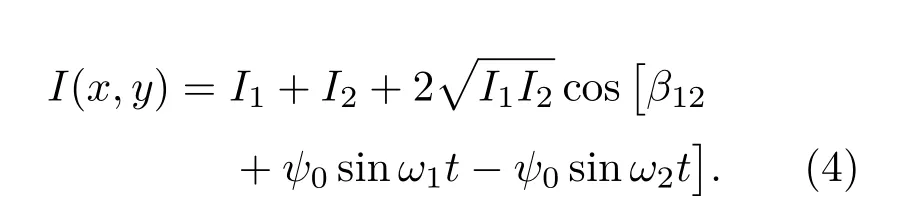
再将(4)式展开可得:

利用数学关系式

将(6)式代入(5)式,考虑到贝塞尔函数随着阶数的增大,当ψ0较小时,J值将趋于0,所以只考虑0,1,2阶项,得到光强公式:

根据贝塞尔函数的多项式展开式[22],当ψ0较小时忽略公式中ψ0的3次项以及3次以上的项,即忽略(7)式中J1J2项和J2J2项,可得二路准平行光干涉光强公式:

对于二路准平行光干涉光路,可以考虑一路有相位调制器,一路无相位调制器的简单情况,重复上述步骤得到:

在ψ0值很小的情况下,J0(ψ0)的值比J1(ψ0)和J2(ψ0)的值大得多,此时cosβ12包含项的值也要大于sinβ12包含项的值.要使光强尽可能大,就要使cosβ12尽量大,而sinβ12尽量小.光强取得极值的条件为β12为0或者2π的整数倍.

采用上述推导方法,同样得到三路准平行光干涉强度公式:

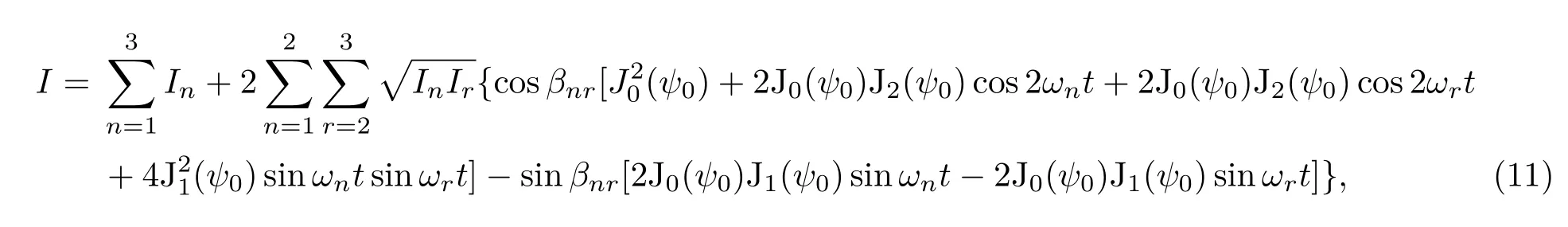
其中,β12是光束1和2之间的相位差,β13是光束1和3之间的相位差,β23是光束2和3之间的相位差.

同样得到四路准平行光干涉强度公式

同理得N路准平行光干涉的光强公式

其中,βnr是各光束之间的相位差,式中sinωntsinωrt也可用差频项cos(ωnt−ωrt)与和频项cos(ωnt+ωrt)来表示.

4 准平行光干涉的滤波型多抖动相位控制原理

以二路准平行光干涉为例.由(9)式可知,要想得到二路干涉相干光强的极大值,就要使得β12是0或者2π的整数倍,满足此条件时,光强信号中含有sinω1t项和sinω2t项的值应为0.因此只需检测光电信号中含有sinω1t项和sinω2t项的值是否为0,以此作为相位控制的依据.具体做法是:分别设置中心频率为f1和f2的带通滤波器,经过测幅电路得到直流电压信号,将直流电压信号放大加载至相位调制器进行相位的校正.

扩展到N路的情形,根据(13)式可知cosβnr后含的项当中含有调制频率的二倍频项以及和频项和差频项,为使信号处理方便,不能任意选取调制频率.为此,设定各路信号的调制频率为:f1,3f1,5f1···,(2N−1)f1.这样做的目的是使cosβnr后的频率项均为f1的偶数倍频项,而sinβnr后的项均为f1的奇数倍频项,便于滤波器进行信号的分离,实现相位差信号的提取.

相位差检测器是实现相位校正的关键器件,相位差检测器原理如图3所示.图中滤波器ω1,ω2,···,ωN用来识别sinω1t项,sinω2t项,···,sinωNt项的值是否为0,如果不为0,后续测幅电路1,测幅电路2,···,测幅电路N分别测出直流电压,经直流放大器放大,形成相位控制电压V1,V2,···,VN分别加载到各光路的相位调制器上.

图3 相位差检测器原理图Fig.3.Principle diagram of phase difference detector.

假定光电探测器的响应灵敏度为M,光电探测器的光敏面面积是S,那么输出的光电流可表示为

经过光电信号放大电路转换为电压信号,光电信号放大电路的增益为A,电流流经的电阻阻值为R,那么输出信号可以表示为

输出信号分别进入N路中心频率不同的带通滤波器,带通滤波器的增益是B,第1路到第N路的信号分别是:

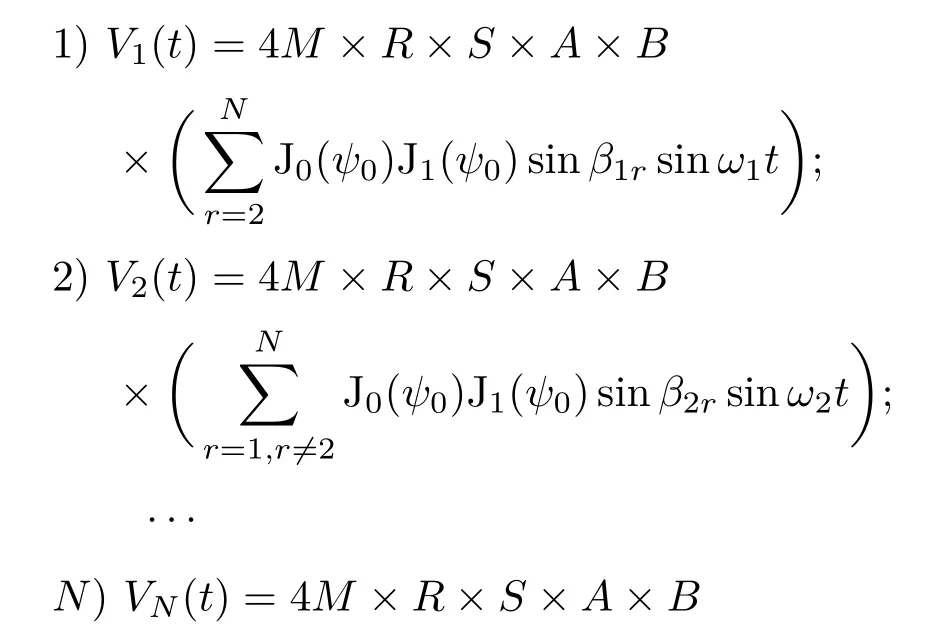
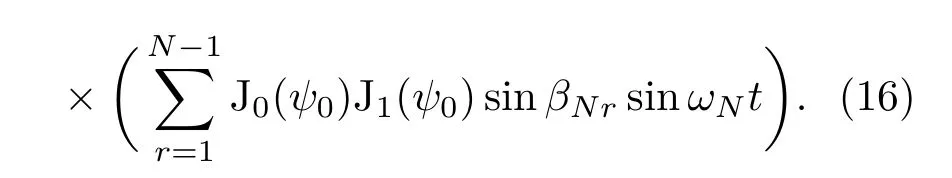
幅度测量电路对光电信号幅度进行测量,后经直流放大电路得到相位控制电压.采用单向正电压控制,假定直流放大电路的增益分别是F1,F2,···,FN,各路施加的相位控制电压可以表示为:

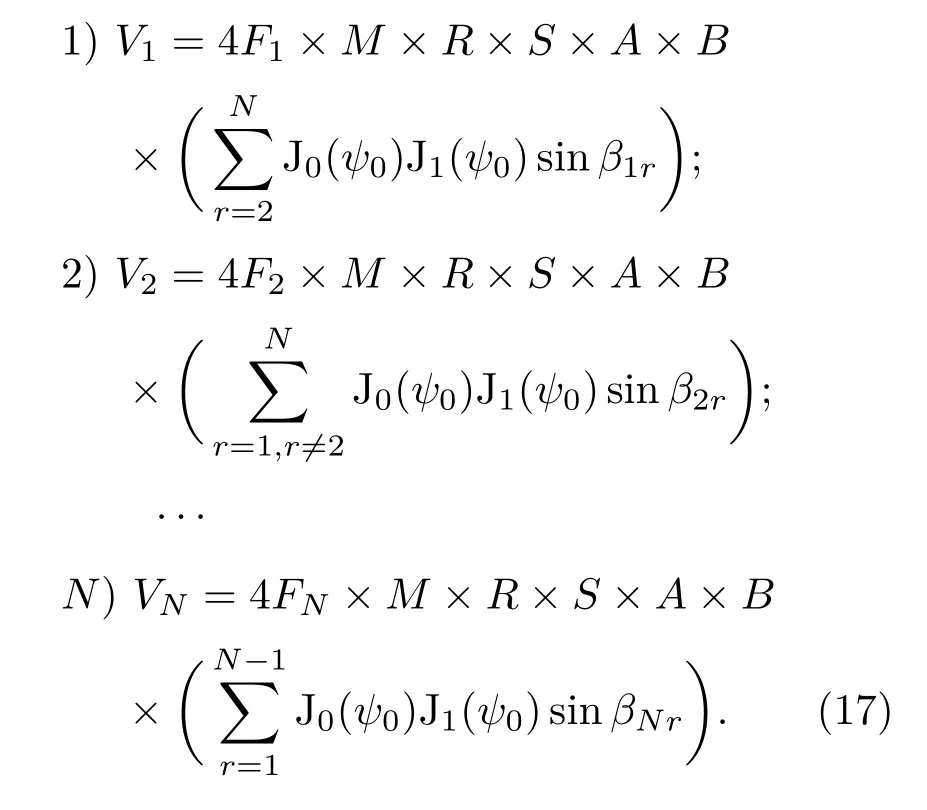
将各路的相位控制电压分别加载到各路的相位调制器上,使相位调制器调整光束的相位,最终实现各光束之间相位的校正.

5 滤波型多抖动相位控制的数值分析与模拟实验

5.1 数值分析

以(10)式为基础,对干涉光强分布进行数值分析.取调制正弦波信号幅度为0.3 V,频率为5 kHz,两光束相位差β12范围为0—2π,相位差取典型值时光强的数值曲线如图4所示,其中上方的曲线是干涉光强曲线,下方的曲线是经过滤波器之后的滤波曲线.

图4 光强随时间的变化 (a)β12=0;(b)β12= π/6;(c)β12= π/3;(d)β12= π/2;(e)β12=2π/3;(f)β12=5π/6;(g)β12= π;(h)β12=7π/6;(i)β12=4π/3;(j)β12=3π/2;(k)β12=5π/3;(l)β12=11π/6;(m)β12=2πFig.4.Curve of light intensity via time(a)β12=0;(b) β12= π/6;(c)β12= π/3;(d) β12= π/2;(e)β12=2π/3;(f)β12=5π/6;(g)β12= π;(h)β12=7π/6;(i)β12=4π/3;(j)β12=3π/2;(k)β12=5π/3;(l)β12=11π/6;(m)β12=2π.

图4(a)的情形,相位差β12=0,光强的最大值约为4,光强曲线幅度最小,由(10)式可知,此时光强表达式中只含有调制频率f1的2倍频项,即光强曲线的频率为10 kHz,滤波信号此时输出为0,滤波曲线与坐标横轴重合;相位差从0到π/2变化的过程中,如图4(b)—(d),光强表达式中调制频率的2倍频项不断减小,而调制频率项不断增大,光强曲线的波动增大,滤波信号的频率为5 kHz,滤波信号振幅不断增大,相位差等于π/2时,光强表达式中只含调制频率项,即光强曲线的频率为5 kHz,滤波信号幅度达到最大;相位差从π/2到π的变化过程如图4(d)—(g),与相位差从0到π/2变化的过程相反,相位差等于π时,光强值降至最低,此时光强变化的幅度也最小,光强曲线的频率也是10 kHz,滤波信号输出为0,滤波曲线同样与坐标横轴重合.同理,相位差从π到2π的变化过程与0—π的过程类似.

5.2 模拟实验

按照准平行光干涉的相控方案,当激光器参数确定,光纤光路确定,光纤准直器布局确定,亦即准平行光在空间的角度确定,目标区某点的光强完全取决于总相位差β12(以二路为例);而β12完全由反馈回路及相位调制器进行校正,最终实现光强最大.这样可以用模拟实验来模拟相位控制的过程,因而可以考虑将光纤准直器所发射的空间光束的相干用光纤耦合器中两束光相干来模拟,为此,采用光纤M-Z干涉型光路模拟远场某一点光强变化情况,光电信号变化即为干涉光强变化,由示波器记录变化波形.

实验装置如图5所示,主要有1550 nm窄线宽激光器、单模光纤、光纤耦合器、相位调制器、直流稳压电源、PIN型光电探测器,光电信号放大电路、UAF42带通滤波器模块、AD637有效值检测模块、OP07加法器模块、TLC2652直流电压放大电路模块,信号发生器以及示波器.

按照激光器、信号发生器、示波器、直流稳压电源的顺序依次打开电源.调制正弦波信号的幅度是0.3 V,频率是5 kHz.首先断开反馈控制回路,示波器记录波形,此时图5中1○端口输出的是相控前的滤波波形,2○端口输出的是相控前的干涉波形.随后在系统中接入AD637有效值检测模块以及TLC2652直流电压放大电路模块,反馈控制电压信号通过OP07加法器模块加载到相位调制器上,利用示波器记录波形,此时1○端口输出的是相控后的滤波波形,2○端口输出的是相控后的干涉波形.模拟实验的实物图如图6所示.

示波器记录相位控制前后典型情形下的波形如图7所示.图中,上方波形(CH1通道)为滤波波形,下方波形(CH2通道)为干涉波形.

利用电压表测量各情形的相位控制电压,得到相位控制电压数据如表1所列.

表1 不同情形的相位控制电压输出(V)Table 1.Output voltage of phase control in different cases(V).

从示波器上读取相控前后干涉波形的电压值的最大值,它反映了相控前后光强的最大值,数据如表2所列.

图5 滤波型多抖动相位控制的模拟实验框图Fig.5.Frame diagram of simulation experiment of fi lter type multi-dithering phase control.

图6 滤波型多抖动相位控制的模拟实验实物图Fig.6.Device diagram of simulation experiment of fi lter type multi-dithering phase control.

图7 实验中典型情形的波形图 (a)情形1;(b)情形2;(c)情形3;(d)情形4;(e)情形5Fig.7.Diagram of wave pattern for typical cases in the experiment:(a)Case one;(b)case two;(c)case three;(d)case four;(e)case fi ve.

表2 不同情形下相控前后光强最大值(以电压值表示)Table 2.Maximum of light intensity before and after phase control in different cases(represented by voltage value).

图7(a)相控前后的波形变化很小,干涉波形的最大值分别为720 mV和728 mV.728 mV是实验中获得的最大值,滤波波形幅度很小,主要来自电路噪声.对比图4(a)情形,图4(a)的中干涉波形的最大值为4,达到了整个数值分析的最大值,滤波波形的幅度为0.可见,图7(a)对应图4(a),即相位差为0的情形.此时实验测得的相位控制电压为0.03 V,相控作用可忽略.

图7(b)中相控前干涉波形的最大值为616 mV,滤波波形有一定幅度.对比图4(a)—(d)的波形变化,按照光强最大值的数值比例考虑,可知图7(b)相控前对应图4(a)—(d)之间的某情形,即相位差在0—π/2的某种情形.图7(b)相控后干涉波形的最大值为432 mV,滤波波形有一定幅度.对比图4(g)—(j)之间的波形变化,按照光强最大值的数值比例考虑,可知图7(b)相控后对应图4(g)—(j)之间的某情形,即相位差在π—3π/2的某种情形.实验测得的相位控制电压为3.15 V,通过相位控制,相位差向2π方向校正.

图7(c)相控前干涉波形的最大值为520 mV,相控前的滤波波形的幅度最大,频率为5 kHz.对比图4(d)的情形,图4(d)中干涉波形的最大值为2.5,滤波波形幅度最大,频率为5 kHz.可见,图7(c)相控前对应图4(d),即相位差为π/2的情形.实验测得的相位控制电压为4.45 V.图7(c)相控后的干涉波形的最大值为720 mV,接近于整个实验最大值的情形,采用的是正向电压控制,可见图7(c)相控后对应图4(m),即相位差为2π情形,而不是图4(a)相位差为0的情形.

图7(d)相控前后干涉波形的最大值分别为408 mV和592 mV,滤波波形有一定幅度.按照上述同样的思路分析可知,图7(d)相控前对应图4(d)—(g)之间的某情形,即对应于相位差在π/2和π之间的某个值,且更接近于π/2的某种情形. 图7(d)相控后对应图4(g)—(m),即3π/2和2π之间的某个值.实验测得的相位控制电压为3.07 V,通过相位控制,相位差向接近于2π方向校正.

图7(e)相控前后的波形变化也很小,干涉波形的最大值分别是280 mV和304 mV.280 mV是实验中获得的最小值,滤波波形的幅度也很小,主要来自电路噪声.对比图4(g)的情形,图4(g)中干涉波形的值接近于0,达到了整个数值分析的最小值,滤波波形幅度为0.可见,图7(e)对应图4(g),即相位差为π的情形.此时实验测得的相位控制电压为0.04 V,相控作用很小.

综合所述可知,相位差在0—π/2,π/2,π/2—π所代表的各种情形,均有相位控制电压的输出,并且校正相位差,使相位差向2π方向校正.

需要说明的是相位差为0时,产生很小的相位控制电压,使得相位差在0附近;而相位差为π时,也产生很小的相位控制电压,但相位校正的过程不断进行,使得相位差向2π方向校正.

实验中相位变化主要源于单模光纤的双折射,导致波形的周期性变化.由于波形变化是缓慢的,能够反映出相控前后波形的明显变化.

5.3 相位控制的性能分析

首先对相位控制实验的控制带宽进行分析.控制带宽反映了系统的响应速度,控制带宽越大,系统的响应速度就越快[23].实验的控制带宽主要与相位控制器件的响应速度有关,包括:

1)光电探测器的响应时间为t1;

2)光电信号放大电路的响应时间为t2;

3)带通滤波器电路的响应时间为t3;

4)幅度检测电路的响应时间为t4;

5)直流电压放大电路的响应时间为t5;

6)相位控制信号加载到相位调制器的传输时间为t6.

假设一次相位控制的时间为T,那么时间T可以表示为

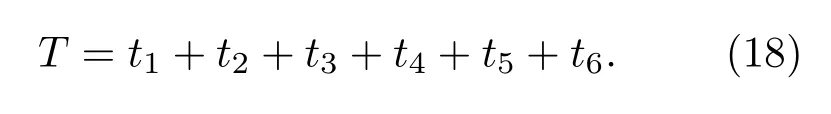
光电探测器的响应时间为纳秒量级时,t1可以忽略;实验中所用光电信号放大电路的主控芯片OP37的带宽增益积为63 MHz(即信号放大倍数与带宽的乘积),电路放大倍数为10倍,那么此时带宽为6.3 MHz,远高于调制频率,因而t2可以忽略;AD637有效值测量电路在小幅度情况下的带宽在1 MHz以上,远高于调制频率,因而t4可以忽略;TLC2652带宽增益积为1.9 MHz,放大倍数为100倍,那么带宽为190 kHz,因而响应时间为5.3µs;调制信号和相位控制信号加载到相位调制器的传输时间t6忽略不计.所以,实际的相位控制时间主要考虑滤波电路响应时间t3和直流电压放大电路的响应时间t5,带通滤波器的中心频率为5 kHz,带宽为2.5 kHz,响应时间为0.4 ms,此时电路的响应总时间近似为T1,则T1=t3+t5,因而实验的控制带宽可以表示为

当采用带宽更宽、性能更加优良的带通滤波器后,实验的控制带宽还能进一步提高.

实验中测得的相位控制信号输出电压范围是0.03—4.45 V,根据(17)式,相位控制电压的大小与滤波信号的幅度成正比,相位差为π/2时产生的相位控制电压最大,要使相控后相位差达到2π,那么此时相位控制所要达到的量应为3π/2,实验所用相位调制器的半波电压约为3.1 V,对应的相位控制电压理论值应为4.65 V,实验中测得最大输出电压为4.45 V,实测的最大控制电压与理论值接近.

6 结 论

提出了一种准平行光干涉的滤波型多抖动相控方案,给出了滤波型多抖动相控理论分析,并进行了数值分析和模拟实验研究,分析了相控前后干涉波形的变化,说明了相控方法的有效性.

滤波型多抖动法与经典的多抖动法都是利用调制频率来识别相位差,所不同的是滤波型多抖动法是通过滤波来识别相位差,通过测幅电路实现反馈电压输出.而经典的多抖动法是通过乘法和积分电路实现相位差的识别与反馈电压输出[16,17,19].因为乘法器要求参考信号的幅度很小,因此造成了参考信号的取值范围很小.同时还要考虑积分时间与调制周期的关系,通常要求积分时间是调制周期的10倍以上,降低了系统的控制带宽[17],而滤波型多抖动法的反馈回路不需要参考信号.另外,处理多路信号时,滤波型多抖动法采用信号并行处理的方法,各路之间的信号不影响,因而随着光束数目的增多对于控制带宽无明显影响.而经典的多抖动法随着光束数目的增多,容易造成光束间相位变化混乱,控制算法的复杂度提高,导致处理速度变慢,从而降低了系统的控制带宽[19].

模拟实验得到的滤波型多抖动法的控制带宽约为2.5 kHz,采用并行处理的方法,光束数目增多时不会降低控制带宽,相位控制信号的输出范围是0.03—4.45 V.以上表明,该方法也是一种可用的相控方法.

滤波型多抖动相控方法,用滤波器来识别各频率对应项的值是否为0,此时相位差为2π的整数倍,通过反馈控制使得两束光的相位锁定到同相.在实际应用中,也有可能需要将相位锁定在任意相位,此时通过滤波器的各频率对应项的值不再是零值,将此非零值作为参考值,偏离此参考值则反馈相位调制器,同样可以将相位锁定在任意相位上.

在实验中,用光纤M-Z干涉的光强模拟准平行光空间干涉的某一空间点的光强,这主要是考虑到M-Z干涉容易实现,且不影响相位控制反馈回路的研究.如果要分析准平行光干涉在相控情况下光强的空间分布,则需要采用光纤准直器构成准平行光的空间干涉,对该问题将做进一步研究.另外,以二束光实验来证实相控反馈的可行,以此相控回路为基本单元将为三束光以及三束以上的多光束实验研究奠定基础.

[1]Liu Z J,Hou J,Xu X J,Feng Y,Zhou P,Ma Y X,Wang X L,Lei B,Cao J Q 2009Chin.J.Lasers36 2773(in Chinese)[刘泽金,侯静,许晓军,冯莹,周朴,马阎星,王小林,雷兵,曹涧秋2009中国激光36 2773]

[2]Wang X L,Zhou P,Xu X J,Liu Z J,Chen Z L,Ma Y X,Ma H T,Li X,Zhao Y J 2009Laser&Optoelectronics Progress05 13(in Chinese)[王小林,周朴,许晓军,刘泽金,陈子伦,马阎星,马浩统,李霄,赵伊君 2009激光与光电子学进展05 13]

[3]Goodno G D,Komine H,McNaught S J,Weiss S B,Remond S,Long W 2006Opt.Lett.31 1247

[4]Fan T Y 2005IEEE J.Sel.Top.Quantum.Electron.11 567

[5]Underwood K J,Jones A M,Gopinath 2015Appl.Opt.54 5624

[6]Uberna R,Bratcher A,Tiemann B 2010Appl.Opt.47 6762

[7]Wang D T,Zhou W J,Wen W F,Peng Q X,Li Z R,Hu W H,Li Z J 2013High Power Laser Part.Beams25 1125(in Chinese)[王德田,周维军,温伟峰,彭其先,李泽仁,胡文华,李忠建2013强激光与粒子束25 1125]

[8]Xiao R,Hou J,Jiang Z F 2006Acta Phys.Sin.55 184(in Chinese)[肖瑞,侯静,姜宗福 2006物理学报55 184]

[9]Zhou P,Ma Y X,Wang X L,Ma H T,Xu X J,Liu Z J 2009Chin.J.Lasers36 2972(in Chinese)[周朴, 马阎星,王小林,马浩统,许晓军,刘泽金 2009中国激光 36 2972]

[10]Huang Z M,Tang X,Liu C L,Li J F,Zhang D Y,Wang X J,Han M 2015Chin.J.Lasers42 41(in Chinese)[黄智蒙,唐选,刘仓理,李剑锋,张大勇,王小军,韩梅2015中国激光42 41]

[11]Zheng Y,Shen F 2010Chin.J.Lasers37 631(in Chinese)[郑轶,沈锋2010中国激光37 631]

[12]Mourou G,Brocklesby B,Tajima T,Limpert J 2013Nature Photon.07 258

[13]Shay T M,Benham V,Baker J T 2006Opt.Express25 12022

[14]Shay T M,Benham V,Baker J T 2007IEEE J.Sel.Top.Quantum.Electron.13 480

[15]Vorontsov M A,Weyrauch T,Beresnev L A,Liu L 2009IEEE.J.Sel.Top.Quantum.Electron.15 269

[16]Ma Y X,Wang X L,Zhou P,Ma H T,Zhao H C,Xu X J,Si L,Liu Z J,Zhao Y J 2010High Power Laser Part.Beams22 2803(in Chinese)[马阎星,王小林,周朴,马浩统,赵海川,许晓军,司磊,刘泽金,赵伊君 2010强激光与粒子束22 2803]

[17]Ma Y X,Si L,Dong X L,Zhou P,Xu X J 2012Chin.J.Lasers39 0031(in Chinese)[马阎星,司磊,董小林,周朴,许晓军2012中国激光39 0031]

[18]Shay T M,Benham V 2004Proc.SPIE5550 313

[19]Ma Y X 2012Ph.D.Dissertation(Changsha:National University of Defence Technology)(in Chinese)[马阎星2012博士学位论文(长沙:国防科技大学)]

[20]Lin L,Loizos D N,Vorontsov M A,Cauwenberghs G 2007SPIE6708

[21]Jolivet V,Bourdon P,Bennal B,Lombard L,Goular D 2009IEEE.J.Sel.Top.Quantum.Electron.15 257

[22]Liang K M 2006Methods of Mathematical Physics(Beijing:Higher Education Press)p247(in Chinese)[梁昆淼2006数学物理方法(北京:高等教育出版社)第247页]

[23]Wen W F,Wang D T,Zhou W J,Peng Q X 2014J.Detect.Control36 11(in Chinese)[温伟峰,王德田,周维军,彭其先2014探测与控制学报36 11]