一种对流传质传热模拟方法：考虑土豆片中三种不同流体速度

王小勇++刘显茜

摘要：许多文献报道了土豆片干燥模拟方法。然而，其并没有清晰解释传热传质耦合机理。本文建立一个模型来描述土豆片中的温度演化和水分迁移。创新点是考虑到土豆片中存在三种不同流体速度以及认为材料物理变量之间相互影响。模拟证明计算结果与文献实验具有良好的拟合度。同时研究了不同的风温，风速以及空气相对湿度对干燥的影响。

Abstract： Many simulation methods of drying potato slices were reported. However， this did not explain the coupled mechanism of heat and mass transfer clearly. A model is built to describe the temperature evolution and moisture immigrates of potato slices. The innovation point is considering that the coefficients will alter over other physical variables and the existence of three different fluid velocity in the porous medium. Then， a good fitting between literature experiment and calculation result can be observed. And， the effects of parameters such as temperature， air velocity and air relative humidity towards drying rate are researched.

关键词： 耦合机制；流体速度；物理变量

Key words： coupled mechanism；fluid velocity；physics variables

中图分类号：TK124 文献标识码：A 文章编号：1006-4311（2018）08-0176-05

0 引言

食品干燥是一个重要的工业生产部门。深入地了解其干燥过程当中的热量和质量迁移对产品品质的提升和生产节能是至关重要的。然而，在多孔介质（生物材料都可以看成是多孔材料）传热传质是复杂的。其复杂性基于以下两个因素：干燥过程中占主导地位的传输机制的变化以及因水分蒸发等因素导致的多孔介质物理参数的显著变化[1]。

Sander等人[2]，Nasrallah等人[3]，以及Sun等人[4]进行了广泛的多孔介质数值传热传质研究。Wang和Brenman[5]提出了一个以土豆为材料来计算其传热传质的数学模型，但他们忽略了干燥过程中水蒸气压力梯度的作用。Win-Jin Chang和Cheng-I[6]首先使用拉普拉斯变换处理耦合的传质传热偏微分方程，但是材料的物理参数和内部压力被认为是常数。Chandramohan[7]和Ahmet等人[8]提出计算公式中缺少对流项，导致计算精度不足。

此外，物理参数的使用也会影响计算结果的可信度和精度。Jaruk和John[9]预测了在对流热风干燥条件下土豆和胡萝卜中水分含量，但其使用的是实验中测量的有效水分扩散系数。Hussain和Dincer[10]提出了一个二维湿圆柱体传热传湿分析，其水分扩散系数由阿仑尼乌斯方程计算的，只与温度相关。针对芒果的对流干燥过程，Barati和Esfahani[11]给出了一种新的解法，但其假设芒果的物理参数是恒定不变的。

本文的目的是在土豆切片干燥过程中考虑不同驱动力和多变参数来解决其的传热传质耦合计算问题。此外，收缩效应不可忽略，考虑采用有效蒸发率法。因此，本文将在第二部分中定义控制方程和介质性质，并对第三部分中进行计算结果进行分析。

1 物理模型和数学理论

1.1 物理模型

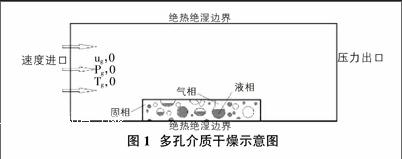
本文的物理模型基于多孔介質理论。图1表示了多孔介质干燥示意图。从图中可以看出，多孔介质分为三个部分：固相（干基），液相以及气相（含湿空气）。因此，多孔介质的一些物理参数需要定义。

1.2 参数

孔隙度：孔隙度？准是指多孔介质中非固相所占有的体积V？准与整个介质的总体体积V之比，其被定义为：

水饱和度：水饱和度Sl是孔隙中液相水占有的体积Vl与孔隙总体体积V？准之比，可表示为：

有效系数：有效密度由多孔介质中的固相密度ρeff，液体水密度ρl和湿空气密度ρma组成。基于体积平均法，其可计算为：

其中，湿空气密度ρma可计算为：

公式（4）中，Pma，P0分别是湿空气气压，管内初始气压。Ml， Ma分别是液态水与干燥空气的摩尔质量。Xv，Xa分别是湿空气中水蒸气与干燥空气的摩尔分数，两者数学关系和计算如下：Xa+Xv=1（5）

Tma为多孔介质中湿空气温度，R为摩尔气体常数。cv表示材料内的水蒸气浓度。

同理，按照体积平均理论，有效比热容和有效传热系数可分别定义成：

其中，Cp，s，Cp，l分别为多孔介质中的固相和液相比热容。ks，kl分别为多孔介质中的固相和液相的传热系数。Cp，ma，kma分别为多孔介质内的有效比热容和有效传热系数，其可分别定义为：

Mma为湿空气的摩尔质量，其由分数加权计算为：

Cp，v，Cp，a分别为水蒸气和干空气比热容。kv，ka分别为水蒸气和干空气传热系数。θaa，θav，θvv，θva为湿空气传热系数参数因子，定义为：

1.3 数学理论

本文基于一些基本假设。

①多孔介质中的各相分布是均匀的。

②所有相（固相、液相和气相）是连续体。

1.3.1 质量传递

①管内空气传递。

使用N-S方程和连续性方程，管内空气传递方程为：

上述方程中，对于初始的速度值ug，0和压力值Pg，0均是定值。？籽g的变化取决于管道内的相对湿度的变化。

②多孔介质内湿空气传递。

考虑到湿空气在多孔介质内的流动，使用Wooding方程：

其中，湿空气质量源在多孔介质与水活度aw相关，其由以下公式计算[12]

同时，湿空气粘度系数？浊ma由以下公式计算

其中？着p是无液相孔隙内的湿空气体积占比，可计算为：

此外，收缩效应不可忽略，考虑采用有效蒸发率，Keff。

③多孔介质内液态水传递。

介多孔质内液态水传递遵循以下方程：

应用达西定律同时忽略介质内的毛细现象，ul为液相速度，可计算为：

④多孔介质内水蒸气传递。

多孔介质内水蒸气传递遵循以下方程：

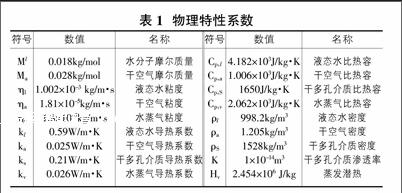
所有的物理特性系数在表1中列出。

2 结果和讨论

2.1 实验验证

计算和实验结果显示在下面。图2和图3是比较了气流速度为2.5m/s，空气温度为50℃，空气相对湿度为10%的计算结果与实验结果[14]。MR为干基含水率。

从图2和图3中均可以看出，计算结果和实验结果拟合地非常好。拟合系数分别达到0.998，0.997，0.994，0.999。

2.2 计算结果分析

对比图2和图3会发现两者在相同的尺寸的条件下其达到绝干的时间会有所差别。原因在与对干燥材料的处理的不同。经过水处理的土豆由于水的浸润作用而使其失去了活性，也就是说其组织细胞内的结合水溢出，加快了其水分的迁移速率，才会出现上述情况。

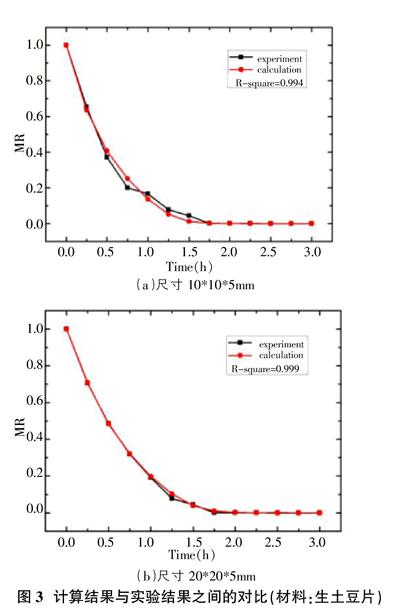
图4和图5分别展示了不同时间点时在长度和厚度方向上的干基含水率分布和温度分布。其数据分别取自于多孔介质的长度和厚度方向的中心线。

从图4（a）可以看出，其干基含水率-长度曲线类似于抛物线，出现了多孔介质中间干基含水率高两边干基含水率低的现象。其原因是因为多孔介质的两边的温度上升的快而中间温度上升的慢，导致其中间的干基含水率相对两边高，这可以从图5（a）中得到证实。

从图4（b）可以看出在厚度方向上的干基含水随着厚度增大而减少，那是因为热量传导至多孔介质的内部而使水分蒸发需要一定的时间，介质的内部有一个升温过程，其可由图5（b）得到证实。

2.3 参数的影响

图6，图7和图8展示了在不同的空气参数的影响下的干基含水率-时间曲线图。从图6可以看出，随着风温的增大，达到绝干的时间越短，那是因为温度的上升加快了水分子的热运动。图7也出现了与图6类似的现象，即随着风速上升多孔介质达到绝干的时间相应的下降。

但图8却出现了与图6和图7不同的变化趋势。即随着空气相对湿度上升多孔介质达到絕干的时间没有太大的变化。出现这种现象的原因极有可能是材料内部与空气的水蒸气压力差对干燥的影响程度很小。而且由此可以合理的推论，倘若加大干燥空气的相对湿度，当其大于介质内部的相对湿度时，可能会出现多孔介质达不到绝干的情况。

同时对比图6，图7和图8会发现风温相对于风速和空气相对湿度对多孔介质达到绝干的时间的影响更为明显。即温度梯度相比于水蒸气压力梯度对介质的传热传质更为明显。

3 结论

本文在考虑介质中三种不同流体的流动的基础上研究了土豆片干燥过程。发现理论模拟结果与文献实验结果拟合的很好，证实了模型的有效性。计算结果表明了多孔介质中间和两边的温度以及干基水分含量存在的负相关关系。同时风温，风速，空气相对湿度对介质达到绝干时间的影响的模拟说明了温度相对于风速和空气相对湿度对介质传热传质的影响程度要大的多。

参考文献：

[1]AK Datta （2007）， Porous media approaches to studying simultaneous heat and mass transfer in food processes. Ⅱ： Property data and representative results. Journal of Food Engineering 80（1）： 96-110.

[2]A Sander， D Skansi， N Bolf （2003）， Heat and mass transfer models in convection drying of clay slabs. Ceramics International 29（6）：641-653.

[3]SB Nasrallah， P Perre （1988）， Detailed study of a model of heat and mass transfer during convective drying of porous media. International Journal of Heat & Mass Transfer31（5）：957-967.

[4]LM Sun， NB Amar， F Meunier （1995）， Numerical study on coupled heat and mass transfers in an absorber with external fluid heating. Heat Recovery Systems and Chp 15（1）： 19-29.

[5]N Wang， JG Brennan （1995）， A mathematical model of simultaneous heat and moisture transfer during drying of potato 24（1）： 47-60.

[6]WJ Chang， CI Weng （2000）， An analytical solution to coupled heat and moisture diffusion transfer in porous materials. International Journal of Heat and Mass Transfer 43（19）：3621-3632.

[7]VP Chandramohan （2016）， Experimental analysis and simultaneous heat and moisture transfer with coupled CFD model for convective drying of moist object. International Journal for Computational Methods in Engineering Science and Mechanics 17： 59-71.

[8]K Ahmet， A Orhan， D Ibrahim （2008）， Experimental and numerical investigation of heat and mass transfer during drying of Hayward kiwi fruits. Journal of Food Engineering 88（3）：323-330.

[9]J Srikiatden， JS Roberts （2008）， Predicting moisture profiles in potato and carrot during convective hot air drying using isothermally measured effective diffusivity. Journal of Food Engineering 84（4）： 516-525.

[10]MM Hussain， I Dincer （2003）， Two-dimensional heat and moisture transfer analysis of a cylindrical moist object subjected to drying： A finite-difference approach. International Journal of Heat and Mass Transfer 46（21）： 4033-4039.

[11]E Barati， JA Esfahani （2011）， A new solution approach for simultaneous heat and mass transfer during convective drying of mango. Journal of Food Engineering 102（4）：302-309.

[12]C Ratti， GH Crapiste， E Rotstein （2008）， A new water sorption equilibrium expression for solid foods based on thermodynamic considerations. Journal of Food Science 54（3）： 738-742.

[13]L Hassini， S Azzouz， R Peczalski， A Belghith （2007）， Estimation of potato moisture diffusivity from convective drying kinetics with correction for shrinkage. Journal of Food Engineering 79（1）： 47-56.

[14]AS Olawale， SO Omole （2012）， Thin layer drying model for sweet potato in tray dryer. Agric Eng Int： CIGR Journal 14（2）： 131-137.