基于城市道路拥堵的物流配送车辆停车收费定价研究

肖建华,陈 萍,刘秉镰

(1.南开大学 现代物流研究中心，天津 300071；2.南开大学 商学院,天津 300071；3.南开大学 中国特色社会主义经济建设协同创新中心，天津 300071)

一、引 言

城市交通路网是社会经济发展的载体，也是城市高效稳定发展的重要保障。随着城镇居民生活需求多样化、现代信息技术革新与市场商业体系发展、网络购物接受度的加强，城市配送日间需求大幅增长，城市道路拥堵现象、停车难等问题也日益凸显。据测算，2015年我国城市物流车辆年产量在220万辆到250万辆，预计到2020年将达到260万辆到290万辆。*数据来源：http://m.chyxx.com/view/424529.html。此外，据《中国城市配送市场发展蓝皮书2016》统计，中国城配货车已达1300万辆，数量为出租车的5倍，正逐渐成为城市交通拥堵的重要原因。Chow等(2010)、You等(2016)的研究也表明，随着城市配送需求的持续增长以及配送车辆运输效率低下，配送车辆加剧了城市的拥堵状况，并带来了安全性和空气质量等诸多新问题[1-2]。Jaller等(2013)在对纽约市货运需求的研究中，指出忽略城市货运车辆的停车政策是市中心道路经常陷入巨大交通拥堵的主要原因之一[3]。因此，如何优化城市配送车辆的日间出行时间，科学地缓解城市道路拥堵及城市停车难等问题具有重要的理论研究意义和现实价值。

停车收费政策作为一项缓解交通拥堵的高效措施，能够利用市场价格杠杆，合理调控车辆分流，优化交通需求结构，已在国外得到了较好应用和有效验证[4-6]。但总的说来，目前国内外学者都针对私家车实施停车收费政策来调控出行成本和引导居民出行方式决策，从而改善城市道路拥堵、停车难等问题。例如，Kepaptsoglou等(2010)通过为各类用户提供停车激励或抑制措施，提出了一个新方法来获得停车设施最佳定价方案，并利用遗传算法确定停车设施最优定价参数[7]；Feng等(2008)考虑交通管制、停车位供求关系和停车行为三类收费目的，建立了三种不同的路边停车费计算模型，并利用遗传算法优化该模型[8]；王健等(2013)以社会效益最大化为目标，建立了基于可变泊位容量的路内停车定价模型，并运用拉格朗日算法和平均值算法进行求解，验证了模型的可靠性[9]。与传统的城市停车收费政策相比，城市配送车辆由于具有交通方式较为单一等特性，通过收费调控其城市配送交通方式的手段将显得无能为力。

基于此，本文拟利用城市配送车辆时间的可微调性等特征，首次将时变停车收费措施引入到城市物流配送车辆的问题中，并以日间车辆平均拥堵程度最低和配送车辆停车缺口最小为目标，构建了基于城市道路拥堵的物流配送车辆停车收费定价双层规划模型。在下层车流分布模型中，本文创新性地将车辆不同时间的车流分布等价转化为经典的不同虚拟道路的空间车流分布模型。针对模型的NP难特性，本文提出了一种基于嵌入F-W迭代法的遗传算法求解该模型。最后，论文通过算例验证了模型及算法的有效性。

二、停车收费定价模型构建

(一) 问题描述

本文研究的问题可以描述为：假设某商业中心设有若干停车位供城市配送车辆停车使用，但由于其配送车辆的配送时间多集中于早、晚等高峰时段，配送时间与私家车的出行时间多有重叠，常造成商业中心的驶入道路交通拥堵及配送车辆的停车难等问题。与私家车的刚性出行需求不同，城市配送车辆的配送时间多具有一定的可微调性，本文拟提出对日间配送车辆实行分时段停车收费措施，以期缓解高峰时段的城市道路拥堵问题及配送停车难问题。本文假设收费政策不影响私家车的出行时间，也不会改变配送车辆的配送需求，且配送车辆能在一个时段内完成其配送任务。

(二) 符号说明

T：日间时段的集合；

qr：无停车收费时，r时段日间配送车辆到达量；

nt：有停车收费时，t时段日间配送车辆到达量；

wt：t时段出发的行驶时间，∀t∈T；

c：配送车辆的单位时间成本；

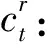
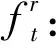
ut：t时段配送车辆停车位缺口量；

bt：t时段在道路上的私家车数量；

C：道路最大通行能力；

q：配送车辆停车位数量；

st：车辆到达时段与客户要求时段偏移所带来的惩罚成本；

pmin：停车收费最低指导价；

pmax：停车收费最高指导价；

k1：道路拥堵影响社会效益损失的重要度系数；

k2：停车位缺口影响社会效益损失的重要度系数，且k1+k2=1；

t0：道路不拥堵时的车辆行驶时间；

α,β：交通流量模型中流量-时间转换系数；

pt：t时段停车收费价格，∀t∈T；

(三) 模型构建

双层规划模型能较好地刻画各利益主体间的关系，在车辆收费问题中已经得到广泛的运用[10-11]，本文将采用双层规划模型来表征该问题，其上层模型表示城市停车收费管理部门的决策行为，决策变量是各时段的配送车辆停车收费价格；下层模型表示配送车辆针对给出的停车收费价格做出相应的最优决策，即配送企业以广义成本最小为目标选择配送服务到达时段。

(1)上层模型

(1)

s.t.

0≤nt+bt≤C,∀t∈T

(2)

pmin≤pt≤pmax,∀t∈T

(3)

其中，上层目标函数式(1)表示最小社会效益损失，包括拥堵路段的日间平均拥堵程度和配送车辆日间停车位数量缺口两部分；式(2)表示各时段道路上的车辆数量约束；式(3)表示各时段停车收费的价格约束。

(2)下层模型

根据随机用户均衡分配理论[12]，对由上层模型给出的停车收费方案，下层模型中有唯一平衡的配送车辆出行方案与之对应。下层模型为配送车辆选择到达时段模型，其目标函数为配送车辆出行广义配送成本最小。

(4)

s.t.

(5)

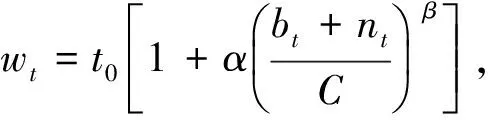
(6)

(7)

(8)

(9)

其中，下层目标函数式(4)表示最小化配送车辆出行的广义阻抗成本；式(5)表示配送车辆选择某时段的广义成本，该成本取决于三方面因素：出发时段的行驶时间成本、到达时段与客户要求时段偏移所带来的客户惩罚成本以及到达时段的停车收费价格；式(6)为时间交通流量关系模型；式(7)～(9)表示配送车辆到达数量平衡约束。

三、模型求解算法

双层规划模型的求解分为两个部分：一是利用随机用户均衡理论求解下层模型中的车流分布；二是求解上层模型中各时段停车收费价格pt。

(一) 求解车流分布

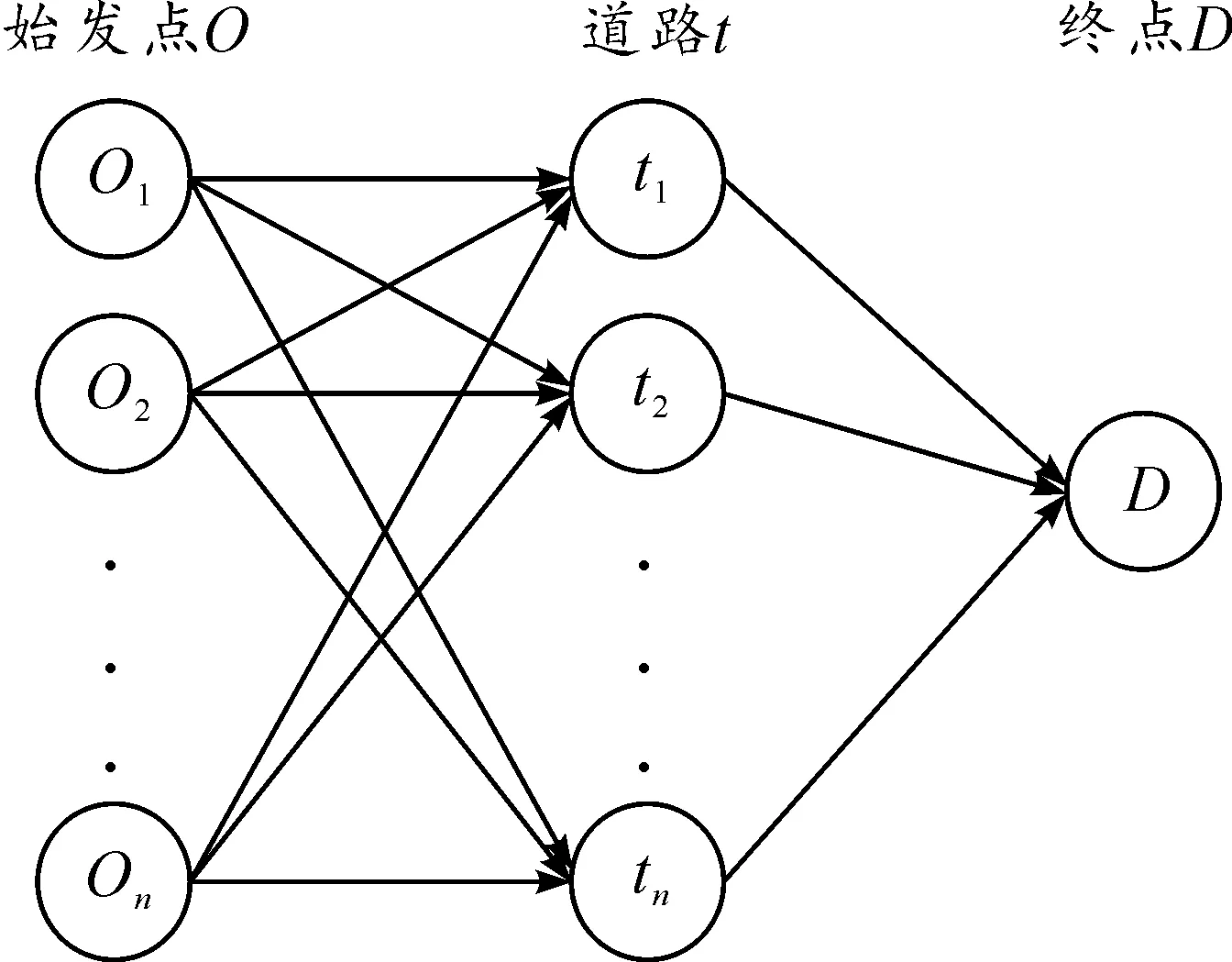
图1 配送车辆出行网络示意图

由于本文假定配送车辆能在同一时段内完成配送任务并离开，所以模型中各时段配送车辆分布问题可以等价转化为多个起始点O和单个终点D的流量分配问题，如图1所示。本文将客户要求的最佳出行时段转化为出始点O1,O2,…,On；将配送车辆实际出发时段转化为不同的路径选择t1,t2,…,tn；D代表最终到达的客户目的地。

F-W迭代法，也被称之为Frank-wolf算法，是一种利用线性规划思想设置最优步长重复迭代找寻最优解的算法。该算法具有操作简单、功能强大等特点，已广泛应用到求解各类交通流量模型[13-14]。根据F-W算法，本文规划模型中下层模型算法步骤如下：

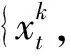
(二) 求解各时段停车收费价格

上层模型属于典型的NP-hard问题，国内外学者多用启发式算法对其求解。遗传算法作为经典的启发式算法，由于具有结构简单、功能强大等特点，广泛地应用于求解各类优化问题及停车收费定价等问题[7-8,15-16]，普遍取得较好效果。因此，本文也将利用基于嵌入F-W迭代法的遗传算法来求解城市配送车辆停车收费定价模型，其算法步骤如下：

步骤1：产生初始种群，对每条染色体运用F-W迭代法求解配送车辆车流分布，计算日间车辆通行时间，得到当前最优停车收费价格X及最优通行时间f(X)；更新当前最优解X*和最优值f(X*)，令X*←X,f(X*)←f(X)；

步骤2：使用轮盘赌方式，产生与初始种群数目相同的新种群；

步骤3：对新种群执行交叉和变异操作；

步骤4：对交叉变异后的新种群中每一条染色体运用F-W迭代法求解，得到当代最优解X和最优值f(X)。若f(X*)>f(X)，更新当前模型的最优解X*和最优值f(X*)，即令X*←X,f(X*)←f(X)；反之，则模型最优解X*和最优值f(X*)不变；

步骤5：重复步骤2～4至最大迭代次数；

步骤6：输出模型的最优解X*和最优值f(X*)。

四、算例分析：大型城市中心商业区域配送车辆调控分析

(一) 算例描述

表1 路网中12个时段私家车辆数及初始配送车辆数 (单位：辆)

资料来源：根据《中国城市配送市场发展蓝皮书2016》的配送车辆比例数据，由作者整理编制。

某城市核心区的配送需求由城市配送车辆完成，配送方根据客户需求时间范围，结合自身广义配送成本决定自身最优配送时间。日间配送时间分为早8点至晚8点共12个时段，各时段私家车辆数及日间配送车辆数如表1所示。

城市中由于路网承载力和车位有限，路网最佳通行车辆数为6500辆/小时，最大承载车辆数为9500辆，配送车辆的车位最大容纳能力为1350辆。假定配送车辆均为小型货车，每个时段中配送车辆完成运输及卸货作业，且所有配送车辆均可在原选定的配送时段前后移动两个时段，按时间先后顺序产生的相应客户满意度惩罚成本分别为30元、15元、20元和40元。

(二) 时变停车收费对车辆分流的影响

为研究时变停车收费措施对配送车辆分流的影响，本文利用基于嵌入F-W迭代法的遗传算法对算例进行求解。参考遗传算法经典文献对算法参数的指导取值范围及实验试算，本文算法的相关参数分别取值为种群规模为50，最大迭代次数为100，交叉率为0.5和变异率为0.2。此外，模型中其他相关参数为：c=70，pmin=5，pmax=30，α=0.15，β=4，t0=0.1，k1=0.34，k2=0.66。

利用改进的遗传算法，独立运行50次，得到各时段停车费用pt最优结果为5.0元、7.8元、12.1元、26.1元、29.0元、13.8元、16.7元、10.5元、24.3元、24.0元、5.3元和11.0元。停车收费前后各时段车辆总流量和配送车辆流量对比分别如图2和图3所示。

图2 停车收费前后各时段车辆总流量对比示意图

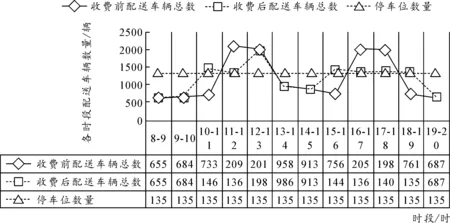
图3 停车收费前后配送车辆流量对比示意图

从图2和图3可以看出，在引入时变停车收费策略前，私家车辆和配送车辆集中在中午11:00-13:00和下午16:00-18:00，远远超过了停车位的最大容量，道路拥堵和停车困难显著。实施停车收费后，因为高峰时段设置的停车费用较高，部分配送车辆出现明显分流。调控结果显示，通过价格机制可以令配送车辆自主分流，有效缓解了高峰时段城市拥堵现象及城市道路停车难问题，也极大提高了低峰时期的路网使用效率。

(三) 重度拥堵路况下的时变停车收费策略优化

拥堵路况一般分为时段拥堵和重度拥堵两类，在前面论述中已表明停车收费政策可以很好地缓解时段拥堵路况，其拥堵现象和停车难问题得到明显改善。为验证停车收费策略在重度拥堵路况下的优化效果，以上述数据为基础，保持各时段初始配送车辆数不变，通过增加私家车各时段的出行数量，模拟停车收费政策在重度拥堵下的调控效果。重度拥堵路况下的停车收费前后各时段车辆总流量和配送车辆流量对比分别如图4和图5所示。

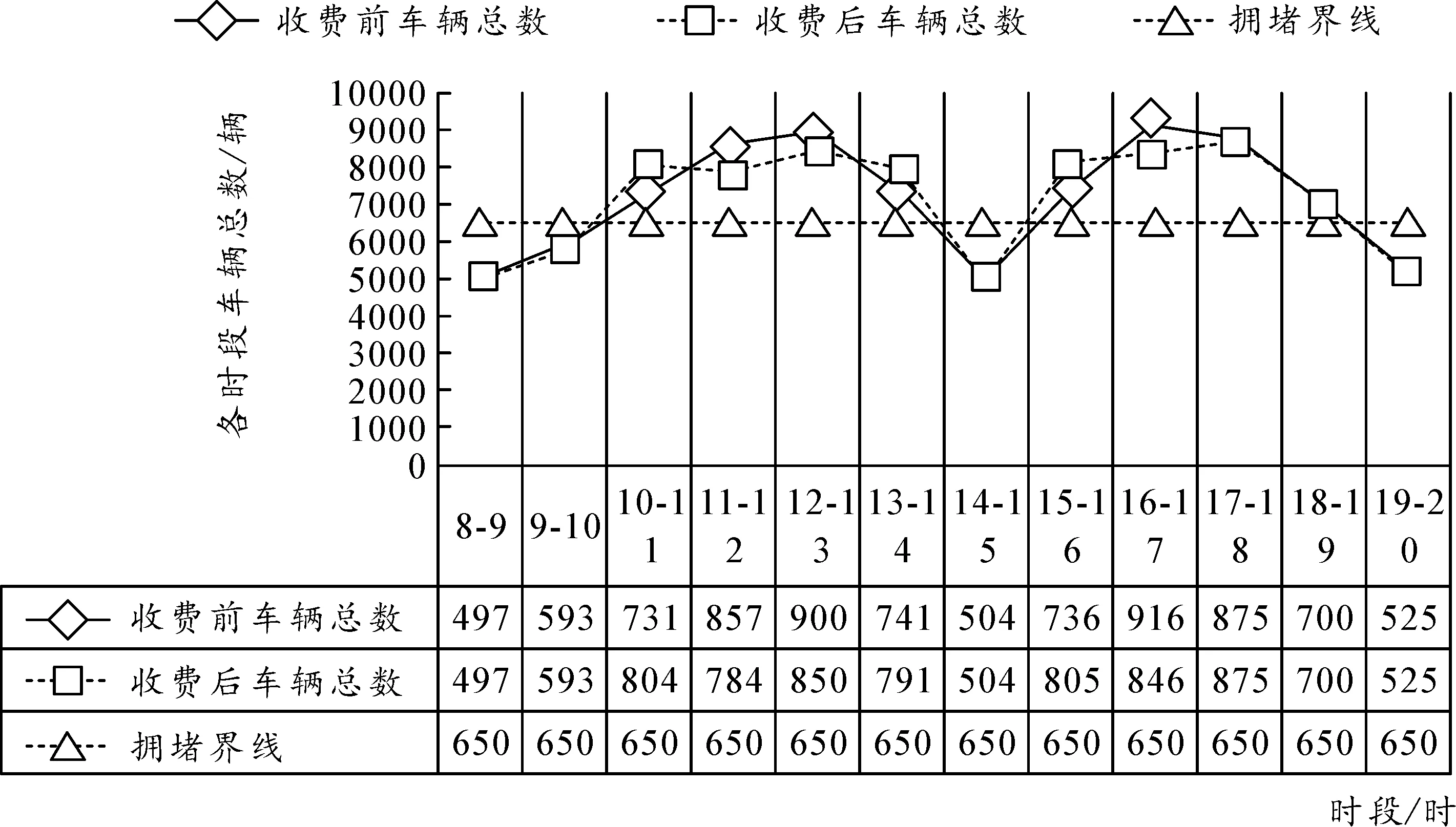
图4 停车收费前后各时段车辆总流量对比示意图

图5 停车收费前后配送车辆流量对比示意图

从图4和图5可以看出，在严重拥堵路段下，时变停车收费措施可以调控配送车辆的出行时间，停车问题依然可以得到明显的改善。但是相比于停车难问题，拥堵问题却不能得到有效的改善，因为调节配送车辆的出行时间，只能稍微降低车辆出行数量的峰值，而城市道路在大部分时间段内仍然处于极度拥堵状态，严重拥堵路段下时变停车收费政策并不能缓解城市道路的拥堵难题。因此，笔者认为缓解城市道路的严重拥堵问题，不仅需要调控城市日间配送车辆，也需要对其他车辆的出行方式和出行需求进行一定程度上的调控。

(四) 时变停车收费强度的灵敏度分析

通过上述分析可知，配送车辆会在时变停车收费措施的调控下适当改变其出行时间，并且在不考虑需求变动的情况下，拥堵时段停车收费价格越高，对车辆量的调控力度也越大，相应的社会效益损失也就越小。但是考虑到出行公平问题，配送车辆停车收费不能超过车辆出行的接受范围。为选择合适的停车收费上限，本文考察了停车收费强度对拥堵及停车数量调控的灵敏度，如图6所示。

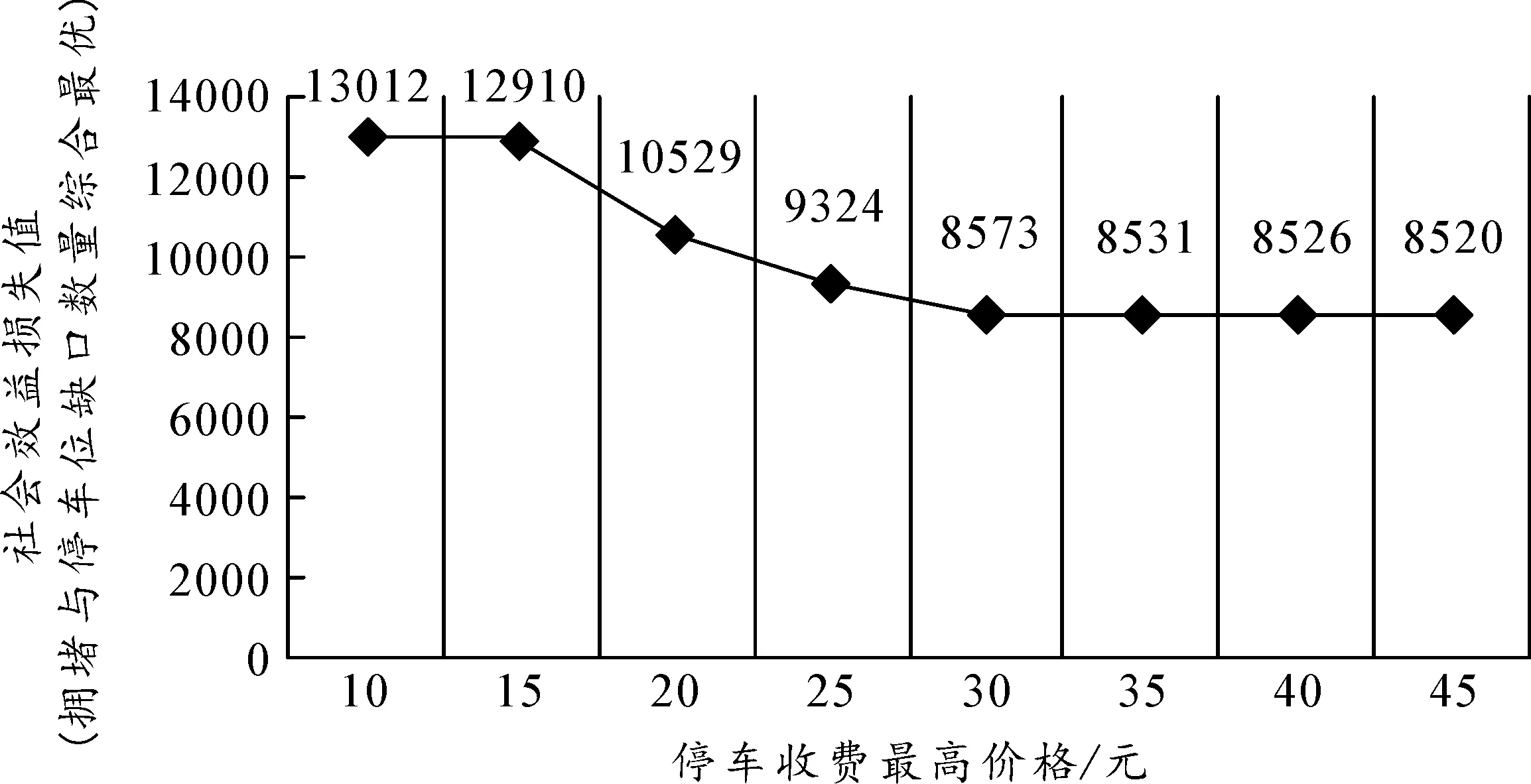
图6 停车收费强度与社会效益损失值关系示意图

从图6可以看出，随着停车收费强度的增加，平均拥堵时间和停车缺口的数量降低。当停车收费上限为30元时，日间平均拥堵程度和停车位缺口已趋于平衡，因此停车收费价格理论上不应高于30元，交通部门可以根据实际情况决策。

五、总结与展望

针对日益严峻的城市道路拥堵、停车难问题，本文首次将配送车辆停车收费措施引入到城市配送车辆问题，并以社会效益损失值最小，即日间车辆平均拥堵程度最低和配送车辆停车位缺口数量最小为目标，根据随机用户均衡理论构建了基于城市道路拥堵的物流配送车辆停车收费定价双层规划模型，缓解了早高峰和晚高峰期间的道路拥堵与停车难问题。针对模型的NP难特性，本文提出一种基于嵌入F-W迭代法的遗传算法求解该模型。最后，通过不同路况下的算例验证了模型及算法的有效性，并给出了收费价格与拥堵和停车数量的关系，为交通部门制定停车收费政策提供了辅助建议。

在后续研究中，将进一步结合交通大数据，充分考虑道路状况动态变化以及车辆在停车收费政策下的出行需求变化问题，并进一步改进嵌入F-W迭代法的遗传算法，以提高其求解效率。

[1]CHOW J Y J,YANG C H,REGAN A C.State-of-the art of freight forecast modeling:lessons learned and the road ahead[J].Transportation,2010,37(6):1011-1030.

[2]YOU S I,CHOW J Y J,RITCHIE S G.Inverse vehicle routing for activity-based urban freight forecast modeling and city logistics[J].Transportmetrica A Transport Science,2016,12(7):650-673.

[3]JALLER M,HOLGOIN-VERAS J,HODGE S D.Parking in the city:challenges forfreight traffic[J].Transportation Research Record:Journal of the Transportation Research Board,2013,2379:46-56.

[4]EDWARD C,STEF P.Regulation on-street parking[J].Regional Science & Urban Economics,2006,36(1):29-48.

[5]OTTOSSEN D,CHEN C,WANG T,et al.The sensitivity of on-street parking demand in response to price charges:a case study in Seattle,WA[J].Transport Policy,2013,25:222-232.

[6]GREGORY P,DONALD S.Getting the prices right:an evaluation of pricing parking by demand in SanFrancisco[J].Journal of the American Planning Association,2013,79(1):67-81.

[7]KEPAPTSOGLOU K,KARLAFTIS M G,ZONGZHI L I.Optimizing pricing policies in park-and-ride facilities:amodel and decision support system with application[J].Journal of Transportation Systems Engineering & Information Technology,2010,10(5):53-65.

[8]FENG H H,ZHU C K.Model of curb parking pricing in urban center district of China[J].Journal of Transportation Systems Engineering & Information Technology,2008,8(5):129-135.

[9]王健,洪麟琳,何建平.基于可变泊位容量的停车收费定价模型研究[J].武汉理工大学学报(交通科学与工程版),2013(3):517-520.

[10]张华歆,周溪召.多模式交通网络的拥挤道路收费双层规划模型[J].系统管理学报,2005(6):546-551.

[11]魏波,马耀兰.随机平衡配流与次优拥挤收费的双层规划模型构建与求解[J].统计与决策,2015(2):48-51.

[12]杨文娟,郭仁拥,李琦.基于随机用户均衡的交通配流演化动态系统模型[J].系统工程理论与实践,2015(12):3192-3200.

[13]ZHAO L,PENG Z R,YANG F,et al.A bid-rent land-use adaptation model for mitigating road network vulnerability and traffic emissions[J].International Journal of Environmental Science and Technology,2014,11(8):2359-2368.

[14]LIU Y,YANG Z S,LIU F.A traffic control strategy for sensitive junction under disaster conditions[J].Advanced Materials Research,2011,255-260:4065-4069.

[15]曾庆成,陈文浩,黄玲.集装箱码头集卡拥堵收费模型与算法[J].大连理工大学学报,2015(1):73-80.

[16]吕彪,蒲云,刘海旭.基于遗传算法的随机路网次优拥挤收费模型[J].计算机工程,2013(8):257-261.