1956-2015年高邮市气温和降水量变化特征研究
2018-03-16王雨斐方国华
王雨斐, 方国华, 闻 昕, 张 钰
(河海大学 水利水电学院, 江苏 南京 210098)
1 研究背景
根据IPCC第五次评估报告,全球地表持续升温,1880-2012年全球平均温度升高0.85℃(0.65~1.06℃);在北半球,1983-2012年达到近1400年来气温最高的30年[1]。中国气候变暖趋势与全球一致。近百年来中国地表增温率为0.12℃/10a,20世纪80年代中期后增温明显,最近50年增温率约为0.22℃/10a,明显高于全球同期增温率[2]。近100年和近60年全国年降水量无明显趋势性变化,但20世纪70年代后存在年代际变化[3]。不同区域应对气候变化响应存在差异。比如王珂清等[4]根据170多个气象观测站数据分析了淮河流域气温和降水的时空变化趋势,结果表明全流域增温显著,年平均气温气候倾向率为0.21℃/10a,空间上东部增幅高于西部,年降水量变化趋势未通过统计检验,但2000年之后明显增加。夏露等[5]引入气候趋势系数进行了气温、降水与时间序列的相关性的研究,结果表明江苏地区有明显变暖趋势且年降水量与年代呈正相关,空间上江南较江北气候因素变幅更大,更加暖湿。
高邮市地处江淮平原南端,位于江苏中部,隶属扬州,处在南水北调东线工程源头段,是水稻的重要产区。包云轩等[6]选取高邮作为江淮稻区的代表性测站研究了近30年气候异常对农业病虫害发生程度的影响,胡玉玲等[7]利用高邮市1953-2007年地面观测资料对极端气温与降水事件分强度等级研究其四季演变特征,并揭示出本世纪以来高级别旱涝灾害呈多发状态,自20世纪90年代开始极端气温值上升明显且高温日数增多、低温日数减少,表现为增暖趋势。总的来说现有关于高邮市气温、降水量特征的研究很少。本文采用多种统计分析方法,通过对高邮市1956-2015年气温降水这两个重要气候要素时间序列的研究,分析气候变化特征,以期为该地区及周边地区农业灌溉、病虫害防治、城市防洪减灾、能源供给提供决策支持和参考依据。
2 研究方法与资料来源
2.1 研究方法
基于对气候要素气温与降水量时间序列的研究,分析气候的变化特征,分别对气温与降水量进行趋势分析、突变检测、周期分析。采用线性回归、滑动平均、小波分解[8]考察时间序列的趋势特征,结合Mann-Kendall(M-K)趋势分析法[9-10]对其进行信度水平检验;由M-K突变检验[11]寻找突变的年份,并用滑动T检验(Moving T-Test)[12]进行验证;采用Morlet小波变换[13-15]进行多时间尺度的周期分析。
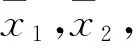
(1)
(2)
若|ti|>tα/2,则认为突变发生(α为显著性水平)。2.1.2Mann-Kendall检验M-K检验是非参数检验的一种,它不对变量的分布作严格假定,广泛应用于水文、气候、化学、矿物成分检验等方面。序列Xi=(x1,x2,…,xn),趋势检验的M-K统计量为:
(3)
其中:
(4)
(5)
Var(s)=n(n-1)(2n+5)/18
(6)
式中:UFk统计量符合标准正态分布,若存在|-UFk|>Uα/2(α为显著性水平),表明在该时段内序列变化趋势显著。
将时间序列X按逆序排序,再按式(3)进行计算,同时令UBk=-UFk(k=n,n-1,…,1。),通过对比统计序列UFk和UBk。可进一步识别序列X的趋势和突变点。将UFk、UBk。曲线以及两条显著性水平线绘制在同一张图上,若UFk为正值,表明序列呈上升趋势;UFk为负值,表明序列呈下降趋势;若UFk和UBk两条曲线相交于两条显著性水平线之间的区域,则交点对应的时刻即为突变发生的时间。
2.1.3 小波分析 小波分析能够同时从时域和频域揭示时间序列的局部特性,适合于研究具有多时间尺度变化特性的非平稳信号。各种气象因子、水文过程都可以看作是随时间有周期性变化的信号。本文利用Morlet小波对高邮市年平均气温和年降水时间序列进行多时间尺度特性分析,把时间序列分解为不同尺度(低频和高频成分)的小波系数和尺度系数,再根据时间序列低频和高频成分,分析序列的变化趋势和周期组成。
(1)趋势分析:大于实测序列长度的周期成分可以表征趋势,因此时间序列在不同尺度下的变化趋势可以用该尺度下的低频成分来表示。水文序列的低频系数可由小波分解得到,最后通过低频系数的变化过程便可识别出该尺度下的变化趋势。
(2)周期分析:Morlet小波是一种复数小波,其实部等值线图可以反映时间序列不同时间尺度的周期变化及其在时间域中的分布,其系数模等值线图可以反映不同时间尺度变化周期所对应的能量密度在时间域中的分布,其方差图可以反映时间序列的波动能量随时间尺度的分布情况,因此能够确定时间序列中存在的主要时间尺度,即主周期。
2.2 资料来源
本文所用高邮市1956-2015年近60年逐月平均气温、降水量以及年平均气温、降水量资料均来自中国气象科学数据共享服务网中的高邮市气象台站,数据来源可靠度高,并通过一致性检验。
3 气温、降水变化特征分析
3.1 趋势分析
对高邮站1956-2015年的气温、降水资料采用线性倾向估计、5年滑动平均、小波分解多种统计方法分析气候变化趋势特征,再由Mann-Kendall趋势检验对其进行置信水平分析。
3.1.1 气温趋势特征分析 高邮市1956-2015年气温变化序列及5年滑动平均变化过程见图1。

图1 年平均气温特征趋势线
整体而言,高邮市近60年气温上升趋势显著,线性递增率约为0.30℃/10a。由图1可知:(1)在研究时段内,1956-1961年气温有一个上升阶段,之后一直平稳波动,1968-1972年经历小幅下降过程,从1984年开始气温明显波动上升,至2007年达到最高温16.6℃,2007-2015年气温略有下降。(2)由5年滑动平均线可看出,自20世纪90年代中期以来年平均气温明显高于多年平均水平15.1℃,1994年以前年平均气温基本低于多年平均水平。
对气温时间序列进行小波多层分解,逐渐滤除高频成分可获得代表时间序列发展趋势的低频分量。本文通过MATLAB实现小波类型db3,分解尺度为5的小波分解。以近似分量a3为例(图2),可以看出年平均气温在20世纪50年代后期有小幅上升,之后呈小幅下降趋势,总体而言1983年以前变化趋势较为平缓;1983以后增温趋势显著,至1998年气温稳定在近60年较高位处变化。

图2 气温小波分解图(a3)
通过M-K趋势分析法对高邮市年平均气温趋势作显著性检验,其中M-K趋势指标U=5.0513,|U|>Uα/2,由此可知高邮市近60年年平均气温上升明显,通过了α= 0.01显著性检验。
3.1.2 降水趋势特征分析 整体而言,高邮市近60年降水量变幅不明显,略有上升,线性递增率约为2.2mm/10a。由图3可知:(1) 除个别年份外,高邮市年降水量平稳波动,无明显上升或下降趋势。1978年年降水量是近60年最小,为482.1mm;1991年年降水量达到近60年最大,为1823.9mm;极值比为3.8。(2)由5年滑动平均线可看出,高邮市年降水量曲线围绕多年平均年降水量线上下波动,无明显的上升或下降趋势。
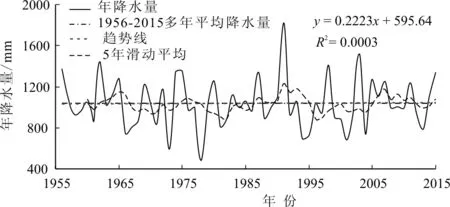
图3 年降水量特征趋势线
对降水量时间序列进行小波多层分解,逐渐滤除高频成分可获得代表年降水量时间序列发展趋势的低频分量。以近似分量a3为例(图4),可以看出高邮市年降水量近60年大致经历了3次明显波动,具体来说20世纪50年代中期至60年代中期总体呈下降趋势,60年代后期至70年代中期上升,之后下降,80年代中期开始呈上升趋势,进入90年代后下降,90年代末开始呈上升趋势。

图4 年降水量小波分解图(a3)
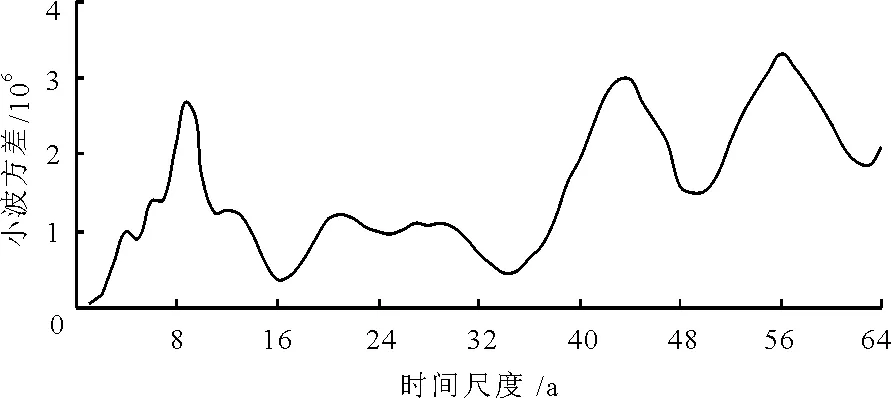
通过M-K趋势分析法对高邮市年降水量趋势作显著性分析,其中M-K趋势指标U=-0.1403,|U| 结合滑动T检验与Mann-Kendall突变检测同时对1956-2015年高邮市年平均气温和年降水量进行突变检验,以获取突变年份,置信水平取95%。3.2.1 气温序列突变检测 如图5所示,当子序列长度n=10时,由滑动T检验可大致判断突变发生在两个时段,分别为1967-1970年和1986-2003年(不包含端点)。 图5 气温滑动t检验统计量曲线(n=10) 如图6所示,当子序列长度n=7时,可大致判断突变发生于两个时段,分别是1965-1970年和1986-1999年,这两个时段基准点前后子序列均值存在明显差异。 图6 气温滑动t检验统计量曲线(n=7) 根据M-K突变检测(图7),年平均气温的正序列曲线UF和反序列曲线UB在1998年交于0.05显著性水平线范围内,符合滑动T检验判断的突变时间区域,因此1998年为突变点。同时由UF曲线看出,自20世纪90年代中期开始,UF统计量由负变正,表明气温时间序列进入上升阶段,进入21世纪以来UF统计量超过0.05显著性水平值,说明2000年后增温显著。综合上述分析,高邮市年平均气温在1998年左右发生转暖突变,之后明显上升。 图7 气温Mann-Kendall检验统计量曲线 3.2.2 降水序列突变检测 对高邮市近60年年降水量进行滑动T检验。为避免由于子序列长度选择的主观性引起突变点偏移,选取多个子序列长度进行计算并比较,且一般基准点前后两个子序列选取相同长度,即n=n1=n2。结果表明,当n=7、9、10、12时,均未检测到前后两个子序列均值差异超过0.05显著性水平,即未发现可能的突变时间区域。图8为子序列长度为10时的突变检测情况,统计量曲线保持在信度水平线内波动,可以看出无明显突变特征。 图8 1966-2006年降水量滑动t检验统计量曲线(n=10) 结合M-K突变检验分析,UB和UF统计量曲线波动稳定均未超过临界线,表明无明显上升或下降趋势,不存在突变时间区域(图9)。两曲线交点所对应年份的t统计量均未通过0.05显著性水平检验,因此交点处并非突变年份。综合上述分析,高邮市近60年年降水量未发生突变。 通过Morlet小波进行高邮市近60年气温、降水时间序列的周期性分析。小波系数实部等值线图能够反映气候要素在整个分析时域上不同时间尺度下的周期变化规律;从小波系数模等值线图可以看出随时间尺度周期震荡的强弱变化,小波系数模值越大,则该尺度下周期能量越大;小波方差图反映不同时间尺度上波动能量的分布,可以看出包含在时间序列中的主周期,进一步验证小波系数模等值线图。 图9 降水量Mann-Kendall检验统计量曲线 3.3.1 气温序列周期分析 高邮市年平均气温的Morlet小波系数实部等值线如图10。图10中小波系数正值用实线标出,表征气温偏高,小波系数负值用虚线标出,表征气温偏低。可以发现高邮市年平均气温的变化周期主要存在55、43、36、27a左右这4类时间尺度,其中55a左右的时间尺度周期在整个研究时段上表现稳定,其震荡最明显存在明显的震荡中心,具有全域性;43a时间尺度主要存在于20世纪70年代至20世纪末;36a左右的时间尺度主要存在于70年代中期以前及2000年以后;27a左右的时间尺度在20世纪50年代中期至70年代中期较明显。 图10 气温小波系数实部等值线图 由Morlet小波系数模等值线图(图11)可知,55a左右的特征时间尺度对应的小波系数模值最大,震荡能量最强、周期最显著,其余3类时间尺度43、36、27a在研究时段初期和末期表现为能量较弱的震荡。 气温的小波方差图(图12)表明高邮市气温时间序列的波动能量随尺度变化过程中存在一个明显的峰值,对应55a的时间尺度,表明该尺度下周期震荡最为强烈,进一步表明年平均气温变化存在55a的主周期。 图11 气温小波系数模等值线图 图12 气温的小波方差图 3.3.2 降水序列周期分析 高邮市年降水量的Morlet小波系数实部等值线如图13。图中小波系数正值用实线标出,表征降水量偏多期,小波系数负值用虚线标出,表征降水量偏少期。 可以发现高邮市年降水量周期变化存在56、43、20~30、9a左右这4类较明显的时间尺度。总的来说,这4类时间尺度的周期变化在整个时域中表现稳定、震荡明显。 图13 年降水量小波系数实部等值线图 由Morlet小波系数模等值线图(图14)可知,56、43、9a左右的特征时间尺度对应的小波系数模值较大,周期较为显著,其中56a左右的时间尺度的震荡能量最强。20~30a时间尺度周期震荡能量相对较弱。 图14 年降水量小波系数模等值线图 年降水量的小波方差图(图15)表明高邮市近60年年降水量时间序列的波动能量随尺度变化过程中存在5个较明显的峰值,分别为9、21、29、43、56a,其中56a左右的时间尺度对应峰值最大,该尺度下周期震荡最强,为高邮市年降水量变化的第一主周期,43和9a分别对应第二、第三周期。 图15 年降水量的小波方差图 基于高邮市1956-2015年气温和降水量资料,通过线性回归、滑动平均、小波分解分析气温与降水量的变化趋势;采用滑动T检验结合Mann-Kendall检验的方法检测突变年份;根据Morlet小波变换掌握气温及降水量的周期变化规律,可得出以下结论: (1)高邮市近60年年平均气温以0.01的显著性水平呈明显上升趋势,平均增温率达0.30℃/10a,年平均气温在1998年左右发生突变,存在55a左右的主周期。 (2)高邮市近60年年降水量变幅不明显,有微弱升高,上升倾向率为2.2mm/10a,近60年未发生突变,年降水量存在56a左右的第一主周期。 (3)从周期性来看,近60年高邮市年平均气温存在一个明显的主周期55a;年降水量的第一主周期为56a,第二、三主周期分别为43、9a;显然年平均气温与年降水量主周期波动规律具有相似性,时间序列的演变过程中存在一定联系。 [1] 沈永平,王国亚.IPCC第一工作组第五次评估报告对全球气候变化认知的最新科学要点[J].冰川冻土,2013,35(5):1068-1076. [2] 丁一汇,任国玉,石广玉,等.气候变化国家评估报告(I):中国气候变化的历史和未来趋势[J].气候变化研究进展,2006,2(1):3-8+50. [3] 丁一汇,王会军.近百年中国气候变化科学问题的新认识[J].科学通报,2016,61(10):1029-1041. [4] 王珂清,曾 燕,谢志清,等. 1961-2008年淮河流域气温和降水变化趋势[J].气象科学,2012,32(6):671-677.[5] 夏 露,张 强,孙 宁,等. 1960-2012年江苏省气候变化特征[J].冰川冻土,2015,37(6) :1480-1489. [6] 包云轩,蒋 蓉,谢晓金,等.近30年气候异常对江苏省褐飞虱灾变性迁入的影响[J].生态学报,2014,34(23):7078-7092. [7] 胡玉玲,熊 伟,康建鹏,等.高邮市55年来极端天气事件的变化特征[C]//淮河流域综合治理与开发科技论坛论文集,中国气象学会,2010. [8] 潘雅婧,王仰麟,彭 建,等.基于小波与R/S方法的汉江中下游流域降水量时间序列分析[J].地理研究,2012,31(5):811-820. [9] 康淑媛,张 勃,柳景峰,等.基于Mann-Kendall法的张掖市降水量时空分布规律分析[J].资源科学,2009,31(3):501-508. [10]NOVOTNYEV,STEFANHG.StreamflowinMinnesota:Indicatorofclimatechange[J].JournalofHydrology, 2007, 334(3-4):319-333. [11] 符淙斌,王 强.气候突变的定义和检测方法[J].大气科学,1992,16(4):482-493.[12] 雷红富,谢 平,陈广才,等.水文序列变异点检验方法的性能比较分析[J].水电能源科学,2007,25(4):36-40.[13] 张 钰,孙 涛,方国华,等.新乡市城区近64年气温和降水量特征分析[J].水资源与水工程学报,2017,28(1): 94-99.[14] 邵晓梅,许月卿,严昌荣.黄河流域降水序列变化的小波分析[J].北京大学学报(自然科学版),2006,42(4):503-509.[15] 赵利红.水文时间序列周期分析方法的研究[D].南京:河海大学,2007.3.2 突变检测




3.3 周期分析

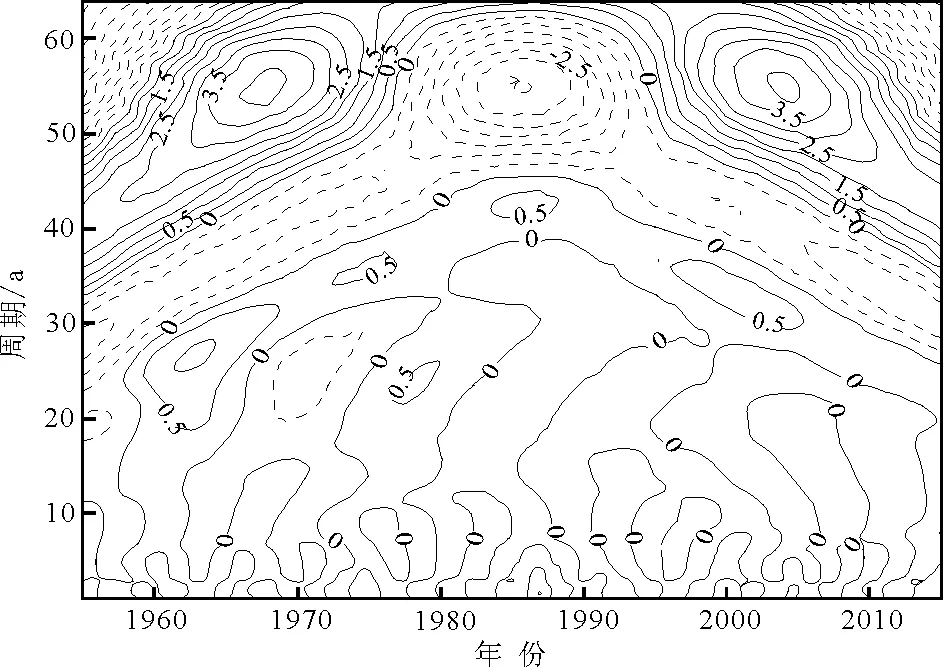

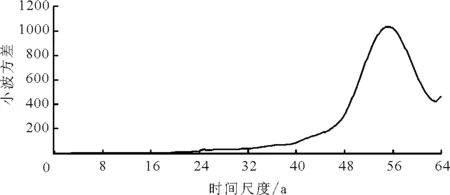


4 结 论
