基于模型参考自适应的电动车用内置式永磁同步电机电感参数辨识技术研究

宛 野，袁飞雄，高 跃



基于模型参考自适应的电动车用内置式永磁同步电机电感参数辨识技术研究

宛 野，袁飞雄，高 跃

（武汉船用电力推进装置研究所，武汉 430064）

内置式永磁同步电机（IPMSM）由于其优良的转矩特性和宽广的调速范围而广泛运用于电动汽车电驱系统。与表贴式永磁同步电机(SMPSM)不同，IPMSM转子具有强烈的凸极效应。因此其控制方式相较表贴式更为复杂，需要更加精确的电机数学模型。但是由于饱和效应和交叉耦合，电感参数会随运行工况变化而发生变化，从而影响系统控制精度，所以能够实时掌握内置式永磁同步电机电感参数是非常重要的。本文采用模型参考自适应算法（MRAS）实现IPMSM电感参数在线辨识，运用RungeKutta离散化方法建立可调模型，依据Popov超稳定性定理推导出自适应律。仿真结果表明，采用MRAS的在线参数辨识算法可以准确、实时地辨识出IPMSM的交、直轴电感。

电动汽车 内置式 参数辨识 模型参考自适应

0 引言

在低碳经济的市场环境下，新能源汽车成为全球节能与环保领域里备受推崇的新兴产业，汽车的电动化更是备受关注，电力驱动系统更是电动汽车的核心部件。内置式永磁同步电机（IPMSM）首先由于其永磁体埋在转子内部，因此具有更高的机械强度，适应更高的转速；其次内置式永磁同步电机由于其较大的凸极率而产生的磁阻转矩可以提高恒转矩性能和拓宽恒功率范围。内置式永磁同步电机由于上述优势已成为当前电动汽车用电驱系统中应用最多的电机[1]。但是正是由于内置式永磁同步电机不同的交直轴电感产生的磁阻特性导致其控制方式比表贴式永磁同步电机要更加复杂。因此需要更加精确的数学模型对其进行控制。由于内置式永磁同步电机具有磁饱和和磁路交叉耦合的特点，因此不同工况下其电感参数会产生变化，从而影响电机的控制精度。为了保证控制精度，提高电机性能，需要在工程实际中运用算法对电感参数进行实时辨识。

目前参数辨识主要的分类方式为离线辨识和在线辨识，本文主要讨论的方式为在线辨识方式因此暂不讨论离线辨识方式。目前主要的在线辨识方式有最小二乘法、模型参考自适应、卡尔曼滤波和人工智能算法。最小二乘法算法计算原理简单、算法易于实现，但是其辨识精度不高易受干扰。卡尔曼滤波可得到精确地辨识结果，有效的避免噪声问题，但当同时辨识多个参数时，就需要对很多矩阵和矢量同时进行运算，运算过程比较复杂，且协方差矩阵的参数值要不断的进行调试，使得难度比较高。相比较而言模型参考自适应算法原理简单、辨识精确并且能快速收敛。

本文对基于MTPA控制的电动汽车电驱系统进行了仿真，推导了基于Popov超稳定性定理的模型参考自适应参数辨识算法，并运用该算法在仿真中实现了内置式永磁同步电机轻载至额定工况电感参数的快速准确辨识。

1 IPMSM数学模型及MTPA控制理论

1.1 内置式永磁同步电机线性数学模型

三相永磁同步电机是一个多变量、非线性、强耦合的复杂系统，为了便于分析往往会做一些假设：

1）定子绕组三相对称并且完全相同，各绕组轴线相差120°。

2）忽略磁路饱和、磁滞和涡流的影响，磁路是线性的，可以用叠加原理进行分析，转子上没有阻尼绕组。

3）当定子绕组电流为三相对称正弦波电流时，气隙空间中只产生正弦波分布的磁通势，无高次谐波分布。

4）永磁体在气隙空间中产生的磁通势为正弦分布，无高次谐波，也就定子在空载时电动势为正弦波[1]。

基于上述假设，可以得到在三相静止坐标系中的定子电压方程。通过PARK变换可以得到同步旋转坐标系下内置式永磁同步电机的定子电压方程：

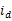
电磁转矩方程

式中的第一项是由永磁体的励磁磁场与定子电流的相互作用而产生的电磁转矩，第二项是由电机转子的凸极效应所造成的磁阻转矩，该转矩产生的原因是因为内置式永磁同步电机的交、直轴电感不等。该转矩的存在可有效的提高电机的转矩输出能力，扩大电机恒功率区域的运行范围。

1.2 IPMSM的MTPA控制及参数变化

电机输出性能的好坏除了电机本身性能方面的原因外，主要还是取决于电机控制方法。根据电机的运行特点，一般将电机的运行区域分为恒转矩区和恒功率区。对于内置式永磁同步电机而言为了更好地利用其凸极效应，充分发挥电机的固有特性，提高电机效率，一般在恒转矩区采用单位电流最大转矩控制（MTPA），在恒功率区采用弱磁控制。

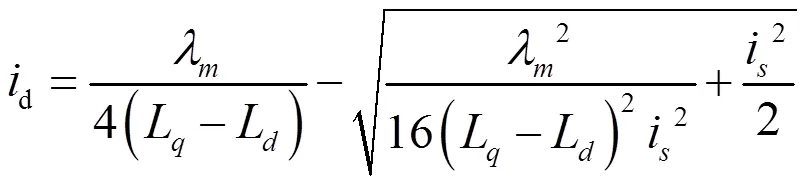
但是由于磁路饱和和交叉耦合现象，会导致交直轴电感在电机实际运行过程中产生非线性的变化，在使用参数计算的MTPA控制算法中，变化的电感参数必然导致电流计算不准确从而影响控制效果[2]。因此找到一种能够在电机运行时实时获取电感参数的算法对于提高电机控制效果是很有十分有利的。

2 模型参考自适应算法

模型参考自适应（MRAS）算法最早是由美国麻省理工学院的怀特教授在50年代末期提出的，其初衷是为了解决飞行器自动仪的控制问题。其基本原理为当受控对象动态特性参数发生大的不可预测的变化时，为了构造高性能的控制系统或者得到受控对象的参数，我们可以预先构造一理想的满足预期性能的参考模型，控制参考模型和受控系统具有完全相同的输入，比较参考模型和受控系统的输出，利用他们输出的误差构造自适应机构，由自适应机构产生的附加控制作用去修改受控系统参数，或作为控制信号作用于受控系统，直到两系统的误差达到极小值，则此时整个系统达到自适应，也可认为受控对象与参考模型参数完全相同从而达到参数辨识的目的。MRAS算法的基本结构图如图1所示。

图1 模型参考自适应系统基本结构图

结合图1我们可以分析出MRAS在永磁同步电机参数辨识技术中的应用方式，可以设定实际永磁同步电机驱动系统为参考模型，并根据内置式永磁同步电机的定子电流状态方程建立的数学式永磁同步电机电流状态方程建立可调模型。当电机运行时，保证两个模型除待辨识量外的所有参数相同，然后对其输出值进行比较，由于辨识对象实际值与估计值的误差，导致两个模型输出信号的误差，然后将该误差送到自适应律模块中，自适应模块的输出值再用来修改可调模型的估计值，经过一段时间的调节，使两个模型的输出误差趋近与0，此时可认为自适应模块的输出值为待辨识参数的实际值。

模型参考自适应算法的关键在于自适应律的确定。自适应率的确定方法一般可以分为3种：第1种方法是基于李亚普诺夫直接法 (Lyapunov)确定；第2种方法是基于局部参数最优化理论确定；第3种是基于波波夫超稳定性理论 (Popov)确定[2]。首先采用Lyapunov直接法设计自适应律需要寻找一个合适的Lyapunov函数，对设计者要求比较高，Lyapunov函数一旦寻找不合适整个系统难于收敛，因此本文并未采用第一种方法。其次由于自适应的本质是非线性时变的，其本身就存在稳定性的问题，因此在设计自适应规则时，要一直使其稳定，虽然局部参数最优化理论的形式以及推导比较简单，但其没有考虑到系统的稳定性，所以本文也未采用第二种方式。相较于前两种方式波波夫超稳定性理论 (Popov)较为灵活，更容易推导出合理的自适应率，因此本文通过波波夫超稳定性理论 (Popov)来确定在线辨识电机参数的自适应率。

3 基于Popov超稳定性定理的MRAS内置式永磁同步电机参数辨识算法

3.1 IPMSM参数辨识系统可调数学模型

内置式永磁同步电机定子电流模型如下式：

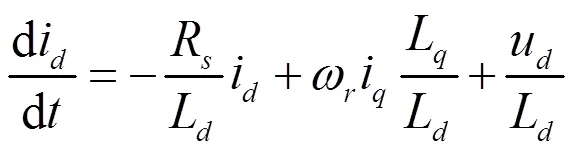
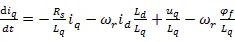
由于希望仿真时能尽量模拟真实系统，因而仿真采用离散系统。为了保证可调模型在离散系统中的精确性，同时希望把仿真步长对可调模型的影响降到最低，因此采取四阶的RungeKutta方法对定子电流的状态方程进行离散。

其中一阶斜率为：

其中二阶斜率为：

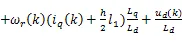
其中三阶斜率为：

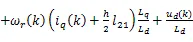
其中四阶斜率为：

3.2 采用Popov超稳定性定理确定自适应律

将式(8)和式(9)可改写为如下矩阵形式：

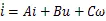
同理可以将可调模型简化为：

则参考模型和可调的误差表示为:

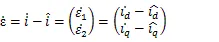
通过变形可将误差方程变换成典型的反馈系统：

令

可将式(26)表示为框图形式如图2所示。根据Popov超稳定性原理，若要使这个反馈

系统保持稳定，那么其中非线性环节应满足下述公式。

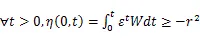
其中为一个有限正数。将前文求得的和带入到式(25)中可得：

将上式展开可得：

将式(29)可分解为三个式子，如下所示：

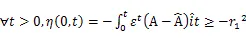
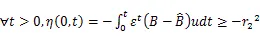
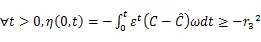
由Popov超稳定原理可知，只需式(30)至式(32)都成立，则此非线性反馈系统保持稳定。继而可以通过式(30)至式(32)推导出自适应律。通过对上述三式的分析发现其中式(31)不含交直轴电感耦合项，因此可以通过式(31)推导出交直轴电感辨识的自适应律。可将式(31)转化成下式：

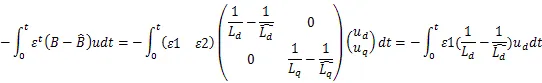
再将式(31)分解为下述两式：

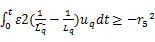
先只分析直轴电感辨识的自适应律，交轴自适应律推导过程类似。将式(36)代入式(34)中可得：

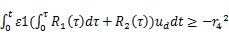
将上式进行化简可得：

证明式(39)成立可以借助式(41)：

综上所述式(36)可以改写成如下比例积分形式：

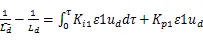
同理可得式37)也可改写成如下比例积分形式：

式(42)和式(43)即为通过Popov超稳定原理确定的自适应律。则可得整个电感参数辨识系统中，自适应律为由定子电流误差构成输入项的PI调节器。

4 辨识算法仿真分析及结果

本文仿真采用的电机原型为武汉船用电力推进装置研究所某电动车电驱系统项目中的内置式永磁同步电机。首先基于MATLAB搭建采用MTPA控制的电动汽车电驱系统仿真模型，其中电机模型和控制算法运用level-2 MATLAB S-Function模块进行编写。

仿真模型空载升速电流和转速波形图，以及额定转速加载电流和转速波形图如图3-6所示。

图3 空载升速电流波形

图4 空载升速转速波形

从图可以看出，仿真时无论空载升速还是额定转速加载转速和电流都能够迅速跟踪，表明此控制系统仿真性能优良，具备进行参数辨识的条件。

在仿真中参数辨识模块主要分为可调模块和自适应模块。整个参数辨识模块如图7所示。

图5 额定转速加载电流波形

图6 额定转速加载转速波形

图7 参数辨识模块

图8 负载为20Nm交、直轴电参数辨识波形

图示中虚线为电感实际值，实线为电感辨识值，每张图中上方为直轴电感辨识波形，下方为交轴电感辨识波形。从图示波形可以看出通过该种辨识方式交、直轴电感辨识值都能迅速收敛到实际值。通过比较不同工况辨识波形的收敛情况，可以看出该种辨识算法的收敛速度会随着负载的增加即电流增加而加快，其中110 Nm的收敛速度是20 Nm时收敛速度的5倍。其次可以看出轻载时由于d轴电流比较小，导致d轴电感辨识存在一些静态误差，随着负载的增加和d轴电流的增大该偏差被消除。

图9 负载为50 Nm交、直轴电参数辨识波形

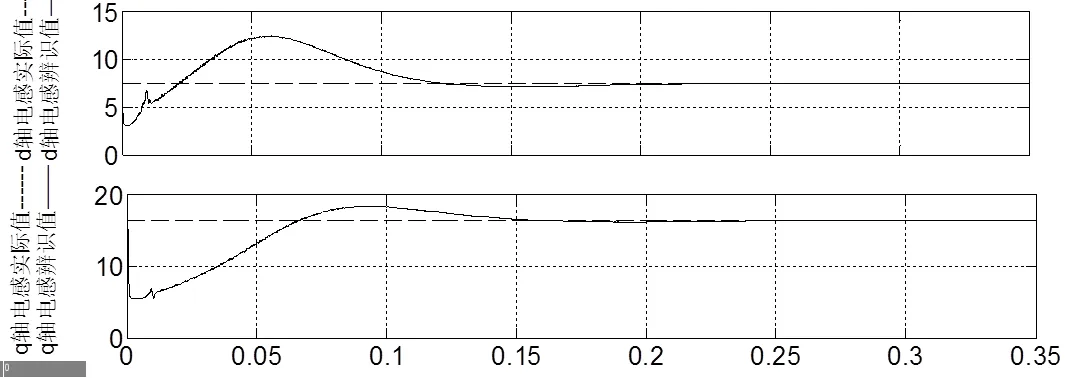
图10 负载为70 Nm交、直轴电参数辨识波形

图11 负载为110 Nm交、直轴电参数辨识波形

5 结论

本文由内置式永磁同步电机的数学模型入手，利用四阶的RungeKutta离散化方法设计了MRAS参数辨识算法的可调模型，利用Popov超稳定性原理推导出MRAS参数辨识算法的自适应律，并给出了详细的推导过程。通过仿真验证了整个MRAS参数辨识系统的稳定性，并可以在轻载、中载和额定负载等工况中完成参数辨识，且辨识值收敛迅速。可以为后续实验提供理论依据和仿真支撑。

[1] 王艾萌. 内置式永磁同步电动机的优化设计及弱磁控制研究[D]. 华北电力大学(河北),2010.

[2] 毛承雄, 涂光瑜, 文劲宇, 林湘宁. 现代控制理论[M]. 华中科技大学, 2008.

[3] 王伟华, 肖曦. 基于电感辨识的PMSM电流自适应增量预测控制[J]. 电机与控制学报, 2014, (02): 75-82.

[4] 肖曦, 许青松, 王雅婷, 史宇超. 基于遗传算法的内埋式永磁同步电机参数辨识方法[J]. 电工技术学报, 2014, (03): 21-26.

[5] 李永东. 交流电机数字控制系统[M]. 北京: 机械工业出版社, 2002.

[6] 安群涛. 一种永磁同步电动机参数的自适应在线辨识方法[J]. 电工技术学报, 2008, 6(23): 21-36．

[7] Y Shi,KSun,LHuang,YLi. Onlineidentification of permanent magnet flux based on extended Kalmanfilter for IPMSM drive with positionsensorless control[J].IEEE Transactions on Industrial Electronics, 2012, 59(11):4169-4178.

Research on Online Inductance Parameter Identification of Permanent Magnet Synchronous Motor for Electric Vehicle Based on Mod Reference Adaptive System

Yuan Ye, Yuan Feixiong, Gao Yue

(Wuhan Institute of Marine Electric Propulsion,Wuhan 430064,China)

TM313

A

1003-4862（2018）01-0019-07

2017-10-15

宛野（1992-），男，硕士。研究方向：电力电子与电力传动。