三角恒等变换之题型总结及解题策略分析

王传勇

（诸城市实验中学，山东 诸城）

三角恒等变换是解决三角函数问题的重要工具.三角恒等变换是高中数学的一个重要模块，在历年的高考中都是必考内容，同时也是很多学生学习，考试的难点.本文将三角恒等变换的一些常见题型及解决策略作了梳理，仅供参考，希望能对学生学习有所帮助.

一、公式的变形

三角公式是变换的基础，应熟练地掌握公式的顺用、逆用及变形应用.

1.化简

（1）cos（α+β）cosβ+sin（α+β）sinβ；（2）sin（α+β）cosβ-cos（α+β）sinβ

二、角的变换

在表达式中或者在已知条件和所求问题中出现较多的相异角，可以通过观察，寻找两角之间的和差、倍半、互补、互余等关系，从而应用角的变换，建立已知和结论之间的联系，使问题得以解决.

思路分析：通过寻找题目中的角α，α+β，β三者之间的关系，利用角的变换来解决.

思路分析：通过寻找题目中的角 α-β，α+β，2α 三者之间的关系，利用角的变换来解决.

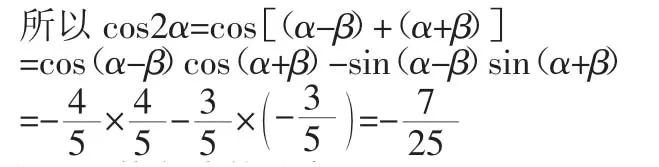
三、函数名称的改变

三角变形中，常常需要变不同函数名称为同名函数.如在三角函数中正余弦是基础，通常化切为弦，化弦为切，变异名为同名.

1.求 sin15°sin30°sin75°值.

四、常数变换，巧用“1”

在三角函数运算，求值，证明中，有时需要将常数1转化为三角函数值来代换，以达到解决问题的目的.

五、幂的变换

升降幂是三角变换时常用方法，对次数较高的三角函数式，一般采用降幂处理的方法，降幂并非绝对，有时需要升幂.

六、结构的变换

通过表达式结构特点，通过构造上的变换，从而使问题得到解决.

求 cos20°cos40°cos80°的值.

解析：根据式子结构特点，乘以并除以2sin20°.