基于HCSP和模糊熵的脑电信号分类
2018-03-16于沐涵
于沐涵,陈 峰
(南通大学 电气工程学院,江苏 南通 226019)
0 引 言
脑-机接口(brain-computer interface,BCI)[1]通过分析由运动想象产生的脑电信号就能读取人脑发出的动作指令,从而替代大脑神经与人体肌肉直接与外部设备建立连接通道,帮助肢体活动受限的人操作和控制一些辅助设备。然而由于脑电信号自身固有的非线性和非平稳性,这给脑电信号特征提取与识别带来了巨大的挑战,同时也是运动想象BCI技术一直处于实验室阶段,不能走入实际应用的主要原因[2]。
目前,研究人员已提出多种运动想象脑电信号的特征提取[3-7]方法。其中小波变换和小波包变换都是基于傅里叶变换的特征提取算法,不能在时域和频域同时具有较高的分辨率。共同空间模式提取的特征缺乏相关的频域信息,且需要大量的电极,无法应用到少通道信号中[8]。希尔伯特-黄变换在时域和频域都具有很高的分辨率,但是在EMD分解后需要人为选取IMF分量,由此可能导致重构信号混入噪声或丢失对分类有用的信息[9]。针对上述特征提取方法中的缺陷,提出了希尔伯特-黄变换与共同空间模式相结合(HCSP)的方法,结合自购实验装置EPOC,对表征手部运动想象脑电特征的C3、C4、CZ三通道分别进行经验模态分解,选取分类效果最明显的前三阶IMF及其组合构成15维的信号,应用希尔伯特变换求取瞬时幅值后,利用CSP特征提取,联合计算空间滤波器滤波后信号的AR模型参数和模糊熵[10,11]构造特征向量。针对BCI competition 2003的数据,分别采用希尔伯特-黄变换、CSP和本文提出的方法进行特征提取,再用线性分类器[12]进行分类。利用本文提出的方法其分类准确率较单独使用HHT提高了5个百分点,较单独使用CSP方法提高了15个百分点,分类结果表明此方法避免了人为选取IMF带来的不确定因素,在减少分类导联数的同时还能增加相关的频域信息,可以提取对分类更为有效的信息。
1 脑电特征提取方法
1.1 HHT简介
希尔伯特-黄变换是近年来信号处理领域的一个重大突破,自90年代末以来,已经广泛应用于地震数据、气候数据、语音信号、图像信号等数据的分析,该方法在时域和频域都具有较高的分辨率,完全适应于脑电信号这类具有非线性以及非平稳性特点的信号处理,HHT主要分为两个部分:①经验模态分解(EMD);②Hilbert谱分析[6](HSA)。
经验模态分解是希尔伯特-黄变换开始的第一步,也是整个特征提取最重要一步。利用经验模态分解可将一复杂多分量信号分解为一些简单分量之和[13],这些简单分量必须满足任意时刻上下包络线相对于时间轴对称,且其极值点数和过零点数相差最多为1,满足上述条件的分量称作固有模态函数(IMF)。
EMD的分解过程描述如下:
(1)对任一实信号x(t),确定x(t)的所有极大值点和极小值点。
(2)对所有的极值点用三次样条函数拟合成一条光滑的曲线形成信号的上下包络线,计算其均值曲线,计算x(t)和均值曲线的差值h(t)。
(3)考察差值h(t)是否满足IMF的条件。如果满足条件直接作为IMF分量,如果不满足条件,重新执行步骤(1)、步骤(2),直到满足条件为止,并作为第一个IMF分量c1(t),求得x(t)与IMF分量的差值r(t)。
(4)将差值r(t)作为原始信号重复上述的筛选,直至剩余分量为一个单调信号或者只有一个极值点为止,本文所用的停止条件:当两次筛选间的标准差SD小于0.2时即认为筛选已经结束。表达式为
(1)
在利用EMD分解得到各个IMF分量后,对每一个IMF分量做Hilbert变换即
(2)
构造解析信号Zi(t)
Zi(t)=Ci(t)+jH[Ci(t)]=ai(t)ejθi(t)
(3)
进而求得解析信号的瞬时相位和瞬时幅值
(4)
(5)
在传统的HHT的特征提取的过程中通常是选取前几阶IMF分量的叠加来进行分析,本文采用共同空间模式算法来选取对特征提取最有效的分量。
1.2 CSP简介
CSP算法是近年来应用于多通道分类的一种主流的分析方法,最初是应用于BCI系统的脑电异常检测,到后来逐步应用于运动想象脑电信号的分类中。其核心思想请参考文献[14]。设一次实验的脑电信号表示为一个N×T维的矩阵X
(6)
式中:N是采样通道数,T表示每个通道的采样点数。Xl和Xr分别是想象左右手的脑电数据。CSP运算过程如下:
(1)计算想象左右手动作的空间协方差矩阵Cl、Cr
(7)
(8)
(2)计算出所有实验的平均协方差矩阵组成混合空间协方差矩阵
(9)
对C进行特征值分解,式中Σ为特征值对角矩阵,其中UO为特征值所对应的特征向量。
(10)
(11)
(12)
(4)根据矩阵同时对角化原理:Sl、Sr应该具有相同的特征向量,且特征值矩阵的和为单位阵
Sl=UλUT
(13)
Sr=U(I-λ)UT
(14)
(5)Ul和Ur分别是特征值矩阵λ和Ι-λ中最大特征值所对应的特征向量,利用白化矩阵P构造空间滤波器Wl、Wr
(15)
(16)
(6)则原始的脑电信号经过滤波器滤波,求得特征向量Zl、Zr
Zl=Wl×X
(17)
Zr=Wr×X
(18)
(7)进一步提取出2维特征向量
(19)
Var(X)是计算X的方差。
利用矩阵对角化原理,CSP算法可实现空间滤波器寻优,利用该最优滤波器获取更明显的特征向量,但CSP算法缺乏相关的频域信息而且只有在输入导联数达到一定数量时,才能达到较佳的分类效果,这也限制了共同空间模式算法的应用,制约了BCI系统的发展。
1.3 HHT和CSP相结合的特征提取算法
本文提出一种HHT与CSP相结合的特征提取算法,首先采用EMD方法将3个导联的原始脑电信号分解为众多简单分量的叠加,提取每个通道对运动想象分类有效的IMF分量及它们的组合组成5维重构信号,可假定15个通道的脑电信号来做CSP特征提取,算法流程如图1所示。
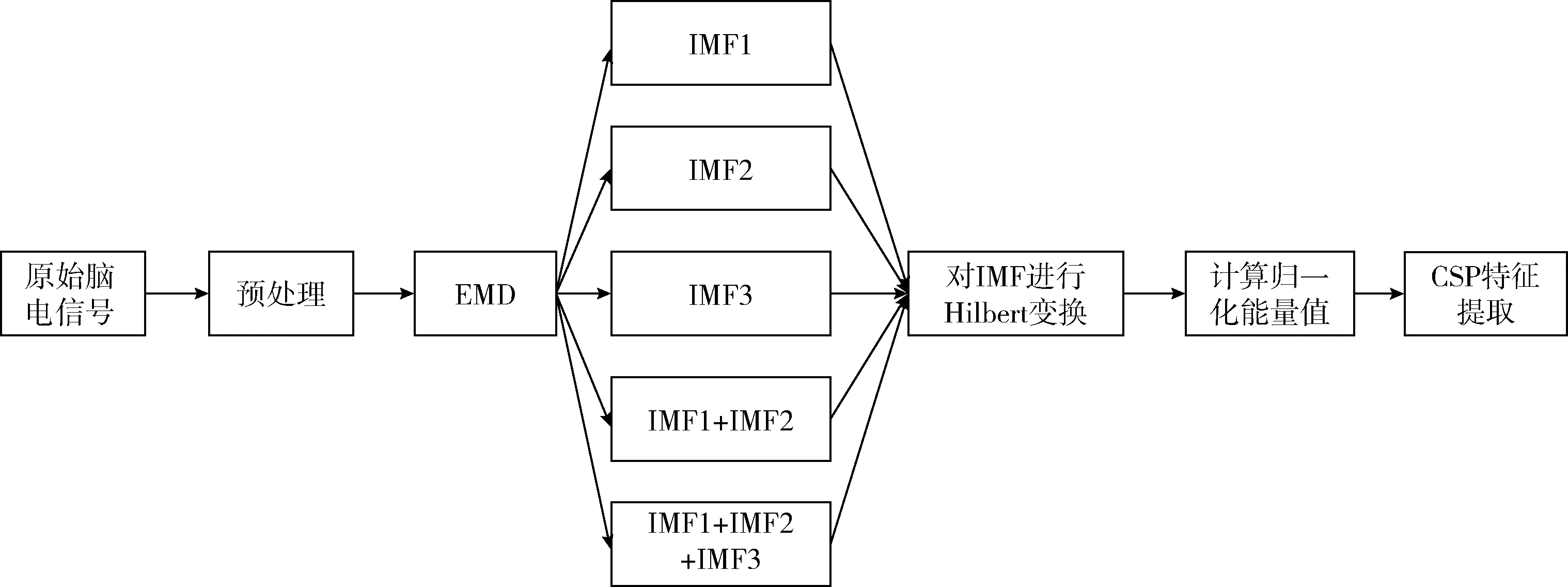
图1 特征提取算法流程
研究表明,运动想象脑电信号主要发生在8 Hz~30 Hz,本文在特征提取之前首先对原始脑电信号进行8 Hz~30 Hz的带通滤波,采用butterworth滤波器,设置通带截止频率8 Hz~30 Hz,阻带截止频率5 Hz~35 Hz,通带衰减0.5 db,阻带衰减50 db。然后对滤波后的信号进行经验模态分解,分解后的各阶IMF如图2所示。
前期研究表明,只有前三阶分量的频率范围属于运动想象的节律段,选取前三阶IMF分量及它们的组合,进行希尔伯特变换提取瞬时幅值,由于脑电特征的瞬时幅值波动较大,本文采用1S的滑动时间窗,滑动步长为一个采样点,提取平均瞬时能量并进行归一化处理来表征分类特征信息。图3是归一化后的能量随时间变化的曲线。
选择与手部运动想象最相关的3个导联(C3、CZ、C4),进行EMD分解,每个导联提取前三阶固有模态分量及前三阶分量的组合,组成一15维向量E15×T作为原始脑电信号。在运动想象信号的研究中,ERD/ERS现象并非存在于整个想象过程中。由图3可知,在4 s至7 s期间,C3、C4通道的能量差异最大,可以认为在此时间段的ERD/ERS现象最明显。本文选取此时间段内200个采样点数据(即601-800点),并对E15×200进行CSP特征提取。本文选取特征值矩阵中最大和最小特征值对应的特征向量构成空间滤波器,对E15×200进行滤波处理,滤波后的信号为Z2×200,进一步提取出2维特征向量fp。
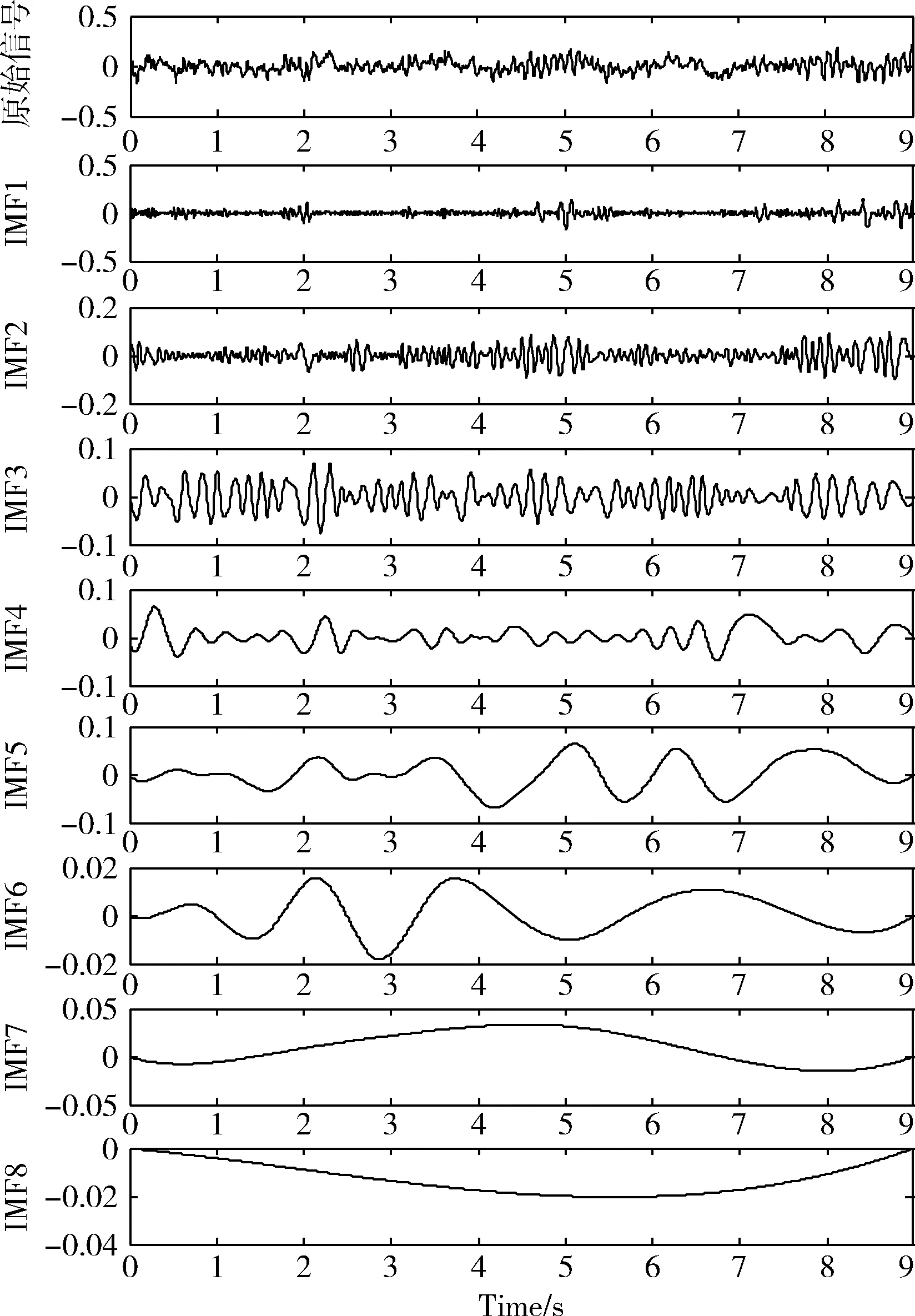
图2 脑电信号EMD后各阶IMF
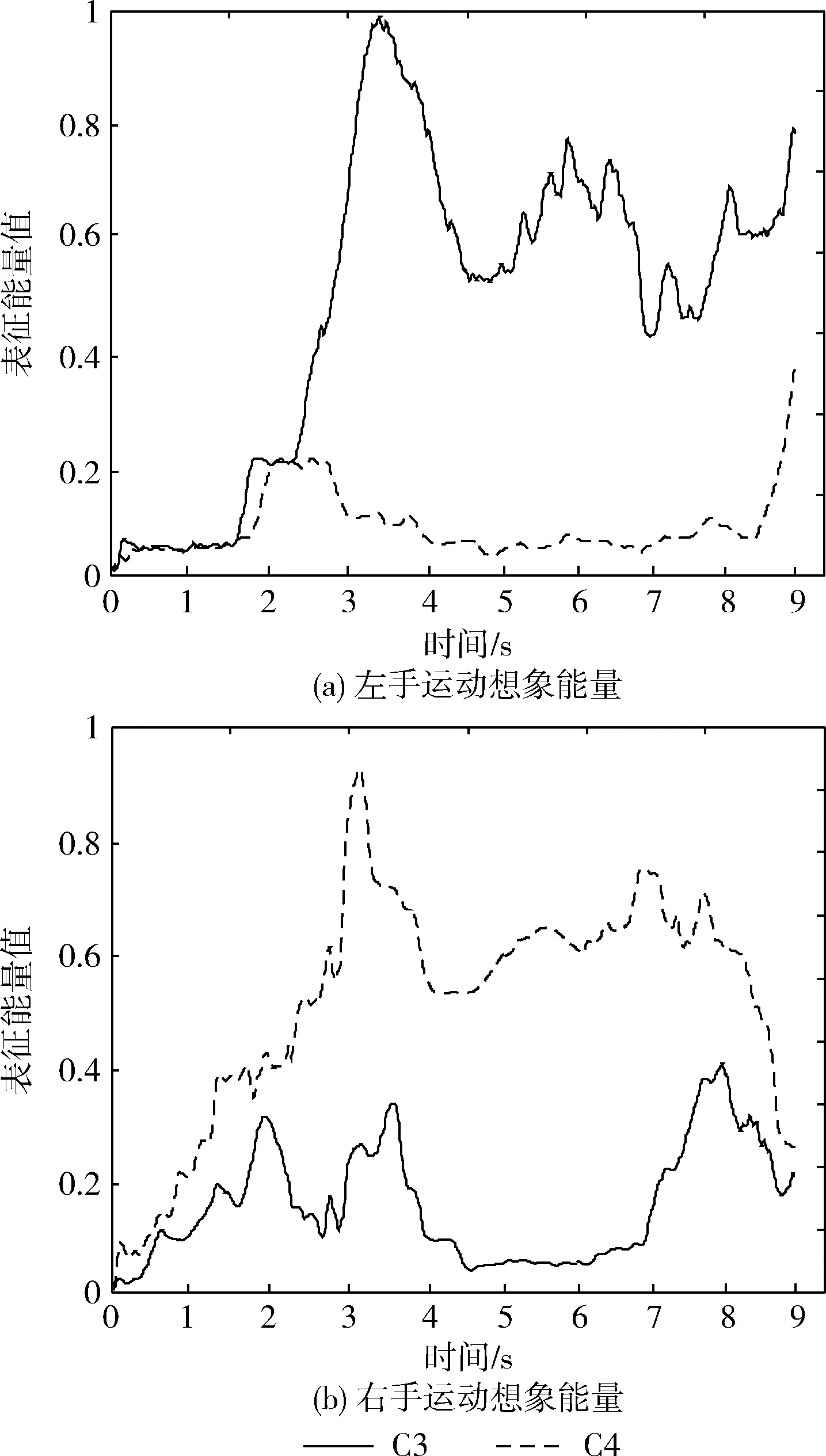
图3 左右手运动想象脑电能量曲线
1.4 AR模型特征提取
进而对经空间滤波器滤波后的信号Z2×200提取自回归(auto regressive,AR)模型参数,本文分别使用3、5、6、8、10、12、14、16阶AR模型提取AR模型参数,分别求取最后的分类准确率[6],如图4所示。
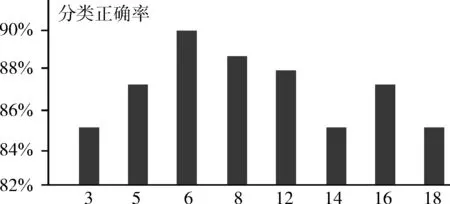
图4 各阶AR模型分类准确率
鉴于在阶次为6时对应了最大的分类准确率,本文基于Burg算法提取6阶AR模型系数组成12维的特征向量:{C3AR1,…,C3AR6,C4AR1,…,C4AR6}。
1.5 模糊熵特征提取
脑电信号是一个非线性信号,它还具有一定的非线性特征[15]。熵是一种非线性动力学参数,可以用于衡量时间序列中产生新模式概率的大小,得出脑电信号的复杂度。在对脑电信号进行非线性检测时,我们通常提取信号的近似熵、样本熵、模糊熵作为信号的非线性特征[10]。近似熵(approximate entropy,ApEn)是Pincus在20年代末提取的一种非线性指标,可以对离散时间序列进行估计,计量信号的复杂性及不规则性质。在近似熵的基础上Richman和Moorman提出了一种时间序列复杂性测量方法——样本熵(sample entropy,SampEn),与近似熵相比,样本熵在计算过程中对数据长度的敏感性降低,扩大了非线性检测的适用范围,而且计算过程略去了自匹配和自适应模板算法,消除了了计算过程带来的误差。本文使用模糊熵提取脑电信号的非线性特征,模糊熵(fuzzy entropy,FuzzyEn)是Chen等针对样本熵和近似熵提取过程使用二值函数进行相似性度量导致熵值不连续而提出的一种改进算法[11]。模糊熵在计算向量的相似度时用模糊隶属度函数取代Heaviside函数,克服了二值函数方法所导致的缺乏连续性问题。该算法不仅继承了样本熵算法的优点,而且对时间序列的长度的依赖性更小,对含噪信号的鲁棒性更加优良。模糊熵算法的具体步骤如下:
(1)设N点采样序列为
{u(i):i=1~N}
(20)
(2)对上述时间序列按序号连续顺序进行相空间重构,组成m维和m+1维的矢量即
(21)
(22)
其中,i=1,2,…N-m,其中um(i)和um+1(i)分别为m维和m+1维矢量的均值。
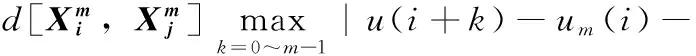
(23)
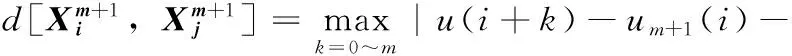
(24)
其中,i,j=1~N-m,i≠j。
(25)
(26)
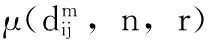
(5)定义函数
(27)
(28)
(6)定义模糊熵为
(29)
当序列长度为有限值时,可以得出模糊熵的估计值为
F(m,n,r,N)=lnΦm(n,r)-lnΦm+1(n,r)
(30)
上述函数中,m是相空间重构的维数,r是相似容限度,相似容限r选择不当会对模糊熵的估计造成影响,r的取值范围一般为0.1~0.25倍采样序列标准差,本文为了获取更大足够的序列信息,m和n的取值均为2,r为标准差的1/5。如图5所示是想象左右手运动C3、C4通道的平均模糊熵归一化值。
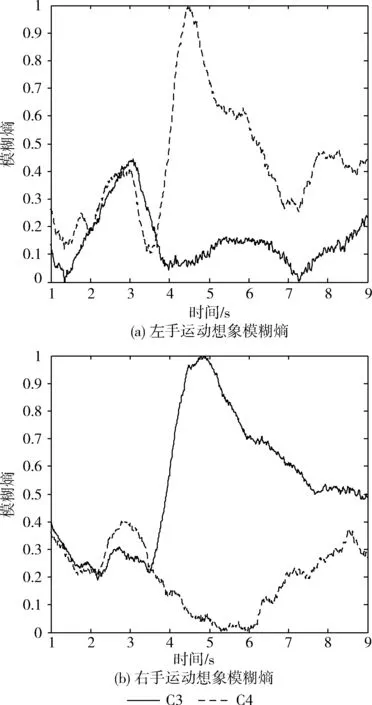
图5 想象左右手运动EEG平均模糊熵值
提取二维特征向量{FuzzyC3,FuzzyC4},表1为分别使用近似熵、样本熵、模糊熵的分类结果。

表1 不同非线性特征提取方式下的分类准确率/%
从上表可知,相对于近似熵和样本熵,模糊熵更适合用于衡量信号的复杂性,提取的非线性特征的分类正确率也更高。从理论上和实践上证明了模糊熵优于近似熵和样本熵。
2 实验结果
为验证本文所述方法的有效性,对BCI competition 2003的左右手运动想象脑电数据进行了特征提取与模式分类。将对上述CSP算法提取的二维特征向量、AR模型提取的12维特征向量和模糊熵算法提取的2维特征向量组成最终的16维特征向量{fp,C3AR1,…,C3AR6,C4AR1,…,C4AR6,FuzzyC3,FuzzyC4},形成脑电信号的多特征值提取。对提取的特征向量采用线性分类器(LDA)进行分类。线性分类器执行速度快,推广能力强,是脑机接口模式识别中最常用分类算法,在对实时性要求极高的在线系统中应用尤其广泛。LDA算法即将一个d维的样本投影到一条直线上,使得在这条直线上的样本投影能最大尺度的被分开,降低了原始信号的维度。LDA分类器的核心就是找到这一最佳投影线,能将两类样本最好地分开。表2给出了分别使用传统HHT,传统CSP和改进HCSP的算法下得到的分类准确率。

表2 不同特征提取方法下的正确识别率/%
可见当输入信号导联数较少,单一的CSP特征提取算法的分类效果最差,无法提取到有效特征向量。使用单一的HHT算法的分类准确率有了明显提高,表明HHT算法在分析非线性非平稳信号时,在时域和频域都可以具有较高的分类正确率,可以有效提取运动想象脑电的特征模式。本文在分析了HHT和CSP算法的优缺点的基础上提出了将两者结合的特征提取算法,从表2可知本文提出的HCSP特征提取方法是有效的,可以提取更为有效的分类特征。
3 结束语
本文利用HHT与CSP混合特征提取方法,获取EEG时频空域信息,既解决了人为选取IMF分量时可能混入噪声抑或丢失有用信息的问题,同时减少了输入信号的导联数。HHT算法侧重于提取脑电信号中具有可分类信息的瞬时幅值,CSP算法能够构造适用于分类的空间滤波器,同时提取AR模型参数和模糊熵。利用BCI competition 2003中提供的数据使用本文提出的特征提取方法,获得了良好的效果。
[1]Long Jinyi,Li Yuanqi,Wang Hongtao,et al.A hybrid brain computer interface to control the direction and speed of a simulated or real wheelchair[J].Neural Systems and Rehabilitation Engineering,2012,20(5):720-729.
[2]ZHAO Limin.Research on EEG feature extraction and classi-fication based on movement imagination[D].Taiyuan:Taiyuan University of Technology,2016(in Chinese).[赵利民.基于运动想象的脑电信号特征提取与分类方法研究[D].太原:太原理工大学,2016.]
[3]Atyabi A,Shic F,Naples A.Mixture of autoregressive mode-ling orders and its implication on single trial EEG classification[J].Expert Systems with Applications,2016,65:164-180.
[4]Zhou Z,Wan B.Wavelet packet-based independent component analysis for feature extraction from motor imagery EEG of complex movements[J].Clinical Neurophysiology Official Journal of the International Federation of Clinical Neurophysiology,2012,123(9):1779-1788.
[5]ZHENG Shuhua,YAN Chen,WANG Xiangzhou.A repeated bisection CSP feature extraction algorithm of four-class motor imagery EEG[J].Transactions of Beijing Institute of Techno-logy,2016(8):844-850(in Chinese).[郑戍华,闫琛,王向周.一种重复二分CSP4类运动想象脑电信号特征提取算法[J].北京理工大学学报,2016(8):844-850.]
[6]SUN Huiwen,FU Yunfa,XIONG XIN,et al.Identification of EEG induced by motor imagery based on Hilbert-Huang transform[J].Acta Automatica Sinica,2015,41(9):1686-1692(in Chinese).[孙会文,伏云发,熊馨,等.基于HHT运动想象脑电模式识别研究[J].自动化学报,2015,41(9):1686-1692.]
[7]JI Yu.Research of P300 processing algorithm based on independent component analysis[D].Hangzhou:Zhejiang University,2013(in Chinese).[计瑜.基于独立分量分析的P300脑电信号处理算法研究[D].杭州:浙江大学,2013.]
[8]YANG Banghua,LU Wenyu,HE Meiyan,et al.Novel feature extraction method for BCI based on WPD and CSP[J].Chinese Journal of Scientific Instrument,2012,33(11):2560-2565(in Chinese).[杨帮华,陆文宇,何美燕,等.脑机接口中基于WPD和CSP的特征提取[J].仪器仪表学报,2012,33(11):2560-2565.]
[9]Park C,Looney D,Rehman NU,et al.Classification of motor imagery BCI using multivariate empirical mode decomposition[J].IEEE Transactions on Neural Systems & Rehabilitation Engineering,2013,21(1):10-22.
[10]LI Conggai.The comparation and application of entropy in the detection of epilepsy[D].Taiyuan:Taiyuan University of Technology,2015(in Chinese).[李聪改.熵在癫痫信号检测中的对比研究与应用[D].太原:太原理工大学,2015.]
[11]TIAN Jing,LUO Zhizeng.Motor imagery EEG feature extraction based on fuzzy entropy[J].Journal of Huazhong University of Science and Technology(Nature Science Edition),2013,41(s1):92-94(in Chinese).[田京,罗志增.基于模糊熵的运动想像脑电信号特征提取[J].华中科技大学学报(自然科学版),2013,41(s1):92-94.]
[12]LI Lijun.Feature extraction and classification of imaginary movements in EEG[D].Guangzhou:South China University of Technology,2012(in Chinese).[李丽君.基于运动想象的脑电信号特征提取及分类算法研究[D].广州:华南理工大学,2012.]
[13]Bajaj V,Pachori RB.Classification of seizure and non-seizure EEG signals using empirical mode decomposition[J].IEEE Transactions on Information Technology in Biomedicine,2012,16(6):1135-1142.
[14]Song X,Yoon SC,Perera V.Adaptive common spatial pattern for single-trial EEG classification in multisubject BCI[C]//International IEEE/EMBS Conference on Neural Engineering.IEEE,2013:411-414.
[15]LIN Haibo,GONG Lu,ZHANG Yi,et al.Feature extraction of EEG signal based on improved HHT and sample entropy[J].Computer Engineering and Design,2015,36(6):1608-1613(in Chinese).[林海波,龚璐,张毅,等.基于改进HHT和样本熵的脑电信号特征提取[J].计算机工程与设计,2015,36(6):1608-1613.]
