代价可变的S-census变换算法

陈苏婷，吴月路，张艳艳

(1.南京信息工程大学 江苏省气象探测与信息处理重点实验室，江苏 南京 210044；2.南京信息工程大学 江苏省大气环境与装备技术协同创新中心，江苏 南京 210044)

0 引 言

立体匹配算法主要有局部的和全局的两大类匹配算法[1]。全局算法通过能量函数最小化获得匹配结果，精度较高，效率较低。局部算法利用窗口内的邻域信息来进行单像素的匹配，速度快，容易实现，但局部算法存在支持窗口的大小和合适的匹配代价选取等问题[2]。局部匹配算法对于理想图像能够获得较高精度的匹配结果，但对幅度失真非常敏感，难以用于真实场景图像的匹配。而基于census变换的匹配算法，在幅度失真方面具有较强的鲁棒性，适用于真实场景图像的立体匹配，但精度不高[3]。

针对上述基于census变换匹配算法的匹配精度不高等问题[4]，本文另辟蹊径，从改进代价计算角度以及减弱窗口变换过分依赖中心像素灰度的角度，提出一种基于可变权重代价计算与S-census变换(variable support-weight S-census transform，VSC)立体匹配算法。解决了单一匹配代价[5]计算带来的匹配误差高、窗口变换过度依赖中心像素灰度等问题。同时，算法在深度不连续区域也能够得到比较精准的视差图。最后，实验结果验证了算法的有效性和实用性。

1 VSC算法的提出

局部匹配算法的核心就是采用待匹配像素周围的信息进行计算[6]。主要有区域匹配、特征匹配、相位匹配3大类。局部区域的非参数census变换立体匹配算法的实现主要步骤[7]是：首先对输入的左右图像进行census变换，对变换后的左右图像计算汉明距；其次进行非局部代价聚合；最后采用WTA(winner-take-all)策略[8]进行视差计算，得到最终的视差图。

非参数census变换匹配算法，虽然能改善图像受噪声干扰时的匹配效果，主要有以下两方面的不足：①未利用邻域像素的灰度信息，变换结果未考虑邻域像素间的比重关系。②匹配代价计算单一，对异常点辨识度不够，易造成误匹配。因此，本文针对局部的非参数census变换的立体匹配算法的以上两点缺陷，提出了VSC立体匹配算法，算法流程如图1所示。

图1 VSC算法流程

如图1所示，提出可变代价的S-census变换(variable cost S-census transform，VSC)算法。基本原理如下：首先在对周围邻域像素信息获取方面，利用S-census变换替代原census变换，邻域像素信息得到充分利用，提高算法匹配精度；其次，可变权重代价计算方法，能够辨识异常点，减少误匹配。最后，在基于非局部代价聚合获取初始视差图后，利用均值偏移的视差提精方法，处理不可信区域，进一步提高视差精度，获得最终视差图。

在选取匹配窗口问题上，本文利用ORB[9]特征提取算法并配对，以匹配点为中心建立3×3大小的匹配窗口，ORB算法参考文献[9]所述。在获取匹配窗口后，本文算法分3个部分实现：S-census变换对窗口像素处理，采用可变权重匹配代价方法计算代价、获得单像素视差，代价聚合法获得初始视差图，对初始视差图进一步视差优化获得最终视差图。具体实现方案如下文。

2 S-census变换方法的提出

2.1 传统Census变换

Census变换是局部的非参数变换，过程简单。对图像I中的像素p进行census变换，首先，选取窗口W(p)，p为中心。把窗口中各像素Q与p比较灰度值。假如Q处大于p处的，那么Q处变换结果β(Q,p)为0，否则为如式(1)所示

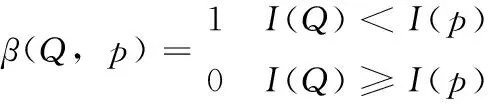
(1)

p点的census变换可以表示为

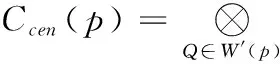
(2)

式中：⊗是连接相继两个比较结果，W′(p)是W(p)中不包含p的点集。根据以上所述方法可得二进制串。

2.2 S-census变换方法

本文提出一种基于星型邻域的S-census变换方法来解决传统census变换的不足，S-census变换方法能够消除中心灰度变化的影响、有效地处理诸如角点等特征。

S-census变换算法步骤如下：

(1)以(u,v)为中心的窗口，划分窗口内以过(u,v)为点的各条线段。线段划分方式如图2所示。

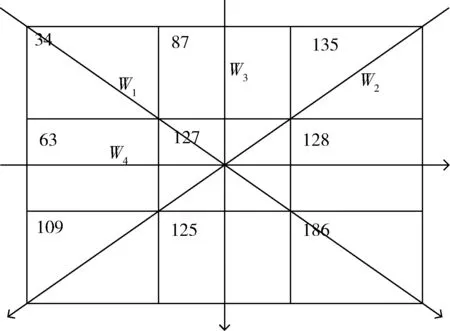
图2 星型邻域线段划分

(2)计算各条线段上的灰度均匀度w

(3)

(3)取最小分布均匀度w，w对应的区域灰度均值替换中心点(u,v)的灰度值。

(4)如2.1节所示方法进行census变换。

这里，过点(u,v)的所有线段组合成star型，这也是本文所提的S-census(star-census)变换的由来。

线段W1,W2,W3,W4组成星状，这也是本文所提星型邻域的由来。根据式(2)可以得到如图3所示各星型邻域的灰度分布均匀度分别为W1=11 705，W2=355，W3=1016，W4=2774。因为W2最小，所以取其对应区域的灰度均值124作为中心点(u,v)灰度值，替换原灰度值127。

传统的census变换如图3所示，得到的二进制码串为110100110。当窗口中心像素灰度在I′∈(110,125]范围变化时，采用如图3所示的传统census变换得到的二进制串由110100110变为110100100。

图3 传统Census变换

如图4所示为S-census变换图，得到的二进制码串为110100100。当窗口中心像素的灰度值变换在I′∈(110,125]范围变化时，经S-census变换后，二进制串仍然是110100100，未有任何改变。由此可见，在抗干扰能力方面得到了有效地增强。缩小census变换过度依赖中心点亮度的情形，匹配代价计算精确度方面有了很好的提高。

图4 S-census变换

3 可变权重匹配代价方法的提出

3.1 传统基于汉明距的匹配代价计算

建立在S-census变换的基础上，为了实现立体匹配，需进行匹配代价计算与代价累积。而传统基于census变换在匹配代价计算与代价累积上，对census变换后，对应点间进行汉明距计算[10]，统计对应像素点的距离和来确定最佳匹配点。

代价计算公式如下

C(u,v,f)=Hammin(w1(u,v),w2(u-f,v))

(4)

式中：w1(u,v)代表左窗口S-census变换结果，w2(u-f,v)表示右边窗口S-census变换结果，f表示窗口对应点的视差距离。

代价累积公式如下

(5)

式中：m和n分别代表匹配窗口的宽度和高度，在设定视差f范围内，CSum最小时对应的标号即为该点的视差。

3.2 可变权重匹配代价计算

使用传统的代价计算方法，其作为相似性测度方法，在深度间断跳跃等区域误匹配率高。原因是这种代价计算相似性测度过于单一，对异常值的辨识度不够。因此，本文提出了基于汉明距的可变权重匹配代价计算方法。

基于权重可变汉明距的代价计算步骤如下：

(1)计算窗口大小h,h=m×n。

其中m和n分别代表匹配窗口的宽度和高度。h即表示经窗口变换后码的长度。

(2)对变换的码值依次赋予权重，权重因子δk

(6)

式中：k表示对变换码编号，从左到右依次为1到h。

(3)可变权重代价计算。

代价计算公式如下

(7)

式中：w1k(u,v)表示左窗口对应编号k的码，w2k(u-f,v)表示右窗口对应编号k的码。

4 代价聚合与视差优化

基于可变权重汉明距代价计算获取单像素视差的基础上，需进行代价聚合以获取视差图，Yang提出了一种非局部代价聚合方法，此种方法复杂度比较低，能够自适应的聚合匹配代价。本文使用这种代价聚合方法。具体实现方法如参考文献[9]所述。

为进一步提高视差的区分性，采用一种均值偏移的视差提精方法进行视差优化，具体实现步骤如下：

(1)对于不可信的初始视差，用左右一致性的方法来进行检测。经过左右一致性方法[11]检测后，参考图像视差估计主要分为高置信度集Dhc和低置信度集Dlc。

(2)视差图采用均值偏移方法分割成子区域，每个子区域记为Si。建立可信视差估计统计直方图Si，统计不同视差出现次数。

(8)

5 实验结果与分析

为了验证VSC算法的有效性，在MATLAB和VS2010+opencv软件平台上进行了实验验证。采用Middlebury网站的4幅标准图Cones图、Teddy图、Tsukuba图、Venus图等进行了测试分析。实验分别从3个方面对VSC算法进行验证。①改进前后变换匹配率的比较验证；②代价区分度验证；③算法可行性验证。详细内容如下几节所述。

5.1 S-census变换与census变换匹配率的比较

实验通过对两种变换支持窗口大小的改变，来比较不同窗口下的匹配率。没有进行代价聚合，这样能够验证两种变换对匹配的影响。支持窗口大小从3*3到15*15。选取标准测试图像Cones图、Teddy图、Tsukuba图、Venus图。结果如图5所示。

从实验结果图5可以看出，改进后的S-census变换匹配率明显好于census变换匹配率。平均4个实验结果图，匹配率大概提高了15%左右。说明S-census变换能够有效地削弱变换过度依赖中心像素灰度的情况，验证了S-census变换的有效性。

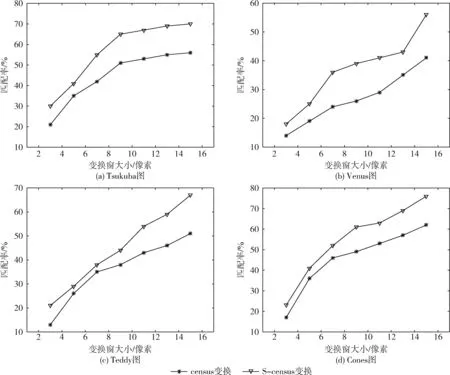
图5 S-census变换与census变换匹配率对比

5.2 代价区分度验证

传统census变换的相似性测量标准是计算Hamming距，为验证本文所提可变权重代价计算的有效性，实验采用抽样匹配点来进行验证两种代价计算区分度，即算法正确匹配点率，即(1-误匹配点率)×100%。误点率计算公式如下

(9)

δthresh为视差容差，N为像素总数，dc(x,y)为测试视差，dt(x,y)为真实视差。如图6(a)所示对Teddy测试图选取抽样点，以保证其它条件一致的情况下，实验选取不同的视差值来验证改进前后代价计算的区分度。实验结果如图6(b)所示。

由图6(b)，当选取视差值递增时，改进后代价计算方法如三角形线条显示，算法的区分度明显高于星形线条所表示的传统代价计算方法的区分度，在视差选取值为6时，前后代价计算区分度相差不大，这是因为此处实验预设真实视差值为6，不影响整体算法区分度的验证。实验结果表明改进后的代价计算方法区分度更高。

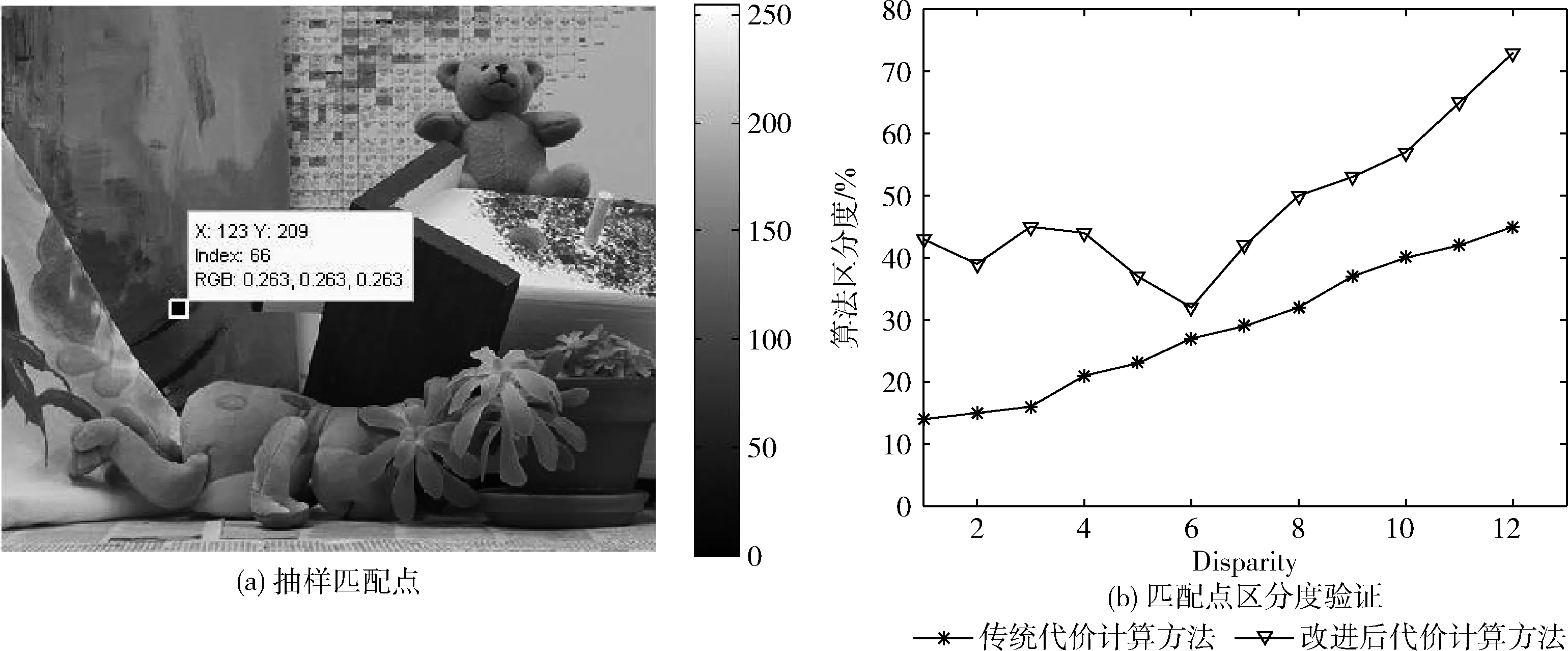
图6 匹配点区分度对比

5.3 算法可行性验证

最后验证算法可行性，对比实验分析了本文算法与其它几种匹配算法的误匹配率，并对Middlebury平台的4幅标准图进行实验，将实验视差图与标准视差图对比，充分说明本文算法的可行性。

表1是不同算法误匹配百分比统计实验结果，其中nonocc、disc、all表示非遮挡区域、视差不连续区域、所有区域。误匹配像素百分比E为

(10)

式中：dc(x,y)是点(x,y)在改进算法得到视差图中的视差值，dt(x,y)是真实视差图中的视差值，M为图像大小，误差限δd=1，即当匹配结果与真实视差图相差1 pixel以上时，认为该点是误匹配点。几种不同算法实验结果见表1。

表1 不同算法误匹配百分比/%

由表1可知，CostFilter均误匹配比率是5.54%，Assw-Grad均误匹配比率是6.1%，AdpDP均误匹配率是9.82%。VariableCross均误匹配率是7.60%，本文VSC算法均误匹配率是5.83%。从以上实验数据整体上来看，本文算法优于Assw-Grad、AdpDP、VariableCross等算法。其中CostFilter是当前最好的局部匹配算法。

验证算法的有效性，实验对Middlebury网站的4幅标准图像进行了测试，标准测试图像从左到右依次是Cones图、Teddy图、Tsukuba图、Venus图。分辨率为450 pixel×375 pixel、450 pixel×375 pixel、384 pixel×288 pixel、434 pixel×383 pixel。实验时，4组图像的视差搜索范围为0-60 pixel、0-60 pixel、0-16 pixel、0-20 pixel。实验结果如图7所示。

图7 本文实验结果与Ground Truth对比

如图7所示，VSC算法结果与真实视差图的比较，本文VSC算法得到的视差图整体比较光滑，在视差不连续区域和平坦区域可以取得较好的效果。

实验总结：实验分别从3个方面对VSC算法进行验证：①改进前后变换匹配率的比较验证；②算法区分度验证；③算法可行性验证。综上3个指标实验验证，充分说明了本文所提VSC算法具有可行性。

6 结束语

本文提出的VSC算法，克服了传统census变换算法过度依赖中心像素灰度值的缺陷，解决了现有算法难以从图像中获取高精度视差的问题。在立体匹配时，通过加权区域海明距离均值和标准差信息来提高匹配的精度。采用非局部代价聚合方式，提高视差的可区分性，对于获得的初始视差，进一步采用基于均值偏移的视差提精方法，有效的处理了不可信视差区域，提高了视差精度。提出的VSC算法在匹配点权值区分度方面得到显著提高。S-census变换与census变换相比，匹配率提高了约15%。改进后的代价计算方法在视差匹配时区分度更高。与当前优秀的局部匹配算法CostFilter匹配精度相当，在深度不连续区域也能够得到比较精准的视差图。能够实现高精度的立体匹配。将VSC算法应用于机器人自主导航地图构建中将是以后的主要研究方向与研究重点。

[1]ZHU Shiping,YAN Lina.Stereo matching algorithm based on improved Census transform and dynamic programming[J].Acta Optical Sinica,2016,36(4):208-216(in Chinese).[祝世平,闫利那.基于改进Census变换和动态规划的立体匹配算法[J].光学学报,2016,36(4):208-216.]

[2]ZHU Shiping,LI Zheng.Based on the improved gradient and stereo matching algorithm of adaptive window[J].Acta Optical Sinica,2015,35(1):115-123(in Chinese).[祝世平,李政.基于改进梯度和自适应窗口的立体匹配算法[J].光学学报,2015,35(1):115-123.]

[3]MEN Yubo,MA Ning,ZHANG Guoyin,et al.Nonparametric transform and improve dynamic programming stereo matching algorithm[J].Journal of Harbin Institute of Technology,2015,47(3):60-65(in Chinese).[门宇博,马宁,张国印,等.非参数变换和改进动态规划的立体匹配算法[J].哈尔滨工业大学学报,2015,47(3):60-65.]

[4]De-Maeztu L,Villanueva A,Cabeza R.Stereo matching using gradient similarity and locally adaptive support-weight[J].Pattern Recognition Letters,2011,32(13):1643-1651.

[5]Zhan Y,Gu Y,Huang K,et al.Accurate image-guided ste-reo matching with efficient matching cost and disparity refinement[J].IEEE Transactions on Circuits & Systems for Video Technology,2016,26(9):1632-1645.

[6]Fan X,Wang X,Xiao Y.A shape-based stereo matching algorithm for binocular vision[C]//International Conference on Security,2014:70-74.

[7]Xu L,Au OC,Sun W,et al.Stereo matching with optimal local adaptive radiometric compensation[J].IEEE Signal Processing Letters,2015,22(2):131-135.

[8]Chang X,Zhou Z,Wang L,et al.Real-time accurate stereo matching using modified two-pass aggregation and winner-take-all guided dynamic programming[C]//International Confe-rence on 3d Imaging,2011:73-79.

[9]Rublee E,Rabaud V,Konolige K,et al.ORB:An efficient alternative to SIFT or SURF[C]//IEEE International Confe-rence on Computer Vision,2012:2564-2571.

[10]Zhang K,Fang Y,Min D,et al.Cross-scale cost aggregation for stereo matching[C]//IEEE Conference on Computer Vision & Pattern Recognition,2014:1590-1597.

[11]Lee Z,Juang J,Nguyen T.Local disparity estimation with three-mode cross census and advanced support weight[J].IEEE Tran-sactions on Multimedia,2013,15(8):1855-1864.

[12]Salehian B,Raie A,Fotouhi A,et al.Efficient interscanline consistency enforcing method for dynamic programming-based dense stereo matching algorithms[J].Journal of Electronic Imaging,2013,22(4):043028.