基于扩散码的图像加密算法
2018-03-16张大兴刘志发陈辉映
张大兴,刘志发,武 健,陈辉映
(杭州电子科技大学 图形图像研究所,浙江 杭州 310018)
0 引 言
计算机存储数字图像数据有其特点:①信息量大;②数据相关性高;③允许一定程度的修改。传统的加密方式一般是针对二进制流和文本信息设计的,并没有考虑图像数据的特殊性,无法打破像素间的高相关性,同时,由于图像存储数据量大,如何提高图像加密的效率也是一大问题[1]。当前对于图像加密主要有以下几个研究方向,基于图像像素置乱的图像加密算法、基于混沌的图像加密算法、基于变换域的加密算法、传统加密算法的改进算法,总体而言,算法各有优缺点[2,3]。近年来随着GPU通用计算技术的软硬件迅速发展,不少学者结合图像自身特点在图像应用领域加以应用并取得一定的成果,使得图像处理速度大大增加[4-6]。文献[7]中提出了一种扩散码结合布尔构造分组密码的思想,与现有的体制相比(如FEAL-N,DES等)具有操作指令单纯、扩散速度快、适合并行等特点。本文结合扩散码的思想,将其用于数字图像加密中,实验仿真数据分析结果表明,算法能够快速完成加密并具有较高的安全性,同时将图像加密算法结合CUDA技术给出一种实现方案,结果表明,GPU平台下实现算法能够大幅度提升算法效率。
1 扩散码基础单元
首先引入单比特扩散码概念并介绍扩散码基础单元。
1.1 扩散过程
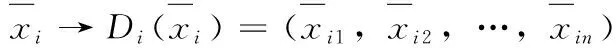
得到矩阵[D]
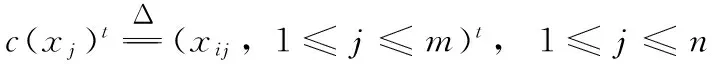
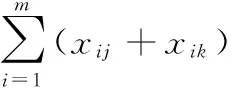
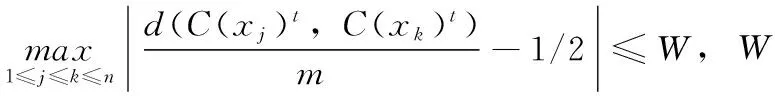
(1)当m为偶数时,使用任意阶Hadamard矩阵的列可以构造W=0为最小偏移值;
(2)当m为奇数时,通过Legendre序列等可以构造W=1/2m最小偏移值。
1.2 混合过程
上述过程通过扩散码[D]实现输入xi映射成扩散码矩阵,混合过程则通过选择安全可靠的布尔函数B对扩散码矩阵行向量进行逻辑运算来完成。即Di(xi), 1≤i≤m为输入量,按布尔函数B进行逻辑运算
Y=B(D(x))=(yi,1≤i≤n)
其中,yi=f(xij,1≤i≤m)。
可以看出每一个输入变量能够影响到任意一位输出变量,经过一次扩散混合运算可以完成所有数据的混合。文献[8]中指出合适的布尔函数能够保证扩散、混合的效果,而布尔函数的设计应满足3个准则:①平衡性;②非线性度;③严格雪崩准则(SAC),由于求解布尔代数方程组是1个NP完全性的问题[9],合理设计的布尔函数能够保证计算上的安全性。文献[10]通过对扩散码思想分析,给出了一种满足上述准则的布尔函数
B=x1x3+x2x4+x3x5+x4x6+x5x7+x6x8+
x7x1+x8x2+x3x6x7+x1x2x6+x2x4x7+
x2x5x7+x1x5x6+x1x2x3+x6x7x8
公式中运算均指逻辑运算。式中x1~x8只能表示分组大小为8 bit的数据长度,若分组更大则可以通过公式的多次循环来构建对应映射关系。本文算法将使用该布尔函数进行混合运算。
1.3 基础结构单元
通过一次扩散、混合能够完成分组内每个比特扩散到全比特,我们定义这个过程为基本单元SU,图1为整个SU流程。对于SU整个过程只有两类操作:扩散过程实现信元扩散映射,只需对存储器访问操作,而混合过程由各码字间位运算完成。这两类基本操作无论对硬件还是软件都是基本操作,GPU是针对向量进行优化的数据流处理机,因此GPU平台实现该过程拥有独特的优势,为验证扩散码算法GPU平台下的高效性,文中将在GPU平台上进行算法实现。
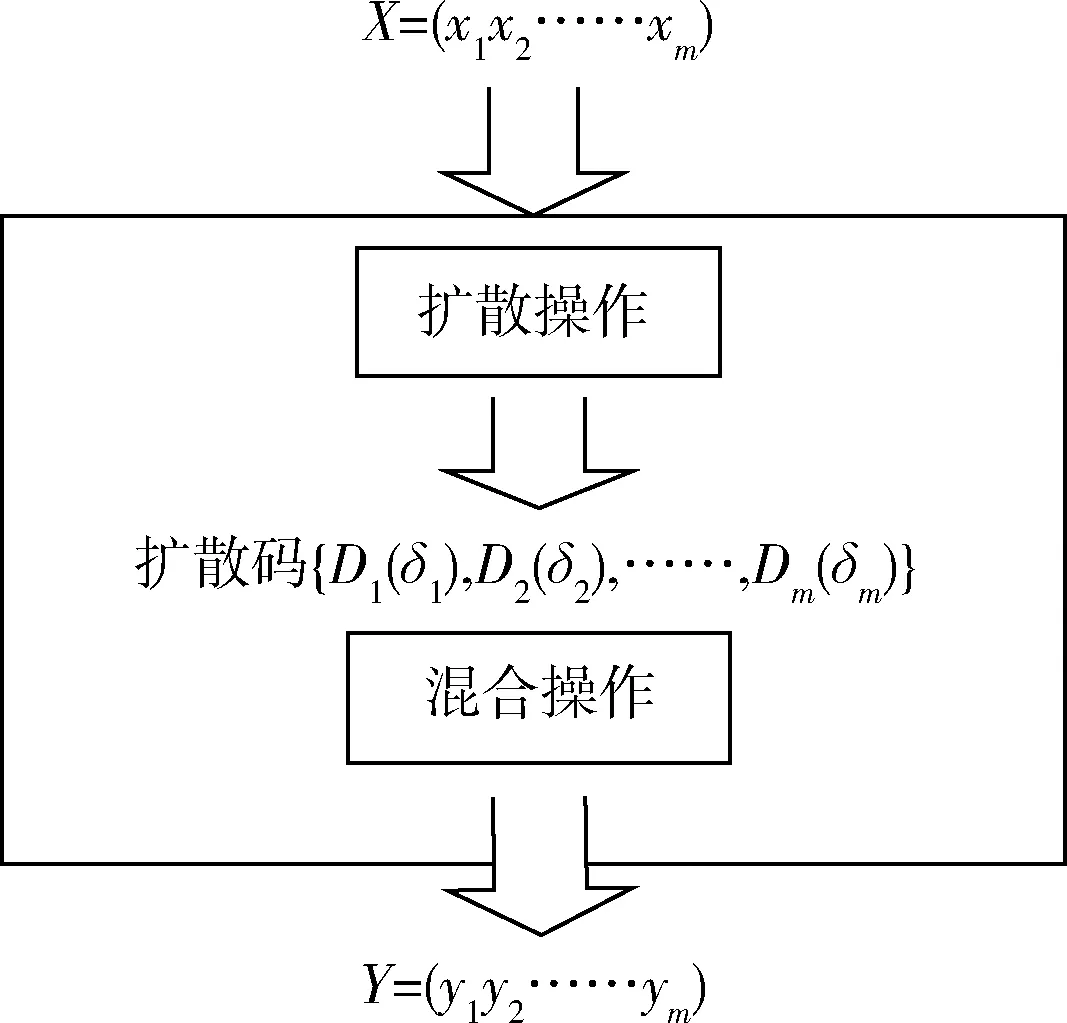
图1 扩散码基础单元
1.4 Feistel密码结构
在密码学中,Feistel密码结构是用于分组密码中一种特殊的对称结构。由于是对称的密码结构,因此对信息的加密解密过程几乎完全一样,实施过程中,对编码和信息传输效率更高。Feistel密码结构代数表达式如下
Ri=Li+1
Li=Ri+1⊕F(Li+1,Ki)
在每一轮加密过程中输入长度为2W的明文和对应秘钥序列(k1,k2…kn)。将明文部分为左右两部分LxRx进行F计算,经过多轮迭代过程明文的统计特征将被掩盖,其中函数F是加解密过程中的唯一非线性部分,函数F复杂度决定了加密算法的安全性[11]。
2 图像加密中应用
2.1 CPU平台算法实现分析
通过基本单元代替Feistel中的F函数实现图像加密过程,并根据算法流程(如图2所示)依次介绍扩散码算法应用于图像加密的主要过程。
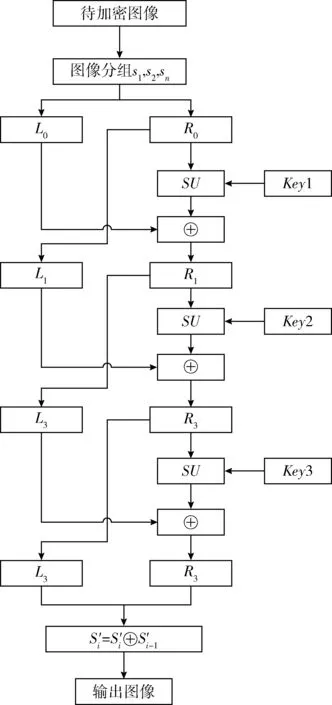
图2 图像加密算法流程
对基础单元的分析可以发现,分组大小直接影响算法速度性能,因为它决定读取存储器的次数与逻辑运算次数,SU理论上对于任意大小的分组都可以很好地完成整个分组的扩散,但考虑到实际加密应用中(如文本、图像的加密)相邻数据具有相关性,此参数也不能太小,因此结合速度与实际应用本文选择以32*8 bit作为一个分组进行算法描述。
2.1.1 图像预处理
输入图像P是一个M*N的灰度图(对于真彩色图像可以分别对RGB通道进行处理),对图像进行分组,n=((M*N)/64)组。
2.1.2 算法实现

2.1.3 解密过程
由于Feistel是一种特殊的对称结构,加解密过程基本一致,解密中只需要对图像从最后一个分组进行解密,秘钥和轮数与加密时相反即可。
2.2 GPU平台算法实现分析
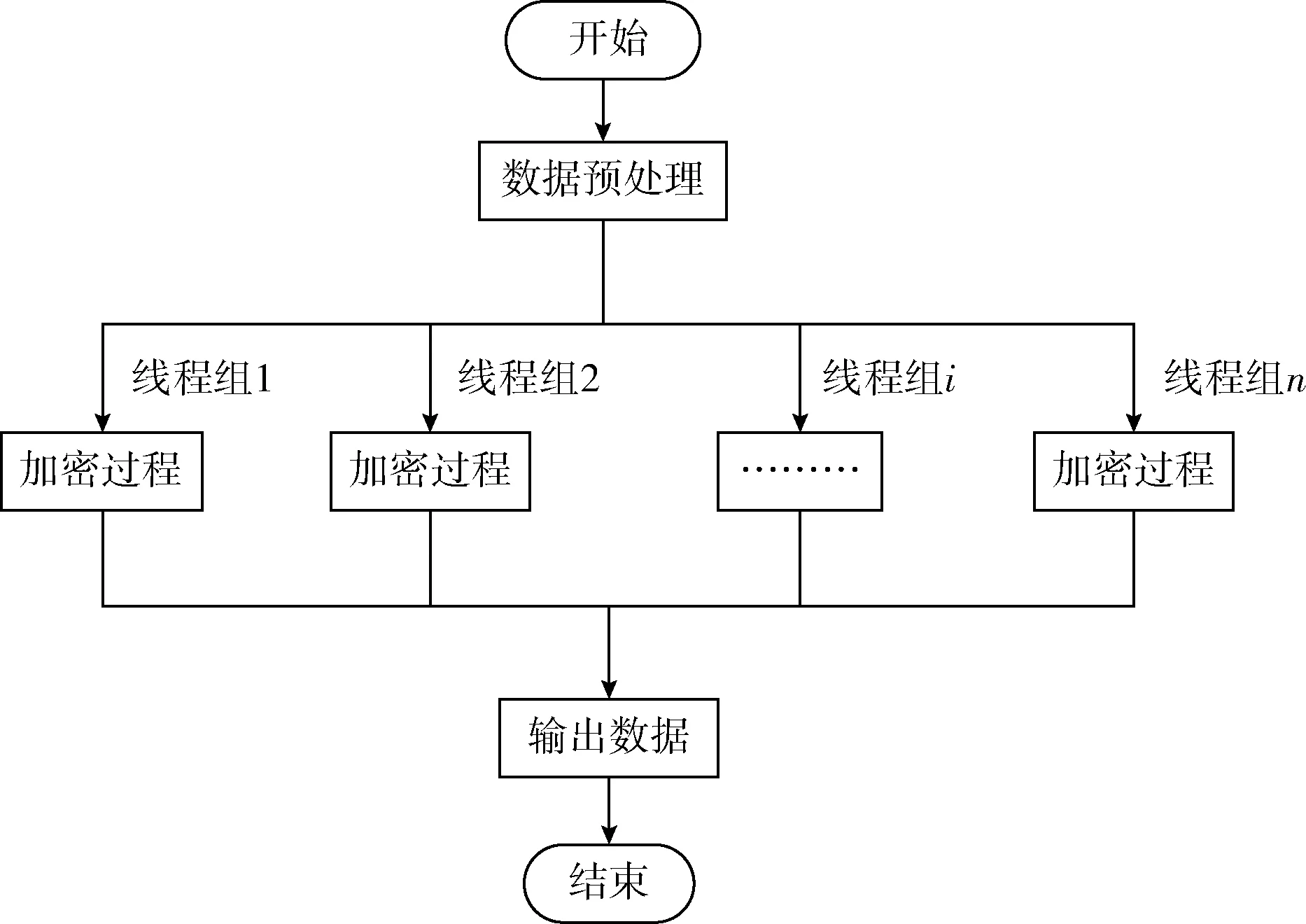
图3 图像加密并行算法流程
3 实验结果和分析
为验证算法的安全性和实用性,本文进行了仿真实验,实验软硬件配置为:①CPU双核Inteli5-2400,主存3.24 G;②GPU采用NVIDIA GTX760,显存2 G。实验程序分别在VS2010和CUDA7.5环境编译运行。实验中采用了标准图像Cameraman等灰度图片进行测试,图片大小512×512。加密、解密过程中使用到的秘钥我们采用最简单的key=12345678901234567890123456789012,共32*8位。
在图4(a)为原图像,图4(b)是加密后的图像,从视觉效果上,加密后的图像是完全混乱的一个噪声图像,无法通过图像的纹理特征来推测原图,图4(c)是使用正常秘钥解密后的图像,与原图完全一样,图4(d)中使用错误秘钥key=02345678901234567890123456789012,进行解密的效果,发现即使只有一个bit位的变化,解密后的图像也完全是混乱的。

图4 加密与解密效果
3.1 算法速度性能
算法在GPU平台进行了初步速度性能探究,实验分别在GPU与CPU下进行实现,测量时间均为绝对时间,如表1,图5所示。
表1和图5表明对于SU基本模块采用GPGPU并行技术实现该过程带来了非常高的加速效果,随着数据量的增加GPU的加速效果更加明显,最终趋于250倍左右,表明本文算法中基础单元很适合GPU架构实现,由于SU是结构化基础结构,同样可用于其它过程。同时,对于SU用于图像加密中同样取得了180倍左右加速比,可以完成对图像的快速加密。
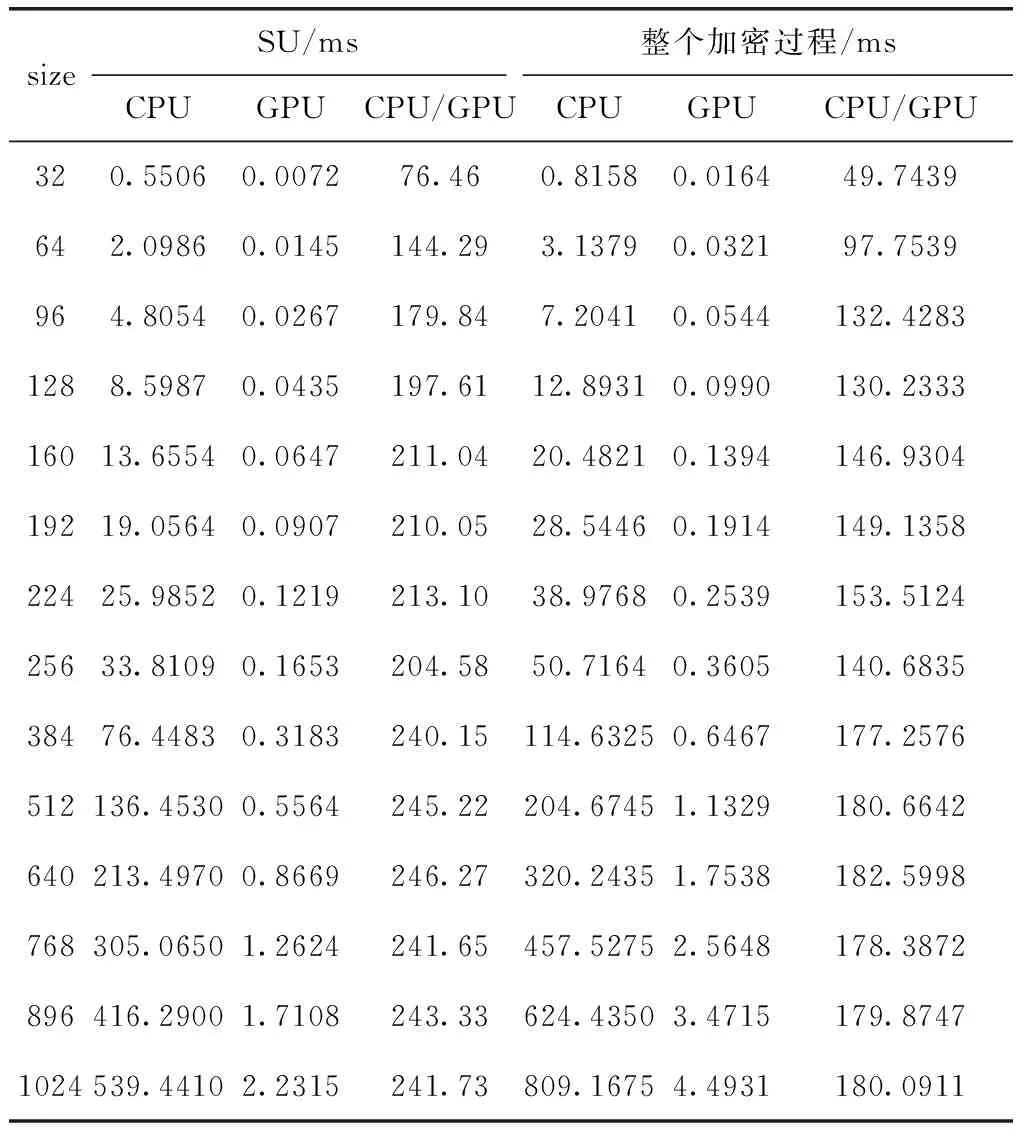
表1 CPU与GPU平台时间对比
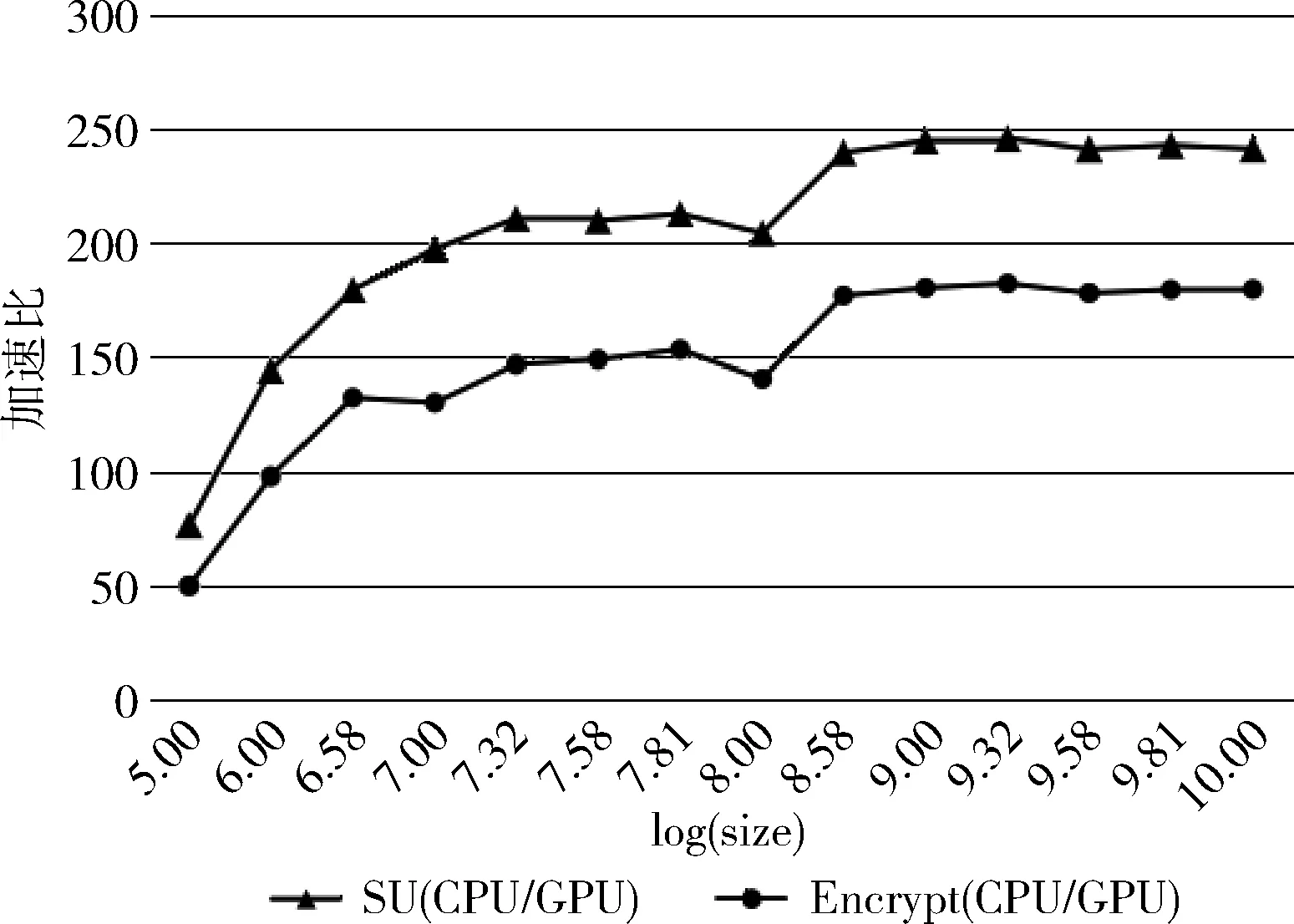
图5 算法CPU与GPU实现时间对比
3.2 秘钥空间分析
文中提出的算法秘钥与分组大小有直接相关,与DES算法中固定64分组大小相比,本文提出的算法秘钥空间大,分组也更灵活。对于文中我们采用的分组大小为32*8 bit,则秘钥空间为N*2256,可以看出算法中的秘钥空间足够大,若分组变大,秘钥空间随之变大,能够有效抵抗穷举攻击,保证图像加密过程的安全性。
3.3 直方图分析
图像的直方图是用于反映图像中像素点的分布情况,一副完全混乱的图像直方图应符合均匀分布。图6展示了加密前和加密后的图像直方图。
图6表明,经过扩散码加密算法加密后,直方图从原来的有规律分布变成完全均匀分布,说明图像的灰度级发生了很大改变,算法能够有效的抵抗直方图攻击。
3.4 相邻相关性分析
相关性是定量衡量两个变量之间关系的参数,好的图像加密算法应能够保证相邻像素间的低相关性。为了衡量加密图像后的像素相关系数,我们分别从明文图像和密文图像中随机选取3000个像素点进行垂直方向、水平方向和对角线方向的相关度计算,计算公式如下
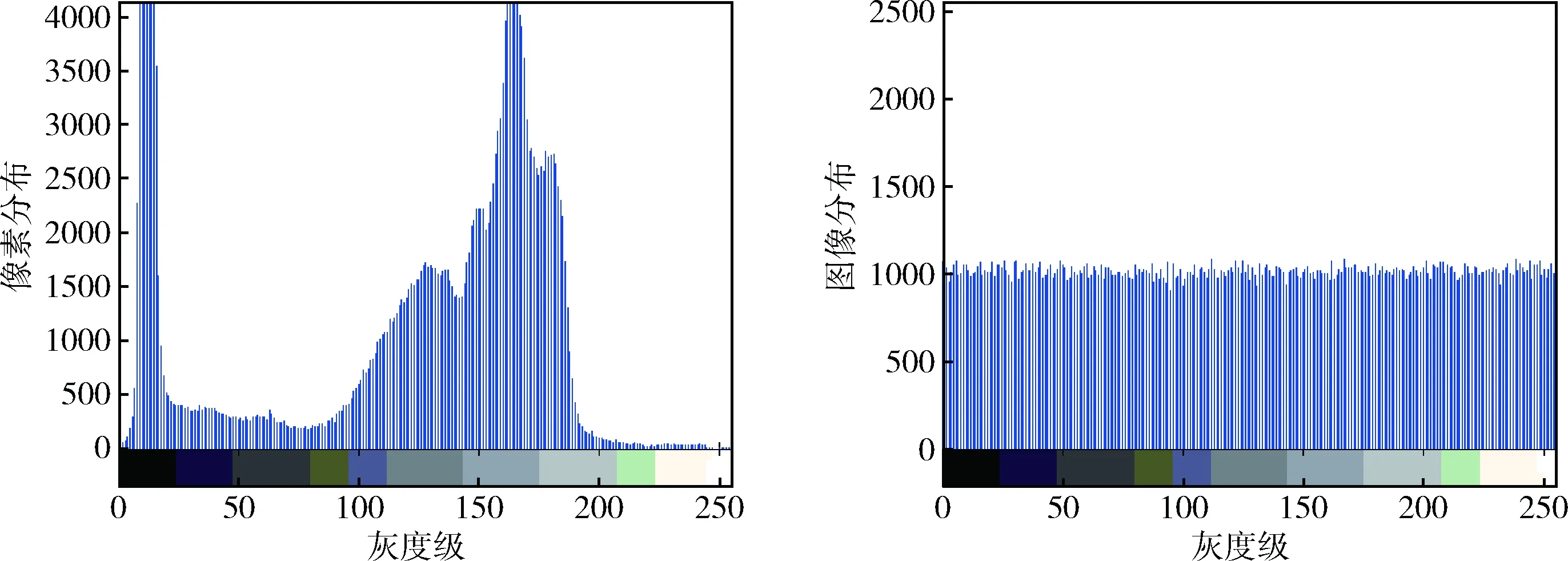
图6 Carmeraman原图(左)与加密后图(右)直方图
其中,E(x)和D(x)分别表示x的均值和方差,N为总的像素点数。
图7、表2表明,原图中各个方向相邻像素点的相关性接近1,分布存在Y=X线性关系,而加密后的图像这种关系完全消失,因此算法能够有效地破坏相邻像素间的相关性。
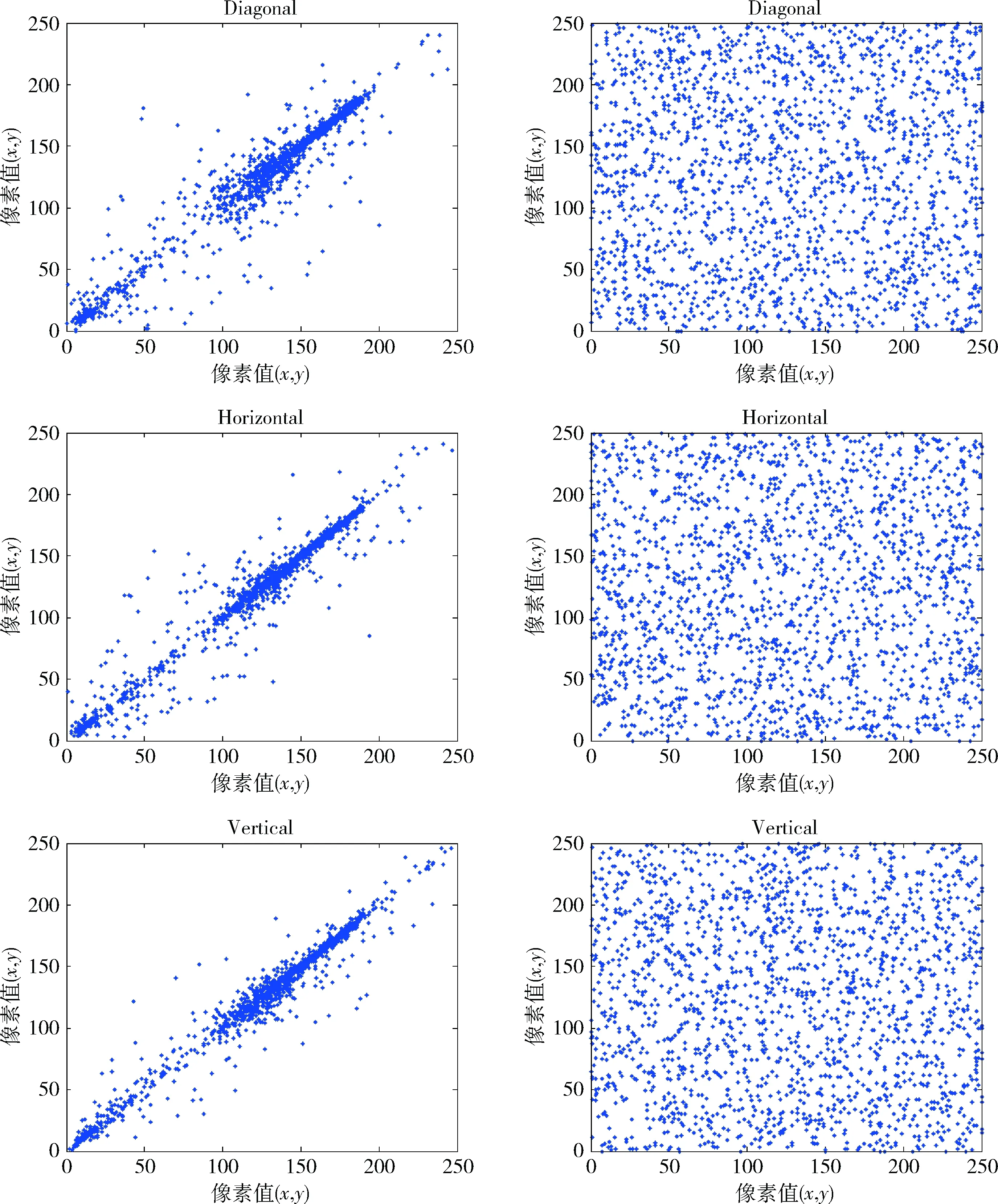
图7 加密前后像素相邻相关性对比
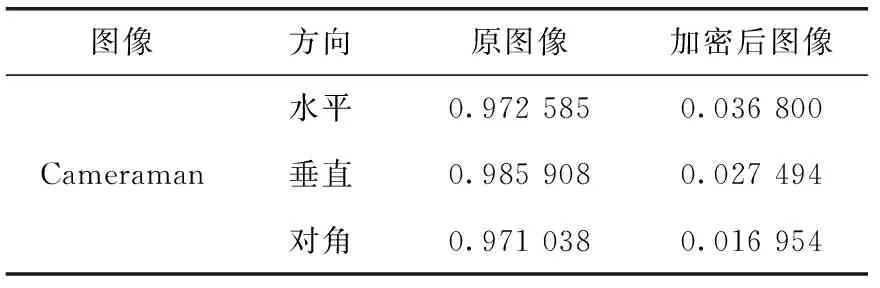
图像方向原图像加密后图像Cameraman水平0.9725850.036800垂直0.9859080.027494对角0.9710380.016954
3.5 熵值分析
在信息论中,熵是对不确定性的测量。对于图像,信息熵越高表明图像分布越均匀,反之则图像分布是有规律的。图像熵值计算公式如下
式中:P(mi)代表状态mi在图像中出现概率,对应∑P(mi)=1。 一幅理想的加密图像,其熵值H(m)=8,此时图像是完全随机的。表3是对加密前后熵值的统计。
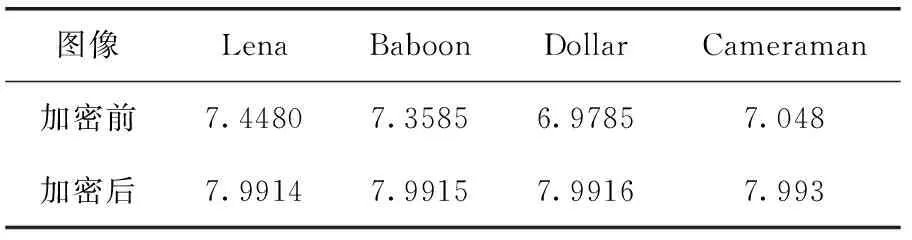
表3 原图像和加密后图像熵值对比
加密后的图像熵值非常接近8,说明扩散码加密算法可以有效抵抗熵值分析攻击。
4 结束语
扩散码作为Feistel加密结构中F函数是一种安全性好、效率高的加密方式,加密过程中只需要进行行按位逻辑和存储器访问两类基本操作,利于软硬件实现。本文将扩散码理论用于图像加密进行新的探究,实验结果表明,算法能够很好地抵抗常见的攻击手段;同时给出算法在GPU实现方案,证实利用GPU平台能够充分发挥扩散码算法的优势。本文仅仅对扩散码用于图像加密进行了实践,扩散码也可用于校验码、认证码,另外如何充分利用GPU资源高效实现算法有待研究。
[1]Abusukhon A,Talib M,Nabulsi MA.Analyzing the efficiency of text-to-image encryption algorithm[J].International Journal of Advanced Computer Science & Applications,2012,3(11):35-38.
[2]ZHANG Xiaoqiang,WANG Mengmeng,ZHU Guiliang.Research on the new development of image encryption algorithms[J].Computer Engineering & Science,2012,34(4):17-22(in Chinese).[张晓强,王蒙蒙,朱贵良.图像加密算法研究新进展[J].计算机工程与科学,2012,34(4):17-22.]
[3]LUO Xixi.Digital image processing algorithm based on GPU[J].Electronic Technology & Software Engineering,2016(19):93(in Chinese).[罗喜喜.基于GPU的数字图像处理算法[J].电子技术与软件工程,2016(19):93.]
[4]Mondal S,Maitra S.Data security-modified AES algorithm and its applications[J].Acm Sigarch Computer Architecture News,2014,42(2):1-8.
[5]Heidari H,Chalechale A,Mohammadabadi AA.Parallel implementation of color based image retrieval using CUDA on the GPU[J].International Journal of Information Technology & Computer Science,2013,6(1):33-40.
[6]Zhu L,Zhou Y,Zhang D,et al.Parallel multi-level 2D-DWT on CUDA GPUs and its application in ring artifact removal[J].Concurrency and Computation:Practice and Experience,2015,27(17):5188-5202.
[7]YE Youxin.Diffusion codes and their cryptographic utilities[J].Journal on Communications,1997,18(9):20-26(in Chinese).[叶又新.扩散码及其密码学用途[J].通信学报,1997,18(9):20-26.]
[8]ZHANG Daxing,YE Youxin.The design of Boolean function used in application of diffusion codes[J].Information Security and Communications Privacy,1997(4):46-49(in Chinese).[张大兴,叶又新.扩散码应用中布尔函数的设计[J].信息安全与通信保密,1997(4):46-49.]
[9]Joshi AB.On Boolean functions in the context of coding theory and cryptography[J].Journal of Urology,2012,193(4):e568-e569.
[10]YE Youxin,YANG Ling.The combinatorial security of Boolean functions and diffusion codes[J].Chinese Journal of Compu-ters,1999,22(4):337-342(in Chinese).[叶又新,杨玲.布尔函数与扩散码的组合安全性[J].计算机学报,1999,22(4):337-342.]
[11]Zhang X,Mao Y,Zhao Z.An efficient chaotic image encryption based on alternate circular S-boxes[J].Nonlinear Dynamics,2014,78(1):359-369.
[12]Yang Y,Xiang P,Kong J,et al.A GPGPU compiler for memory optimization and parallelism management[J].Acm Sigplan Notices,2010,45(6):86-97.
