抽水引起的土层与地面沉降规律

杨建民，隋颜阳，纪森林

(1.天津大学 建筑工程学院土木工程系，天津 300072； 2.天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072)

抽水引起的土层沉降问题是一个已经有很久研究历史的经典课题，随着国家工程建设尤其是地下空间开发兴起再次成为一个热点问题。在地下工程建设中，井点降水是常常采取的一种控制地下水位的施工措施。除了控制地下水位，工程降水时的另一关注点是降水引起的地面沉降和土层分层沉降。土体变形会影响周边环境和建筑物、构筑物，变形过大还会引发工程事故，因此预测或推算抽水导致的土层沉降成为地下工程建设的一个重要问题。

计算抽水引起的土层沉降尤其是地表面沉降，主要可分为3类方法：①分层总和法，该方面的文献不胜枚举；②数值计算方法，它可以考虑复杂的本构关系、边界条件和多种影响因素，如应用ANSYS、ABAQUS、FLAC、MODFLOW、FEFLOW等；③某些限制条件比较严格、适用范围有限的理论解析解。这些方面的方法列举如下。

分层总和法类型的文献，如曹文贵等[1](2013)考虑地基变形的非线性变化特征，引进增量分析方法、胡克定律和Duncan-Chang模型，建立了由附加体积应力和附加偏应力引起的地基压缩层变形的分析方法，并利用地基沉降分层总和法分析原理，建立了基于Duncan-Chang模型的地基沉降分析新方法。

数值计算法类型的文献，如BURBEY等[2-3](2006)在Nevada的Mesquite开展了为期62 d的大型抽水试验，试验井深500 m，应用GPS测量地面变形，应用多种数值计算模型如UCODE、MODFLOW-2000、BIOT轴对称有限元程序和颗粒流程序，对试验中监测所得地面水平位移、竖直位移进行分析。KIHM等[4](2007)应用有限元地下水化学数值计算软件COWADE123D研究了一块非饱和冲积地层的水位变化和沉降发展历史，其中土体变形采用弹性模型。SHI等[5](2008)将地下水三维渗流模型与土体一维沉降模型相耦合，研究了苏-锡-常地区和上海市近30年由于抽水导致的区域地面沉降。其中的土体一维沉降模型可以考虑不同水文地质单元、不同应力期土体变形的弹性、弹塑性和黏弹塑性。HSI等[6](1994)应用有限元方法建立数学模型，研究土层内某点抽水引起的地面沉降，并比较了抽水时潜水位降低和不降低对地面沉降的影响。陈兴贤等[7](2013)建立了深基坑降水三维变参数非稳定渗流与太沙基一维固结理论的地面沉降耦合模型，采用有限元数值分析方法对模型进行求解，对南京地铁三号线浦珠路站深基坑降水进行了模拟计算。MIAO等[8](1991)建立了包含潜水层、弱透水层和抽水承压含水层的VEF模型和计算土体黏弹性变形的VES模型，将两者耦合并求解得出理论解析解。SU等[9](1998)针对单一潜水层内单井抽水建立柱坐标下的控制方程，其中假设土体应力应变符合线性关系，应用有限元方法求解地表面和土层内各点的变形。LOICIGA[10](2013)将地下水动力学与一维固结理论相结合，得出了单层承压含水层与潜水层抽水后地面沉降的理论解，对于多含水层情况则需要先借助于数值计算方法求解各含水层水位降深再累加获得地面沉降值。

理论解析法类型的文献，如COOKE[11]针对桩土荷载传递时考虑土体摩阻力影响提出了剪切位移法。原华等[12](2013)考虑地连墙和止水帷幕阻止土层变形的作用，提出一种侧摩阻力约束下降水引起的地面沉降估算方法。REN等[13](2014)借用矿业工程中预测地面沉降的影响函数法研究了潜水层抽水引起的地面沉降问题。

以上分层总和法与数值计算方法所得土层沉降预测值往往需要通过修正才可以获得接近沉降实测值的结果，理论解析法因假设条件严格而使其适用性有限。如果能像预测地下水位降深一样，通过若干抽水井周围区域实测点土层沉降而直接推算出距抽水井任意距离的地面沉降值，则既方便应用和操作，又提高了准确性，应是一种预测土层沉降的好方法。本文即是基于此目的研究这样一种方法。

1 理论论证

1.1 控制方程导出

抽水引起沉降的理论分析模型如图1所示。以抽水井为中心原点的柱坐标系中：变形范围内土体分为n层;r为距中心原点的距离，m;si为各层顶面位移值(取位移为0的面为第n层底面)，m；dwi为各层内水位降深值；Esi为各层的压缩模量，MPa；Gi为剪切模量，MPa；Mi为各层的土层厚度，m。

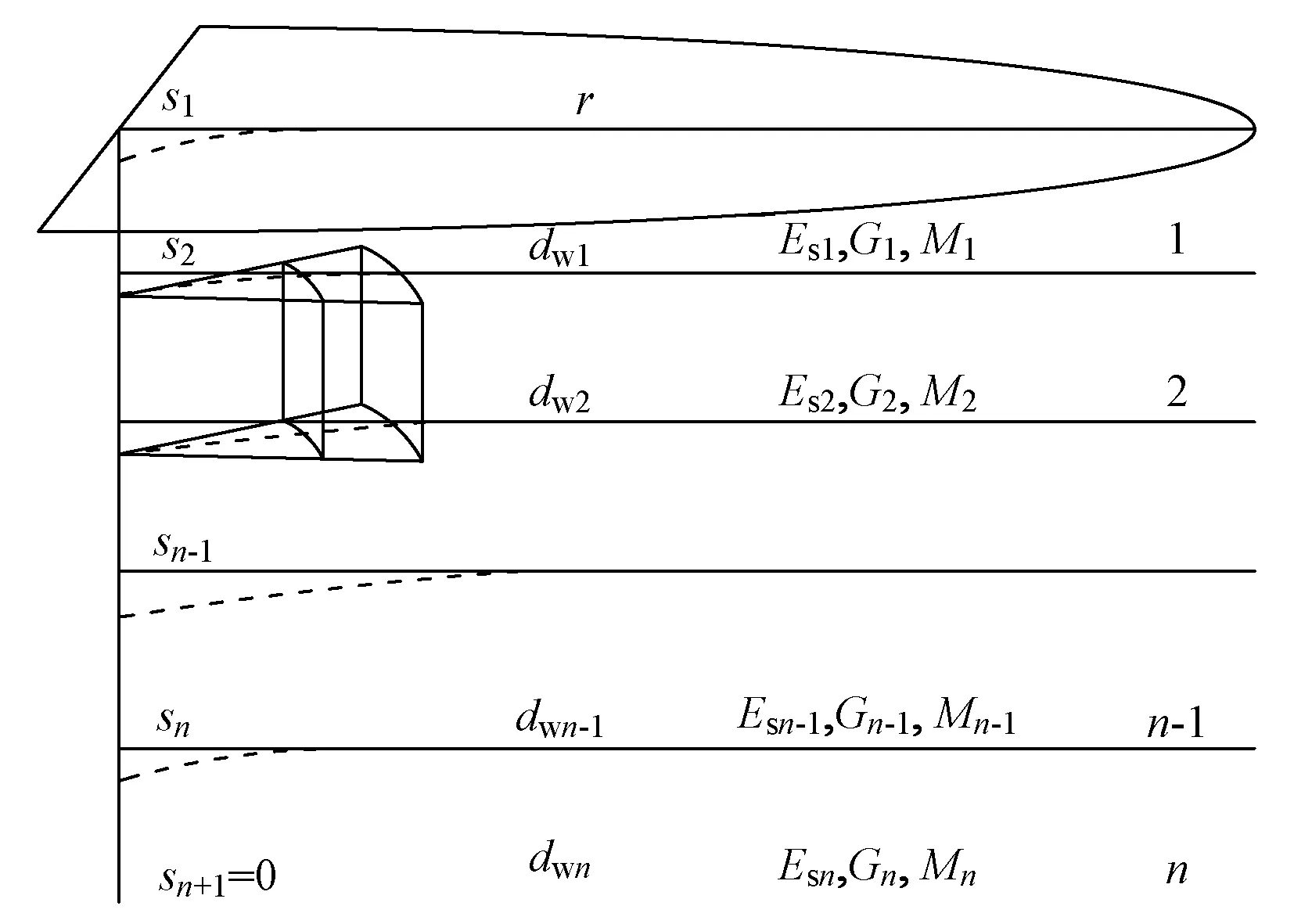
图1 抽水引起沉降的理论分析模型

基于以下假定，进行后面的理论分析：①各土层内土体均质、各向同性；②土体只发生竖向位移；③土体径向相邻两点的位移差引起摩阻力；④土体变形之应力应变满足线性关系。

以上假设③的合理性在于土层侧摩阻力在桩基工程中发挥重要影响。土体因位移差而产生摩阻力,这具有扎实的理论基础和广泛的工程应用。

土层压缩公式为[14]

(1)

式中：s为土层压缩量，可由土层上下表面位移差获得，m；M为土层厚度，m;Es为土层压缩模量，MPa；Δp为土层所受应力增量，kPa。

建筑物在地基中产生的附加应力，因荷载从上向下传递，随地基内深度增加而呈递减趋势。与之不同，抽水引起土层压缩，尤其是深层抽水引起土层压缩，类似采空区造成地面沉降。其荷载传递方向是从下往上，抽水处有效应力增加最大，而越往地面传递，水位降深越小，有效应力增加越小。所以抽水造成地面沉降应该考虑各土层尤其是上部土层摩阻力提供的抵抗下沉的作用。抽水导致土层沉降时若总应力不变，则应力增量Δp应由2部分组成，即水头降低导致的应力增量和径向相邻面相对位移导致的剪应力差值。其中前者导致土层有效应力增加，后者导致有效应力减小。表达式为

(2)

式中：rw为水的重度，kN/m3；dw为水位降深，m；τrz为剪应力，kPa；γrz为剪应变。

剪应力与剪应变及土层位移关系为[16]

τrz=Gγrz

(3)

(4)

当不考虑土体径向位移ur即土体只发生竖向沉降位移时，有

(5)

综合上述各式得土层沉降满足的公式为

(6)

将抽水区域土层分成n层，假设各土层上表面的位移值分别为s1,s2,…,sn，第n层下表面的位移值sn+1为0。由式(6)可得第1层、第2层、第i层、第n层的控制方程分别为

(9)

(10)

1.2 控制方程求解

先从第1层式(7)开始求解。该式为非齐次微分方程，先求解其齐次方程的一般解，再解其特解，则可得通解。

当dw1=0，即γwdw1=0，式(7)变为

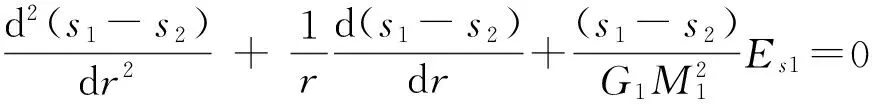
(11)

令

则式(11)变换为

(15)

方程两边同乘以x2得

(16)

令

将式(18)—式(23)代入式(16)得

(24)

式(24)为零阶Bessel方程，其通解为

y=c1J0(t)+c2Y0(t)

(25)

式中:c1,c2为任意常数;J0(t)为零阶第1类Bessel函数;Y0(t)为零阶第2类Bessel函数。

式(27)中ν是欧拉常数，通常取ν=0.577。

当t→0即井距r较小时

当井距r值较小且土层厚度M1值较大时，可按式(28)和式(29)计算J0(t)和Y0(t)，则通解式(25)变为

(30)

又有

(31)

式(31)中:μ为土的泊松比，通常取μ=0.3；E1为第1层土的弹性模量，土体弹性模量E1与压缩模量Es1之间是倍数关系[14]，MPa。

将式(12)—式(14),式(17)、式(31)代入式(30)可得

(32)

当t取值较大即井距r较大时

(33)

J0(t)→k

(34)

其中k为一常数且k<<1，则式(27)变为

(35)

则通解式(25)变为

(36)

(37)

由式(13)、式(14)、式(17)和式(31)可得

(38)

将式(12)、式(38)带入式(30)并化简得式(7)齐次方程的一般解

(39)

下面求抽水沉降分层计算公式(7)非齐次方程的特解。令

dw1≠0

(40)

设特解为

s1-s2=d1+d1lnr

(41)

式中:d1,d2为待定系数。

由式(41)得

(42)

式(7)变为

(43)

(44)

抽水时降深与井距间满足[17]

(45)

式中：sw1为抽水井中心水位降深，m；Q1为井抽水流量，m3/d；T1为导水系数，m2/d。

将式(45)代入式(44)得式(7)非齐次方程的特解为

(46)

(47)

取

(48)

(49)

得

s1-s2=c11+c12lnr

(50)

采用以上相同的求解方法可得第2层土层方程的解为

s2-s3=c21+c22lnr

(51)

同理可求得各土层方程的解为

(52)

1.3 地面沉降和分层沉降公式

下面进行抽水导致地面沉降及分层沉降分析。由以上分层公式(52)，等号两边累加得

s1=(c11+c21+…+cn1)+

(c12+c22+…+cn2)lnr

(53)

令

C11=c11+c21+…+cn1

(54)

C12=c12+c22+…+cn2

(55)

得地面沉降公式为

s1=C11+C12lnr

(56)

式(52)中有

s1-s2=c11+c12lnr

(57)

得

(58)

同理可得各分层沉降值为

(59)

以上式(56)和式(59)表明由抽水引起的土层地面沉降与井距呈半对数线性关系。

2 工程实例验证

选取抽水导致土层地面沉降的第三方实测数据对本文以上分析结果进行验证。实例一、实例二和实例三分别为国外文献[2]、国内台湾文献[16]和国内大陆文献[18]的资料。

2.1 理论解验证

文献[15]建立了由于抽水导致区域性地面沉降的数学模型，经过一系列推导给出了抽水引起的地面沉降计算的理论解。本文利用其给出的理论解，采用文献中给出的例子对式(56)进行验证。

文献中给出了抽水导致的区域性地面沉降公式。单井抽水引起的沉降公式为

(60)

群井(分布呈圆形)抽水引起的沉降公式：

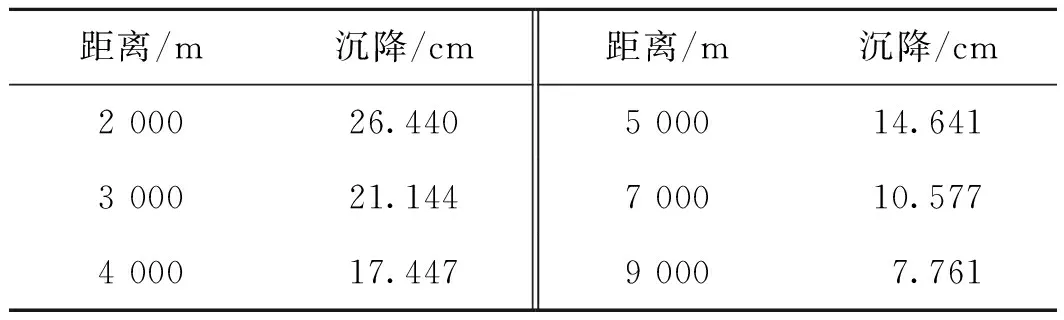
当t>0.4r2/Cν且r

(61)

当t>0.4r2/Cν且r>R时

(62)

式中：t为沉降时间；Qw为单位时间内的抽水量；Cν为固结系数；r为测点到沉降中心的距离；W()为泰斯井流的井函数；R为抽水井的分布半径；∑Qw为圆形区域内所有井单位时间内的总抽水量。

选取文献中的实例，利用其理论解分别进行单井、群井抽水导致地面沉降的验证。群井抽水井分布如图2 所示。抽水井呈圆形分布，分布半径为R。

图2 抽水井分布

验证步骤：①利用上述单井公式式(60)、群井公式式(61)、式(62)分别计算标注线上一系列观测点的沉降值，列于表1、表2。②拟合直线上的s-lnr半对数曲线得拟合参数c1,c2值及相关系数。相关参数的取值：Cv=6×103cm2/s;∑Qw=500 L /s;r=3.0 km;R=1.5 km;t=5 a.

表1 单井抽水下不同距离处的沉降

表2 群井抽水下不同距离处沉降

利用经典理论解计算的由于抽水导致的地面沉降s和测点到沉降中心的距离r的关系为：①单井降水下s=180.034-12.589lnr，相关系数99.92%;②群井降水下s=178.220-12.451lnr，相关系数99.91%。关系式符合半对数线性关系，很好地论证了式(56)。

2.2 工程实例一

工程实例一源自文献[2]，工程地点位于美国西南部(The Mesquite,Nevada)，在一个新建的市政工程井内放置抽水泵进行含水层抽水与地表位移监测试验。试验井穿过500 m厚的冲积土层，抽水试验持续62 d。图3为抽水井和观测点布置以及观测点由于抽水引起的地面水平变形。

图3 抽水井与沉降监测点布置

观测点的水平位移和地面沉降采用GPS技术测量，地面沉降测量精度达到2 mm。WX31为试验抽水井，VT01—VT10为观测点，VT14为试验参考点即测量基准站。文中所有测量的位移是相对于抽水井西 2 000 m 的基准站(VT14)，经过62 d抽水试验之后得到各个观测点地面沉降数据,列于表3。

表3 地面沉降与到抽水井距离汇总

经拟合得实测沉降值s与距离对数值lnr间函数关系,见式(63)，线性相关系数为99.66%。

s1=3.85lnr-29.83

(63)

2.3 工程实例二

工程实例二源自文献[16]，试验场地位于中国台湾台中港附近平坦的沙区，抽水井滤水管段分别穿过砂质粉土层(埋深5～15 m)、淤泥层(埋深15～25 m)、粉砂质黏土层(埋深25～35 m)和砂质粉土层(埋深35 m 以下)等地层。试验场地距离台中市21 km，距离彰化市17 km，距离海岸约500 m。该工程为单井抽水试验，抽水井布置在试验场地中心，抽水井周围设置水准测量点以监测地面竖向沉降，布置7口水位监测井以监测地下水位变化。图4为抽水井和沉降监测点布置。

图4 抽水点与沉降监测井布置(据文献[16],单位：m)

试验采用不同的抽水速率Q1=200 L/min,Q2=320 L/min和Q3=400 L/min，待地面沉降稳定后获得各观测点沉降数据，列于表4。经拟合得实测沉降值s与距离对数值lnr间函数关系式列于表5，关系曲线见图5,线性相关度分别为95.89%,94.45%和97.38%。需要说明的是，沉降监测数据中距抽水井最近点r=2 m处的沉降值较其他观测数据相差太大，其原因是监测点距离抽水井太近，土体水平位移影响地面竖向沉降。

表4 地面沉降与到抽水井距离汇总

表5 沉降值s与距离对数值ln r间函数关系式汇总

图5 s-ln r关系曲线

2.4 工程实例三

工程实例三源自文献[18]，天津西站交通枢纽建设工程位于红桥区。该试验为承压水非稳定流抽水试验，试验中监测抽水引起的地面沉降，抽水试验含水层位于埋深15～46 m土层内。抽水井滤管段穿过粉质黏土层(埋深15～22 m)、粉土层(埋深22～34 m)和黏土层(埋深30～46 m)，试验场地布置如图6所示。K1,K2,K3为抽水试验井并且分布在以D1为圆心的圆周上，D1—D10为地面沉降观测点。K1,K2,K3群井抽水持续7 d，每日出水量为799.2 m3。群井抽水试验开始的同时，对抽水井附近区域进行了地面沉降监测，各测点到井群中心距离与实测地面沉降值见表6。经拟合得实测沉降值s与距离对数值lnr间函数关系为式(61)，线性相关系数为98.10%，见图7。

图6 抽水井与沉降监测点布置

测点沉降/mm距离/mD1-13.80 D2-15.83.30D3-12.18.74D4-11.313.68D5-9.518.71D6-7.123.81D7-5.729.52D8-4.136.72D9-4.343.54D10-3.650.76

图7 s-ln r关系曲线

3 结论

本文针对抽水导致地面和土层沉降这一热点问题，经过合理假设和严格数学推导，得出地面沉降与井距呈半对数线性关系的规律，即s1=C11+C12lnr。

利用经典理论解计算的由于抽水导致的地面沉降s和测点到沉降中心的距离r的关系在单井降水下相关度为99.92%，在群井降水下为99.91%，符合半对数线性关系。经美国、台湾和天津3个实际抽水的5组地面沉降监测实例数据拟合，抽水引起的地面沉降和井距间半对数线性规律亦得到极好验证，线性相关度分别为99.66%,95.89%,94.45%,97.38%和98.10%。该规律可用于预测距抽水井任意距离区域的地面沉降值，具有广泛应用价值。

需要说明，如果土层条件不满足本文假设条件，尤其是工程场地地下结构物较多、干涉较大时，将影响以上规律的使用。另本文方法主要应用于抽水引起的地面竖向沉降计算，当抽水导致地下水力梯度较大时，土层存在水平向变形。该方法不适用于水平向变形计算。

[1]曹文贵,邓湘君,张超.基于Duncan-Chang 模型的地基沉降分层总和分析方法探讨[J].岩土工程学报,2013,35(4):643-649.

[2]BURBEY T J,WARNER S M,BLEWITT G,et al.Three-dimensional Deformation and Strain Induced by Municipal Pumping,Part 1:Analysis of Field Data[J].Journal of Hydrology,2006,319(1-4):123-142.

[3]BURBEY T J.Three-dimensional Deformation and Strain Induced by Municipal Pumping,Part 2:Numerical Analysis[J].Journal of Hydrology,2006,330(3-4):422-434.

[4]KIHM J H,KIM J M,SONG S H,et al.Three-dimensional Numerical Simulation of Fully Coupled Groundwater Flow and Land Deformation due to Groundwater Pumping in an Unsaturated Fluvial Aquifer System[J].Journal of Hydrology,2007,335(1):1-14.

[5]SHI X Q,WU J C,YE S J,et al.Regional Land Subsidence Simulation in Su-Xi-Chang Area and Shanghai City,China[J].Engineering Geology,2008,100(1-2):27-42.

[6]HSI J P,CARTER J P,SMALL J C.Surface Subsidence and Drawdown of the Water Table due to Pumping[J].Geotechnique,1994,44(3):381-396.

[7]陈兴贤，骆祖江，安晓宇，等.深基坑降水三维变参数非稳定渗流与地面沉降耦合模型[J].吉林大学学报(地球科学版)，2013，43(5)：1572-1578.

[8]MIAO J F,WU L G.Mathematical Modelling of Land Subsidence due to Pumping of a Multi-aquifer System with Viscoelastic Properties[C]//Proceedings of the Fourth International Symposium on Land Subsidence,IAHS,1991.

[9]SU M B,SU C L,CHANG C J,et al.A Numerical Model of Ground Deformation Induced by Single Well Pumping[J].Computers and Geotechnics,1998,23(1-2):39-60.

[11]史佩栋.桩基工程手册[M].北京:人民交通出版社,2008.

[12]原华,张庆贺,张建伟.侧摩阻力约束下降水引起的地面沉降估算方法[J].上海交通大学学报,2013,47(8):1329-1334.

[13]REN G,BUCKERIDGE J,LI J.Estimating Land Subsidence Induced by Groundwater Extraction in Unconfined Aquifers Using an Influence Function Method[J].Journal of Water Resources Planning and Management,2014,141(7):1-10.

[14]东南大学，浙江大学，湖南大学，等.土力学[M].北京：中国建筑工业出版社,2008.

[15]BEAR J,CORAPCIOGLU M Y.Mathematical Model for Regional Land Subsidence due to Pumping:1.Integrated Aquifer Subsidence Equations Based on Vertical Displacement Only[J].Water Resources Research,1981,17(4):937-946.

[16]SU M B,SU C L,CHANG C J,et al.A Numerical Model of Ground Deformation Induced by Single Well Pumping[J].Computers and Geotechnics,1998(23):39-60.

[17]徐芝纶.弹性力学[M].北京：高等教育出版社,2002.

[18]罗建军,瞿成松,武永霞,等.天津西站交通枢纽配套市政公用工程水文地质抽水试验报告[R].上海：上海长凯岩土工程有限公司,2009.