城市轨道交通简支梁桥墩顶纵向刚度限值研究

赫腾飞，赵文娟

(河北建筑工程学院 土木学院，河北 张家口 075000)

铁路桥梁上铺设无缝线路具有改善桥梁和轨道的运营状态、减少养护维修工作量、延长线路及桥梁使用寿命等优点，为此国内外研究人员对桥上无缝线路设计理论、梁轨相互作用机理等方面进行了较多研究[1-4]。由于城市轨道交通高架桥上一般铺设无缝线路，相关研究人员也对城市轨道交通桥上无缝线路进行了研究[5-6]。桥墩线刚度合理取值是桥上无缝线路设计的关键技术之一[5]，因此桥上无缝线路必须确定桥墩最小纵向刚度，保证钢轨应力或梁轨相对位移不超过允许范围，确保轨道结构的安全可靠。

我国《地铁设计规范》(GB 50157—2013)规定采用无缝线路时高架简支梁桥的墩顶纵向刚度最小应满足表1的要求，单线桥梁的桥墩纵向刚度取表中数值的1/2。从表1可知，对于20 m和21 m跨度的简支梁桥，最小水平刚度分别为240 kN/cm和320 kN/cm，相差80 kN/cm，但钢轨附加应力相差不大。增大桥梁墩顶纵向刚度，将增加工程造价，因此文献[7]认为该墩顶最小纵向刚度不合理，并提出采用梁轨相互作用研究确定高架桥墩顶纵向刚度限值，然而未对桥墩纵向刚度限值的控制指标和限值进行研究。

本文以城市轨道交通常用的30 m简支槽形梁为例，基于梁轨相互作用原理，建立桥上无缝线路计算模型，分析不同墩顶纵向刚度对桥上无缝线路受力特性的影响规律，根据控制指标确定墩顶纵向刚度限值，从而为其他城市轨道交通高架桥墩顶纵向刚度限值的制定提供参考。

表1 桥墩墩顶纵向水平线刚度(双线)

注：不设钢轨伸缩调节器。

1 计算模型及参数

1.1 计算模型

考虑线路横向对称，取1股钢轨作为研究对象，建立线-桥-墩一体化计算模型，如图1所示。

图1 桥上无缝线路计算模型

模型中，钢轨和桥梁均采用梁单元模拟，钢轨在纵向按扣件间距划分单元，其节点与桥梁节点通过弹簧连接。由于城市轨道交通简支梁上轨道结构一般采用无砟轨道结构，轨道结构与桥面采用强连接，轨道的纵向阻力主要由扣件系统提供，扣件系统采用非线性弹簧模拟。桥墩处约束其垂向位移，对于固定支座，建立纵向线性弹簧，弹簧刚度取为墩顶纵向刚度。为消除边界条件的影响，模型中桥梁两侧各建立100 m长的路基地段。

1.2 计算参数

线路设计速度为100 km/h，根据GB 50157—2013的相关规定，曲线半径为400 m，线路的最大坡度为30‰，在制动力计算中考虑坡度的影响。线路设计超高120 mm，未被平衡超高75 mm。

钢轨采用60 kg/m钢轨，扣件采用DTⅦ 2型扣件，垂向静刚度为25～35 kN/mm，扣件系统纵向阻力采用双线性阻力模拟，无车时取每根轨8.3 kN/m，有车时取每根轨12.865 kN/m，极限位移为0.5 mm。取20跨30 m简支槽形梁建模，桥梁的参数见文献[8]，桥台刚度取为双线 3 000 kN/cm，固定支座在桥梁左端。

车辆采用地铁A型车，动力系数取为0.8，则列车竖向活载可采用长度132.2 m、大小为50.53 kN/m的均布荷载模拟。为反映线路坡度的影响，制动或启动时的轮轨黏着系数取0.164+i[9]，i为线路坡度。

2 纵向刚度限制指标

1)钢轨强度

根据《铁路无缝线路设计规范》(TB 10015—2012)中规定的钢轨强度检算标准为

(1)

式中：σd为动弯应力;σt为钢轨最大温度应力;σf为钢轨最大附加应力;σz为钢轨牵引(制动)应力;[σ]为钢轨容许应力;σs为钢轨屈服强度;K为安全系数，取为1.3，因此钢轨的容许应力为351.5 MPa。

根据上述计算参数，计算得到钢轨的轨头压应力为163.81 MPa，轨底拉应力为127.12 MPa。当钢轨轨温变化幅度分别为30，40,50 ℃时，钢轨附加纵向力限值分别为877.4，685.4,493.3 kN。

2)梁轨(板)相对位移

为保证轨下胶垫的正常使用以及扣件系统的稳定性，在制动(牵引)下钢轨与轨道板间的相对位移不大于4 mm[10]。

3)钢轨断缝值

GB 50157—2013规定：对于无砟轨道，钢轨断缝允许值为100 mm。

3 计算结果及分析

为确定简支梁桥墩顶纵向刚度的限值，本文研究了不同墩顶纵向刚度对桥上无缝线路受力特性的影响规律，墩顶纵向刚度分别取为100，150，200，250，300，350，400，450，500 kN/cm。

3.1 伸缩工况

当桥梁升温30 ℃时，随着墩顶纵向刚度的增大，钢轨伸缩附加力增大。当墩顶纵向刚度为100 kN/cm时，钢轨最大伸缩附加力为104.99 kN;墩顶纵向刚度增大至500 kN/cm时，钢轨最大伸缩附加力为142.75 kN，增大35.96%。

由于桥梁的抗弯刚度较大，钢轨挠曲附加力远小于钢轨伸缩附加力，因此挠曲附加力在钢轨强度控制中不起作用，故本文未分析墩顶纵向刚度对钢轨挠曲附加力的影响。

3.2 制动工况

列车从左侧入桥，分别考虑单线和双线制动，不同制动情况下钢轨制动附加力如图2所示，梁轨(板)相对位移如图3所示。

图2 钢轨制动附加力

图3 梁轨(板)相对位移

从上图可知，随着墩顶纵向刚度的增大，钢轨最大制动附加力和梁轨(板)相对位移均减小。当单线制动时，纵向刚度为100 kN/cm时，钢轨最大制动附加力为306.54 kN，梁轨(板)相对位移为3.58 mm;桥墩刚度为500 kN/cm时，钢轨最大制动附加力和梁轨(板)相对位移分别为182.07 kN，1.36 mm，分别降低40.60%，62.01%。当双线制动时，纵向刚度为100 kN/cm 时，钢轨最大制动附加力为361.29 kN，梁轨(板)相对位移为4.92 mm;桥墩刚度为500 kN/cm时，钢轨最大制动附加力和梁轨(板)相对位移分别为233.79 kN，2.14 mm，分别降低35.29%,56.50%。

3.3 断轨工况

钢轨断缝值随墩顶纵向刚度的增大而减小[1]，本文计算得到桥墩刚度为100 kN/cm，钢轨降温50 ℃时的断缝值仅为75 mm，远小于钢轨断缝限值，故钢轨断缝值不是限制墩顶纵向刚度限值的控制指标。

3.4 墩顶纵向刚度限值

考虑最不利的情况，即伸缩附加力与双线制动共同作用，此时不同墩顶纵向刚度下的钢轨附加力、梁轨(板)相对位移如图4所示。

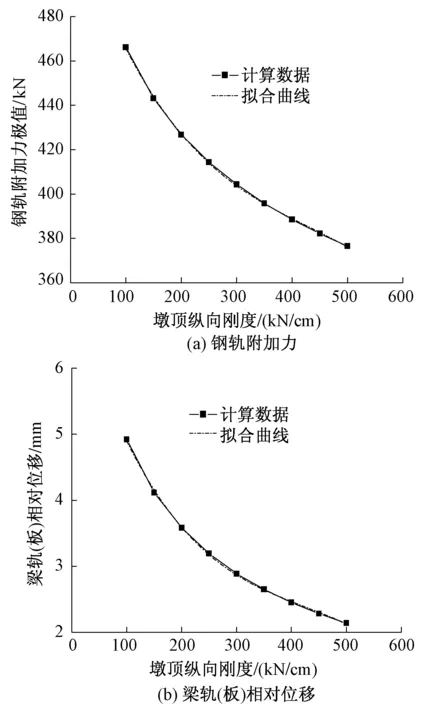
图4 钢轨纵向力附加力极值

从图4可知，钢轨纵向附加力极值和梁轨(板)相对位移均随着桥墩刚度的增加而减小。钢轨纵向附加力、梁轨(板)相对位移与墩顶纵向刚度的关系曲线可以拟合为

F=526.114-0.734 6K+0.001 42K2-

1.099 3×10-6K3,R=0.999 6

(2)

w=7.046 6-0.026 57K+0.000 06K2-

4.346 8×10-8K3,R=0.999 5

(3)

式中：F为钢轨纵向附加力极值,kN;w为梁轨(板)相对位移,mm;K为桥墩刚度,kN/cm。

当桥墩墩顶纵向刚度为100 kN/cm时，钢轨附加力最大值为466.29 kN，仍小于轨温变化50 ℃时的附加力限值493.3 kN，而梁轨(板)相对位移为4.92 mm，大于相关规定的4 mm。可见对于简支梁桥，控制桥墩纵向刚度的主要指标是梁轨(板)相对位移。

当以梁轨(板)相对位移为4 mm作为控制指标时，根据式(3)可得墩顶纵向刚度限值为180 kN/cm。考虑一定的安全余量，建议城市轨道交通30 m简支梁桥的墩顶纵向刚度限值为240 kN/cm。

基于梁轨相互作用原理计算得到的桥墩纵向刚度小于规范规定的限值，这也说明了规范规定的限值较严，将增加工程造价。建议结合工程实践，根据实际参数，研究确定城市轨道交通简支梁桥的最小纵向刚度限值。

4 结论

本文通过建立30 m简支梁桥上无缝线路计算模型，以钢轨强度、梁轨(板)相对位移和断缝值作为控制指标，研究不同墩顶纵向刚度对桥上无缝线路受力特性的影响规律，提出了城市轨道交通简支梁桥墩顶纵向刚度限值，得到如下结论：

1)随着墩顶纵向刚度的增大，钢轨伸缩附加力增大，钢轨制动附加力和梁轨(板)相对位移降低；

2)对于简支梁桥，控制墩顶纵向刚度限制的指标有钢轨强度、梁轨(板)相对位移和钢轨断缝值，其中梁轨(板)相对位移起决定作用；

3)为降低工程造价，可基于梁轨相互作用原理确定桥墩纵向刚度限值，考虑一定的安全余量，建议30 m 简支梁桥的墩顶纵向刚度限值为双线240 kN/cm。

[1]王平,肖杰灵,陈嵘,等.高速铁路桥上无缝线路技术[M].北京:中国铁道出版社,2016.

[2]CZYCZULA W,SOLKOWSKI J,TOWPIK K.Interaction Between CWR Track and Bridge in Longitudinal Direction[J].Archives of Civil Engineering,1997,43(1):51-69.

[3]广钟岩.铁路无缝线路[M].北京:中国铁道出版社,2001.

[4]魏峰,牛斌,季文玉.客运专线铁路简支梁桥墩台纵向线刚度分析研究[J].铁道建筑，2010,50(4):21-25.

[5]李秋义,陈秀方.城轨高架桥上无缝线路设计的关键技术[J].城市轨道交通研究,2004,7(2):83-86.

[6]曲村,高亮,侯博文.城市轨道交通长大桥梁上无缝线路钢轨制动力研究[J].城市轨道交通研究,2012,15(10):66-70.

[7]马坤全,陈宇,潘湘文.轨道交通U型梁桥下部结构纵向水平线刚度合理值研究[J].城市轨道交通研究,2010,13(1):36-40.

[8]文志云,刘兰.上海轨道交通6号线高架区间30 m简支槽型梁设计简介[J].现代城市轨道交通,2005,8(1):28-30,40.

[9]颜乐,熊震威,魏贤奎,等.坡度对长大坡道桥上无缝道岔的影响分析[J].铁道标准设计,2013,57(9):33-36.

[10]UIC.UIC 774-3 Track/bridge Interaction.Recommendations for Calculations[S].Paris:International Union of Railways,2001.