基于交互式多模型的双站高频地波雷达机动目标跟踪算法❋

张 玲, 李英帅， 牛 烔， 王 琨

(中国海洋大学工程学院，山东省高校海洋机电装备与仪器重点实验室 山东 青岛 266100)

高频地波雷达[1]可以探测海上的超视距目标，因此也被称为超视距雷达。但是该雷达的测向精度较低，容易导致目标跟踪精度降低。同时，随着科技的发展和现实的需求，雷达的小型化变得尤为重要，这样便使得雷达天线尺寸受到限制，从而会进一步影响侧向精度。因此，在角度信息不精确的情况下，更好的跟踪到目标具有极为重要的实际意义。付天娇等人[2]提出了一种无角度双站式高频地波雷达系统，与传统的单站式高频地波雷达系统相比,仅利用两个雷达站观测的径向距离和径向速度信息进行跟踪，并保证了良好的跟踪精度。但是在实际中，海面上的目标可能会发生多种机动情况[3]，因此，研究该雷达的机动目标跟踪问题具有使用价值。

描述目标运动情况的模型主要有匀速(CV)模型、匀加速(CA)模型、匀速转弯(CT)模型、singer模型、“当前”统计模型等。考虑到海面上的目标多为匀速运动，机动性主要体现为运动轨迹的形变，因此本文主要以海面上的匀速运动船只作为研究对象，其运动过程主要为直线运动和转弯运动的交替变换，并在双站式高频地波雷达背景下进行跟踪。因此，传统的单一模型跟踪算法将不再适用。

在机动目标跟踪领域，交互式多模型(Interacting Multiple Model，IMM)算法[4-6]有着广泛应用。IMM算法具有一定的自适应性，能够实时在线调整各个模型的概率，并依据此概率进行估计值的加权求和，实现目标的机动跟踪。一个完整的IMM滤波器包括：输入交互作用器，各模型对应的滤波器，各模型概率更新器以及输出混合作用器。同时建立的每个模型均为非线性模型，因此各模型对应的滤波器采用扩展卡尔曼滤波[7](Extended Kalman Filter，EKF)，EKF算法通过求取模型方程中的非线性项的一阶泰勒展开，来进行模型的线性化，然后利用经典的Kalman滤波公式进行状态估计。

1 系统模型建立

无角度双站式高频地波雷达的原理见图1，假设目标与两个雷达站在同一个平面上，且运动目标始终在2个雷达站的一侧。

图1 双站式高频地波雷达定位与跟踪原理图

目标的运动模型由状态模型和量测模型[8-9]表示，在本文中，分别表示为

X(k+1)=A·X(k)+B·Γ(k)，

(1)

Z(k+1)=H(X(k+1))+O(k+1)，

(2)

式中：k表示采样时刻；X(k)和Z(k)分别代表状态向量和观测向量；A和B分别是系统的转移矩阵和系统噪声的转移矩阵；Γ(k)和O(k)分别是均值为0的高斯白噪声。

本文中描述的目标主要有两种运动状态：匀速运动(CV)、匀速转弯运动(CT)。在模型中，x和y代表位置信息，vx和vy代表速度信息，ω表示转弯速率。

对于CV模型，状态向量为

则CV模型的状态方程为

X(k+1)=ACV·X(k)+BCV·ΓCV(k)。

(3)

式中

(4)

(5)

过程噪声ΓCV(k)=[τx(k),τy(k)]T，其中τx(k)、τy(k)是相互独立且均值为0的高斯白噪声。

对于CT模型，状态向量为

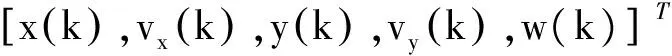
则CT模型的状态方程为

X(k+1)=ACT·X(k)+BCT·Γ(k)。

(6)

式中

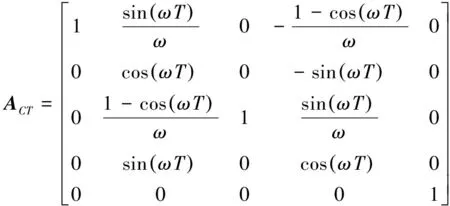
(7)

(8)

过程噪声ΓCV(k)=[τx(k),τy(k),τω(k)]T，其中τx(k)、τy(k)、τω(k)是相互独立且均值为0的高斯白噪声。

对于观测模型，d1和v1代表雷达1观测的径向距离和径向速度，d2和v2代表雷达2观测的径向距离和径向速度，则观测方程为

(9)

式中

(10)

观测噪声为

O(k+1)=[od1(k+1),ovd1(k+1),od2(k+1),ovd2(k+1)]T。

其中，od1(k+1)、ovd1(k+1)、od2(k+1)、ovd2(k+1)是相互独立且均值为0的高斯白噪声。

但是，由于双站式高频地波雷达系统中2个雷达站是独立进行观测的，当海面上存在多个目标时，会出现大量的虚假目标，如果有n(n≥2)个目标，则会出现n2-n个虚假目标，当对多目标进行跟踪时，如何排除虚假目标也存在重要意义，但是本文只讨论在单目标跟踪情况下的机动目标跟踪问题。

2 IMMEKF算法

在整个运动过程中，每个运动时刻的运动模型均是非线性的，因此在IMM算法中采用最常用的非线性估计方法即扩展卡尔曼滤波(EKF)算法[10]。EKF算法是将模型方程中的非线性部分展开成泰勒级数，并略去二阶及以上高阶项来进行近似线性化，得到非线性系统的线性化模型。该方法在实际中应用广泛且滤波精度较高。

2.1 EKF算法

对于双站式地波雷达系统，观测方程中的H(X)是非线性函数，并且CT模型中的ACT含有ω项，因此ACTX也是关于X的非线性函数。则EKF滤波公式[11]为

(11)

(12)

(13)

(14)

(15)

P(k+1|k)=F(k)P(k,k)FT(k)+B·Q(k)·BT，

(16)

S(k+1)=H(k+1)P(k+1|k)HT(k+1)+R(k+1)，

(17)

K(k+1)=P(k+1|k)HT(k+1)S-1(k+1)，

(18)

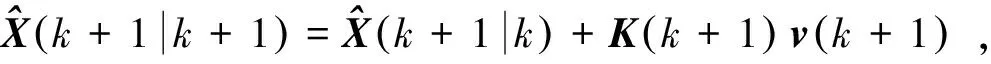
(19)

P(k+1|k+1)=[I-K(k+1)H(k+1)]P(k+1|k)。

(20)

2.2 IMMEKF算法

假设整个运动过程可以用r个模型表示，其状态方程为

Xj(k+1)=Aj·Xj(k)+Bj·Γj(k),j=1,2,…,r

(21)

模型之间的转换满足马尔科夫过程，且转移矩阵为

(22)

具体算法步骤[12]如下：

步骤1 算法初始化

(23)

模型的混合概率为

(24)

对模型j混合估计，重新初始化状态和协方差的混合估计

(25)

(26)

步骤2 匹配各个模型的滤波器

步骤3 模型概率更新

模型j在k+1时刻的概率为

(27)

其中

(28)

(29)

步骤4 估计融合

在k+1时刻的总体估计和总体估计误差协方差阵为

(30)

(31)

在本文中描述的目标运动主要包括CV和CT两种模型，综合上述公式(11)～(31)得到IMM算法的流程如图2所示。

3 仿真

为了验证算法的性能，与单模型的跟踪算法进行比较，做如下仿真实验。在双站式高频地波雷达的观测背景下，假设目标的初始位置为(26 km,26 km)，初始速度为(15m/s,15m/s)，雷达的采样周期为10s，在0～30,60～90,120～150周期内做匀速运动，是CV模型；在30～60,90～120周期做匀速转弯运动，是CT模型。在仿真中，为了验证IMM算法的性能，将分别基于CV和CT的单模型算法和IMM算法进行比较，在相同的初始条件下进行了50次Monte Carlo仿真，并求取各项指标的均方根误差(RMSE)，具体结果如图所示。

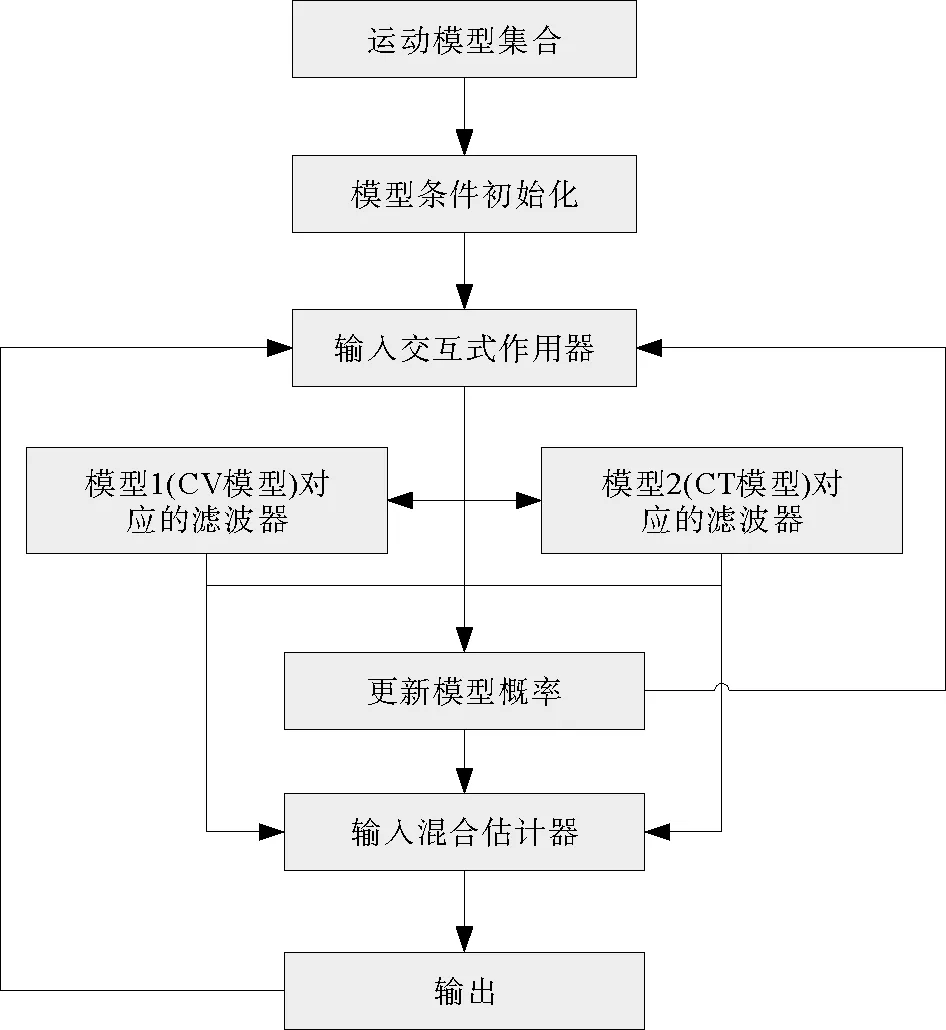
图2 IMM算法流程图

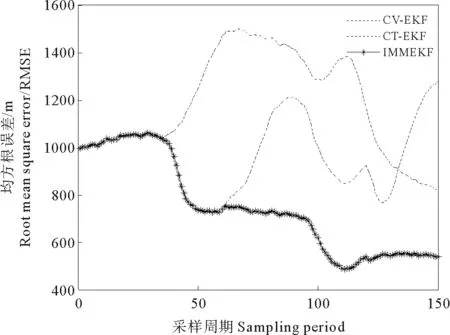
图3 目标位置的RMSE曲线

图3是三种算法的位置跟踪RMSE曲线；图4和5是3种算法的速度跟踪RMSE曲线。从图3中可以看出，初始时刻的误差较大，在整个跟踪过程中IMMEKF算法的误差逐渐减小，并且在50个周期后，跟踪精度已经明显高于其他两种算法；在稳定方面，CV-EKF和CT-EKF已经出现有了明显的发散迹象，而本

图4 目标在X轴上的速度RMSE曲线

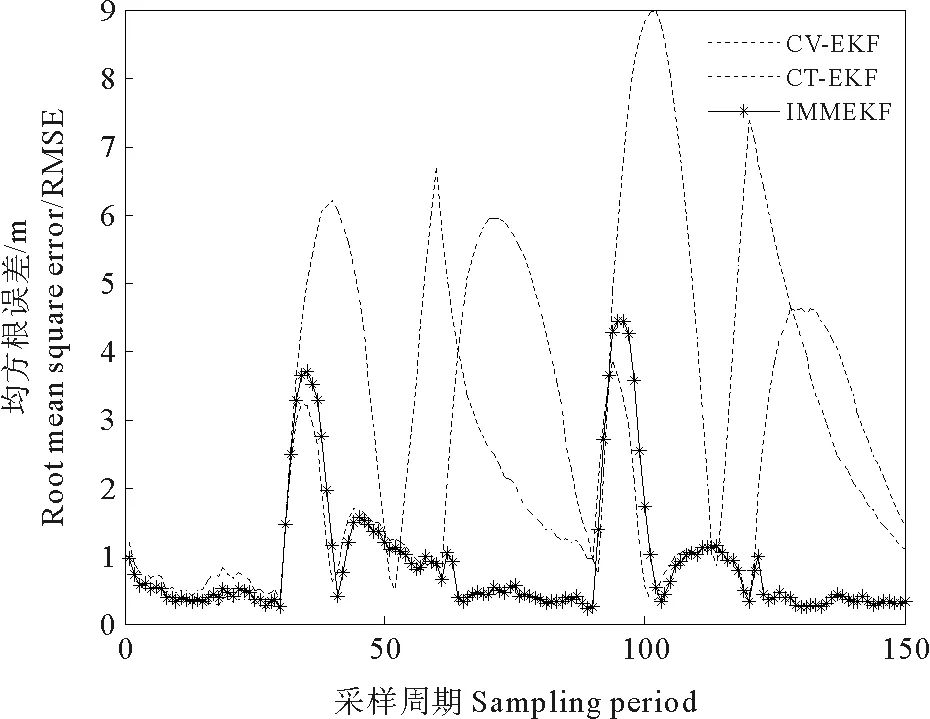
图5 目标在Y轴上的速度RMSE曲线

图6 目标的转弯角速度曲线

文中的算法且保持了良好的稳定性。从图4和5中看出，在目标机动时，三者的在X轴和Y轴上的速度估计都会发生较大偏差，但是IMMEKF算法可以更快的稳定下来，并保持误差较小。从图6中看出，对于角速度的估计，IMMEKF算法也是最优的。因此，对于各项指标，IMMEKF均要优于其他两种算法。

4 结语

本文利用交互式多模型(IMM)算法对无角度双站式地波雷达机动目标跟踪进行了研究。首先依据无角度双站式地波雷达的特点，建立了相应的CV模型、CT模型，将IMM算法和EKF算法相结合并应用到运动目标的跟踪中。在仿真过程中，与基于单一CV模型和CT模型的EKF算法进行比较，结果表明，IMM算法比单模型跟踪算法的跟踪精度要高，并且稳定性要好。因此，应用IMM-EKF算法可以更好的解决双站式地波雷达中的机动目标跟踪问题。

[1] 刘春阳, 王义雅. 高频地波超视距雷达述评[J]. 现代防御技术, 2002, 30(6): 38-46.

Liu C, Wang Y. Review on high frequency ground wave over-the-horizon radar[J]. Modern Defence Technology, 2002, 30(6): 38-46.

[2] 付天骄, 周共健, 田文龙, 等. 无角度双站地波雷达组合定位跟踪和滤波算法[J]. 系统工程与电子技术, 2011, 33(3): 552-556.

Fu T, Zhou G, Tian W, et al. HFground wave bi-station radar tracking and filteringwithout azimuthal measurements[J]. Systems Engineering and Electronics, 2011, 33(3): 552-556.

[3] 魏巍, 朱东旭, 陈兴. 基于交互式多模型算法的地面机动目标运动模型研究[J]. 计算机测量与控制, 2013, 21(5): 1348-1350.

Wei W, Zhu D, Chen X. Study on Motion Model of targets Based on Interactive Multiple Model Algorithm[J]. Computer Measurement & Control, 2013, 21(5): 1348-1350.

[4] Besada JA. Design of IMM filter for radar tracking using evolution strategies[J]. Ieee Transactions on Aerospace and Electronic Systems, 2005, 41(3): 1109-1122.

[5] Seah CE, Hwang I. Algorithm for Performance Analysis of the IMM Algorithm[J]. Ieee Transactions on Aerospace and Electronic SystemS, 2011, 47(2): 1114-1124.

[6] 宫淑丽, 王帮峰, 吴红兰, 等. 基于IMM算法的机场场面运动目标跟踪[J]. 系统工程与电子技术, 2011, 33(10): 2322-2326.

Gong S, Wang B, Wu H, et al. tracking of moving targets on airport surface based on IMM algorithm[J]. System Engineering and Electronics, 2011, 33(10): 2322-2326.

[7] Zhan P, Casbeer D W, Swindlehurst A L. Adaptive Mobile Sensor Positioning for Multi-Static Target Tracking[J]. Ieee Transactions on Aerospace and Electronic Systems, 2010, 46(1): 120-132.

[8] 程咏梅. 基于推广卡尔曼滤波的多站被动式融合跟踪[J]. 系统仿真学报, 2003, 15(04): 548-550.

Cheng Y. Multistation Passive Fusion Tracking Based on Extended KalmanFilter[J]. Journal of System Simulation, 2003, 15(04): 548-550.

[9] Stancic R, Graovac S. The integration of strap-down INS and GPS based on adaptive error damping[J]. Robotics and Autonomous Systems, 2010, 58(10): 1117-1129.

[10] Toledo-Moreo R. High-integrity IMM-EKF-based road vehicle navigation with low-cost GPS/SBAS/INS[J]. Ieee Transactions on Intelligent Transportation Systems, 2007, 8(3): 491-511.

[11] 潘丽娜. 基于扩展卡尔曼滤波的多传感器目标跟踪[J]. 舰船电子工程, 2010, 30(12): 71-72.

Pan L. Multisensor Multitarget Tracking Fusion Algorithms Based on EKF[J]. Ship Electronic Engineering, 2010, 30(12): 71-72.

[12] 李世忠, 王国宏, 吴巍, 等. IMM-EKF雷达与红外序贯滤波跟踪机动目标[J]. 火力与指挥控制, 2012, 37(1): 39-42.

Li S, Wang G, Wu W, et al. Research on Maneuvering Target Tracking Via Infrared Sensorand Radar Sequence Filtering Based on IMM-EKF[J]. Fire Control & Command Control, 2012, 37(1): 39-42.