城市物流配送车辆调度模型及优化

卢军莉，傅忠宁，李金萍 LU Junli,FU Zhongning,LI Jinping

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

0 引言

车辆路径问题（Vehicle Routing Problem，VRP） 最早是由Dantzig和Ramser[1]于1959年首次提出，是指拥有一定量的客户数，各自都具有不同数量、不同品种的货物需求，物流配送中心向需求客户提供货物，由一个配送车队负责配送货物，选择最优的行车配送线路，使得客户需求得到满足，并且在特定的约束条件下，达到一些比如路程最大、费用最低和成本最小以及时间最少等目的。

自VRP问题被提出，国内外学者分别从不同角度，使用不同方法对其进行研究。在国外，1991年，Gendrean等人将禁忌搜索算法应用于VRP中[2]。1996年，J.Lawrence将遗传算法用于VRP研究中，并可有效求解带时间窗口的VRP问题[3]。Archetti等通过分别对车辆路径问题（VRP）和交付车辆路径问题进行实例研究，分别得出在有限车容量情况下和无限制车容量情况下的最优配置问题[4]。国内VRP研究起步较晚，刘浩等研究了随机需求VRP问题，在服务仅能路由失败一次和不允许部分服务的情况下，给出了两阶段模拟退火算法[5]。朱孟高等针对现有算法在多约束下车辆调度优化问题求解方面的不足，提出两阶段启发式算法，即采用集束式算法进行客户点的合并，从而降低了全局搜索范围[6]。张健同等通过具体数例分析了节约法得到的配送方案，针对出现的配送路径交叉的情况，结合扫描法给出了一种改进节约算法[7]。最后通过具体的算例用这两种算法进行了对比计算。本文通过C-W节约算法与Logware仿真进行计算，进行对比。

1 模型构建

研究物流配送模型下的车辆调度问题一般会有以下几点假设：

（1）假设所有配送的货物都可以进行混装。

（2）假设每个需求点的需求量已知。

（3）假设从配送中心到各个配送点以及各配送点之间的距离都已知。

（4）假设配送中心具有足够的货物量和车辆数。

物流配送车辆调度的目的是使总费用最小，就一般情况而言，也可以说是车辆的总运输吨公里数最小。即找到满足条件的最优行驶路线。车辆调度模型的配送路线，主要满足以下的约束条件：

（1）必须满足所有配送点的需求品种数和需求量。

（2）对每一辆配送车辆，都要求配送的量小于或者等于车辆的最大载重量，而且对每一辆车都有运输路程约束。

物流配送车辆调度问题应在严格的符合上述约束条件的基础上求解最优配送路线，以及选择车辆类型和车辆数。运用这样的配送方法，要求按量、按时地完成配送点的需求的配送任务，而且还必须保证运输总吨公里数最小。

xi：配送网络中的节点，xi在i≠0表示配送点，在i=0表示配送中心；

n：配送需求点数；

w：每辆车的最大载重量；

K：车辆总数；

qi：每个配送点的需求量；

s：每辆车的最大运行路程；

wk：每辆车的运载量；

nk：车辆k配送的配送点数目；

pk：车辆k所配送的需求量；

gkij：车辆k从配送点i到配送点j的配送总路程；

dij：任意两个配送节点之间的距离。

物流车辆调度模型如下：

目标函数：

约束条件：

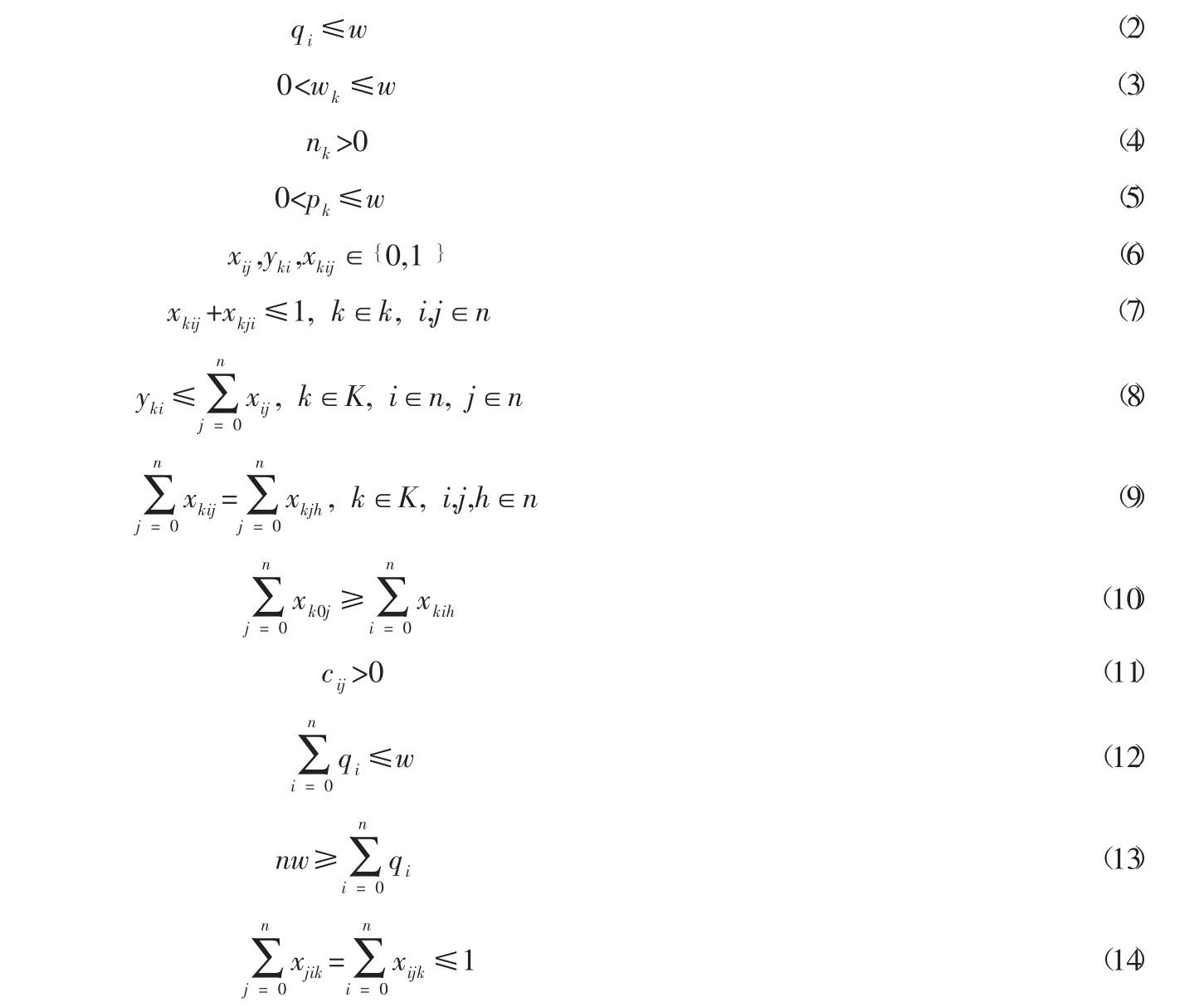
在上面的式子中，具体解释如下：

式（1）是目标函数，表示在车辆可以从i点到j点的情况下，总的运输距离最小。是配送车辆从配送中心到配送点及配送点之间的距离之和。式（2）表示任意每个配送点的需求量小于或者等于每辆车的最大载重量。式（3）表示任意每辆车的载重量大于0，但是要小于或者等于每辆车的最大载重量。式（4）表示任意一辆车配送的配送点的数目都要大于0。式（5）表示任意每辆车配送的需求点需求量要小于车辆的最大载重量。式（6）表示任意两个点之间的配送路线情况，即xij=0表示i点和j点没有配送路线，xij=1表示i点和j点有配送路线。车辆从一个配送点到另一个配送点之间的情况，即xkij=0表示车辆k不可以从配送需求点i到配送需求点j，xkij=1表示车辆k可以从配送需求的i到配送需求点j。车辆对配送点的服务情况，即yki=0表示车辆k不对配送需求的i服务，yki=1表示车辆k对配送需求点i服务。式（7）表示每条路径最多只能走一次。式（8）表示只有在某一配送车辆经过某一配送需求点，该辆车才能对该配送需求点进行服务。式（9）表示中间顶点的平衡，即对于某一配送需求点，其进入的配送路线与出去的配送线路相等。式（10）表示配送车辆数大于或等于配送的路径数。式（11）表示配送中心到任意一个配送需求点或者任意两个配送需求点之间的距离大于0。式（12）表示一条路径上的配送需求点的需求量要小于或者等于车辆的最大载重量。式（13）表示配送中心的货物总量要满足客户需求量。式（14）表示每一个配送点最多只能服务一次。

2 算法简介

2.1 C-W节约算法

节约法（the Clarke-Wright algorithm）是启发式算法中最常用的一种算法，是1964年由Clarke和Wright提出的，是根据配送中心的配送能力和物流配送中心到各配送需求点以及各配送需求点之间的距离，制定使总的车辆运输吨公里数（或者时间或者费用）最小的方案。

C-W节约算法的计算步骤如下[7]：

Step1：根据配送中心以及各配送需求点的坐标，运用欧式距离公式计算出配送中心至各配送需求点以及各配送需求点之间的距离，得到距离矩阵dist。

其中，v［i］,v［j］表示配送需求的i和j。v［i］·x和v［j］·y表示x和y点的横坐标。v［i］·x和v［j］·y表示x和y的纵坐标。dist［i］［j］表示i和j点的距离。i=0表示配送中心。

Step2：由距离矩阵计算出任意两个配送需求点的节约值，得出节约值矩阵savingvalue。

此时，设lij=lji，lij表示i到j的距离，i=0表示配送中心。

Step3：为了按照节约值的大小对配送需求点进行由大到小的排序,需要将节约值矩阵savingvalue转换为节约值表savingvaluetable。

Step4：从排好序的节约值表中取出第一项，而且判断是否要将其加入到当前的路径中。具体如图1所示：

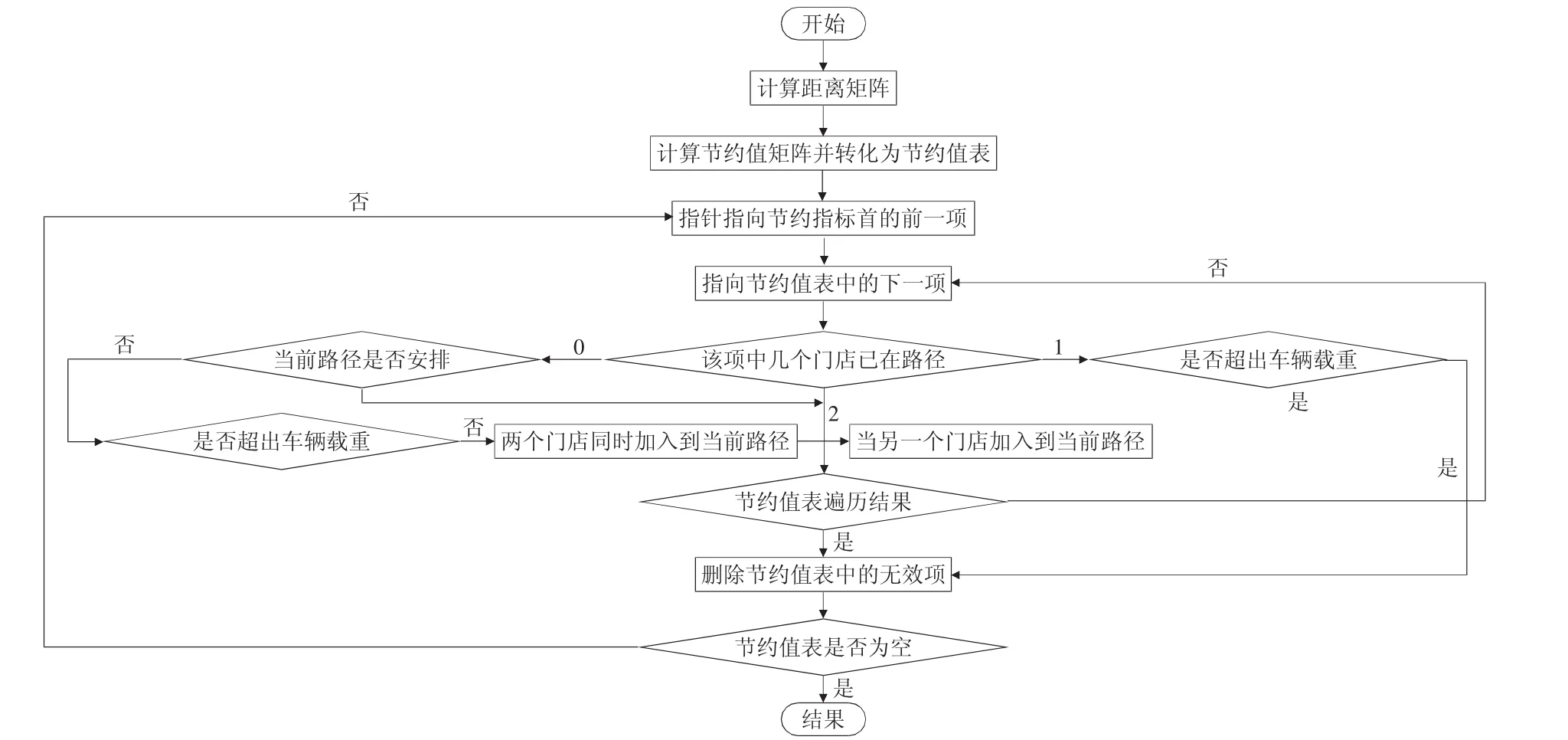
图1 节约法流程图

2.2 Logware软件概述

Logware是一组选定的软件程序，用于分析各种物流/供应链问题和案例研究。它包含以下模块：FORECAST：通过指数平滑法预测时间序列数据和时间序列分解方法；ROUTE：找到路网的最短路径；ROUTESEQ：找到线路上访问点的最佳顺序；ROUTER：多车型访问多个客户的路线选择；INPOL：基于EOQ的库存订购决策；COG：根据精确中心法找到单个设施的位置；MULTICOG：根据精确重心法找到选择设施的数量；PMED：根据P-median方法找到设施的数量；WARELOCA：根据分析研究仓库位置；LAYOUT：商品在仓库和其他设施的位置；MILES：使用经度或linear-grid坐标点计算两点之间的近似距离；TRANLP：解决交通的线性规划方法；LNPROG：解决一般线性规划问题的单纯形法；MIPROG：解决混合整数线性规划问题的分支界限法；MULREG：通过逐步回归和相关分析发现线性回归方程的程序；SCSIM：通过五阶层的供应渠道模拟产品的流动。

其中本文运用ROUTER模块；ROUTER模块是一个由私人控制车队来确定最佳路线和时间表的软件程序。主要有以下输入：坐标点、放缩比例因子、站点时间限制、道路限制、速度地带、距离、打断时间、时间窗口、取货交货、取货政策、车辆、路线费用、线路中的障碍物等。

3 案例分析

设有10个医院，其中0表示医药配送中心。配送中心位于坐标原点，车辆最大载重为400t。下面是各门店的坐标以及需求量（见表1）。找到最优配送路线（见表2）。

表1 门店坐标及需求量

表2 C-W配送路线

（1）利用C-W节约法计算

可以看到共有4条配送路线：

①0-6-2-5-0运输量282t，运输里程为29.4+24.1+36.1+53.2=142.8，节约里程为47.3+59.1=106.6。

②0-1-8-3-0运输量为194t，运输里程为46.0+15.7+17.5+20.0=99.2，节约里程为62.3+34.5=96.8。

③0-9-10-7-0运输量为25t，运输里程为33.2+21.6+14.2+20.1=89.1，节约里程为33.5+27.8=61。

④0-4运输量为179t，运输里程为8.5。

（2） 配送路线如图2（a） 所示：Logware配送路线

可以看到共有3条配送路线，其配送路线图如图2（b）所示：

①0-5-2-6-0运输量为282t，运输里程为53.2+36.1+24.1+29.4=142.8，节约里程为47.3+59.1=106.6。

②0-1-8-3-7-0运输量为289t，运输里程为46.0+15.7+17.5+10.2+2.1=109.5，节约里程为62.3+34.5+30.0=126.8。

③0-9-10-4运输量为369t，运输里程为33.2+21.6+17.0+8.5=80.3，节约里程为33.5+13.4=46.9。

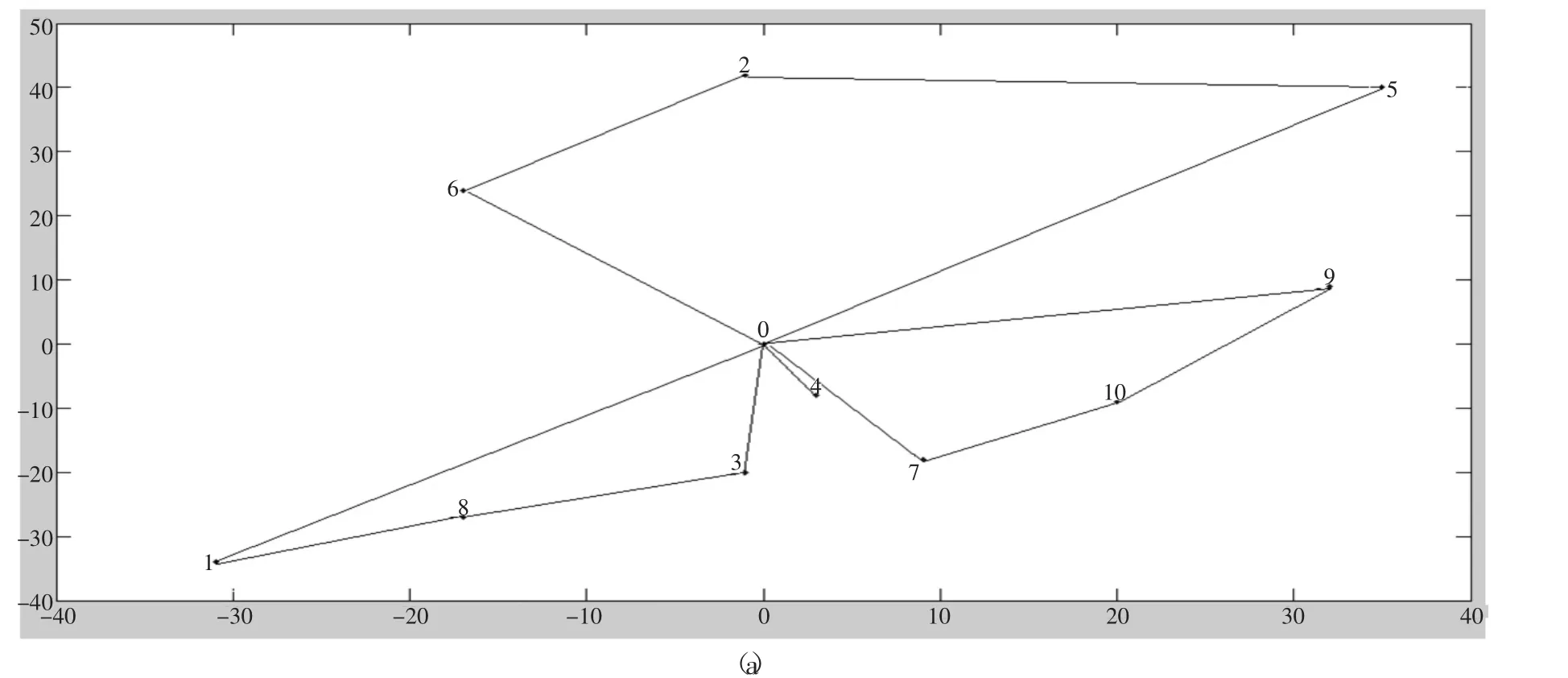
图2 配送路线图

其中，C-W节约法的MATLAB程序计算的总运输里程为339.6，节约里程为264.4。Logware软件计算的总的运输里程为332.6，节约里程为280.3。运输里程相差7。

由上面的两个例子可以看出，Logware软件比C-W节约值的MATLAB程序实现的路径更优，这是因为运用C-W节约法过分注重节约的里程而没有考虑时间因素，并且没有考虑运输过程中花费的费用，而且C-W节约法不能对客户的需求进行灵活处理。

4 结论

本文对VRP问题进行了描述，建立了一般物流配送的VRP模型，然后对物流配送的VRP问题在一定的前提和假设条件下进行了模型分析与建立。本文的主要假设有：假设所有配送的货物都可以进行混装，假设每个需求点的需求量已知，假设从配送中心到各个配送点以及各配送点之间的距离都已知，假设配送中心具有足够的货物量和车辆数。根据假设条件建立了目标函数和约束条件。通过对两种方法的比较，发现Logware软件更加优化一些。这是因为运用C-W节约法过分注重节约的里程而没有考虑时间因素，而且C-W节约法不能对客户的需求进行灵活处理，而Logware可以处理这些问题。

[1]Dantzig G B,Ramser J H.The truck dispatching problem[J].Management science,1959,6(1):80-91.

[2] Gendrean M,Hertz A,Laporte G.A tabu search heuristic for the vehicle routing problem[M].Management Sci,1994,40:1276-1290.

[3] Lawrenee S.Mohammad.A Parametric experimentation with a genetic algorithmic configuration for solving the vehicle routing problem[C]//Proceedings-Annual Meeting of the Decision sciences Institute.Decis Scil Inst,1996:488-490.

[4] Archetti C,Feillet D,Gendreau M,et al.Complexity of the VRP and SDVRP[J].Transportation Research Part C:Emerging Technologies,2011,19(5):741-750.

[5] 刘浩，钱小燕，王荣.随机需求VRP的一个算法[J].南京工业大学学报，2004,26(5):9-11.

[6] 朱孟高，米娜.城市配送车辆路径优化集束式算法的客户点归并策略[J].数学的实践与认识，2012(11):47-51.

[7] 张健同，冯子炎.求解车辆路径问题的改进C-W节约算法[C]//第十届中国不确定系统年会、第十四届中国青年信息与管理学者大会论文集，2012.

[8] G.Clkare,J.w.wright.Scheduling of Vehieles from a Central Depot to a Number of Delivery Points[J].Oeration Researeh,1963,11:568-581.