K-means聚类蚁群优化算法求解大型TSP问题
2018-03-16郑旭峰周健勇ZHENGXufengZHOUJianyong
郑旭峰,周健勇 ZHENG Xufeng,ZHOU Jianyong
(上海理工大学 管理学院,上海 200093)
0 引 言
旅行商问题,即TSP问题(Travelling Salesman Problem)是经典组合优化问题,其目标是求出商人有且仅有一次经过N个城市并最后回到原点的最短路径。当问题规模N较小时,枚举法是求解TSP的简单方法。随着N的增大,该方法显然在时间和空间上都是不可行的。20世纪90年代,意大利学者Dorigo,Maniezzo等人最先提出蚁群算法(Ant Colony Algorithm),并将这种新的启发式算法应用于TSP、资源二次分配问题等经典优化问题,得到了较好的效果[1]。
物流配送是TSP问题在物流领域的描述,是现代企业生产过程中的重要环节,其配送速度是决定了独立的物流团队以此来保证配送的服务质量。随着当今电子商务平台火热发展,人们越来越倾向在网上购物,物流公司的经营范围日益扩大,配送对象也成倍增加,从而对配送路径的选择产生时间与空间的高复杂性问题。为了保证配送速度与配送成本,大规模的物流配送路径优化问题成为重要研究课题。现实生活中物流配送对象常常具有地域空间特性:如A地区的若干个小区距离相近,且都由同一家物流公司配送,B地区同样有若干小区,也有配送任务,这类物流配送问题带有明显的聚类特性。
文献[2]针对传统蚁群算法处理TSP问题时易于出现早熟停滞现象,引入局部信息激素及最优最差路径信息激素更新策略,有效抑制早熟停滞,加快算法收敛速度。戚玉涛等[3]通过自适应规约免疫算法,采用多级归约来求解大规模TSP问题。文献[4]将遗传算法的复制 、交叉和变异等遗传算子引入蚁群算法,建立了带约束条件的物流配送数学模型,可以有效而快速地求得问题的最优解或近似最优解。袁亚博等[5]在求解最短路径问题上对经典蚁群算法提出三方面改进,首先加入方向引导,提高搜索速度,随后根据信息素重新分配更新局部浓度,最后引入动态因子提高算法自适应性。文献[6]以碳排放成本为目标函数,在混沌系统及模拟退火机制上引入基本蚁群算法,研究了低碳物流配送路径优化问题。
尽管以上许多改进的蚁群算法成功应用于多个组合优化问题,但是仍存在一些不足,这在处理大规模问题时尤其明显,如计算时间较长,误差率增大等。本文针对这类带聚类特性的TSP问题,提出K-means聚类蚁群算法(K-means Clustering Ant Colony Algorithm)。该算法首先对数据集中的城市采用K-means算法进行聚类分析,找出满足最优紧密度的聚类个数,随后将大规模城市集合分成若干个小规模城市集合,分别运用传统蚁群算法对其求出最短路径,最后将这些已求解的小规模城市集中的出入度城市通过设定的规则连接起来,从而完成对原始问题的求解。本文结合K-means聚类和蚁群算法提出解决大规模城市集的聚类蚁群算法—K-means蚁群算法(KMACA),并与蚁群聚类蚁群算法(ACACA)和传统的蚁群算法(ACA)进行比较。
1 算法原理及实现
1.1 KMACA聚类原理
对于求解大规模的TSP问题,KMACA算法第一步需要确定对大规模城市集如何聚类。经典的K-means算法用于聚类时,若结果类是密集的,且类与类界限较明显时,效果较好。该算法对于大规模数据集是相对可伸缩和高效率的[7-8],因此用K-means算法来对大规模TSP问题聚类是合理的。
但作为一种无监督的知识发现算法,K-means聚类算法缺点之一是需要事先确定聚类的个数K,因此在对数据分布一无所知的情况下,有必要对不同聚类K做有效性分析,类内的凝聚度(Cohesion)和类间的分离度(Separation)通常作为聚类效果的主要特性,好的聚类结果应具有较小的类间凝聚度,同时又具有较大的类间分离度[9]。轮廓系数指标结合了凝聚度与分离度,具体公式如下:

假设样本di聚集到A类,ai代表样本di与A簇其他样本的平均距离,令D( di, )C 为样本di与C簇平均距离,则(di, C )。对某次聚类来说,n为城市数,K为聚类数,Sk反应了总体平均轮廓系数。Sk取值介于-1与1之间,值越大,聚类效果越好,本文选取K从2到10依次迭代,选取Si最大值时的K作为聚类个数。101个城市规模轮廓系数迭代效果与K-means聚类效果分别如图1、图2所示:

图1 轮廓系数图
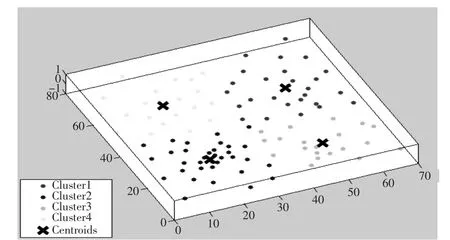
图2 大规模TSP问题的K-means算法聚类效果图
从图1可以发现以下特征:
(1)整个大规模数据集可以人为聚成K类,设每类包含的个数为nk,则有为总体城市规模个数,每个类i中都存在一个聚类中心点ci。
(2)对于某一特定类,我们可以用蚁群算法求解出最短路径,并预留出入度城市。
(3)为了将最优子结构连接起来,设置一定规则连接出入度城市。
(4)当式(1)中的K>3时,需要对所分的类进行最短路径的连接,此时可以对式(1)聚类中心点C1,C2,…,Ck求最短路径,考虑到K值不会太大,故用传统的TSP算法可以求解。
1.2 KMACA类内连接顺序
1.1 节完成了对大规模TSP问题的聚类,为了求解原始问题,下一步需要找到每个类中的出入度城市来完成与邻类的相连。
类的出入度城市选择对类内的城市连接有很大的影响。本文优先考虑类内的最短路径,与传统的TSP问题不同的是,该最短路径不需要回到起始点,即该路径是开放的。开放的最短路径在传统的TSP最短路径上需再进一步,对于类中的点集A,不妨设(m≠n,m,n∈A)为m与n点的距离,设封闭的最短总路径为D,类的出入度城市随机,则开放的类内最短路径为minDmin-,若还存在更短路径DNEW,连接首尾,因为,因此DNEW+<Dmin,出现矛盾,则Dmin-就是类内最短开放路径长度,且出入度城市为m和n。
1.3 KMACA类间连接顺序
当聚类个数超过3时,不妨设各类的聚类中心点为C1,C2,…,Ck,为使TSP问题的解最优,类与类所连接的边之和应最小。因聚类数K较小,故用处理小规模的TSP问题算法对C1,C2,…,Ck进行排列连接即可。
1.4 KMACA类的出入度连接
在以类内最短连接距离优先的前提下,每类i自然会留下两个开放点,不妨设入度城市为,出度城市为,对于第一个类1,其出度城市有两个选择,与类1相连的类2,其入度城市有也有两个选择,依次类推,K类中类的出入度总的连接方式为2k,迭代即可确定最短的连接方式。考虑到K值较小,这种指数型增长仍可接受。整个算法流程如图3所示:
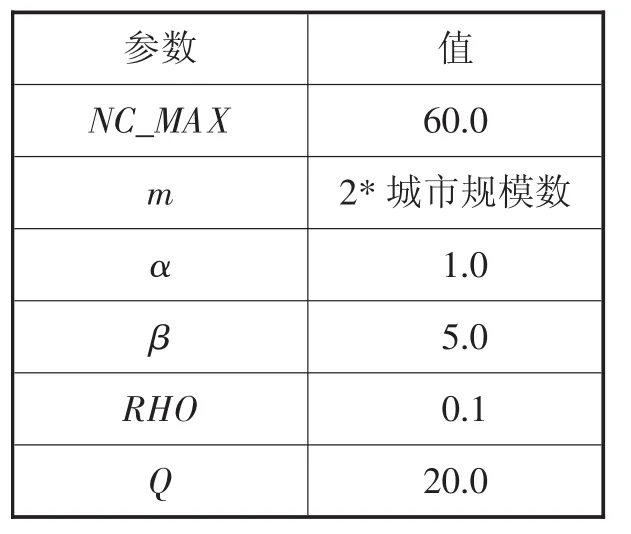
表1 蚁群算法参数设置表
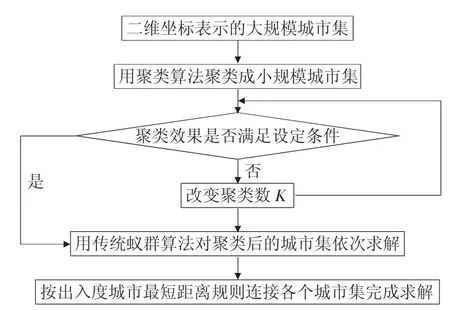
图3KMACA算法流程图
2 实验仿真及分析
2.1 实验仿真
实验选用TSP标准数据集中的5个实例eil101、pr299、d493、rat575、rat783,通过传统蚁群ACA算法、KMACA算法与ACACA算法进行对比实验,运行MATLAB R2010a,在内存为4 GB,Intel corei7-3770处理器的PC机上进行模拟仿真。算法参数设置如表1所示:
NC_MAX为最大迭代次数;α表示信息素重要程度,增大α有利于后面的蚂蚁吸取前面的经验,但取值过大容易陷入局部最优;β表示启发式因子重要程度,增大β有利于解的多样化,探究到更优的路径,过大会使搜寻时间变长;RHO为信息素蒸发系数,对于迭代次数比较大的,敏感程度较小;Q为常系数,ACACA算法运用蚁群聚类时,设定迭代次数达到20 000次聚类即结束。数值优化设定参考[10]。本次试验按照以上参数对前4种规模的TSP问题进行了20次,rat783运行了5次,平均实验结果如表2所示:
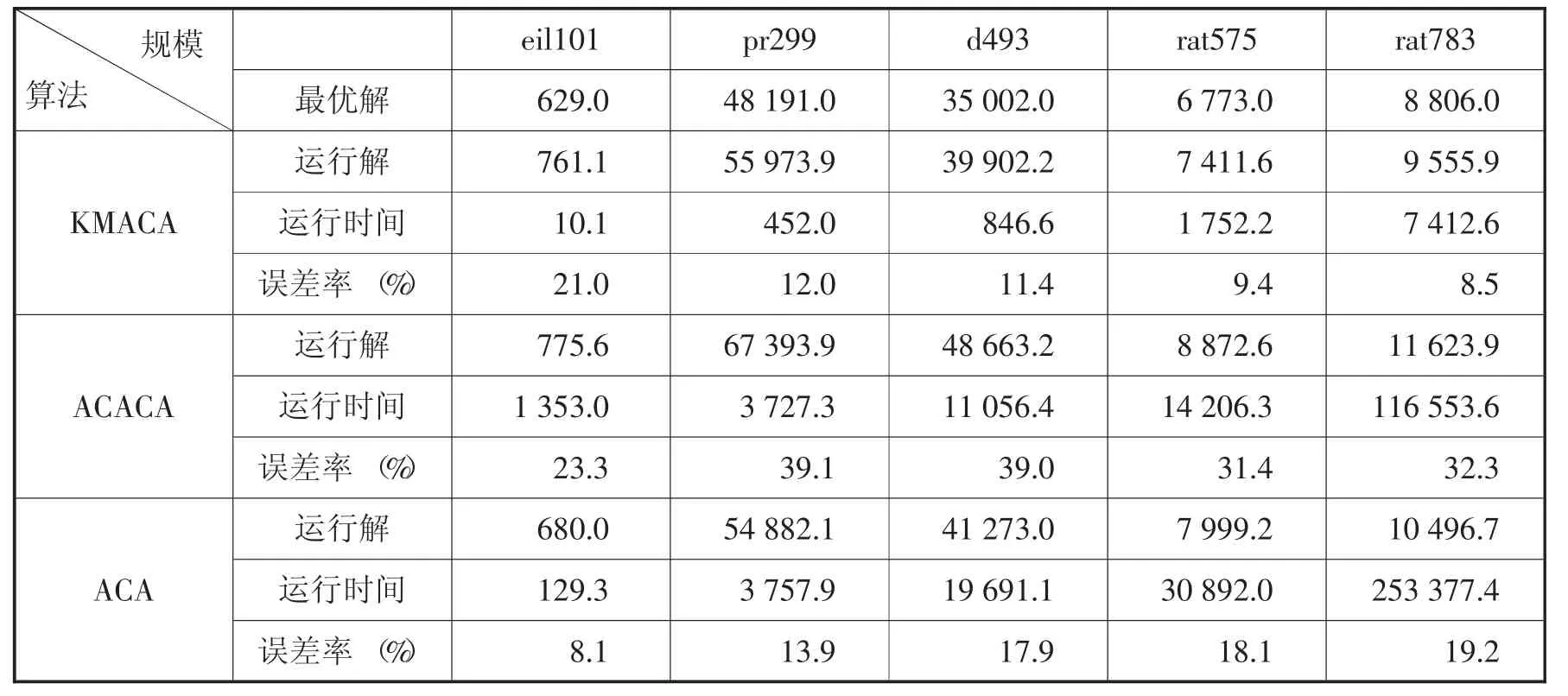
表2 5种规模下ACA/KMACA/ACACA效果对比
2.2 结果分析
根据表2得出的实验数据,分别从算法运行时间与误差率两个方面分析比较3种算法的效果。如图4、图5所示:
从运行时间上看,3种算法运行时间均和城市规模呈正相关,跟最短路径的长度没有必然关系。其中对整个规模直接求解的ACA算法对数化后的运行时间与城市规模呈明显的线性关系,如图6所示:
因此用传统的ACA算法运行时间T与规模N的关系为:

KMACA算法运行时间由聚类时间、各个子类的最短路径求解时间和连接子类时间组成。仿真实验中聚类与连接时间在总时间中的比例可忽略不计。因此其运行时间主要与聚类数K相关,同一规模下,聚类数越多,其速度越快,但聚类数过多会影响增大结果误差,具体K参考1.1节的最大轮廓系数。
ACACA算法运行时间组成与KMCAC类似,不同的是蚁群聚类算法对数据的要求较少,无需事先确定聚类数,适用范围较广,但产生的问题是聚类时间占比很大,超过了各个子类最短路径求解时间之和。效果上看,在前两个eil101、pr299数据集中,ACA算法运行时间是KMACA时间10倍左右,在后3个数据集中,这个比值达到20倍以上。在ACA算法与ACACA算法对比中,除了第一个数据集以外,ACA运行时间是ACACA的2倍。由于ACACA聚类中以迭代次数为终止条件,因此在小规模数据集中,后面的迭代对聚类效果没有改进,反而增加了求解时间。因此在运行时间对比上,KMACA算法比另外两个算法速度快得多。
从误差率方面看,ACA算法随着规模增大而缓慢增加,KMACA算法在eil101规模上误差率较大,随后缓慢下降,ACACA算法的误差率明显高于另外两种算法。由于ACACA与KMACA原理实现的唯一区别是聚类方式,因此推断ACACA中的蚁群聚类效果不好,不适合对二维空间上的点进行聚类。对KMACA算法在eil101中的高误差率分析发现,eil101数据集的最短距离基数过小,仅为629,导致聚类间相连的距离相对过大,为134.5,因此聚类对小规模的数据集影响过大,分类后的总体距离效果不佳,这也从侧面反映了KMACA算法不是处理小规模问题的优秀算法。

图4 算法运行时间对比图
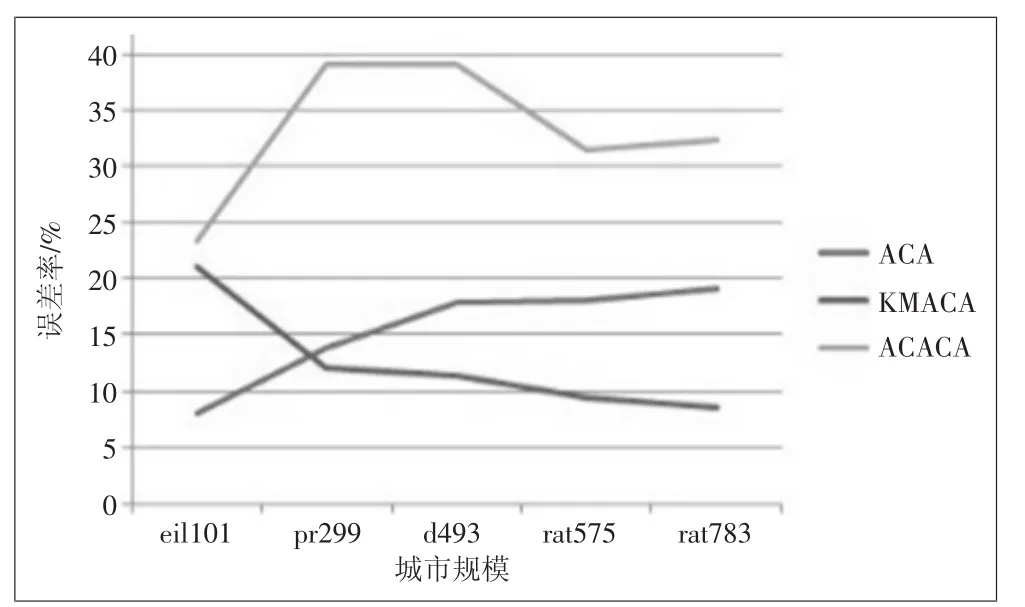
图5 算法误差率对比图
3 结束语
本文针对传统ACA算法处理大规模TSP问题出现的不足,结合物流配送过程中目的地聚集特征,提出了K-means聚类蚁群算法—KMACA,并与ACACA算法和ACA算法分别从运行时间与误差率上进行比较。根据结果分析,K-means蚁群算法在运行时间上远好于ACA与ACACA算法,在结果误差率上,K-means算法小于ACA算法,而ACACA算法则由于蚁群聚类效果不佳导致误差率很高。总体来讲,K-means算法对比传统的ACA算法在两个方面均有提升,运行时间上尤其明显。现实生活中,尽管能确定适当的聚类数K,但是该数量聚类下紧密程度对实验值与真实值误差的影响事先难以确定,故其实用性有一定的限制;另外当前优秀的物流配送常常带有配送时间的限制,需要考虑时间窗因素,本文未把其考虑在内,以后将进一步研究。
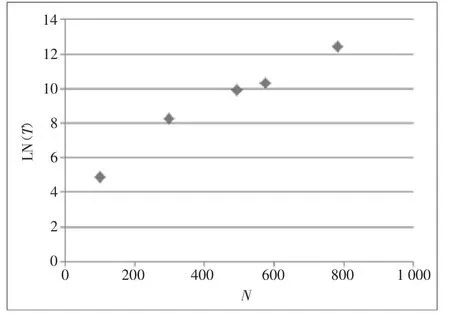
图6 规模运行时间关系图
[1] Tzle T,Dorigo M.ACO algorithms for the quadratic assignment problem[M].McGraw-Hill Ltd.UK,1999.
[2] 张军英,敖磊,贾江涛.求解TSP问题的改进蚁群算法[J].西安电子科技大学学报,2005,32(5):681-685.
[3] 戚玉涛,刘芳,焦李成.求解大规模TSP问题的自适应归约免疫算法[J].软件学报,2008,19(6):1265-1273.
[4] 张维泽,林剑波,吴洪森.基于改进蚁群算法的物流配送路径优化[J].浙江大学学报(工学版),2008,42(4):574-578.
[5] 袁亚博,刘羿,吴斌.改进蚁群算法求解最短路径问题[J].计算机工程与应用,2016,52(6):8-12.
[6] 张立毅,王迎,费腾.混沌扰动模拟退火蚁群算法低碳物流路径优化[J].计算机工程与应用,2017,53(1):63-68.
[7] 孙士保,秦克云.改进的k-平均聚类算法研究[J].计算机工程,2007,33(13):200-201.
[8] 孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008(1):48-61.
[9] 朱连江,马炳先,赵学泉.基于轮廓系数的聚类有效性分析[J].计算机应用,2010(s2):139-141.
[10]柳长源,毕晓君,韦琦.基于蚁群算法求解TSP问题的参数优化与仿真[J].信息技术,2009(4):129-131.
