点到直线的距离公式及其在基坑监测中的应用

戴水财，戴戈晖

(1.中南大学地球科学与信息物理学院，湖南 长沙 410083； 2.湖南师范大学附属中学，湖南 长沙 410006)

1 点到直线的距离公式

(A2+B2)S2=(A2+B2)[(x-x0)2+(y-y0)2]=A2(x-x0)2+B2(y-y0)2+A2(y-y0)2+B2(x-x0)2

=[A(x-x0)+B(y-y0)]2+[A(y-y0)-B(x-x0)]2

≥[A(x-x0)+B(y-y0)]2=(Ax0+By0+C)2(∵Ax+By+C=0)

(1)

(2)

2 实际工作中直线方程的表达方式

实际工作中，直线l往往用经过两点的坐标方式表达。如直线经过P1(x1，y1)和P2(x2，y2)。则直线l的表达方程为：

(y2-y1)x-(x2-x1)y+y1x2-y2x1=0

(3)

其中：A=y2-y1B=x1-x2C=y1x2-y2x1

(4)

(5)

3 点与直线位置关系的判断

判断点P0(x0，y0)与直线l：Ax+By+C=0的位置关系，就是要确定点P0(x0，y0)在直线l的左边还是右边(或者是上边还是下边)。

过点P0(x0，y0) 作一条水平直线y=y0，与直线l：Ax+By+C=0相交于P′(x′，y0)，如图1所示，则：

(6)

当x′≥x0时，点P0(x0，y0)与直线l的左侧(或下边)；

当x′≤x0时，点P0(x0，y0)与直线l的右侧(或上边)。

图1 点与直线的位置关系

4 点到直线的距离的工程应用

在现实生活中，经常需要间接求解点到某一条特定直线的距离。如城市基础设施建设中，经常需要开挖建筑基坑。开挖基坑时需要在基坑顶部的围护结构上布设测量点，监测支护结构的水平位移变化，而位移变化的重要方向就是基坑边的垂直方向，因此，需要间接求解监测点位到基坑边垂直方向的距离。如果开始确定一个初始基准值，就可以连续测量出测点位到基坑边垂直方向的变化量，这个变化量对于判断基坑是否安全非常重要。需要说明的是，工程坐标系的X/Y轴和数学坐标系的X/Y轴正好相反。因此，计算时需要把工程坐标系的X坐标和Y坐标交换，代入上述计算公式。

以长沙市地铁3号线某车站基坑为例。该车站基坑水平位移监测的工程坐标经过处理后的原始测量数据见表1，地铁车站基坑部分水平位移测点位置平面图见图2。该基坑四个端点分别为1号、5号、7号和11号，四条边分别为1-5、5-7、7-11和11-1。基坑边1-5布设有2号、3号和4号监测点；基坑边5-7布设有6号监测点；基坑边7-11布设有8号、9号和10号监测点。基坑四条边的直线方程系数计算结果见表2。监测点到基坑边的垂直距离计算结果见表3，这个计算结果与图2中CAD作图得出的结果一致。

基坑测量数据 表1

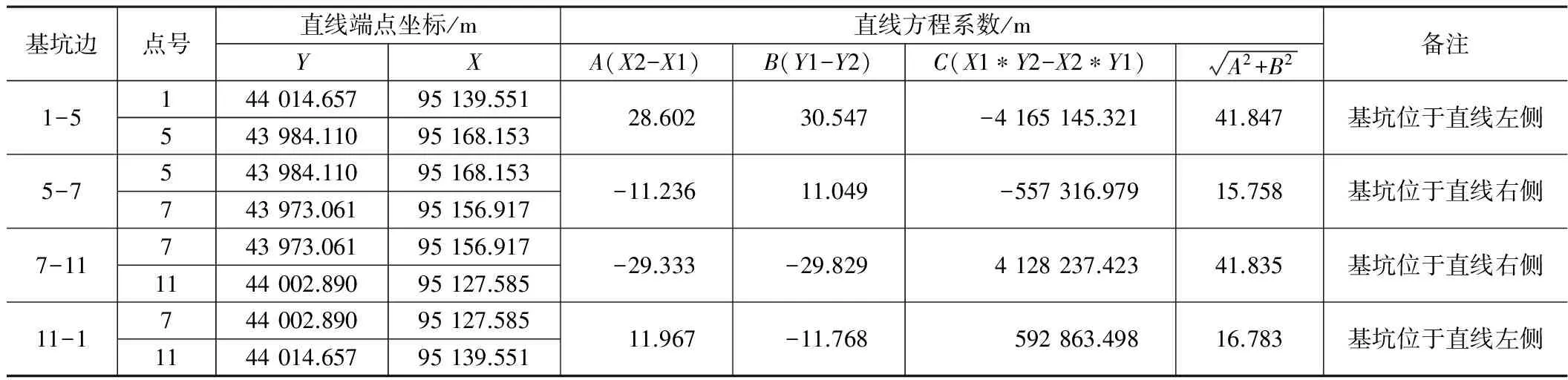
基坑边直线方程系数 表2

测量点到基坑边的垂直距离 表3

图2 地铁车站基坑水平位移测点位置平面图

5 结 语

本文介绍了点P0(x0，y0)到直线l：Ax+By+C=0的距离公式的推导，并结合工程实例，对基坑测量监测点位对于基坑边垂直方向变化的大小和方向进行了分析和计算，测量数据可以在电子计算表格中自动编程实现，还可以用编程语言编辑程序更好实现。在此基础上，可以进一步对一个时期的测量数据进行变形分析，对于监控基坑的安全有着重要的意义。

[1] 张景中. 湖南新人教A版高中数学[M]. 长沙：湖南人民出版社，2016.

[2] 李桂珍，王全牢. 点到直线距离公式的多种推导方法[J]. 集宁师专学报，2000(4)：93～94.

[3] 高俊强，严伟标. 工程监测技术及其应用[M]. 北京：国防工业出版社，2005.

[4] 翟翊，赵夫来，郝向阳. 现代测量学[M]. 北京：测绘出版社，2016.

[5] 张正禄. 工程测量学[M]. 武汉：武汉大学出版社，2013.

[6] 卢珍凤. 点到直线距离公式的引伸及应用[J]. 高职教育，2011(4)：159.

[7] 刘古胜，邓严林. 点到直线的距离公式的推证[J]. 沙洋师范高等专科学校学报，2005(5)：26～27.

[8] 李凌. 点到直线距离公式的几种初等数学证法探讨 [J]. 科教文汇(中旬刊)，2008(3)：88.