银川地区临床用血需求预测数学模型的建立与应用
2018-03-15李艳丽张伟李平樊荣韩文丽李双琴李娟
李艳丽 张伟 李平 樊荣 韩文丽 李双琴 李娟
(宁夏血液中心 宁夏 银川 750021)
自愿无偿献血作为临床用血的主要来源,采供血机构在保障血液的采集、临床供需平衡以及血液质量中发挥着至关重要的作用[1]。随着经济社会的快速发展,银川地区临床用血需求急剧增长,以每年10~12%的速度递增,血液供需矛盾日趋凸显,血源组织和血液采集工作面临的压力和挑战与日俱增。为有效应对临床用血现状,在保证满足临床用血量的同时,减少和避免因过量采集而导致过期报废等血液资源的浪费,作者现对银川地区临床供血量进行分析,并预测未来的用血需求,为制定银川地区临床供血量提供科学、合理的数据支持。
1.材料与方法
1.1 分析资料来源
以宁夏血液中心2005—2016年临床供应红细胞量(200ml全血为1U)作为统计分析数据来源,统计数据以宁夏血液中心穿越信息管理系统为准。
1.2 方法
考虑临床用血量可能具有一定的趋势、周期性等特点,选择兼顾趋势性、周期性及循环性的ARIMA模型对数据进行拟合,并筛选最佳模型,同时用2016年7月—2017年6月的数据对模型进行验证,并用于预测未来一段时间银川地区的临床用血量。
1.3 统计分析
采用SPSS19.0软件进行数据的统计分析,P<0.05有统计学意义。
2.结果
2.1 基本情况
银川地区2005—2014年临床用血量逐年增加,2015年略有下降。与2005年相比,2010年临床用血量平均增长速度达19%,其余年份的平均增长速度超过12%,详见表1。
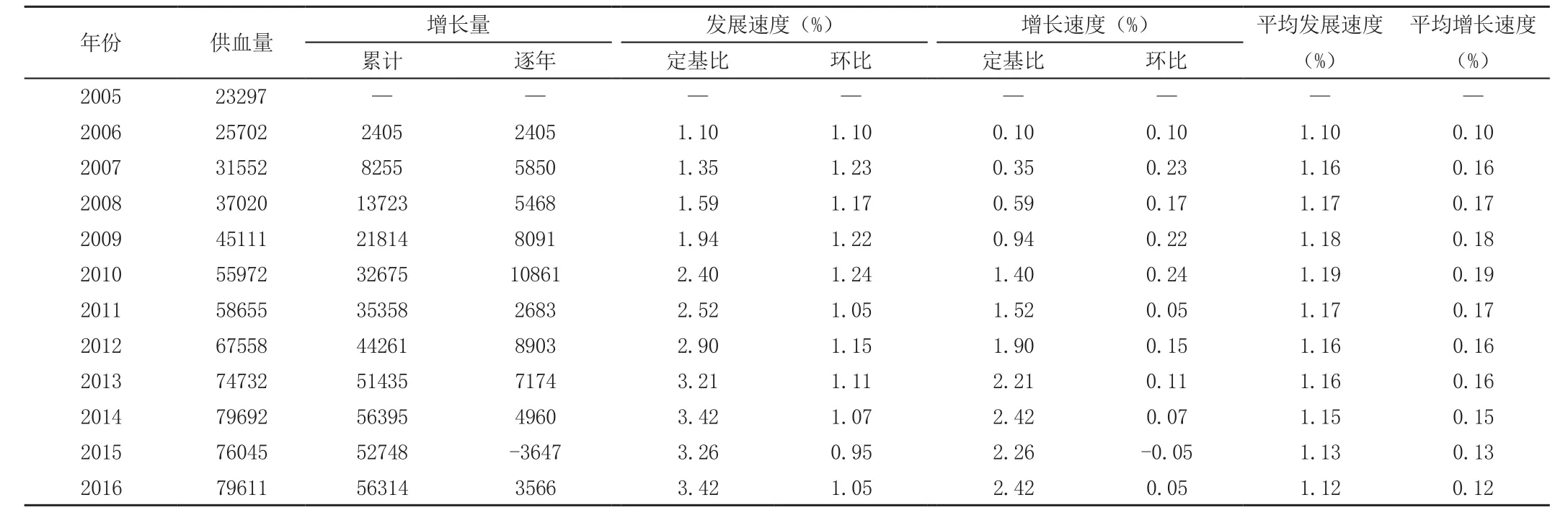
表1 银川地区2005—2016年临床用血量
2.2 数学模型的建立
用2005—2016年的月度临床用血量进行建模。月度数据呈上升趋势,且呈现一定的周期性。对数据进行一阶差分和一阶季节性差分后,数据呈平稳序列。通过ARIMA模型,从低阶到高阶逐个对p、q和P、Q的取值进行尝试,结合BIC准则选取BIC值最小的模型ARIMA(0,1,1)(0,1,1)12为最佳模型,平稳R方为0.795。序列的Ljung-Box Q检验显示差异无显著性(统计量Q=15.122,P=0.516),表明残差序列为白噪声,进一步证实了所选模型是恰当的。模型的表达式为(1-L)(1-L4)Yt=(1+0.85L)(1+0.858L12)εt。ARIMA模型参数见表2。图1为2005—2016年月度数据的残差图,图2为2005—2016年月度数据的拟合曲线。
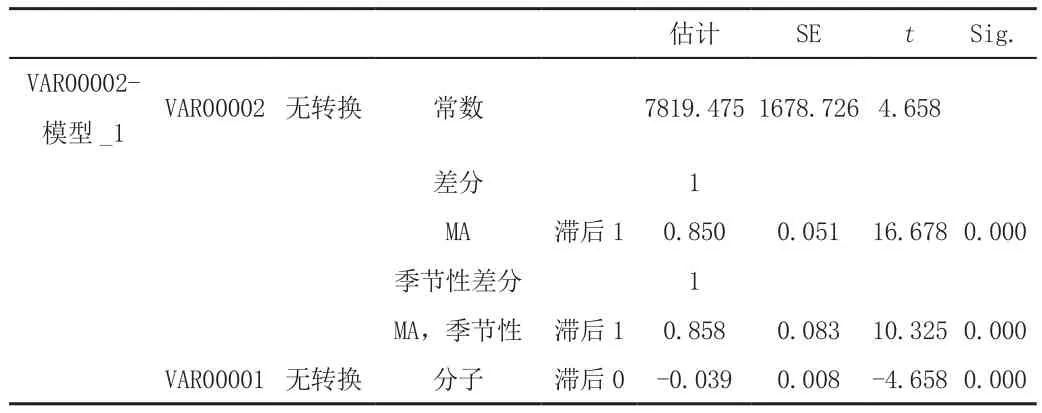
表2 ARIMA 模型参数
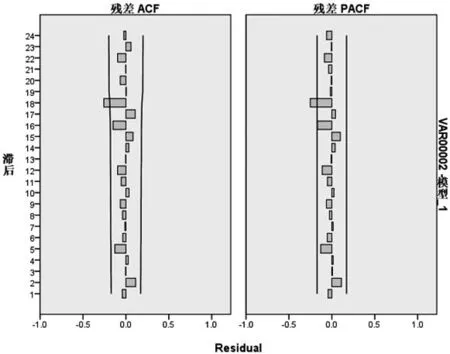
图1 2005—2016年月度数据的残差图

图2 2005—2016年月度数据的拟合曲线
2.3 数学模型的验证
用2016年7月—2017年6月的数据进行验证,除2017年2月的相对误差高于10%以外,其余月份的相对误差都低于10%,说明模型的选择是正确的,可将其用于临床用血需求的预测。表3为月度模型的实际值与预测值。

表3 月度模型的实际值与预测值
3.讨论
血液作为一种特殊的医疗资源目前还不能实现体外制造[3],在临床救治中发挥着重要的作用。自愿无偿献血作为临床用血的主要来源,采供血机构在保障血液的采集、临床供需平衡以及血液质量中发挥着至关重要的作用。1998年《中华人民共和国献血法》颁布,对无偿献血工作发挥了极大的推动作用。银川地区居民回族占三分之一,受民族传统习俗,回族居民献血意识比较欠缺,人口献血率偏低,在一定程度上制约了临床用血量的储备。
血液资源需求预测是血液管理的重要环节,既可以有效的满足临床用血需求,同时又可避免过量采集而引发的血液资源浪费。所以采供血机构建立临床用血需求量数学模型来预测临床血液需求量,并在此基础上制定招募采集计划,合理安排团体献血,使经验性采血逐步转变成科学性、预见性采血[4],保持血液采集量和需求量的平衡是很有必要的。
时间序列预测方法是以惯性原理推测其未来的状态,常用的有指数平滑法,自回归求和移动平均模型(autoregressive integrated moving average model,ARIMA)[5]。ARIMA由Box和Jenkine于20世纪70年代初提出的著名时间序列预测方法[6]。ARIMA模型是目前较通用的时间序列预测模型之一,综合考虑了序列的趋势变化、周期变化及随机干扰,并借助模型参数进行了量化表达[7,8]。
银川地区2005—2016年月度临床用血量不仅含有时间趋势成分外,还混有季节性成分。如果只考虑单一的因素建立模型就不能准确的对其进行预测。因此,ARIMA乘积季节性模型非常适合对具有时间趋势,还混有季节性成分的数据进行预测[9]。2015年临床用血量有所回落,对预测的影响相对较大,分析其原因因为一段时间内血液供应紧张。在每年的2月,临床用血量处于低峰期(春节前后手术量少),10~11月处于用血的高峰期(产妇、农闲时手术高峰期)。考虑数据可能存在离群值,所以对离群值进行了检测,发现5个离群值,未参与模型的建立。2017年2月临床用血量受春节刚过的影响,实际供血量可能也属于离群值,所以致使预测值和真实值的相对误差高于10%。本研究证实了ARIMA模型在银川地区临床用血量的预测方面起了一定的作用,但也应该注意到,受诸多因素的影响,所建立的模型不是一成不变的,它较适合进行短期的预测,同时需要不断加入新的实际数据,以不断拟合更能反映实际情况的预测模型,才能达到预测的效果[6]。
[1]南京英.宣传形式决定无偿献血发展[J].世界最新医学信息文摘,2017,17(77):151.
[2]柳芳梅,梁社玲,段彩红,etal.宁夏血液中心2011-2015年临床供血调查及分析[J].中国输血杂志,2017,30(1):63-64.
[3]罗志红.2004-2008年湖南省临床用血情况和未来用血变化趋势分析[D];中南大学,2009.
[4]佘宇奇,李登清,邱明,等.2006—2012年长沙地区用血情况分析及趋势预测[J].中国输血杂志,2013,26(5):466-468.
[5]薛芳静,黄灏,许碧云,等.时间序列数据中的干预分析模型及SAS实现[J].中国卫生统计,2017,34(3):509-514.
[6]彭志行,陶红,贾成梅,等.时间序列分析在麻疹疫情预测预警中的应用研究[J].中国卫生统计,2010,27(5):459-463.
[7]王玉明.时间序列分析在甘肃省呼吸道传染病发病率预测中的应用研究[D];兰州大学,2009.
[8]温亮,张秀山,李承毅,等.季节分解法和ARIMA法预测乌鲁木齐市肺结核发病趋势效果分析[J].军事医学,2017,41(4):287-290.
[9]王超,丁勇,陆群,等.ARIMA乘积季节模型在我国甲肝发病预测中的应用[J].南京医科大学学报(自然科学版),2014,34(01):75-79.
