认知失调视角下网络舆论演化模式与对策研究
2018-03-14何建佳刘举胜王祥兵
何建佳 刘举胜 王祥兵
(1.上海理工大学 管理学院,上海 200093;2.贵州工程应用技术学院经济与管理学院,贵州 毕节 551700)
近年来,随着认知盈余的出现以及互联网技术的迅猛发展,以互联网为代表的数字技术正在加速与经济社会各领域深度融合,成为促进我国消费升级、经济社会转型、构建国家新优势的重要推动力。2017年7月,中国互联网络信息中心(CNNIC)发布了第40次中国互联网络发展状况统计报告,报告显示截至2017年6月,中国手机网民规模达7.24亿,较2016年年底增加2 830万人,网民中使用手机上网人群占比由2016年底的95.1%提升至96.3%[1]。在数字化时代背景下,一些受过教育,并拥有自由支配时间的网民开始在自我小型圈层中,以手机移动端为载体,微博、微信为平台进行发声与评议,潜在地参与社会公共活动,源源不断为社会输出新的内容,制造新的话题。在新的舆论形势下,如何合理引导网络舆论发展,构建和谐健康网络舆论环境,对促进社会共识涌现,化解网络舆情危机具有重要的理论与现实意义[2-4]。
舆论作为一种主观的,相对自由的、开放的思维结晶在个体之间可以进行广泛传播与演化。目前,舆论的演化主要集中于两种模式:一是自下而上的舆论演化模式,这种模式将个体看作微观粒子,个体之间观点的交互近似看作粒子之间信息的交互,这类演化模式按照粒子之间的交互规则可以分为3种类型:离散模型(Discrete Opinion Model)[5]、连续模型(Continuous Opinion Model)[6]、离散连续模型(Continuous Opinions and Discrete Actions Model,简称CODA模型)[7]。离散模型主要有Sznajd模型[8]、投票者模型(Voter Model)[9]、多数决定模型(Majority Rule Model)[10]等,在离散模型中,观点的取向一般为一组对立的观点,如是和不是、支持和反对、接受和拒绝;连续模型是一种允许个体在一个如[0,1]之间连续的观点区间内进行观点交互的演化模型,常见的连续观点模型主要为DW(Deffuant-Weisbuch)模型[11]和HK(Hegselmann-Krause)模型[12]。在该类模型中,观点的演化准则是建立在有界信任的基础上的,其演化要满足个体观点差值在一定的阈值之内这一条件;CODA模型是建立在离散模型和连续模型的基础上,其观点的交互一般根据贝叶斯准则进行演化,演化过程较为关注邻居的观点,故不能较好地反映个体的主观意愿。二是自上而下的以网络结构为载体的舆论传播模式,这类模式借鉴网络科学的相关知识,以复杂网络结构为载体进行舆论的传播与扩散,具体演化传播模型有SIS(Susceptible-Infected-Susceptible)模型[13]、SIR(Susceptible-Infected-Removed)模型[14]、SIRE(Susceptible-Infected-Removed-Escape)[15]等模型。虽然上述舆论观点演化模型的提出为后续学者研究舆论演化提供了一定的参鉴意义,然而目前鲜有学者基于认知失调(Cognitive Dissonance)[16]这一视角对舆论观点的演化进行研究。事实上,在一定范围内,个体之间的亲和力可以随着观点的演化而发生相应变化,并且亲和力的变化可以有效促使观点发生相应的演化,进而形成认知失调。在认知失调视角下,网络舆论的演化呈现何种规律?如何合理构建健康网络舆论环境,引导网络舆论合理演化,对破解重大舆情危机,疏导公众情绪,维护社会长治久安具有重要的理论与现实意义。
1 网络舆论演化模型构建
在网络舆论演化过程中,HK模型作为个体与群体观点交互的经典模型近年来受到广大学者的广泛关注。该模型在个体观点与周围观点差值小于一定阈值的基础上,依据有界信任准则,进行观点更新。目前,已有学者对HK模型进行了相关改进,以应用于不同的舆论观点演化情境中。文献[17]在非线性系统中采用离散时间分数阶以及考虑个体记忆效应的情况下,对经典HK观点演化模型进行了研究;文献[18]将个体进行分层,引入异质有界信任的概念,在改进HK模型的基础上,对开放型、随和型和封闭型群体人员的观点演化进行了研究;文献[19]在考虑大众传媒和信任范围的多样性的基础上,研究了改进的HK模型和DW模型,研究发现信任范围的多样性可以提高系统达成共识的能力。上述学者基于经典HK模型,对HK模型进行了相关改进,研究了不同舆论观点的演化问题,取得了一定的研究成果,然而鲜有学者基于认知失调视角,将个体之间的亲和度引入到HK模型,较为完备的研究网络舆论的演化。
1.1 HK模型
假设系统中存在N个个体,个体的观点可以在一维欧几里得实数空间R内用一个实数进行表示,定义集合Ω={1,2,…,n}中的某一个体i∈Ω的观点可以表示为oi(t)∈R,设置ε={ε1,ε2,…,εn}为观点影响阈值(个体信任阈值),每个个体将会按照式(1)在观点影响阈值εi内与其周围邻居进行观点交互。
(1)
其中,Ni(t)={j∈V||oj(t)-oi(t)|≤εi}表示个体i在t时刻时周围的邻居个数;uij为个体j对个体i的观点的影响程度,uij=0表示周围个体对个体的观点没有影响,个体的观点较为坚定;uij=1表示个体的观点完全受周围个体影响,而与自身观点无关。
1.2 改进HK模型(EHK)
在网络舆论演化过程中,人与人之间的亲和度往往会对观点的演化产生一定的影响,进而形成认知失调,在关系较好的两个体中,观点的真实性以及个体对观点的坚持度较个体之间的亲和度而言往往显得不是特别重要,为了准确刻画认知失调对群体观点演化的影响,本文引入亲和度这一指标对基本HK模型进行改进,形成了改进的HK模型(Extended Hegselmann-Krause,简称EHK)。

(2)
(3)
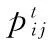
(4)
此处,η为亲和度阈值,η∈[0,1]。对上述个体之间的权重进行标准化处理,得到周围群体对个体i的影响权重为:
(5)
基于上述定义,对HK模型进行改进,得到改进的HK模型(EHK)如下:
(6)
其中,g(i)表示个体对初始观点的坚持度,g(i)=0表示个体对观点的判断全部受周围个体的影响,没有发挥自我的主观判断力,g(i)=1表示个体对观点比较偏执,不容易受周围人的影响;Θ表示周围群体对个体i的影响权重;Ni(t)表示t时刻系统内的个体数。
2 认知失调视角下网络舆论演化仿真及分析
2.1 初始观点坚持度与网络舆论演化仿真及分析
初始观点坚持度,即个体对观点的初始倾向。一般来说,大多数个体的初始观点是随和的,也有少部分个体的观点倾向是极端的,为了探究初始观点坚持度对观点演化的影响机理,本文在初始观点坚持度满足正态分布、均匀分布、随机分布的情况下,探究了初始观点坚持度对观点演化的影响,其中参数设置取个体数N=1000,演化次数t=1000,亲和度阈值η=0.8,观点影响阈值ε=0.5;正态分布的均值δ=0.5,方差σ=0.1,其余参数保持不变,利用Matlab软件进行仿真演化得到不同分布条件下观点的演化结果如图1所示。
在图1中,可以发现,在随机分布条件下,观点的演化收敛时间最长,大约在450次完成收敛;在均匀分布条件下,观点收敛时间次之,大约为300次;在正态分布条件下,观点的演化收敛时长最短,大约为40次。这一结果表明在均值的正态分布条件下即初始观点坚持度处于中立状态时,观点的演化过程较均匀分布和随机分布更容易形成一致。这一结果也与现实较为吻合,在现实生活中,当群体中含有较少偏执个体时,大众观点会快速向偏执观点进行靠拢,观点容易在较短时间内形成一致,从而达成观点共识。
以正态分布为例,本文在均值分别为δ=0.1,δ=0.3,δ=0.5,δ=0.7,δ=0.9,方差σ=0.1情况下进一步探究了舆论的演化收敛时长,具体如图2所示。
由图2可知,在不同均值的正态分布条件下,观点的演化时长也不相同,随着均值的增大,观点演化时长也在不断增大,当δ=0.1时,观点发生收敛的演化时长为19;当δ=0.5时,观点发生收敛的演化时长为39;当δ=0.9时,观点发生收敛的演化时长为425。由此可知,观点的演化时长与群体中观点的均值密切相关。若群体大多数观点是随和的,观点坚持度较低时,观点较为容易发生演化,形成一致观点;若群体中大多数观点是偏执的,观点的坚持度较高时,观点不容易发生演化,从而形成分散的观点,具体如图3所示。
2.2 异质信任水平与网络舆论演化仿真及分析
在社会群体中,个体与个体之间的信任水平是不相同的,即个体之间的信任水平是异质的,为了探究异质信任水平下网络舆论的演化情况,根据个体的信任水平将个体划分为偏执型、随和型、开放型个体,假设其信任区间分别为[0.01,0.05]、[0.2,0.3]、[0.4,0.9]。在初始观点服从均匀分布和正态分布(δ=0.5,σ=0.1)的情况下,本文探究了异质信任水平对网络舆论演化模式的影响,舆论演化结果如图4所示。
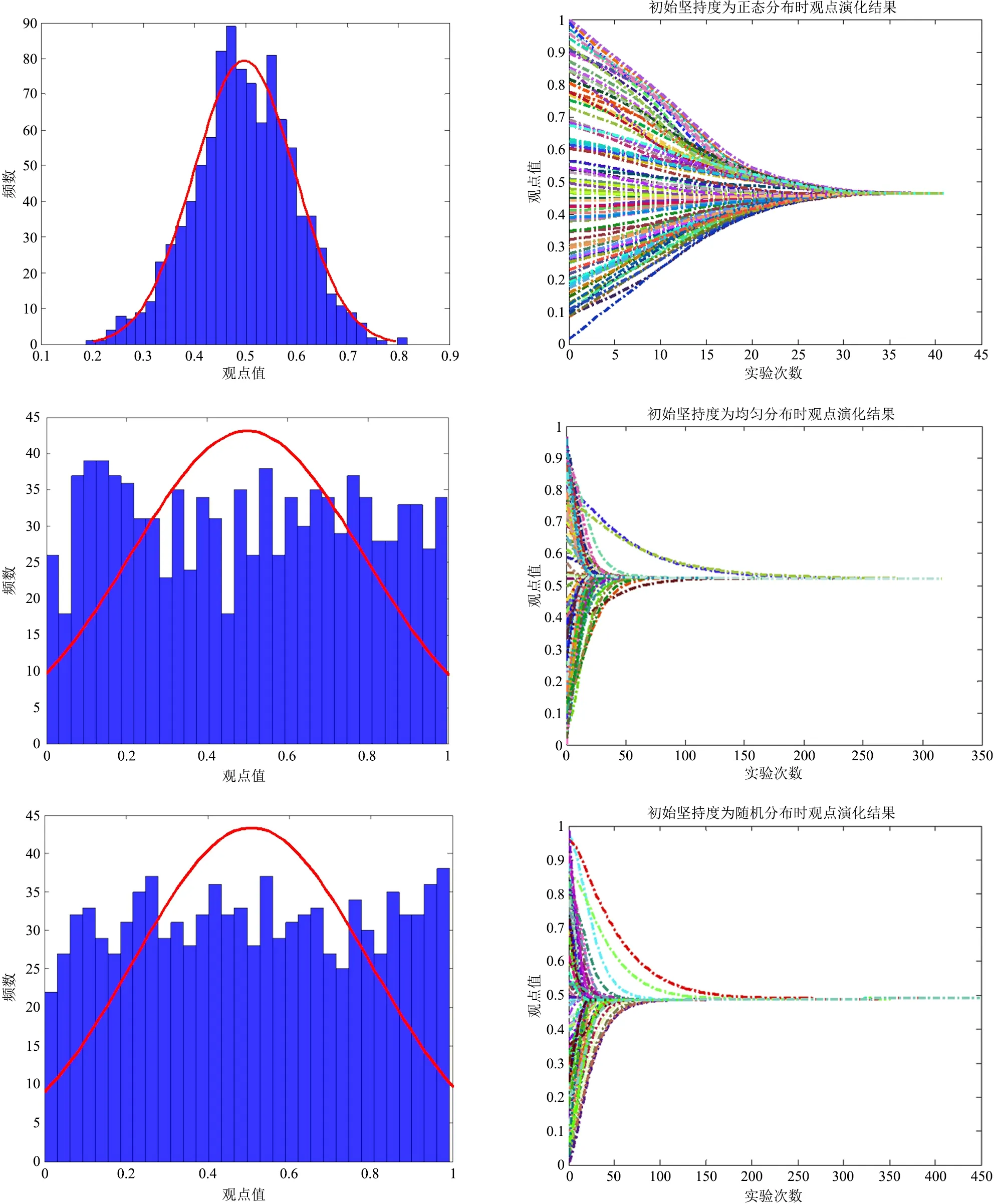
图1 初始观点坚持度服从正态分布、均匀分布、随机分布的观点演化结果
在图4中,图a、c、e是初始观点服从均匀分布的情况下舆论的演化结果,图b、d、f是初始观点服从正态分布情况下舆论的演化结果。对比图a、c、e可以发现,舆论的极化或者分裂会根据不同的信任水平而发生相应的变化,在初始观点服从同一分布时,开放型个体较偏执型和随和型个体更容易形成一致观点。此外,对比图a、b以及图c、d可以发现,在不同的初始观点分布条件下,同一类型的个体也会促使观点舆论形成不同的演化结果。
2.3 亲和度与网络舆论演化仿真及分析
媒体的碎片化和片面化,以及数字网络的发展让分享变得廉价,让全世界的人成为潜在的参与者。在网民发表观点与评议的过程中,个体与个体之间的亲和度也是影响观点演化的一个重要因素。一般来说,个体之间的亲和度较大时,观点的演化较容易形成一致,不同亲和度对应的舆论演化结果如图5所示。
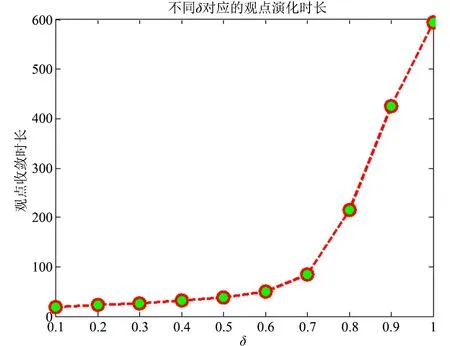
图2 正态分布下不同均值对应的观点演化时长
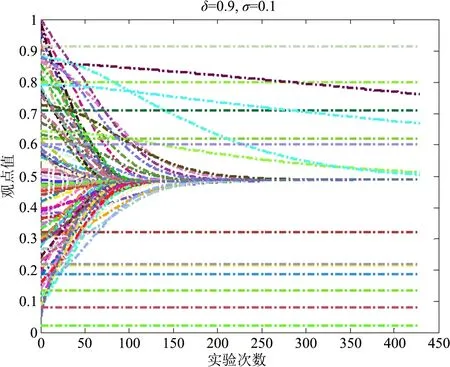
图3 均值δ=0.9、σ=0.1时观点的演化结果
由图5可以发现,当亲和度发生变化时,观点的演化时长和观点的收敛状况也发生了变化。当个体间的关系度为0.05时,演化结束时,观点簇的个数为5个,观点演化时长为38;当个体间的亲和度为0.1时,观点的演化时长缩短为32;当个体间的亲和度继续增大为0.3时,观点的演化时长缩短为29;当个体间的亲和度增大为0.5时,观点的演化时长缩短为28,观点簇的个数由5个变为4个;当个体间的亲和度增大到观点阈值0.8时,观点的演化时长缩短为27;当个体间的亲和度增大到1时,观点的演化时长虽然变长,观点簇的个数为1个,观点此时形成一致。上述研究表明,在观点阈值内,随着个体之间的亲和度的增加,观点的演化时长会逐渐缩短,并且观点簇的个数也会发生变化,当个体间的亲和度大于观点阈值时,观点会发生收敛,形成一致。
2.4 观点阈值与舆论演化仿真及分析
观点阈值作为有界信任的阈值指标对观点的演化具有重要的作用。为了探究观点阈值对舆论演化的影响程度,在亲和度Xij=0.5,亲和度阈值η=0.8,初始观点服从正态分布的(δ=0.5,σ=0.1)的条件下,选取观点阈值ε=0.05,ε=0.1,ε=0.25,对观点阈值对舆论演化的影响机理进行了研究,具体演化结果如图6所示。
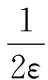
3 案例分析
为了真实的验证本文所构建模型的准确性,本文选取了2015年成都女司机被打事件进行案例分析,以从侧面说明本研究的合理性。
3.1 事件描述
2015年5月3日下午,在成都市娇子立交处,一名男司机将一女司机逼停后当街殴打,性质恶劣,随后警方公布一段行车记录视频,起因女司机突然变道影响到男司机行车随后双方有斗车行为,差点酿成车祸。这段视频公布后引发数万网友转发,数万网友谴责女子被打不冤。2015年5月4日,锦江公安分局成龙路派出所针对“男司机逼停殴打女司机”事件做出通报。在警方出示的案件询问视频中,伤人司机张某表示,他对自己的行为感到非常后悔,一时冲动,铸成大错。2015年5月11日,被打女司机卢琴发表了致歉信,在信中她称她将痛定思痛,认真的反思,并对大家表示歉意,并称自己十分内疚。具体的舆情进展如图7所示,图中横轴表示时间轴,框内的内容表示舆情事件的进展。
3.2 事件分析
在2015年成都女司机被打事件中,充分说明了认知失调以及个体之间的亲和度可以促使舆情发生了变化以及逆转。具体而言,在女司机被打这一事件发生后,公众的第一反应就是男司机“素质差”,“变态”,“丧心病狂”,之所以这种负面评论指向男司机,是由于公众受传统潜意识(女性在生理上属于弱势群体)影响,导致公众与女司机的亲和度较大,从而发生了认知失调,认为男司机不应该或者不能打女司机。此外,由于政府或者公安机关在较短时间内,没来得及公布事情真相,导致公众的初始观点坚持度较大,观点不容易改变,认为男司机在这起事件中,不应该打女司机,男司机打人应该负全责,进而导致男司机要承受一定的舆论压力。这一现象也验证了本文2.1部分初始观点坚持度越大,其观点越不容易发生改变这一结论。
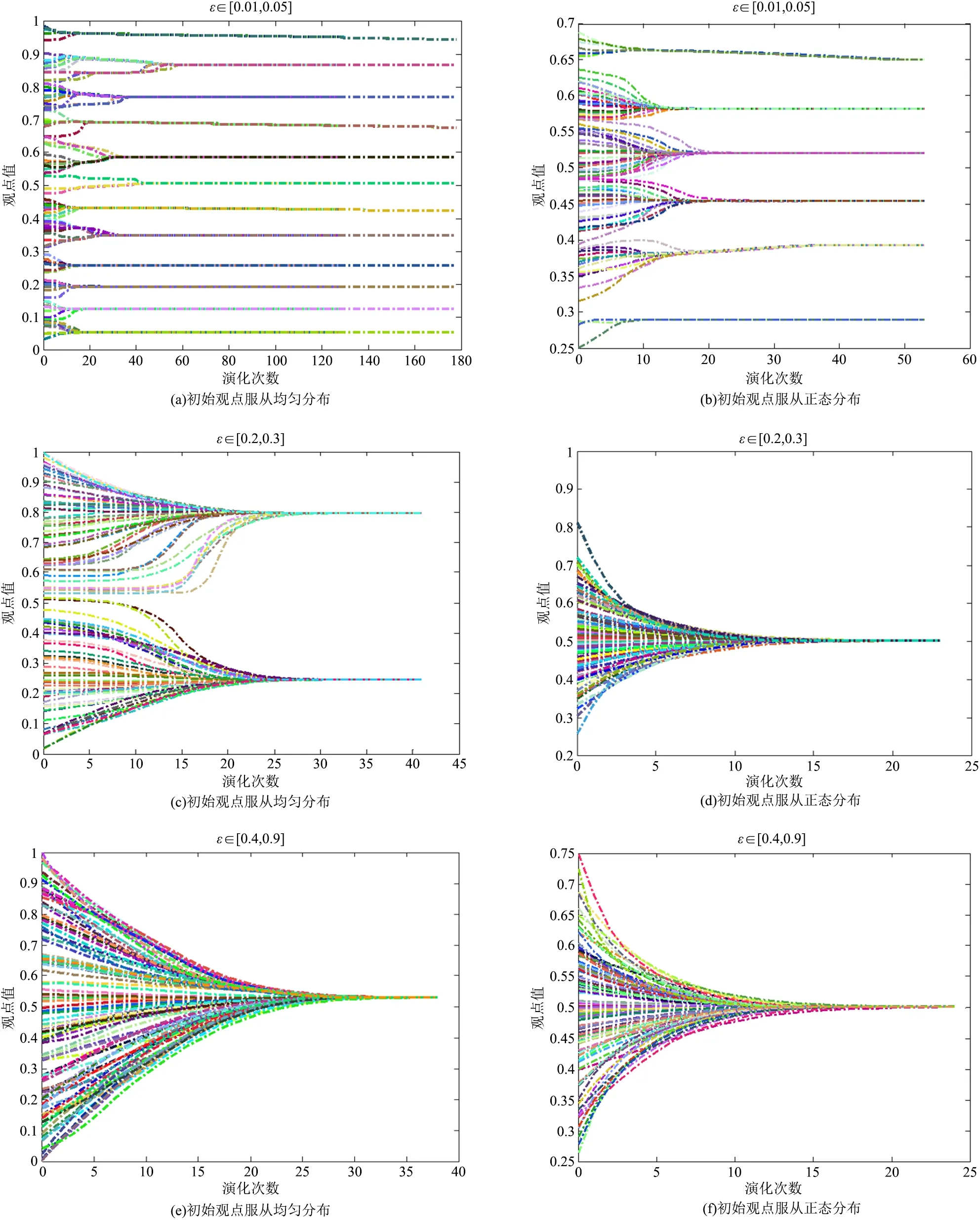
图4 异质信任水平下基于改进HK模型的观点演化结果
在这起事件中,网友的观点褒贬不一,有反对的、中立的以及支持的。这些观点的出现表明在受众群体中,个体是分层的,不同的个体可能具有不同的舆论态度。就偏执型群体来说,其对观点的坚持度较大,故其言论也带有一定的偏执性,不容易形成一致的舆情,这一现象也验证了本文的2.2部分异质信任水平与网络舆论演化密切相关这一结论。
事件发生后,3日晚间,张某的行车记录仪曝光,4日舆论迅速发酵,此时,公众在发现事情的真相后,舆论开始向男司机倾斜。公众与男司机的亲和度在不断增加,与女司机的亲和度在不断减小,尤其当发现女司机是个违章多次的司机时,这更加提升了公众对这一事件的认知程度。在这一过程中,公众与男司机亲和度的增加促使舆论的走向逐渐偏向男司机,这种认知失调促使公众给予男司机更多的支持,而与女司机的亲和度的下降促使公众逐渐偏离女司机。这一现象充分说明了亲和度可以促使公众发生认知失调,这种认知失调可以让舆论发生逆转。此外,公安机关在发布行车记录仪相关视频以后,公众的认知程度得以提升,对事件的真相有了进一步的了解。此时,公众的观点阈值也逐渐变大,不同意见逐渐减少,形成支持男司机的一致意见,这一现实现象与本文2.3和2.4部分的相关研究结论不谋而合。
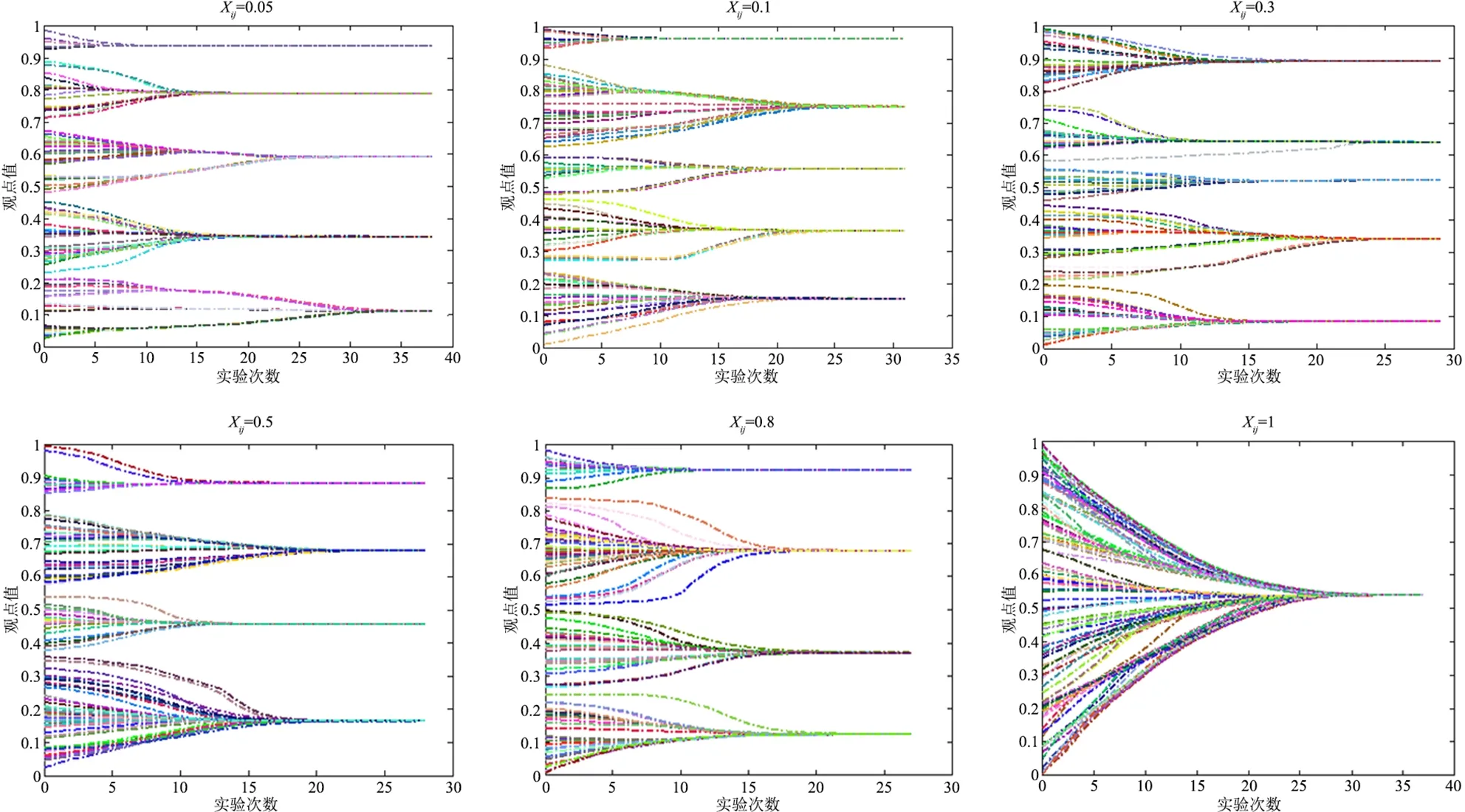
图5 不同亲和度下观点的演化结果
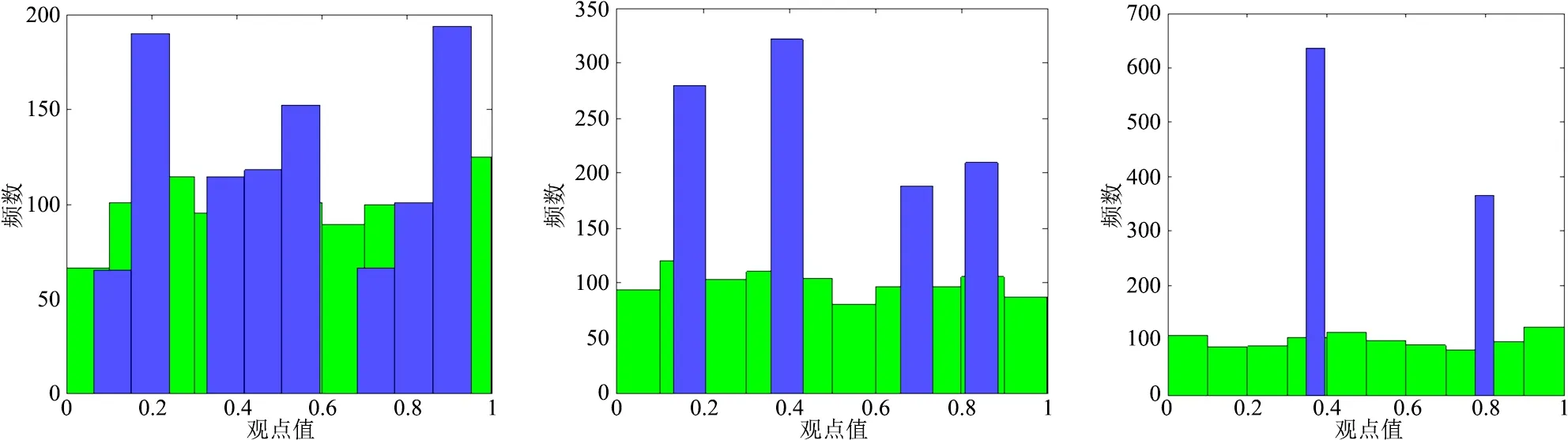
图6 观点阈值ε=0.05、ε=0.1、ε=0.25条件下舆论的演化结果
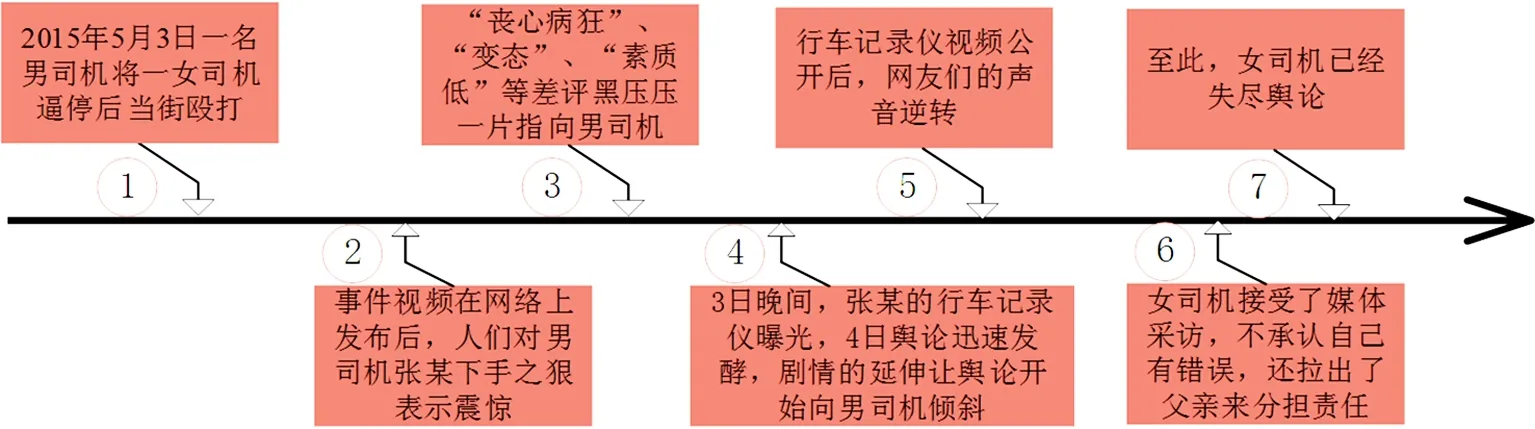
图7 成都女司机被打舆情进展图
4 认知失调视角下舆论演化干预策略
在认知失调视角下,不当的干预策略可能会助长网络舆论的气焰,使得重大舆情得不到有效干预和控制。为了避免舆论在演化的过程中,出现失控、泛滥的局面,基于上述研究,拟从以下几种途径来对舆论演化进行干预,以实现舆论稳定,和谐演化的最终目标。
4.1 及早公布事实真相,减少信息的不对称程度,降低舆论认知失调效应
如何改变受众群体的观点坚持度、澄清事情真相、降低舆论的认知失调效应是在应对舆情危机时必须要考虑的一个因素。当发生重大舆情时,政府要准确快速向大众做出回应,防止公众的认知以及对观点的坚持度仍停留于初始水平,若不能及早将事情的真相公布于众,就会对政府的公信力以及公众的情感造成一定的损伤。当公众的观点坚持度小于0.5时,此时是进行舆情引导的绝佳时机;当公众的观点坚持度增长为0.9时,此时较难引导舆论走向,同时也较难把控公众的情绪。在天津滨海新区化学品爆炸事件中,政府没有及时将事实的真相向大众公布出来,反而逃避责任,以“不明白”和“不明确”的态度回应此事,推脱责任。在这样的情形下,公众认为政府不作为的观点逐渐增强,最终即使政府后来对此事件进行了解释,也难以挽回公众对政府的信任,从而造成了不可避免的舆情事件。
4.2 制定个性化的舆情疏导策略,因人施策,多渠道引导舆论向平稳状态过渡
不同的个体对观点具有不同的态度,如何个性化的实施舆情导向作用,从而使得受众群体的情绪能够快速缓和,舆情得到有效控制,是舆情处理部门不得不考虑的一个重要问题。群体是由多个不同类型的个体构成,故在发生舆情时,由于个体类型的多样性(异质性),舆情一般也呈现一种多样性。偏执型、随和型以及中立型个体都会表达自己对某件舆情事件的观点,这些观点褒贬不一,众口难调,其中偏执型个体(ε∈[0.01,0.05])的观点较难发生改变,开放型个体(ε∈[0.4,0.9])的观点较为容易发生改变。在成都女司机被打事件中,有的个体会认为女司机被打很冤,也有个体为女司机被打叫好,大部分个体对此事件保持中立,这就导致这起舆情事件较难形成一致共识,一时争吵不断。此时舆情处理部门就应该因人施策,采用个性化的舆情疏导策略,对受众群体进行个性化引导,从而使得舆情得以尽早控制。
4.3 采用合理的方式方法,晓之以理,动之以情,正确处理舆情危机
亲和度和观点阈值的改变都可以影响观点的收敛时长,较大的亲和度和观点阈值可以使得舆论的演化时长快速缩短,甚至可以使得舆论观点从分散走向一致。公众和政府人员作为一种社会群体,个体与个体之间的亲和度会随着事件的进展和处理方式方法的变化而发生变化。发生重大舆情时,政府要采用合理的方法,晓之以理、动之以情,要在处理重大舆情事件中,要给予公众更多的人文关怀,这样可以促使公众与政府的亲和度得以增加,若亲和度大于亲和度阈值(Xij>0.8)时,亲和度较观点阈值来说,对观点的影响作用更大,这样可以有效促使观点从分裂走向一致。
5 研究不足与展望
在认知失调视角下,本文基于经典HK模型,将影响舆论演化的亲和度这一现实因素考虑到HK模型中,构建了改进的HK舆论演化模型,在此基础上,探讨了初始观点坚持度、异质信任水平、个体之间的亲和度、观点影响阈值对网络舆论演化的影响,并以2015年成都女司机被打事件为例,对本文的研究进行了案例分析。最后基于上述研究,提出了网络舆情干预策略,以期为政府解决重大舆情事件提供一定决策依据。研究具有一定的现实意义,然而也具有一定的局限性,那就是本文没有考虑网络结构,以及个体间关系的进化对舆论演化的影响,未来可围绕此方向结合多种舆论演化模型进行进一步的研究。
[1]中国网信网.CNNIC发布《第40次中国互联网络发展状况统计报告》[EB/OL].http://www.cac.gov.cn/2017-08/04c_1121427672.htm,2017-11-27.
[2]李萍.从群体极化视角谈网络舆情危机的预警之策[J].现代情报,2015,35(4):61-64.
[3]汪明艳,陈梅,Zhu Y B,等.社交媒体舆论演化下个体观点交互的可信度研究[J].现代情报,2017,37(1):57-65.
[4]王晰巍,邢云菲,张柳,等.社交媒体环境下的网络舆情国内外发展动态及趋势研究[J].情报资料工作,2017,(4):6-14.
[5]Gambaro J P,Crokidakis N.The Influence of Contrarians in the Dynamics of Opinion Formation[J].Physica A-Statistical Mechanics and Its Applications,2017,486:465-472.
[6]Holzer M,Khatri,R.Pattern Formation,Traveling Fronts and Consensus Versus Fragmentation in a Model of Opinion Dynamics[J].Physics Letters A,2017,381 (37):3197-3202.
[7]Martins A C R.Discrete Opinion Models as a Limit Case of the CODA Model[J].Physica A-Statistical Mechanics and Its Applications,2014,395:352-357.
[8]Lima F W S.Transition Under Noise in the Sznajd Model on Square Lattice[J].International Journal of Modern Physics C,2016,27(3):1-8.
[9]Vieira A R,Crokidakis N.Phase Transitions in the Majority-Vote Model with Two Types of Noises[J].Physica A-Statistical Mechanics and Its Applications,2016,450:30-36.
[10]Lian Y,Dong X F,Liu Y J.Topological Evolution of the Internet Public Opinion[J].Physica A-Statistical Mechanics and Its Applications,2017,486:567-578.
[11]Borra D,Lorenzi T.Asymptotic Analysis of Continuous Opinion Dynamics Models Under Bounded Confidence[J].Communications on Pure and Applied Analysis,2013,12(3):1487-1499.
[12]Su W,Gu Y J,Wang S.et al.Partial Convergence of Heterogeneous Hegselmann-Krause Opinion Dynamics[J].Science China-Technological Sciences,2017,60(9):1433-1438.
[13]Meier,J,Zhou X,Hillebrand A.et al.The Epidemic Spreading Model and the Direction of Information Flow in Brain Networks[J].Neuroimage,2017,152:639-646.
[14]Maroufy E I H,Kernane T,Becheket S.et al.Bayesian Inference for Nonlinear Stochastic SIR Epidemic Model[J].Journal of Statistical Computation and Simulation,2016,86(11):2229-2240.
[15]Chen L H,Wei F Y.Persistence and Distribution of a Stochastic Susceptible-Infected-Removed Epidemic Model with Varying Population Size[J].Physica A-Statistical Mechanics and Its Applications,2017,483:386-397.
[16]Wang S W,Huang C Y,Sun C T.Modeling Self-Perception Agents in an Opinion Dynamics Propagation Society[J].Simulation-Transactions of the Society for Modeling and Simulation International,2014,90(3):238-248.
[17]Dorota M,Malgorzata W.Fractional Discrete-Time of Hegsemann-Krause’s Type Consensus Model with Numerical Simulations[J].Neurocomputing,2016,216:381-392.
[18]Fu G Y,Zhang W D,Li Z J.Opinion Dynamics of Modified Hegselmann-Krause Model in a Group-Based Population with Heterogeneous Bounded Confidence[J].Physica A,2015,419:558-565.
[19]Pinede M,Buendia G M.Mass Media and Heterogeneous Bounds of Confidence in Continuous Opinion Dynamics[J].Physica A,2015,420:73-84.
[20]何建佳,张亚楠.基于关系度的群体观点演化模型与仿真[J].计算机应用研究,2017,34(6):1694-1698.
[21]Fan K Q,Pedrycz W.Emergence and Spread of Extremist Opinions[J].Physica A,2015,436:87-97.
