FCFE模型与蒙特卡洛模拟相结合在公司估值中的应用

常振辉，高 岩

（上海理工大学管理学院，上海200093）

经过三十多年的发展，我国的市场经济迅速发展、资本市场的建设也日趋完善，而资本市场的核心问题就是估值问题。业界内也注意到了对公司价值进行评估的重大意义。特别是在我国经济发展进入新常态的当下，随着去产能的不断深化，越来越多的企业会兼并与被兼并。公司估值已经是公司财务管理、投资决策和收购兼并的重要工具。对于企业而言，以公司价值最大化作为公司经营的战略目标制定相应的财务政策、经营目标有利于公司的健康发展。对于投资者而言挖掘出公司的合理价值有利于对当前的公司股价有一个适当的判断。

1 公司估值的方法

1.1 相对估值法

相对估值法是一种对同类公司进行比较的方法，该方法认为某项资产的估值来源于同类型可比较的其他资产的定价。由于相对估值法简单直接，因此实际中大多采用此种方法。它包括市盈率、市净率[1]等方法。

①市盈率是指每股市价与每股收益之间的比率，即股价/每股收益，它代表了投资者为了获得公司每股的收益而愿意支付多少倍的价格。通常来说，如果市盈率小，那么投资者就越有可能在短时间内收回成本进而获得盈利，所以，其他条件相同的情况下市盈率越低的股票越值得买入。而对于一家上市公司来说，高市盈率又意味着投资者对公司的长期前景看好，所以他们愿意在现下付出较高的价格希望能在公司的成长中获利，高市盈率意味着高风险，高风险则对应于高收益。因此在现实的商业社会当中，复杂的商业环境和相互竞争的压力，再加上宏观经济政策、行业周期等因素影响下，上市公司未来的收益存在极大的不确定性，所以单单使用市盈率来对公司估值就会很片面，就会存在很不不确定性影响评估的实际效果。

②市净率是指每股股价与每股净资产之间的比率，即每股市价/每股净资产。一般说来市净率较低的股票，投资价值较高，相反，则投资价值较低。由于会计制度的不同往往使得净资产与境外企业的概念存在着一定的差别，因此对待市净率要动态的看，另外，净资产仅仅是企业静态的资产概念，存在着一定的变数。在评估高风险企业，企业资产包含大量实物资产时较为常用。通过多以上两种相对估值法的分析，我们认为相对估值法在对行业或者具体几家公司之间进行比较时有一定可取之处，但是在分析某家具体公司，对其进行估值时就显得片面和不准确。接下来我们分析绝对估值法。

1.2 绝对估值法

绝对估值法是指将公司的未来现金流进行贴现的现值，包括股利贴现模型（DDM）、公司自由现金流模型（FCFF）、股权自由现金流模型(FCFE)[2]等等。

1.2.1 股利贴现模型（DDM）

投资者购买公司股票是期望能够从公司未来的发展中得到收益，那么投资者在购买股票后可以得到持有期所派发的股息以及持有期末的预期价格。所以股票的内在价值可以用每年股利收入的现值之和来计算：

其中PV代表的是股权价值，Dt表示第t期的股利，r指投资者要求的投资回报率。

1.2.2 公司自由现金流模型（FCFF）

现金流折现模型包括公司自由现金流模型以及股权自由现金流模型都是从股利折现法的基础上不断发展起来的，不同之处在于，股利折现法用的是实际的股利现金流，而现金流量法体现的经济学原理是企业的内在价值应当取决于企业未来所产生的全部现金流量的现值总和。FCFF模型的基本公式如下：

上式中FCFF1表示下一年的预期公司自由现金流。WACC表示加权平均资本成本，G表示公司自由现金流的固定增长率。

由于不同的企业处于不同的发展阶段，呈现出不同的发展特征。发展出不同的阶段性模型，常见的是两阶段模型：一个阶段公司的发展受到多种因素的综合影响，增长率极不稳定，另一个阶段是公司发展已经较为成熟情况逐渐稳定，增长率也开始保持一个稳定的数字。两阶段FCFF模型的基本公式是:

上式中FCFFt表示预期第t年的公司自由现金流，FCFFn+1是指第（n+1）年的公司自由现金流,WACC表示加权平均资本成本，Gn表示n年后的稳定增长率。

对于我国的证券市场而言，公司派现并不具有连续性和普遍性；FCFF评估的是公司的整体价值，综上考虑，FCFE模型更适合用于我国证券市场的公司估值。下面详细介绍FCFE模型的具体估值方法。

2 FCFE估值模型

股权投资者拥有对公司剩余收益的索偿权。公司的经营收入在支付经营费用、债务利息和本金、税金以及资本支出后所剩余的现金性质上便是属于股权投资者的现金流即FCFE。

股权自由现金流（FCFE）=净利润+折旧和摊销-资本性支出-运营资本增加额-债务偿还+新发行债务

通常对公司增长率的不同假设，FCFE估值模型也分为稳定增长模型、两阶段增长模型等。

2.1 稳定增长自由现金流模型

在该模型下，公司的增长率保持一个稳定的增长态势，公司的资本性性支出与折旧相互抵消，公司的运营较为平稳，风险可控适中。模型的基本公式为：

式中，PV表示当前公司价值；R表示折现率；G表示稳定増长率；FCFE1表示预期下一年的股权自由现金流量。

2.2 两阶段自由现金流模型

是指估值将增长率划分为两个增速不同阶段，第一阶段是公司以—个较高的増长率增长，第二阶段是公司维持一个不变的増长率增长，模型基本公式为：

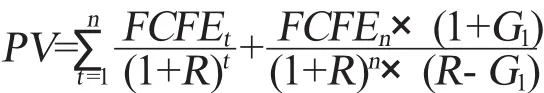
式中，PV表示当前的公司价值；FCFFt表示高速増长阶段第t年的公司股权自由现金流；FCFFn表示高速増长阶段期末的公司股权自由现金流；R表示折现率；G1表示第二阶段时的增长速度。

3 实证分析

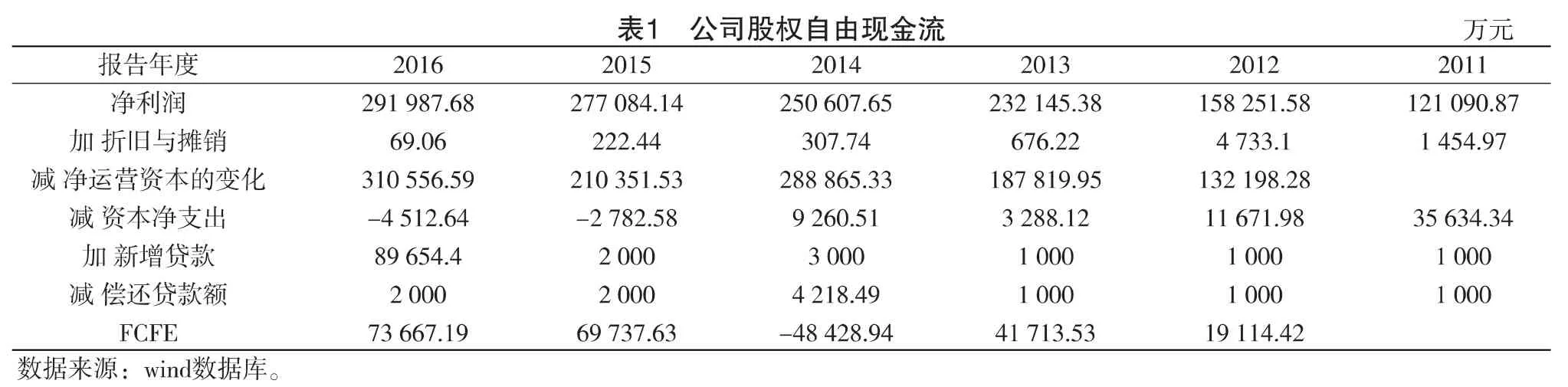
选择云南白药集团股份有限公司（000538）作为我们的研究对像，其上市时间较长数据较为充分，近年来发展比较稳定，在中医药行业属于业内领先。根据公司近五年发布的公司年报得到云南白药的公司股权自由现金流整理如表1所示。

3.1 折现率的估计

折现率是投资者在对企业投资时所要求的投资回报率。本文选择了CAPM模型对折现率进行了计算。在这个模型中，核心的指标有三个，分别为无风险利率、市场的预期收益率以及相对于市场的系统风险系数。模型的公式为：

?

公式中Rf代表无风险利率，Rm代表市场的预期收益率，β代表企业相对于市场的风险系数。

在金融市场中，国债利率不存在违约的风险，所以我们可以用十年期的国债利率近似的代替无风险利率。在2016年，我国财政部共发行了四期十年期附息记账式国债，票面利率分别为2.85%、2.90%、2.74%、2.70%.我们采用算数平均法计算得到平均票面利率为2.80%.即Rf=2.80%。

?

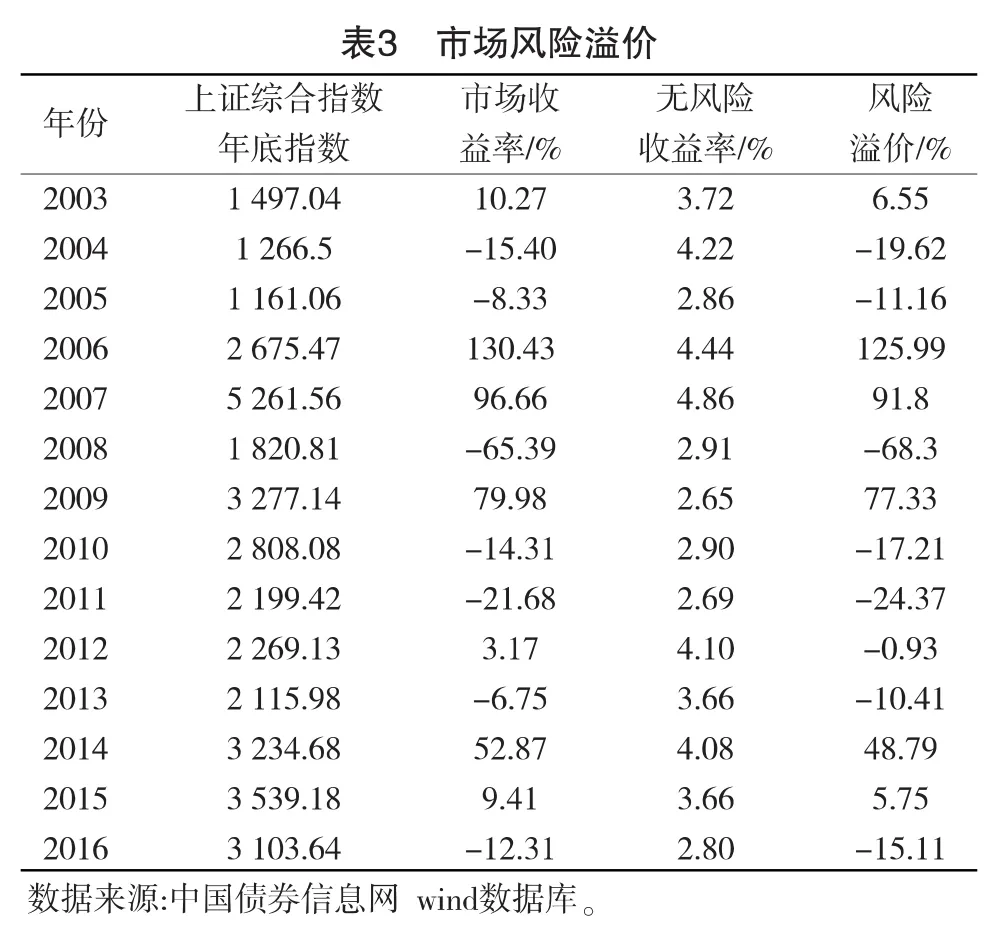
由于上证综合指数建立较早，能够很好的反应我国资本市场的整体情况，因此我们采用上证综合指数每年末的收盘价来计算市场收益率，用当年的十年期国债作为无风险利率。早期的资本市场受到诸多限制的影响，本文采用2003—2016年的数据以反应更加真实的市场情况，通过计算后得到市场风险溢价如表3。

表中市场风险溢价等于市场收益率与同期无风险收益率的差值。根据上表我们用几何平均数法计算市场风险溢价得到（Rm-Rf）=8.43%。

对于公司的β值，用线性回归的分析方法进行估计，以云南白药自上市以来的股价年收益率用变量Y，以上述综合指数收益率为自变量X，进行拟合[3]。利用statas数据分析软件可以看出两者成线性关系。拟合结果汇表如表4。

从上述统计结果来看结果显著，表中统计结果指标R2=0.226 0，云南白药的风险溢价有22.6%来自由市场风险，其他风险来自于公司特定风险。由分析可得回归系数β=0.387。

将以上各个参数代入CAPM模型R=Rf+β×（Rm-Rf），可以得到折现率R=2.80%+0.387*8.43%=6.06%。

?

3.2 增长率的估计

本文运用的是两阶段的FCFE模型，即在未来五年之内，公司以一个较快速度的增长率增长，在第六年之后以一个较慢的增长速度持续增长。随着我国经济结构的不断调整，不再以粗放的增长模式发展，而是进入到了更加健康可持续的经济新常态，我们利用近几年的GDP增长率作为公司高速增长阶段的增长率更具有说服力。

采用算数平均法计算得到高速阶段的增长率G0=8.04%，参照发达经济体的经济状况，通常医药行业在经历过高速增长后可以保持一个较为平稳的永续增长，本文认为永续增长率可以达到G1=5%。

4 引入蒙特卡洛模拟

蒙特卡罗方法被称为统计模拟法或者随机抽样技术，是一种以概率和统计理论方法为基础的一种计算方法，将所要解决的问题与设定的概率模型相联系，利用计算机实现统计模拟或抽样，从而获得问题的一个近似解[4]。

根据以上的分析估算，已经找到了求解两阶段FCFE模型的各个参数，包括公司的股权自由现金流FCFE、折现率R、增长率G1和G0。我们将这些参数代入公式即可求解出公司的估值，但是我们也要知道市场是具有很大不稳定性的，我们所求解出的各个参数可能一个或几个在未来期间发生变化，这样会使得我们通过估值模型计算出来的公司价值与实际出现很大的偏离，从而无法对现实经济活动产生好的指导。我们因此引入蒙特卡洛模拟的方法。将两阶段FCFE模型

?

?

?

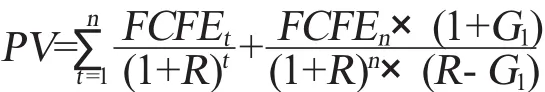
变形为如下模型:

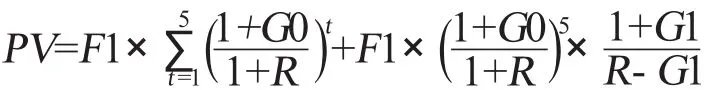
上式中F1为当期的股权自由现金流，G0为高速增长阶段增长率，G1为永续增长率，R是折现率。

然后我们让各个参数在上述的最佳估计数附近取随机数，将值代入变形后的模型当中可以得到一系列的PV值，观察这些PV值并做进一步的统计分析可以很好的找到更符合实际的PV值，对公司价值做出更精准更总体的把握。对各个参数的波动范围及其相应概率设定见表6。

对于折现率R，取7%至9%的概率为0.2，取9%～9.5%的概率为0.6，取9.5%～11%的概率为0.2；对于高速增长率G0，取6.5%～7.8%的概率为0.15，取7.8%～9%的概率为0.55，取9%～10%的概率为0.3；对于永续增长率G1，取4%至4.5%的概率为0.2，取4.5%～5.5%的概率为0.5，取5.5%～6%的概率为0.3。

在matlab软件上实现如下算法，遵照上表的取值规则，计算机每次选取一个R，一个G0,一个G1，代入模型之中会产生一个PV值。计算机选取100个不同的R、G0和G1，则一共会出现一百万个PV值，对这些PV值进行统计得到频率分布图，由于PV值足够多，可以将此频率分布图转化为概率分布图如下：

对上述结果，PV值低于5.0×106和高于1.1×107都属于概率极低的可能性，可以忽略不计，由于模型自身的问题，当折现率与永续增长率取值非常接近的时候就有可能出现较大值，所以我们看到上述分布出现了尖峰后尾的现象。利用matlab编程我们可以得到分布的期望值是8.595 0×106。即得到公司价值PV=859.50亿。

2017年1月1号至8月31号，云南白药的公司市值一直在743.80亿至1 010.30亿范围内波动。由此我们可以看出，利用两阶段的FCFE模型结合蒙特卡洛模拟可以有效的对公司价值进行合理的估计，从而为公司价值管理、企业合并等经济活动起到参考指导作用。

本文的创新之处在于在对公司估值的时候结合了蒙特卡洛模拟，将市场的不确定性考虑在内，将FCFE模型中的各个参数调整为在相应的取值范围内对应一定的概率，更加贴合实际的市场情况.同时我们也应该看到不足之处，例如公司的股权自由现金流可能是负的，那么此时就无法利用FCFE模型。在设定各个参数的概率分布时存在一定的主观性。所以在实际的工作当中要更多的结合公司的实际情况否则会存在偏差。在公司估值方面，当选用不同的方法以及参数的选取方法不同时数理的方法所推断出的公司价值也都只是近似的估计。但是在实证的角度来看，本文模型的选择和参数的确定基本是适宜的可行的。

[1]阿斯沃思.达蒙德理,价值评估——证券分析、投资评估与公司理财[M].张志强,王春香译.北京：北京大学出版社，2003．

[2]张宗新.投资学——证券分析与投资管理[M].上海：复旦大学出版社,2010.

[3]李子奈,潘文卿.计量经济学（第三版）[M].北京：高等教育出版社,2010.

[4]杨桦.蒙特卡洛模拟模型在投资决策中的应用[J].中国管理信息化.2012(8):62-64.