基于BP人工神经网络和遗传算法的葛根总黄酮提取工艺优化研究*

石 磊 高卫红 吕莉莉 赖小波

（浙江中医药大学医学技术学院，浙江 杭州 310053）

近年来随着经济发展，国内中药研究人员开始将新技术、新方法应用于中药制剂的生产和制备。中药提取新工艺对提高中药制剂的质量，加快新药开发起着至关重要的作用。因此运用高新技术发展现代中药，是提高中药市场竞争力、中药现代化的重要途径。然而这些新工艺、新技术在应用过程中无疑要涉及到优化问题，其影响因素往往不止一个，所以设计方案也应是多因素的，主要有响应面实验设计［1-3］、正交试验设计［4］、均匀试验设计［5］和因子设计实验等。其中，最常用的响应面试验设计采用回归方程将试验数据进行线性或非线性拟合，生成具体函数表达式，并进一步分析函数以获取最佳提取工艺条件。

然而，现实系统的组成纷繁复杂，数据与数据之间的非线性关系受诸多因素影响。因此，传统的多元回归拟合方法存在其自身属性的缺陷，难以使用数学方法进行精准建模。人工神经网络（ANN）具有信息分布存储、并行处理以及自学习能力等优点，已在信息处理、智能控制、模式识别及系统建模等领域得到越来越广泛的应用［6］。BP人工神经网络是人工神经网络的重要模型之一，其最大特点是可以以任意精度对连续型函数实现任意逼近，因此被大量应用于非线性建模领域。近年来，BP人工神经网络在药剂学、药动学、药物分析研究等方面也有大量的应用。由于人工神经网络是通过调整神经元与神经元之间的权值和阈值进行拟合，不存在具体的函数表达式，因此不能通过传统的优化方式来求解极值［7］。而遗传算法（GA）是一种随机搜索算法，非常适用于处理传统搜索算法难以解决的复杂和非线性优化问题［8］。它以生物界自然选择和遗传基因组学原理为基础，首先将问题的可行解编码表示成染色体，其中每个染色体代表一个个体；其次通过一定的选择、交叉、变异操作生成一定数量的种群，然后根据适应度的好坏从中筛选出一定数量的优秀个体，进行选择、交叉、变异操作逐步更新种群；最后种群经过若干代进化后，达到最大进化代数。此时种群中适应度最高的个体，即为通常寻找的最优解，解码个体即得到所需最优工艺参数条件［9］。

本文为优化葛根总黄酮的提取工艺，首先利用响应面试验设计获得的数据优化BP人工神经网络模型各参数，建立相应网络模型。然后结合遗传算法通过网络进行极值寻优，获得提取工艺的最佳条件。通过分析BP人工神经网络模型的拟合度和葛根总黄酮得率的预测结果，表明本文算法性能优于使用多元非线性回归算法性能，可用于优化葛根总黄酮提取工艺。

1 BP人工神经网络构建

1.1 响应面试验结果 见表1。本文选用结合超声辅助法的响应面试验设计得到的数据对葛根总黄酮的提取工艺进行优化，并以超声时间、液料比和超声温度这3个因素作为考察条件，以总黄酮得率作为指标，依据公式转移率＝［测得的葛根素质量/称取的葛根质量］×100%［10］。

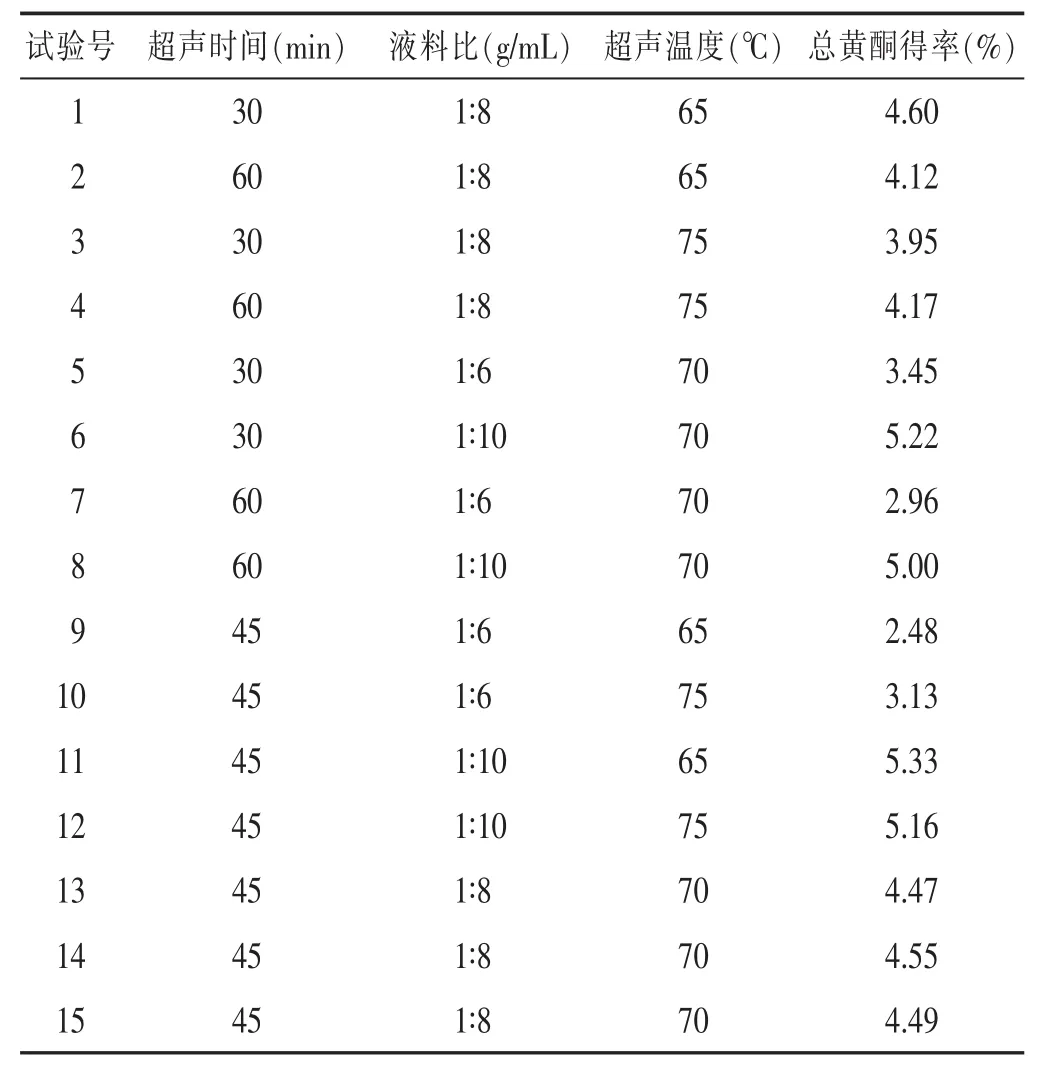
表1 葛根总黄酮的响应面试验结果

1.2 BP人工神经网络的构建和训练 见图1～2，表2。BP人工神经网络是在输入层与输出层之间增加若干（1层或多层）隐藏层，而单隐层（仅包含1个隐藏层）的人工神经网络已经能够逼近任意有理数，具备强大的非线性映射能力［11］。因此在本文实验中，采用3层BP人工神经网络结构对实验数据进行拟合和预测。此外，在本文实验中，以响应面试验设计中影响葛根总黄酮得率的主要因素作为所需BP人工神经网络模型的输入层，输入层的3个节点分别为提取时间、液料比及超声温度，而网络输出层的输出节点对应葛根总黄酮得率，训练数据使用响应面试验的15组数据，将响应面试验中的工艺验证数据作为测试数据。利用Matlab R2008a版软件编写程序，设置隐藏层的传递函数为双曲正切传递函数（tansig），输出层传递函数为线性传递函数（purelin），隐藏层数为1。通过选取不同的隐藏层神经元个数进行拟合比较，最终确定最优隐藏层神经元个数为4。BP人工神经网络的训练算法采用Levenberg-Marquardt（trainlm），该算法结合了牛顿法与梯度下降法，其优点：在网络权值较少的情况下，收敛速度较快，迭代次数更少且精度更高。设定网络训练时的各个参数值：最大迭代次数为200，训练的目标收敛精度为0.01，其他参数均采用Matlab人工神经网络工具箱中的默认值［12］。训练前使用mapminmax函数对各数据进行归一化处理，采用均方误差（MSE）评估BP人工神经网络模型的性能，训练过程。

图1 BP人工神经网络训练误差曲线

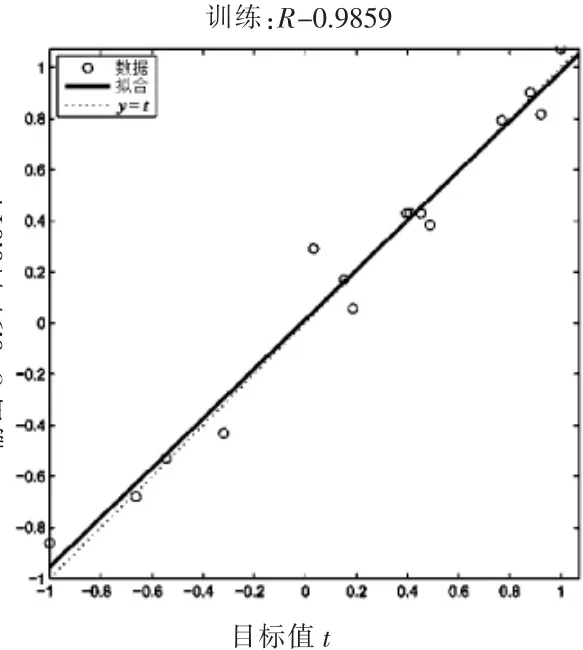
图2 BP人工神经网络拟合图

从图中可以看出，经过13次训练后，网络训练的均方误差已达到所设误差值，且低于最小目标值。接着，采用Matlab人工神经网络工具箱中的sim仿真函数对测试样本进行预测。通过分析测试结果，发现人工神经网络模型的预测性能较好，网络的预测值与实际值的相对误差低于1%。如图2所示，图中有一条实线和一条虚线，实线为理想回归直线，代表网络输出与目标输出的重叠部分，虚线为最优回归直线，代表了实际相似性关系。可以从图中看出，实验数据基本集中在两条直线的重叠区域，理想回归直线和最优回归直线重合度较高，相关系数R＝0.9859，说明该网络的拟合效果和预测性能都较好。经过训练后的BP人工神经网络模型具有良好的预测能力，适用于葛根总黄酮得率的预测。将网络预测结果的数据反归一化，与使用多元非线性回归拟合所得结果相比较，如表2所示。

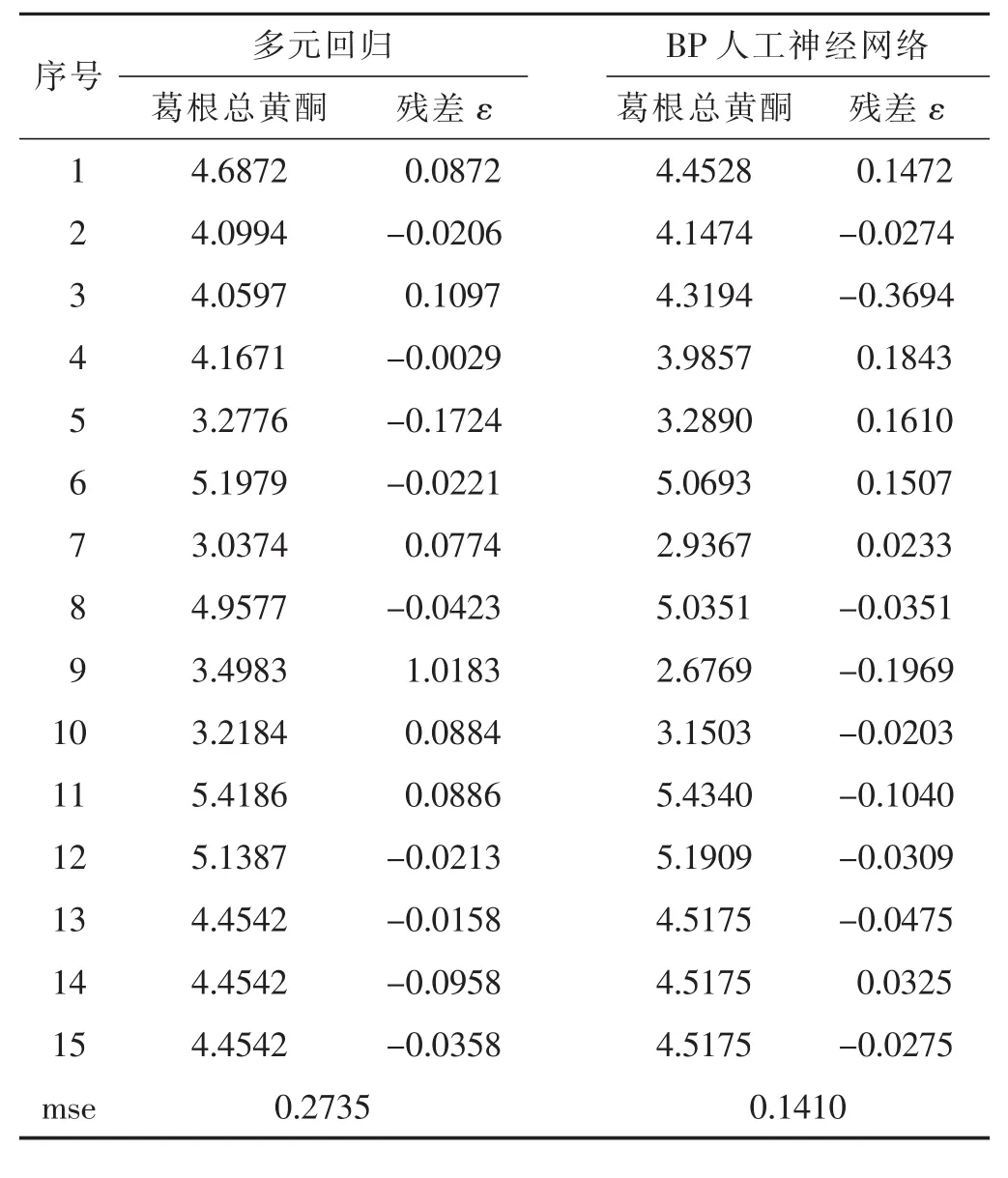
表2 人工神经网络和多元回归的拟合结果

从表2可以看出，BP人工神经网络的拟合效果优于多元非线性回归效果，多元回归的相关系数仅为R＝0.9455。此外，将经响应面试验优化后得到的响应预测值为5.36%，回代验证得到葛根总黄酮得率为5.28%，预测的相对误差为1.49%。而BP人工神经网络在此条件下得到的预测值为5.33%，预测的相对误差仅为0.94%。由此可见，BP人工神经网络不仅在拟合精度上要优于多元非线性回归，其预测的精度也要高于多元非线性回归。通过拟合后比较各自结果可知，BP人工神经网络对响应面试验的各种参数组合都能达到较为准确的预测。

2 结合遗传算法非线性极值寻优

见图3～4。BP人工神经网络结合遗传非线性算法极值寻优主要分为2个步骤，第1个步骤为BP人工神经网络的数据拟合，第2个步骤为遗传算法的极值寻优［11］。

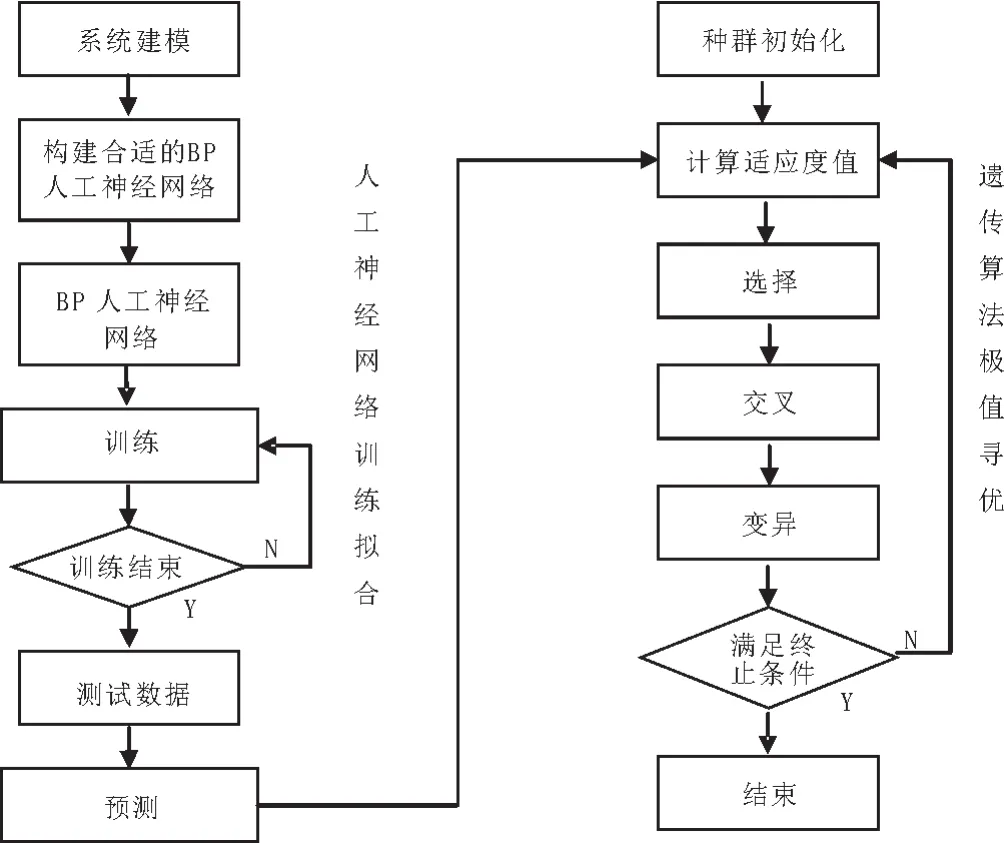
图3 遗传算法极值寻优流程图

图4 葛根总黄酮种群均值变化

以训练完成后的预测结果（葛根总黄酮得率）的相反数作为个体适应度值，根据适应度值的大小，从每代个体中选择一定数量的优秀个体，通过交叉、变异寻找全局最优解以及相对应的输入参数。初始种群个数设为30，最大遗传进化代数设为50，代沟（GGAP）设为0.9，构建区域描述器时每个输入参数的范围分别为［30，60］，［1/10，1/6］，［60，75］，单点交叉（xovsp）概率设为0.7［13］。种群均值含量迭代变化图如图4所示，从图中可以看到，当种群迭代10次后，目标含量的变化逐步趋于平缓，迭代40次后达到稳定。运行程序可以看到，葛根总黄酮的提取量最大为5.47%，各个相应参数值为超声时间50 min，液料比10倍，超声温度66℃。

3 讨 论

中药的提取工艺往往受诸多因素的影响，如温度、时间、液料比、溶剂浓度等，这些指标参数的单位不尽相同，数量级也不处于同一水平。因此在数据进训练前，一般要进行归一化处理，减小各维数量级之间的差距，避免输入数据（影响因素）和输出数据（葛根总黄酮得率）因数量级差距过大而增大网络预测误差。本文采用的数据归一化公式为（X-Xmin）/（Xmax-Xmin），即数据与最小值之差除以最大值与最小值的差，采用Matlab自带函数mapminmax即可实现换算。

BP人工神经网络工具箱会在训练前随机生成相应的权值和阈值，因此每次训练后人工神经网络的预测值都会有一些细微的差别。为使得每次的预测值都相同，需在人工神经网络训练前加入代码“rand（′state′，0）”，以保证产生相同的初始权值和阈值，保证模型的稳定性［14］。

BP人工神经网络中隐含层节点数的选择至关重要，它将直接影响网络模型性能，如若选择不当会导致网络过拟合，即对训练数据的拟合能力过强，导致降低对测试数据的预测能力。但到目前为止，仍没有相应的指导理论和一种科学成熟的方法来确定隐藏层的节点数，大多凭借使用者的经验来确定，或者通过试凑节点，根据网络的预测性能进行选择。当然也有一些使用经验式，但仅供参考，不一定准确。 如：k=（i+j）1/2+z，其中i为网络中输入神经元的个数，这里为影响因素（超声时间、液料比、超声温度）个数，j为网络中输出神经元个数，这里为指标（葛根黄酮得率）数，z为介于1到10之间的常数。

本文通过响应面试验设计优选后得到隐含层神经元节点个数为4。本文使用遗传算法进行极值寻优，采用Matlab自带的遗传算法工具箱［15］对个体的适应度进行排序，由于工具箱函数默认求解极小值，函数值越小的个体，适应度值越大。而在本文试验中，需要葛根总黄酮得率最大，因此在编程过程中需将模拟仿真的结果进行求反操作，以预测值的相反数作为个体的适应度值。此外，在遗传算法运算前先会产生一定数量的个体作为初始种群，这些个体在设定的取值范围内随机生成，因此每次的迭代结果都会有细微的差距，但这对在全局中搜索较优解并不会产生任何影响。

由上述实验可知，通过BP人工神经网络结合遗传算法获得的最佳工艺优化条件参数（超声时间50 min，液料比10倍，超声温度66℃）与多元回归得到的最优参数相近，且预测含量要高于多远回归中得到的最佳含量，具有一定的准确性。因此，多元非线性拟合优化中药提取工艺并非唯一途径，基于遗传算法的BP人工神经网络同样可以得到较为精确的结果。通过上述结果的分析，可以看出BP人工神经网络无论是拟合度还是预测精度，其效果都要优于传统的多元非线性回归。通过建立输入参数和输出指标间的网络模型，结合遗传算法，运用其特有的全局搜索功能，在复杂的空间中进行极值寻优，具有较高鲁棒性。在建立复杂的人工神经网络模型后，以此为基础运用遗传算法进行全局搜索寻优，不失为一种优化中药多参数单指标提取工艺的好途径。

［1］Zhong K，Wang Q.Optimization of ultrasonic extraction of polysaccharides from dried longan pulp using response surface methodology［J］.Carbohydrate Polymers，2010，80（1）：19-25.

［2］Ye CL，Jiang CJ.Optimization of extraction process of crude polysaccharides from Plantago asiatica L.by response surface methodology［J］.Carbohydrate Polymers，2011，84（1）：495-502.

［3］何根祥，谭梅英，詹利之.中心复合设计法在半枝莲总黄酮提取工艺中的应用［J］.湖南中医杂志，2017，33（1）：152-153.

［4］邓仙梅，吴燕妮，王淑美，等.正交试验优选干姜中姜辣素的提取工艺［J］.中医学报，2015，30（1）：83-85.

［5］尹雪，孙萍，温学森，等.混合均匀设计法优化白芍提取工艺［J］.中国药房，2016，27（1）：89-91.

［6］Albino V，Garavelli AC.A neural network application to subcontractor rating in construction firms［J］.International Journal of Project Management，1998，16（1）：9-14.

［7］Wang L，Zeng Y，Chen T.Back propagation neural network with adaptive differential evolution algorithm for time series forecasting［J］.Expert Systems with Applications，2015，42（2）： 855-863.

［8］史峰，王辉.MATLAB智能算法30个案例分析［M］.北京：北京航空航天大学出版社，2011：34.

［9］Haupt RL，Haupt SE.Practical genetic algorithms［M］.John Wiley&Sons，2004.

［10］陈雅维，张延萍，周冬菊，等.响应面法优化葛根总黄酮的超声辅助提取工艺［J］.食品科学，2012，33（14）：41-44.

［11］Whitley D.An executable model of a simple genetic algorithm［J］.Foundations of genetic algorithms，2014，2（1519）：45-62.

［12］Demuth HB，Beale MH，De Jess O，et al.Neural network design［M］.Martin Hagan，2014.

［13］Yingjie L，Shanwen Z，Xuwu L，et al.Matlab genetic algorithm toolbox and application［J］.Xian Electric Technology University Publishing，Xian，2005：45-48.

［14］雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005：45-60.

［15］杨铭，汪文娟.BP神经网络结合遗传算法用于丹参提取工艺的多目标优化［J］.药物服务与研究，2007，7（6）：417-421.