中国省域旅游业TFP增长率测算及收敛性分析

张根明 扶 玥

一、引 言

作为我国国民经济战略性支柱产业，旅游业具有耗能低、带动就业能力强、经济效益高等特点，其发展质量对推动国民经济可持续发展至关重要。全要素生产率（TFP）是衡量一个国家或地区的经济增长质量、技术进步和管理效率的一个重要指标，也是供给侧结构性改革的核心。因此，研究我国旅游业的全要素生产率状况对于推动旅游业供给侧结构性改革和实现旅游业的可持续发展具有重要的现实意义。

目前，学界关于旅游业全要素生产率的研究还没能引起足够的重视，研究主要使用数据包络法进行测算（郭悦，2015；赵磊，2013；何俊阳等，2015），且有不少学者得出的结论存在较大的差异（李逸飞等，2014）。数据包络法采用Malmquist投入距离和产出距离函数来定义Malmquist全要素生产率指数，但数据包络法的稳定性较差，易受随机干扰因素的影响。与DEA方法相比，随机前沿法（SFA）在一定程度上消除了随机因素的干扰，可以对模型中包含的误差项进行分解，结论更加稳定。而目前，使用SFA方法对我国旅游业全要素生产率的研究成果还较少，张丽峰（2014）是近年来比较有代表性的研究，该文使用SFA方法对我国1997～2009年旅游业的全要素生产率增长率进行了分析，发现样本期内全国旅游业全要素生产率增长率为7.64%，技术进步做出了主要贡献，技术进步年均增长率为6.99%。但该文未详尽分析影响旅游业生产效率的主要因素，也未对旅游业全要素生产率增长率的空间动态进行分析。

因此，本文基于随机前沿分析法对我国省域旅游业的TFP增长率进行测算和分解，并从省级单位出发对各省的全要素生产率增长率进行收敛性分析。以期尽可能准确估算我国省域旅游业TFP增长率，分析TFP增长率的影响因素和我国旅游业发展的空间动态发展趋势，为提高我国旅游业的全要素生产率，制定缩小各省域旅游业发展差距的政策，实现区域经济协调、可持续发展提供必要的参考。

二、研究方法及数据说明

在讨论随机前沿模型之前，我们首先需要对生产效率（TE）和全要素生产率（TFP）进行概念上的区分。本文以一个简单的投入产出图进行分析（一种投入及一种产出的生产函数），详见图1。在图1中，横轴表示要素投入量，纵轴表示产出量，其中，曲线1、2分别代表两个时期的生产前沿面，可以用来刻画给定技术水平的情况下一定量的投入所对应的最大产出量。对于企业而言，其产出水平处于生产前沿面之上或之下取决于其生产效率。产出水平低于生产前沿面的距离用来表示随机因素及生产无效率。

A点表示生产无效率点，B点与C点表示生产有效率点。TFP可以定义为由原点和产出水平点构成的射线的斜率水平。假如一个企业的生产活动由A点变为B点，则表示TFP水平的提升，同时，生产效率水平也得到了相应的提升。假如是由B点变为了C点，则企业的TFP水平得到了提升，但是生产效率没有改变。而生产前沿面由1变为2，则表示技术水平的提升。

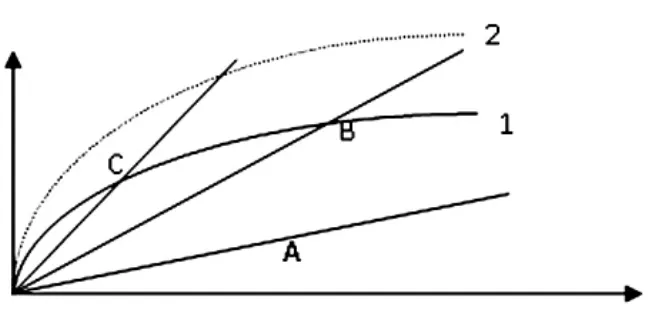
从图1可以看出：全要素生产率的提高可以通过技术进步以及生产效率水平的提升来实现，但是假如技术水平提高的过快，可能会导致生产效率的下降，即可能存在生产率提高与技术水平下降共存的情况。

（一）随机前沿模型

参照Battese and Coelli（1992），随机前沿生产函数模型的一般形式可表示为：

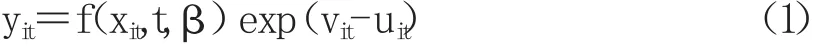
其中，yit是生产者i（1…,N）在第t期的实际产出，（t=1,…,T）。xit为生产所需投入的要素，包括劳动、资本以及二者的平方项和交叉项。f（·）表示生产函数，是随机前沿生产函数中的确定性前沿产出部分。β是有待估计的系数。t表示时间趋势变量，用以测量技术变化。本模型中的误差项为复合结构，由随机误差与技术无效率两部分构成，其中，vit表示随机误差或者其他不可控的随机因素，比如突发事件和气候变化等)。uit表示 i地区在第 t期生产过程中的生产无效率项，且uit≥0，服从半正态分布。按照Battese和Coelli（1992）设定的随机前沿模型，假定时变非效率指数服从：

ui表示技术无效率，其分布服从非负断尾正态分布，即)。参数η表示技术效率指数（-uit）的变化率，假如η>0则说明相对前沿的技术效率在不断改善，否则说明相对前沿的技术效率在不断恶化。

随机前沿生产模型（1）和时变技术非效率指数模型（2）中的参数用最大似然法联合估计得到。似然函数中构造了方差参数：表示技术无效率与随机误差的相对重要程度，当γ=0时，意味着偏离前沿产出完全是由于随机误差造成的，不存在技术无效率；当γ=1时，意味着偏离前沿产出完全是由于技术无效率造成的，与随机误差或白噪音无关。

生产者i相对前沿的技术效率水平（TEit）是衡量实际产出与潜在最大产出的比率。根据Jondrow、Lovell、Materov和Schmidt（1982）提出的混合误差分解方法，从混合误差vit－uit中分离出技术非效率uit。于是

uit存在不同的表现形式，但一般要求其为非负，以确定生产技术效率介于0-1之间，μit为生产无效率项uit的均值。当uit=0时，TE的值为1，表明不存在技术无效率，当uit趋向于正无穷时，TE=0，表明存在完全的技术无效率。其中zit为影响无效率的外生变量，为线性组合，用以研究影响技术无效率的因素。本文将在后文对以上外生变量做以数据说明。λ为需要估计的未知系数。

（二）全要素生产率增长率的分解

根据Kumbhakar（2000）的研究，可以将 TFP增长率分解为：前沿技术进步（FTP）、相对前沿技术效率的变化率（DTE）、资源配置效率（AE）以及规模经济性（SE）。

将方程⑴两边取对数，然后对t全微分得到等式

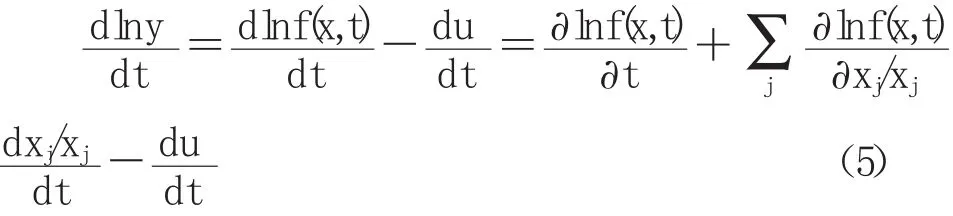
将产出增长率定义为：y＝dlny/dt，前沿技术进步为：FTP＝dlny(x,t)/dt，其衡量的是在保持投入要素不变的情况下产出随时间的变化率，xi＝∂lnxi/dt表示要素 xi的变化率。εj＝∂lnf(x,t)/∂lnxj表示要素 j的产出弹性。那么式（5）可以进一步改写为：

根据增长核算方法，全要素生产率的增长表示为：

这里，sj是要素j在要素总成本中的份额，且有∑sj＝1。根据增长核算方法，在利润最大条件下，要素的产出弹性值应该等于要素的费用份额。通过这个理论依据，我们可以测算出全要素生产率的增长。

将等式（6）代入等式（7），再进行适当变换可得：

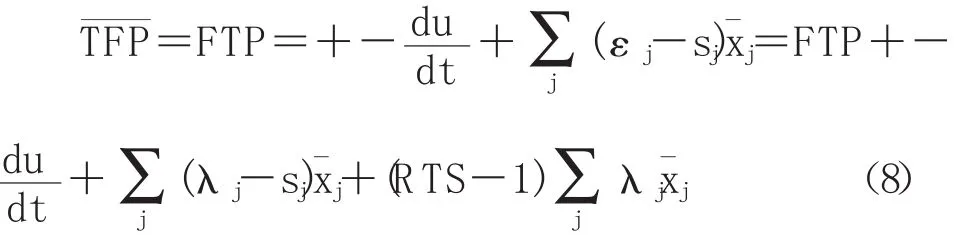
其中 λj＝εj／∑jεj＝εj／RTS 是前沿生产函数中要素j投入的相对产出弹性，有∑jλj＝1。通过这样的转换可以使相对费用份额sj与相对产出弹性λj之间具有可比性，从而可以衡量资源的配置效率。RTS＝∑jεj代表规模总报酬。

等式（8）右边的四项分别表示：

其中，配置效率反映的是要素投入结构的变化对生产率增长的贡献程度。规模经济性反映的是要素的规模报酬对生产率增长的贡献程度。

本文所采用的超越对数生产函数为：

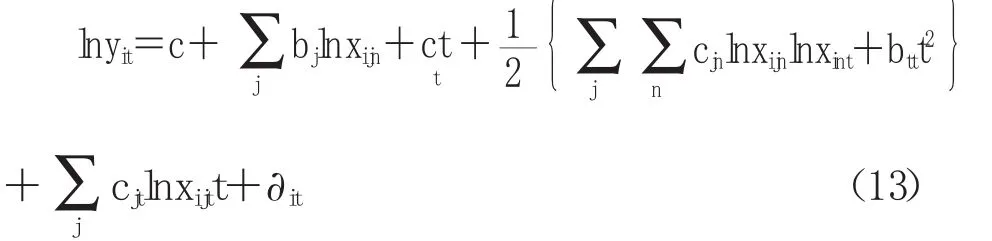
其中，lnyit是第i个地区第t年产出的对数（i=1、2、3…，N，t=1、2、3…，T），lnxijn是第 i个地区第j年第n种投入要素的对数，本文投入要素主要包括资本和劳动两种（j,k=1，2）。T为时间趋势，用来反映技术变化。

（三）数据说明

三、中国旅游业生产效率估计

（一）计量估计中可能存在的问题

在进行TFP增长率分解之前，生产效率（TE）的估计极为重要。复合结构残差项组合vit和uit的分布是相对独立的，均与回归变量无关，这两项残差的联合分布有如下四种情形：正态—半正态（非负），正态—指数，正态—截断正态，正态—伽玛分布，其分布形式会直接影响到生产效率值，并且会引起计量回归估计上的问题。相比传统的最小二乘法，极大似然估计是更加有效的。本文对复合结构残差项的分布采取正态—半正态分布，并采用极大似然估计。已有很多文献运用随机前沿模型估计了生产效率（楚尔鸣等，2013）。但是有一些外生变量无法进入生产函数，却对生产效率具有重要影响。故而建立其他外生变量与生产效率的回归方程进行计量估计，分析引起技术无效率的因素对我们日后提升生产效率的战略选择是十分重要的。早期的相关研究主要使用的是传统两步法估计，即先通过随机前沿模型估计出生产函数和生产效率（TE），再通过方程求解得出无效率项uit，以对其与外生变量建立计量回归模型进行系数估计。但是因为uit为非负项，计量回归时需要使用截断回归。两步估计法也存在着一定的问题（Battese&Coelli，1995）。首先生产函数中的投入要素和回归方程中的外生变量必须不存在相关性，否则遗漏这些关键的变量会导致在第一步生产函数的估计结果是有偏的，进而，会导致第二步计量回归估计结果也是有偏的。

其次，随机前沿模型往往假设无效率项同分布，但是在第二步的生产无效率回归方程中，生产无效率项是随着外部变量变化而变化，这就形成了矛盾（王志刚等，2006）。参照Battese&Coelli（1995）的采用一步回归，利用极大似然估计的方法，可以解决上述问题。Wang,Hung Jen and Schmidt（2002）进一步证实了一步估计要优于两步估计，一步估计又分别对生产无效率的均值和方差与外生变量建立计量回归方程。

（二）生产效率的估计

为了详尽、全面的分析生产无效率方程，本文结合我国旅游业发展的实际情况选取了以下几个代表性的外生变量加入方程：用政府财政占GDP比重来表示政府干预；用当年实际使用外资占GDP比重来表示开放程度；市辖区绿化覆盖率用来表示基础设施建设；用第二、三产业增加值占GDP比重表示产业结构；采用常住人口密度与经济密度表示集聚水平；加入表示东部及西部的区域虚拟变量来考察生产效率的区域差异性。本文实证采用面板数据的SFA模型，分别采用一步极大似然估计（模型1）和两步估计（模型2）进行估计。

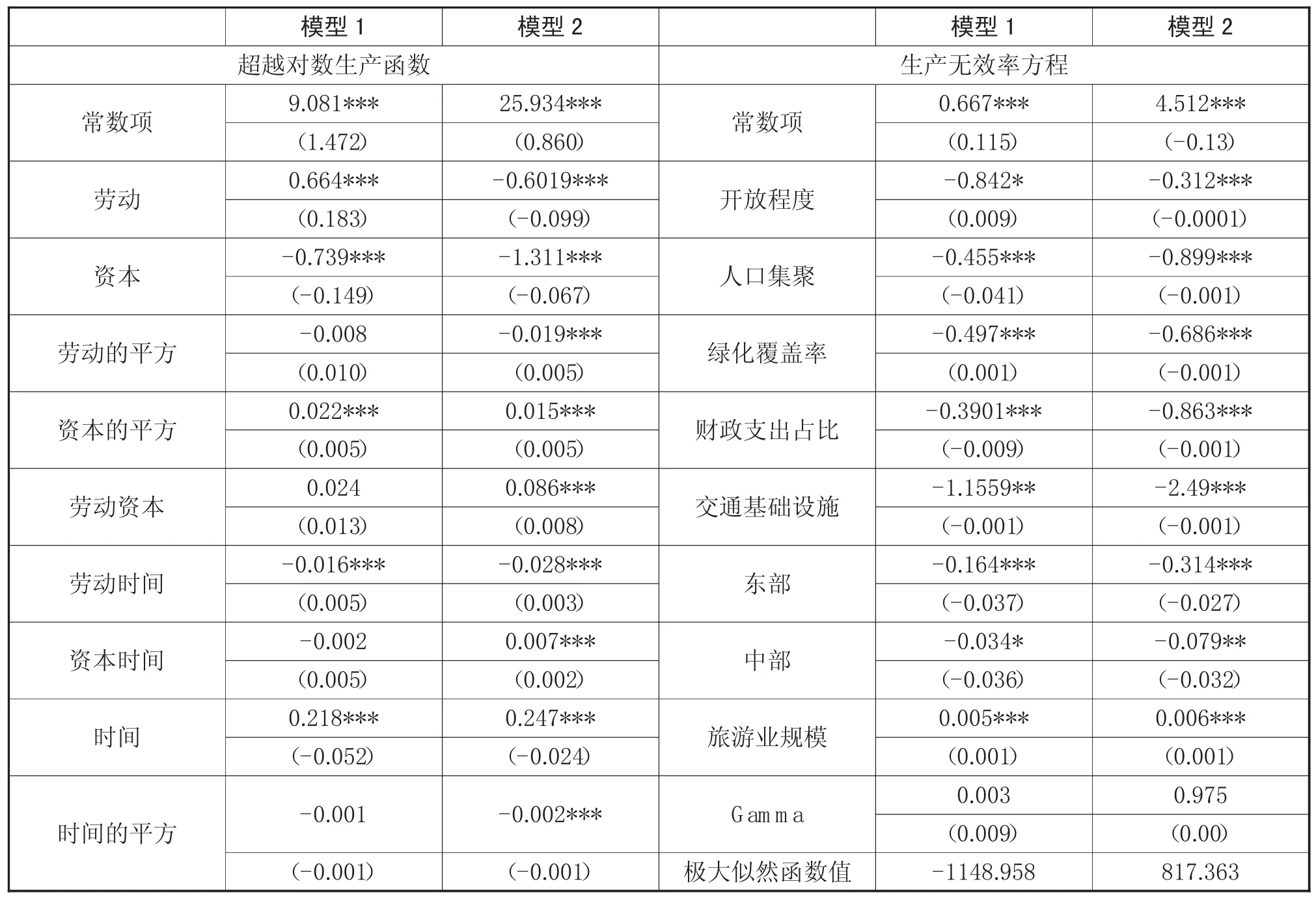
表1 计量回归估计

从以上回归结果来来看，劳动的平均产出弹性为0.563，资本的平均产出弹性为-0.246，比较符合我国旅游业过去的发展模式，过去我国旅游业的增长模式是典型的劳动投入型。在模型2中，gamma系数达到0.975，这表明无效率是生产偏离生产前沿面主要原因。而在模型1中gamma系数很小，仅为0.009，说明在考虑影响生产无效率的外生变量具有较强的解释力。此外，从控制变量对旅游业生产效率的影响情况来看，对外开放程度、人口集聚、绿化覆盖率、交通基础设施、旅游业规模等回归系数均为负，说明对生产效率产生显著的正向影响。从地区虚拟变量来看，东部和中部地区的生产效率显著高于西部地区。

从图2来看，在样本期内，随着时间的推移，生产效率的核密估计曲线逐步偏向左侧，且中值逐步降低，说明我国旅游业生产效率呈现逐步下降的趋势。

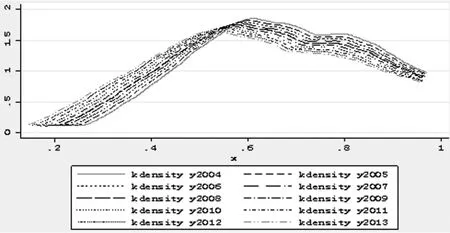
图2各年度生产效率核密度图

我们按各省区域位置进行划分后，发现各地区旅游业的生产效率均呈现随着时间推移不断递减的态势（见图3），这与图2中的情形一致。此外，从图3可以发现，分地区旅游业生产效率呈现较大的差异，东部最高，西部最低，表现出较为严重的空间失衡现象。

③泵送纯水泥浆，水灰比大于0.8，在入口处使用麻絮堵在钢管四周，然后孔内原有清水从另一个孔压出之后，换用水灰比为0.5的水泥浆压入。

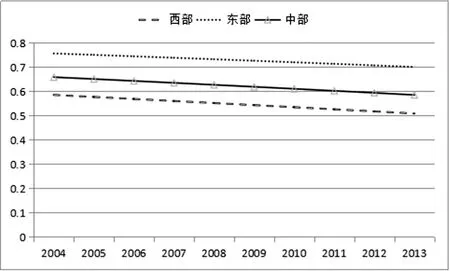
图3各地区生产效率

四、各地区旅游业TFP分解效率及收敛性分析

（一）TFP增长率及其分解效率

本文通过SFA模型估计，本文首先测算出了2005～2013年我国各省区旅游业全要素生产率增长率。并基于Kumbhakar（2000）将TFP分解为技术进步（FTP）、规模效率变化率（SE）以及技术效率变化率（DTE）。

从表2来看，各省区TFP增长率均大于0，为正值，说明各省份旅游业全要素生产率呈现逐年增加的趋势。旅游业全要素生产率增长率最快的为北京（9.21%），最慢的为云南（5.195%）。在旅游业全要素生产率增长率排名前十的省份中，东部地区占5个省份（北京、海南、浙江、广东、福建），中部地区有3个省份（湖北、安徽、黑龙江），西部地区有2个省份（贵州、四川）。排名后十的省份中，东部地区有3个省份（广西、辽宁、天津），中部地区有3个省份（江西、山西、陕西），西部地区有4个省份（重庆、宁夏、内蒙古、云南）。显然，东部地区旅游业的全要素生产率增长率要快于中西部地区。此外，从表2中可以看出，旅游业全要素生产率的增长主要源于技术进步的不断提高，而不是因为规模效率和技术效率的改善。各地区旅游业的规模效率及技术效率变化率甚至为负增长。

从图4可以看出，随着时间的推移，TFP增长率的核密度估计曲线逐步向左移动，且中值呈现逐步降低的趋势，且密度估计值集中度在下降，说明区域间的差异在逐步扩大。

接下来，分区域来看旅游业TFP增长率及其分解效率。

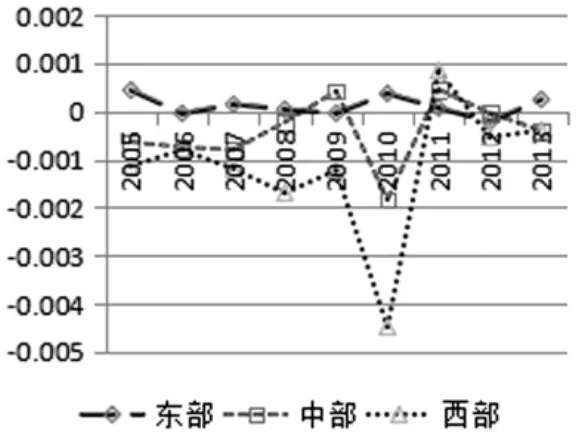
图6各地区旅游业规模效率

图7各地区旅游业技术效率变化率

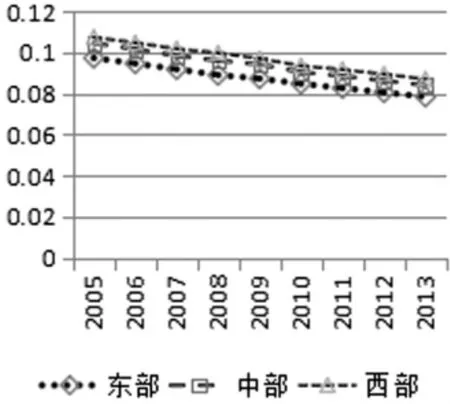
图8各地区旅游业技术进步

从图5可以看出，东、中、西部地区旅游业TFP增长率均呈现逐年降低的趋势，这与图4反映的总体情形一致。此外，分区域旅游业TFP增长率依次递增规律为西部、中部、东部。

从其分解效率来看，由图6可以看出，各地区旅游业规模效率效率的波动性较大。依然呈现出东部最大，西部最小的态势。且仅有东部地区的规模效率呈现递增的趋势。中西部地区基本呈现负的规模效率。总体而言，我国旅游业并未形成明显的规模经济效应。

从图7可以看出，各地区旅游业技术效率变化率呈现逐年递减的趋势，且基本为负增长态势。与TFP增长率一致，依然为东部最高，西部最低。不同于规模效率与技术效率变化率，从图8可以看出，各地区均呈现较为明显的技术进步改进，值得关注的是技术进步增幅也出现连年下降的趋势。此外，分区域的技术进步来看，西部最高，东部较低，而综合观察图5-8，可以看出技术进步是旅游业TFP增长率的主要来源，这也说明，我国旅游业全要素生产率增长率呈现了一定的趋同趋势，但具体的生产效率仍存在较大的差异。

（二）TFP增长率的收敛性分析

对各地区的旅游业TFP增长率进行收敛性分析可以了解在经济集聚约束下各地区旅游业TFP增长率的趋同或发散情况。目前关于收敛性分析的方法主要有三种，分别为：α收敛、绝对β收敛和条件β收敛。本文也从这三种方法出发进行研究。

1、各地区TFP增长率的α收敛性检验

α收敛性检验的内容是不同地区之间TFP的离差随着时间的推移而变化的情况。若离差不断减小，则表示各地区之间TFP的离散程度不断减弱，反之则不断加强。

根据林光平（2006），本文研究的α收敛性检验方程可以写为：

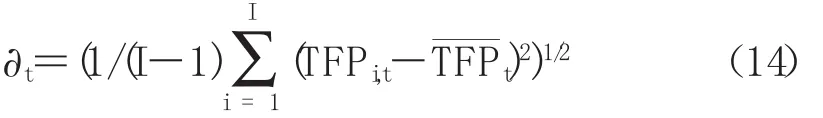
其中，TFPi,t表示在第i个地区在t期的全要素生产率为t时期所有I个地区全要素生产率的平均值。当∂t>∂t+1时，说明存在收敛。

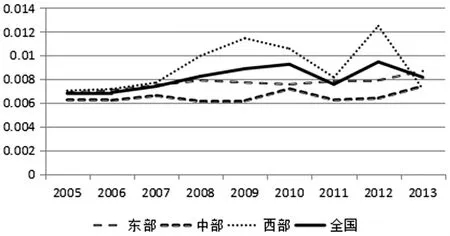
图9 各地区α收敛性检验

从图9的α收敛性检验来看，从2005年到2013年，只有西部地区在波动中呈现收敛趋势，东部和中部地区均未呈现明显的α收敛趋势，从全国层面来看，呈现较为缓和的α收敛趋势，且波动幅度相对稳定。总体而言，区域范围内旅游业的全要素生产率水平仍存在较大的差异，并有逐步扩大的态势。

2、各地区TFP增长率的绝对β收敛检验

绝对β收敛衡量的是不同地区之间TFP增长最终是否可以达到相同的稳定状态，即各个地区的经济发展最终是否存在趋同现象。本文研究全要素生产率的绝对β收敛的表达式如下：

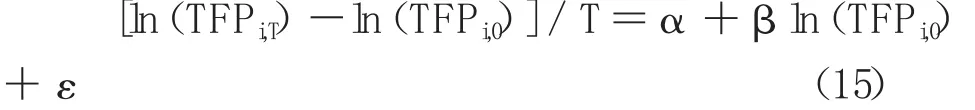
其中，[ln（TFPi,T）－ln（TFPi,0）]／T 表示第 i个地区从从0到T期的年均全要素生产率增长率。A位常数项，ln（TFPi,0）是第i个地区初始时期全要素生产率初始值的对数表达式，β是为变量的系数。若β的回归结果为负值，就说明存在绝对β收敛，即存在落后地区追赶发达地区的现象抑或是趋同现

象。各地区绝对β收敛检验结果如下变所示：

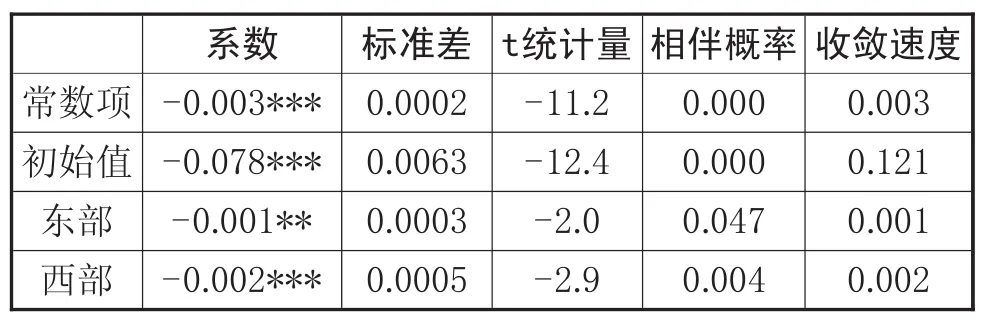
表3 各地区绝对 收敛检验

从以上回归结果来看，全国范围内存在显著的绝对β收敛，收敛速度达12.12%。且虚拟变量皆显著，表明在样本期内，相对落后的地区存在一定的追赶效应，但是收敛速度并不大。结合前面的α收敛检验，可见我国旅游业的TFP增长率并未出现俱乐部收敛现象。

3、各地区TFP增长率的条件β收敛性检验

条件β收敛性检验衡量的是各地区的TFP增长率是否向其稳定水平的收敛。区别于绝对β收敛，条件β收敛允许各地区TFP增长率差异的持续存在。

本文采用Panel Data固定效应模型来检验条件β收敛。其回归方程用以下方式表示：

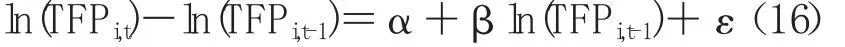
其中，a是固定效应项，β是变量的系数。若β值为负值，就说明存在条件β收敛，即：第i个地区的全要素生产率增长率收敛于其稳定状态。

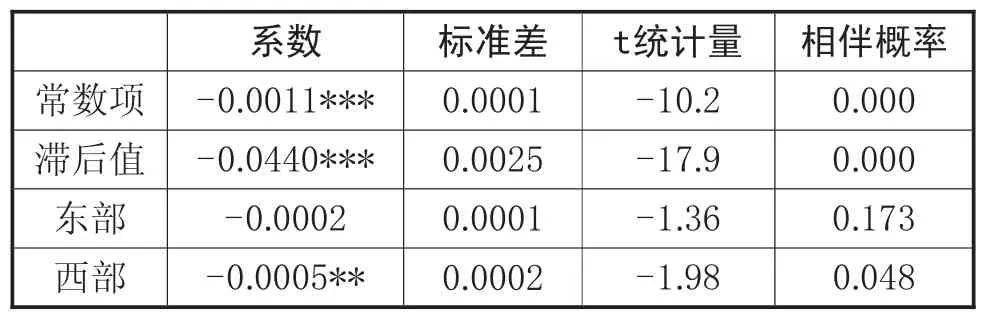
表4 各地区相对 收敛检验

由表4的检验结果可知，东部地区的回归系数虽然为负但不显著，即东部地区不存在条件β收敛，其他地区的回归系数显著为负，说明存在条件β收敛，即旅游业的TFP增长率趋于稳态水平发展。

五、结论及政策建议

本文利用2004年至2013年省级面板数据，通过建立超越对数函数，基于随机前沿方法测算了我国31个省市2005-2013年旅游业的全要素生产率增长率，并对其进行收敛性分析及效率分解，得出以下主要结论：

（1）旅游业生产效率呈现逐年降低的趋势，且东部最高，西部最低，从无效率回归方程的估计结果可以发现，加强对外开放、政府财政支出、交通基础建设、人口集聚等均有利于生产效率的提升，目前我国旅游业生产效率偏离最优前沿主要是由于生产无效率导致，并非是随机误差因素导致。

（2）样本期内，我国旅游业TFP增长率呈现逐步增加的态势，但是增幅在不断减少，各区域间的TFP增长率差异在逐步扩大。其中全要素增长率主要来自于技术进步的提升，而技术效率却为负。从规模效率变动来看，旅游业并未形成可观的规模经济效应。

（3）分区域来看，东、中、西部地区旅游业TFP增长率和技术进步都实现了正增长，而技术效率为负增长，并呈现出“东—中—西”逐年降低的趋势。不同的是，各地区的规模效率呈现波动式变化，其中东部地区的规模效率呈现递增的趋势。中西部地区规模效率变化率为基本为负。

（4）整体而言，全国旅游业TFP增长率存在趋同现象，但并未出现俱乐部收敛现象。各地区存在显著的绝对β收敛，且虚拟变量皆显著，表明在样本期内，相对落后的地区存在一定的追赶效应。东部地区不存在条件β收敛，西部地区存在条件β收敛，即西部地区旅游业的TFP增长率趋于稳态水平发展。

综合上述研究结论，结合我国旅游业出现全要素生产率逐步走低，发展存在空间失衡的现象。本文提出政策建议如下：第一，继续加大旅游业的技术创新力度，创新旅游产品结构和旅游产品体系，不断提升旅游产品的内涵和价值。二是要加强统筹规划力度，不断整合各地区之间旅游资源，走全域旅游发展路线，实现旅游业规模效率外部经济性。三是要注重各区域协同发展，缩小区域经济发展之间的差距。政府要加大对中西部的旅游业投资力度，加强相关基础设施建设。此外。中、西部地区可以向东部地区引进先进技术和人才，学习先进的经营管理制度，加强技术交流合作，实现技术效率的空间溢出效应。

［1］赵磊.中国旅游全要素生产率差异与收敛实证研究.旅游学刊，2013（11）12-23

［2］郭悦，钟廷勇，安烨.产业集聚对旅游业全要素生产率的影响——基于中国旅游业省级面板数据的实证研究.旅游学刊，2015（05）14-22

［3］何俊阳，贺灵.中部地区旅游全要素生产率评价及其影响因素分析.湘潭大学学报（哲学社会科学版），2015（03）85-90

［4］楚尔鸣，马永军.中国全要素生产率增长的区域差异及其收敛性. 区域经济评论，2013（03）59-66

［5］李逸飞，刘楠，李静.基于空间异质视角的TFP分解及其收敛性分析. 金融评论，2014（05）84-93

［6］张丽峰.基于随机前沿分析（SFA）方法的中国旅游业全要素生产率研究.资源开发与市场，2014（02）221-224

［7］张丽峰.基于DEA-Malmquist指数模型的旅游业全要素生产率研究.干旱区资源与环境，2014（07）183-187

［8］ Battese，G.E. and Coelli，T.J. Frontier Production Functions，Technical Efficiency and Panel Data： With Application to paddy famers in India.Journal of Productivity Analysis，1992（3）153-169

［9］ Jondrow，James，C.A.K.Lovell，I.S.Materov，P.Schmidt.On the Estimation of Technical Inefficiency in the Stochastic Frontier Production Function Model.Journal of Econometrics，19，23：8，233-239

［10］Kumbhakar S C，Lovell C A K.Stochastic frontier analysis.New York： Cambridge University Press，2000：216-259

［11］Battese，G.E.and Coelli，T.J.A model for technical effects in a Stochastic Frontier Function for panel data.Empirical Economic，1995（20）325-332

［20］王林聪，中国在中东地区推进“一带一路”建设机遇，挑战及应对，当代世界，2015（9）

［21］李伟建，中国中东外交战略构建研究，阿拉伯世界研究，2016（2）3-16

［22］吴冰冰，中东战略格局失衡与中国的中东战略，外交评论，2013（6）,35-48

［23］王猛，论“一带一路”倡议在中东的实施，现代国际关系，2017（3）16-23

［24］叶淑兰，关于“一带一路”跨文化传播创新的思考，对外传播，2016（4）45-47

［25］国务院新闻办公室网站（http：//www.scio.gov.cn/）