基于正负反馈的SEIR微博舆情传播模型
2018-03-13邱秀连田小虎廖闻剑
邱秀连,田小虎,2,廖闻剑
(1.南京烽火软件科技有限公司,江苏 南京 210019; 2.武汉邮电科学研究院,湖北 武汉 430074)
0 引 言
互联网技术的快速发展,催生了社交网站的迅猛扩张,然而网络舆情相较传统舆情呈现出更迅速、更复杂、更多元,影响也更大的传播特性。
针对社交网络中的网络话题传播问题,网络舆情的传播方式与医学病毒的传播方式有许多相似之处,如文献[1]引入的SIS模型,文献[2]扩展的SIR模型,文献[3]基于SIR模型及群组动力学构建的热点话题传播模型。文献[4]将传染病动力学与复杂网络结合提出了一个基于SNS网络的信息传播模型,文献[5]将潜伏期引入网络舆情传播的带直接免疫的SEIR模型,文献[6]针对舆情话题免疫人员个体记忆的免疫时效性问题的SEIRS模型。
以上模型研究虽然提出了类似传染病动力学模型,但是社交网络中网络水军及僵尸粉这2大特征不容忽视,只有文献微博网络水军识别技术[7]综合了微博水军和最原始的SIR模型,提出了G-SIR模型,但是也未综合针对舆情免疫及僵尸粉这2个特征。
为了解决上述问题,将微博话题传播者中的水军和僵尸粉对话题传播的影响分别作为正反馈和负反馈,再结合传统的舆情传播的传染病动力学模型,更能切合现实网络舆情话题传播的真实热度趋势。
1 基于正负反馈的SEIR微博舆情话题传播模型
1.1 社交网络中的信息传播方式
在社交网络中,舆情信息是以用户为节点,以好友关系为边来传播,类似于传染病从一个节点向另一个节点传播,而用户之间通过关注和粉丝的关系依次扩展,构成一个WS小世界模型,映射真实世界的舆情传播。
1.2 网络舆情话题模型的建立
在SEIR中,系统中的网名处于4种状态(易感态(S)、潜伏态(E)、感染态(I)和免疫态(R)),同时对易感态及潜伏态舆情阵营加入僵尸粉,作为整个模型的负反馈j,对感染态舆情阵营加入水军,作为整个模型的正反馈w。对应到舆情传播系统中,S代表未知者,即未接收到相关舆情信息的网民;E代表已知该舆情信息但犹豫不决,尚未传播该舆情的网民;I代表已得知该舆情信息并已传播该舆情信息的网民;R代表接收到舆情信息,但不感兴趣不会传播的网民。j代表处于潜伏态(E)阵营的网民中的僵尸粉对舆情传播的弱化系数;w代表处于感染态(I)阵营的网民中的水军对舆情传播的增强系数。S(t),E(t),I(t),R(t)分别表示t时刻4类网民占全体网民的数量,模型中S(t),E(t),I(t),R(t)是关于t的连续且可微函数。图1为4类网民之间的状态转移过程。系统中的参数定义及意义如表1所示。
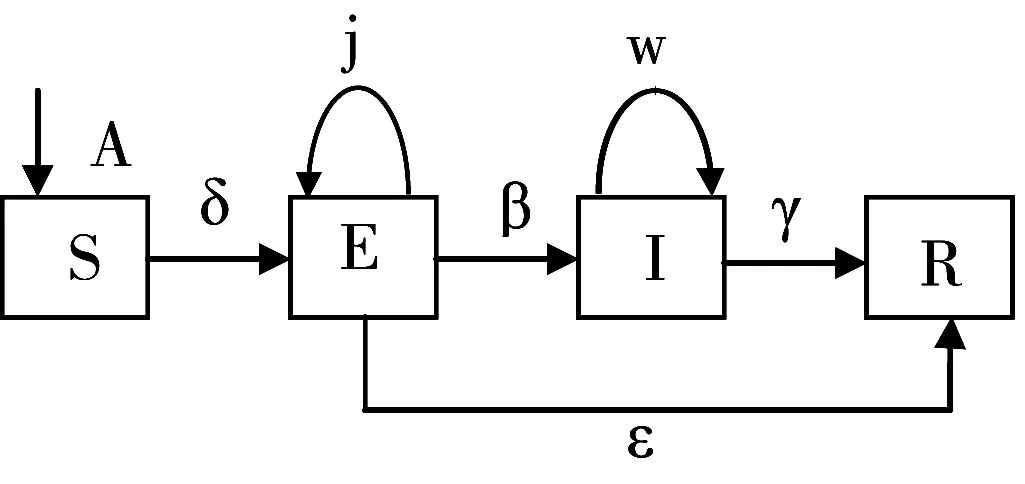
图1 未知者、潜伏者、传播者和免疫者4者转换关系
表1 参数定义及其意义
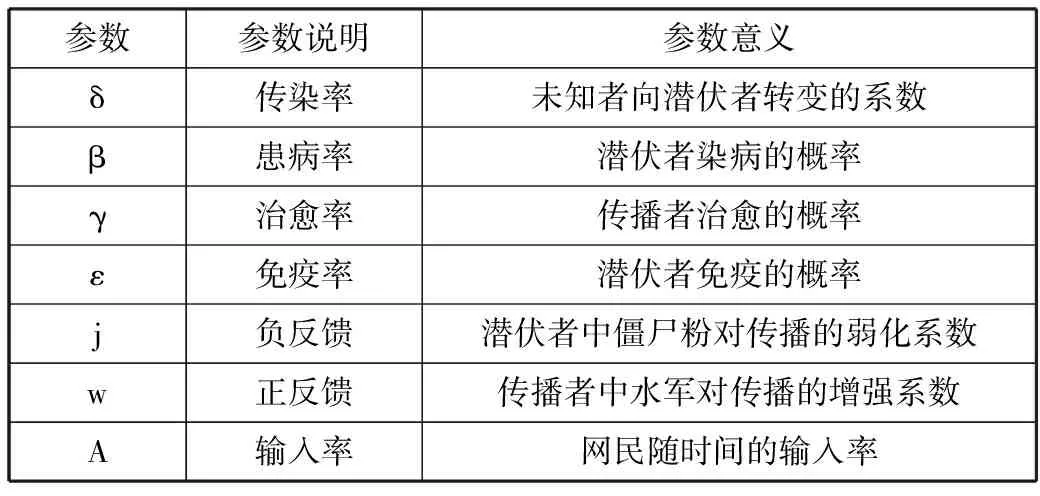
参数参数说明参数意义δ传染率未知者向潜伏者转变的系数β患病率潜伏者染病的概率γ治愈率传播者治愈的概率ε免疫率潜伏者免疫的概率j负反馈潜伏者中僵尸粉对传播的弱化系数w正反馈传播者中水军对传播的增强系数A输入率网民随时间的输入率
显然这些系数都是[0,1]之间的数,且有:
S(t)+E(t)+I(t)+R(t)=1
(1)
根据系统动力学建模思想,建立如下具有正负反馈的SEIR网络舆情传播模型:
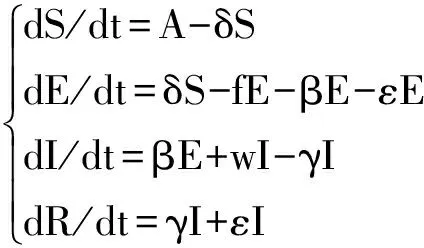
(2)
由于方程(2)前3个方程中均不含有变量R,所以仅考虑由前3个方程所构成的模型即可:

(3)
对方程(3)求积分可得:
(4)
其中C1,C2,C3是常量,做舆情预测时只需要最开始的2个点的参数就可以确定。
舆情热度的增强和减弱可以由传播者阵营的人员流动来直观反映,即:∂I/∂t>0时舆情热度增强,∂I/∂t<0时舆情热度减弱。令方程(3)左边等于零,结合方程(1)可得:
(5)
I*即是系统中的传播转折点,当I>I*时,舆情话题仍将持续增强,当I
舆情传播的热度与各阵营人员流动占比有直接关系,当潜伏者和传播者占比高时舆情热度高,舆情的走向则与未知者和免疫者有关,最初未知者人员占比高时,舆情呈扩大传播态势,当最终免疫者人员占比高时,舆情呈热度衰减态势。此外,网络舆情传播过程中,各个阵营都有可能存在僵尸粉或水军,但是只有该舆情话题相关的潜伏者中的僵尸粉,一定比例上直接弱化传播热度,构成负反馈;也只有该舆情话题相关的传播者中的水军,对舆情话题的推波助澜,一定比例上直接强化话题传播,构成正反馈。当两者在其他阵营时并未直接影响话题热度。
2 试验仿真
2.1 数据来源
本文采用新浪微博数据集,为避开新浪反爬虫机制,采用模拟手机端登录进行数据采集,数据从某一微博用户出发,抓取该用户的个人信息、关注列表、历史微博,然后根据关注列表依次循环抓取以上信息,最后构成的网络符合WS小世界模型。此处需说明新浪微博关注只能查看前200人,根据抓取到的结果,具体分析2016年底某乔姓明星抑郁自杀事件,抓取到的微博中涉及该事件的博文5026条,话题传播者1163人,扩展出这1163人的粉丝7873人、关注9751人。分析该网络的拓扑特征可知,该网络的平均出度为8.38,说明每个节点大约有8个关注对象,最大出度为430,说明某些节点多达430个关注对象;最大入度为65,说明某些节点最大有65个粉丝。
试验中的水军,对相应文本切词后,与已训练好的样本利用综合指数和熵值法实现水军的自动判别;试验中的僵尸粉,根据用户的个人信息、博文信息实现基于贝叶斯模型的僵尸粉自动判别。
2.2 试验结果及分析
2.2.1 不同节点的密度随时间的变化关系
1163人的原始博文信息中提及乔姓明星最早的时间是2010-08-05 12:20:12,但相关话题急剧增长是在2016-09-16日,因此从该急剧增长点前5天2016-09-11 00:00:00日开始统计相关信息。最早时间为2016-09-14 17:12:42由微博ID为2047549550的博主发布的一条信息,设初始网络仅有一个传播者,其他全部为未知者,将方程(2)中的各参数设置如下:传染率δ=0.3,患病率β=0.2,治愈率γ=0.4,免疫率ε=0.3,正反馈w=0.2,负反馈j=0.1。网络舆情传播过程中各舆论阵营及总体舆情衍化态势如图2所示。每日网民输入率A已知时,模型预测热度及实际网络传播热度(以计算传播者I直观反映)如图3所示。

图2 舆情传播总体衍化
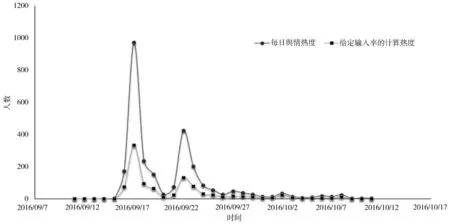
图3 每日舆情热度与预测热度
2.2.2 微博水军及僵尸粉对舆情衍化的影响
对舆论个体中的每个对象,利用综合指数和熵值法水军自动判别模型和贝叶斯僵尸粉自动判别模型,判别舆情衍生过程中潜伏者阵营中的僵尸粉和传播者阵营中的水军。判别情况如图4所示,数量参考右边次坐标轴。将僵尸粉和水军加入舆情衍生模型中,僵尸粉和水军对舆情热度的影响如图4所示,数量参考左边主坐标轴。
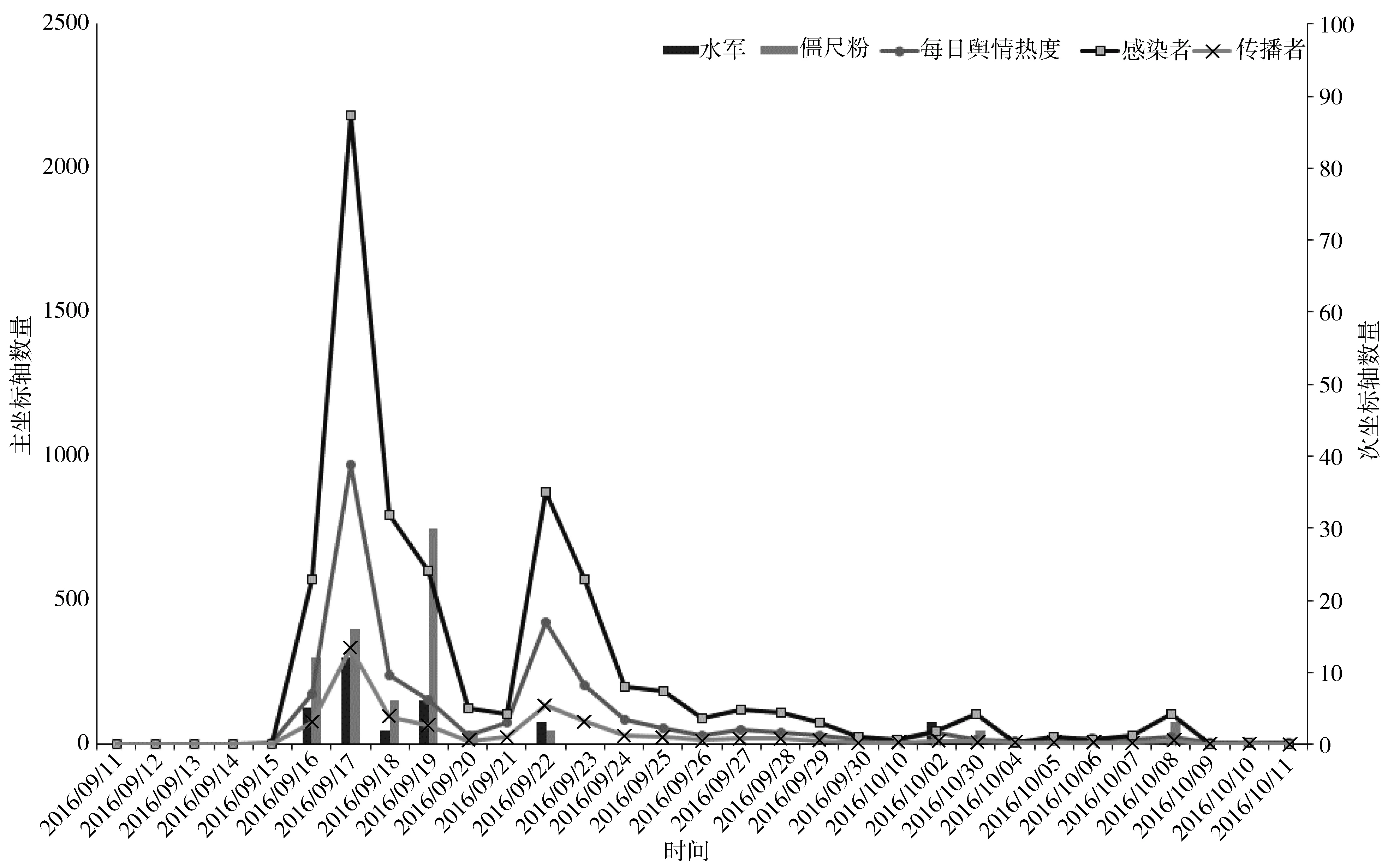
图4 加入水军和僵尸粉的舆论个各阵营衍化态势
表2 感染者、传播者与每日舆情的相关性
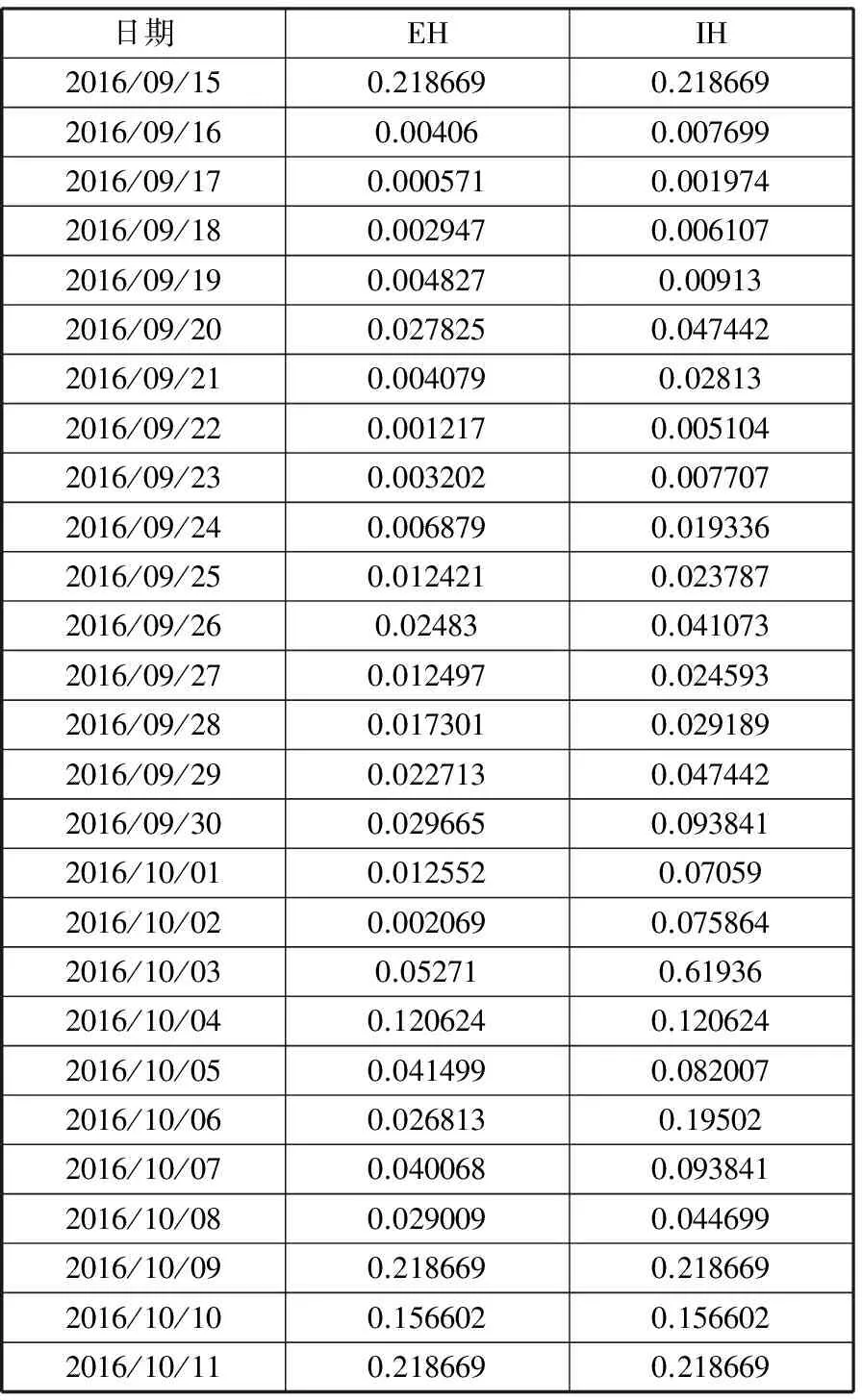
日期EHIH2016/09/150.2186690.2186692016/09/160.004060.0076992016/09/170.0005710.0019742016/09/180.0029470.0061072016/09/190.0048270.009132016/09/200.0278250.0474422016/09/210.0040790.028132016/09/220.0012170.0051042016/09/230.0032020.0077072016/09/240.0068790.0193362016/09/250.0124210.0237872016/09/260.024830.0410732016/09/270.0124970.0245932016/09/280.0173010.0291892016/09/290.0227130.0474422016/09/300.0296650.0938412016/10/010.0125520.070592016/10/020.0020690.0758642016/10/030.052710.619362016/10/040.1206240.1206242016/10/050.0414990.0820072016/10/060.0268130.195022016/10/070.0400680.0938412016/10/080.0290090.0446992016/10/090.2186690.2186692016/10/100.1566020.1566022016/10/110.2186690.218669
舆情传播中感染者阵营中的僵尸粉对舆情演化起负反馈,传播者阵营中的水军对舆情演化起正反馈,因此有僵尸粉和水军存在的情况下,感染者和传播者对每日舆情热度都有不同的影响。表2分别计算了感染者和传播者与每日舆情热度的余弦相似度作为相关性。EH是感染者阵营与每日舆情热度的相关性,IH是传播者阵营与每日舆情的相关性。
根据表2中的相关性系数,结合图中的实际情况,9月15号、9月20、10月4号、10月9号EH和IH基本是最大的几个值,是影响曲线的极大值点。结合图4实际舆情衍化态势9月16号、9月19号感染者或传播者中有水军和僵尸粉,10月3号、10月8号感染者中有僵尸粉,因为后一天出现较大变化因此余弦相似度即相关性才会变大。另外,虽然9月17号、9月18号、9月22号有僵尸粉或水军的出现,但是本身感染者或传播者阵营的人员都很大,因此僵尸粉或水军的影响系数并不大,这样成功地过滤了因为感染者或传播者群体数过大造成僵尸粉或水军增加的影响,真实地反映了负反馈系数j和正反馈系数w的影响。
本文分析了真实舆情网络中僵尸粉和水军对舆情传播的影响因素。舆情传播中遇到僵尸粉时,虽然舆情感染者基数增加但是舆情热度并未增加;另一方面,当舆情传播中遇到水军时,虽然感染者基数并未增加,但是舆情热度大大增加。以上2种情况在以往的传染病分析模型中,都没有考虑到是直接以固定传染率和患病率来计算,因此结果有较大出入。
3 结束语
本文以传染病动力学模型中的SEIR为基础,通过引入新的群体:僵尸粉和水军,构建了微博舆情话题传播模型。分析加入正负反馈的SEIR模型中宏观舆情演化态势和正负反馈的影响。仿真结果表明:1)网络舆情突发事件中从衍化热点到冷淡的整个周期中,僵尸粉和网络水军的参与已经成为影响舆情热度的常态化现象和不容忽视的重要因素;2)僵尸粉对传统舆情的分析模型带来极大误判,而水军对真实的舆情热度炒作更是重中之重;3)僵尸粉对舆情热度产生抑制作用,水军则会对舆情热度产生推动作用;4)本文的构建模型只是简单的开始。更加精确的僵尸粉和水军的判定、更加精准的相关性和热度分析、更加多维的网络舆情阵地的模型校正将是今后研究的重要内容。
[1] Migram S. The small-world problem[J]. Psychology Today, 1967(2):60-67.
[2] Leskovec J, Mcglohon M, Faloutsos C, et al. Patterns of cascading behavior in large blog graphs[C]// Proceedings of the 7th SIAM International Conference on Data Mining. 2007,7:551-556.
[3] Gruhl D, Guha R, Liben-No well D, et al. Information diffusion through blog space[C]// Proceedings of the 13th International Conference on World Wide Web. 2004:491-501.
[4] 张彦超,刘云,张海峰,等. 基于在线社交网络的信息传播模型[J]. 物理学报, 201160(5):60-66.
[5] 陈波,于泠,刘君亭,等. 泛在媒体环境下的网络舆情传播控制模型[J]. 系统工程理论与实践, 2011,31(11):2140-2150.
[6] 陈福集,陈婷. 基于SEIRS传播模型的网络舆情衍生效应研究[J]. 情报杂志, 2014(2):108-113.
[7] 程晓涛. 微博网络水军识别技术研究[D]. 郑州:中国人民解放军信息工程大学, 2015.
[8] 丁学君. 基于SCIR的微博舆情话题传播模型研究[J]. 计算机工程与应用, 2015,51(8):20-26.
[9] 林晓静,庄亚明,孙莉玲. 具有饱和接触率的SEIR网络舆情传播模型研究[J]. 情报杂志, 2015(3):150-155.
[10] 谭娟. 基于传染病模型的社交网络舆情话题传播[J]. 计算机工程与应用, 2015,51(12):118-122.
[11] 陈福集,陈婷,郑小雪. 一类新SEIRS模型上的网络舆情传播行为研究[J]. 情报资料工作, 2014(4):35-36.
[12] 张艳梅,黄莹莹,甘世杰,等. 基于贝叶斯模型的微博网络水军识别算法研究[J]. 通信学报, 2017,38(1):44-53.
[13] 袁旭萍,王仁武,翟伯荫. 基于综合指数和熵值法的微博水军自动识别[J]. 情报杂志, 2014(7):176-179.
[14] 王越,张剑金,刘芳芳. 一种多特征微博僵尸粉检测方法与实现[J]. 中国科技论文, 2014(1):81-86.
[15] 王越,张剑金. 一种应用SAVBP神经网络的僵尸粉判别方法[J]. 重庆理工大学学报, 2014,28(4):72-76.
[16] Fan Meng, Li M Y, Wang Ke. Global stability of an SEIS epidemic model with recruitment and a varying total population size[J]. Mathematical Biosciences, 2011,170(2):199-208.
[17] Zhang Beibei, Guan Xiaohong, Khan M J, et al. A time-varying propagation model of hot topic on BBS sites and Blog networks[J]. Information Sciences, 2012,187(1):15-32.
