海洋绞车提升系统动力学仿真分析*

黄良沛， 陈 磊， 邹东升

(1.湖南科技大学 机械设备健康维护省重点实验室，湖南 湘潭 411201; 2. 湖南科技大学 机电工程学院，湖南 湘潭 411201)

0 引 言

21世纪人类将全面进入海洋经济时代，开发利用海洋资源，发展海洋经济已成为各国的长期战略决策[1]。我国在海洋资源装备技术开发方面起步比较晚，由于受到各种技术的限制，目前我国的海洋船用绞车主要依靠进口，我国自主的海洋绞车研究尚处于起步阶段。随着对深海的开发，对于拥有自主知识产权的海洋绞车显得越来越重要。

总体来说，由于海洋绞车作业时外界因素干扰太大，并且单纯的通过实验来获取绞车吊放物体的运动特征难以实现并且成本太高，周期太长，所以在现阶段，用虚拟样机技术对海洋绞车的传动系统进行动态的仿真分析是非常有必要的，因此，笔者尝试建立海洋绞车的虚拟样机模型，并分析绞车在提升过程中速度、加速度和拖动力的变化规律。考虑到绞车在作业过程中，由于波浪激励的影响，缆绳张力会出现大幅度振动，使得缆绳可能因受到频繁的冲击载荷而失效断裂[2-4]。所以笔者还分析了母船在受到波浪激励时负载的动态响应以及缆绳的张力变化规律，为海洋绞车近一步进行升沉补偿研究提供理论依据。

1 海洋绞车提升系统动力学计算

1.1 海洋绞车运动规律

目前提升设备比较典型的速度图为六阶段速度图、五阶段速度图以及三阶段速度图。考虑到海洋绞车的特殊工况以及卷筒容绳量大、缠绕层数多等特点，所以将海洋绞车的提升过程划分为10个阶段。如图1所示。

图1 海洋绞车提升速度图

1.2 提升系统变位质量

在提升机动力学方程中，需计算各运动部分的惯性力，而系统中的部件存在直线和旋转两种运动形式，使得计算总惯性力时很不方便，在建立其动力学方程时，可以用一个假想的集中在卷筒圆周表面的当量质量来代替提升系统所有运动部分的质量，如表1所列。

表1 海洋绞车各阶段提升时间、加速度以及提升高度

称为变位质量[5]，以∑m表示。变位原则是变位前后动能不发生变化，以电动机转子的变位质量为例：设Jd′为电动机转子的转动惯量，Jd为变位到卷筒圆周上的转动惯量，设ω′为电动机的角速度，ω为卷筒角速度。根据变位前后动能相等的原则，应当有如下关系：

(1)

(2)

式中：i为减速器的传动比。

所以电动机转子变位到卷筒圆周上的质量md为：

(3)

式中：R为卷筒缠绕半径。

其它各部件变为质量的计算大致相同，在此不多做赘述。

1.3 提升系统动力学方程

海洋绞车提升系统动力学方程为：

F=kmg+mpg(H-x)+∑ma

(4)

式中：F为电动机提供的拖动力，N ；k为海水阻力系数，k=0.55～88；m为提升重物质量，kg；∑m为变位质量，kg；mp为提升缆绳每米质量，2.5～2.7 kg/m；h为缆绳下放深度，h=H-x，m；H为水面至水下作业位置的高度，m；x为提升重物离开水下作业位置高度。

2 海洋绞车虚拟样机模型的建立

图2给出了海洋绞车的整体结构示意图，此外，在整个系统中还包含大量的垫片、螺栓等零件，在进行动力学仿真时，这些零件存在与否对于仿真结果几乎没有影响，所以为了提高工作效率，在建立传动系统的虚拟样机模型时选择用布尔运算对这些零件求和或者忽略这些零件。

图2 海洋绞车整体结构示意图 1.卷筒编码器 2.缆绳 3.绞车卷筒 4.卷筒驱动电机组5.丝杠编码器 6.丝杠 7.导缆轮 8、9.行程开关 10.交流伺服电机 11.减速器 12.转盘轴承

2.1 建立零部件的三维几何模型

因为在ADAMS软件建立几何模型不方便，所以选择在UG中建立绞车各个部件的三维实体模型并完成装配，在完成装配后再利用UG自带的motion模块为各个部件添加相应的约束副，最后导出ADM文件，系统会自动生成后缀名为.adm /.xmt_txt/.cmd的三个文件，在ADAMS中依次导入前两个文件，建立除绳索以外的虚拟样机模型。

2.2 建立钢丝绳模型

综合考虑了多种有关钢丝绳建模的方法[5-8]，之后结合具体需求，决定采用ADAMS二次开发宏命令来建立钢丝绳模型，由于设计之初绞车的绳索总共长达4 000 m，为了减小计算工作量，以及保证模型的可靠性，取1 000段离散化小钢丝绳进行模拟，每段钢丝绳长100 mm，将多余绳索的质量折合到负载上,最终虚拟样机模型如图3所示。

图3 绞车虚拟样机模型

2.3 确定轴套力、接触力参数以及驱动函数

2.3.1确定轴套力参数

(5)

式中:K11为拉伸刚度系数；K22、K33为剪切刚度系数；K44为扭转刚度系数；K55、K66为弯曲刚度系数E、G分别为钢丝绳弹性模量与横截面积；A、D、L分别为钢丝绳的横截面积、直径和每段小圆柱的长度；I为钢丝绳横截面对中性轴的惯性矩。

对于阻尼系数目前没有确定的计算公式，一般取对应刚度系数的2%。

2.3.2确定接触力参数

海洋绞车在作业过程中，钢丝绳会与滚筒、导线轮以及导线柱之间发生接触碰撞，为了使模型尽可能接近真实情况，电机齿轮与滚筒齿轮之间放弃使用齿轮副改为接触[9-10]。在ADAMS中设置接触力时一般需要刚度系数、碰撞指数、阻尼系数以及切入深度四个参数。

其中，刚度系数为:

(6)

式中:1/R=1/R1+1/R2；R1、R2为两个相接触物体的半径。

E*与物体弹性模量以及泊松比关系如下：

(7)

式中:E1E2为相接触物体的弹性模量；V1V2为相接触物体的泊松比。

金属与金属之间碰撞指数一般取1.5；最大阻尼系数通常设定为刚度系数的0.1%～1%，切入深度：文中取默认值0.1。

2.4 波浪激励模型

在受到波浪的影响时，绞车整体会随着母船做升沉运动，此时各个部件尤其是钢丝绳内部的张力会发生较大变化，为了研究这一变化规律，在进行仿真研究时，文中对绞车整体施加一个激励，来模拟船体的升沉运动，再根据表1编写电机的驱动函数以控制电机的转速[11]，从而实现绞车在提升过程中的升沉补偿。现假设波浪为简单的正弦波，波浪周期为T，高度为H，船体的位移与波浪高度的比值为μ，μ取值一般小于0.5，船体的运动周期与波浪周期T相同[12]，则船体的升沉位移可描述为[13]：

在铁路工程连续梁桥的施工控制中，自适应控制方法也是铁路工程连续桥梁施工控制中的重要方法之一。该方法在现阶段铁路工程连续桥梁施工中的应用是最为普遍的，主要是对计算参数进行分析，将分析后的参数结果与实际参数加以对比，了解参数偏差。在此基础上，对参数进行估计与修正，将修正和识别后的参数，应用到下阶段的实时结构分析与往复循环中。经过多个铁路工程连续桥梁的施工阶段，得到的参数取值会最大限度地趋于合理，且软件模拟计算结果也会与铁路工程连续桥梁施工的实际情况相适应。一般来说，连续桥梁的自适应控制法多应用于大跨度结构的连续桥梁施工中，且是在闭环控制方法基础上展开的。

(8)

现设定的海况为四级，对应波高H的有效值为[1.25 m 2.5 m]，周期为[4.7 s 5.8 s]，取H为2 m，T为5 s，μ为0.5 s，则有：

(9)

3 仿真结果分析

由于整个提升过程持续时间太长，并且不需要对整个提升过程做完整的仿真分析，笔者主要针对以下几个特殊阶段进行仿真：①从启动到第一个主匀速阶段(t0～t2)，设置仿真时间为8 s，Steps为400；②由第二个主匀速阶段末加速至第三个主匀速阶段(t4～t6)，设置仿真时间为12 s，Steps为600；③负载从最大速度开始减速直到绞车停止作业(t6～t9)，设置仿真时间为24.2 s，Steps为1 210。

3.1 负载提升速度分析

各阶段提升速度随时间变化关系如图4～6。

图4 t0～t2阶段负载的提升速度与母船速度曲线

前2 s钢丝绳处于预紧阶段，所以负载的提升速度为0，于2.0 s左右负载开始加速上升，4.5 s后加速完毕，速度逐渐趋于稳定，维持在1.0 m/s左右。由于钢丝绳具有较大的弹性，当加速度突然发生变化时会产生较大振动，所以速度变化曲线并不平稳。从2.0 s开始，绞车受到母船升沉运动的影响，负载的提升速度与原先相比出现较大幅度的波动，就整体而言，负载提升速度的变化规律与母船运动规律接近，不过由于此时钢丝绳弹性刚度较小，钢丝绳的伸长量较大，负载提升速度曲线与母船运动规律不完全一致。

图5为t4～t6阶段负载提升速度和母船运动速度随时间的变化关系。为了对该阶段进行仿真，通过控制电机转速使得负载的提升速度在较短的时间内达到1.2 m/s，进入主匀速阶段(t4)，之后匀速运行,并在7.0 s时进入主加速阶段(t5)，经过0.47 s的短暂加速，负载提升速度达到最大值1.67 m/s，进入主匀速阶段(t6)，之后电机匀速运行，直至仿真结束。

图5 t4～t6阶段负载的提升速度与母船速度曲线

图6为t7～t9阶段负载提升速度和母船运动速度随时间的变化关系。从1.0 s开始，进入主减速阶段(t7)，此时负载的提升速度为1.67 m/s，减速时长为1.17 s，负载的提升速度下降至0.5 m/s，之后负载进入长达20 s的匀速上升阶段，在t=22.17 s时，绞车盘刹开始工作，1 s后绞车停止。

图6 t7～t9阶段负载的提升速度与母船速度曲线

从4.0 s开始绞车受到波浪激励影响。由于此时负载已经接近海面，钢丝绳长度只有10 m左右，弹性刚度系数较大，所以负载的速度变化规律与母船的升沉运动变化规律非常接近，在t=4.0 s时负载提升速度有一个突变过程，经过短暂波动后迅速稳定。

3.2 滚筒拖动力分析

各阶段中滚筒与钢丝绳铰接处受力随时间变化关系，如图7～9所示，由于绞车传动系统较为复杂，所以在综合考虑到钢丝绳质量与弹性的情况下，暂时无法建立一个准确的数学模型来描述系统拖动力的变化规律，在公式(4)中，忽略了钢丝绳的弹性刚度，对于系统突然加减速时滚筒拖动力的计算不够准确，与仿真值有较大的差距，但是在系统趋于平稳后，钢丝绳形变量极小，公式(4)对于拖动力的计算值与仿真值比较误差较小。

图7 t0～t2 阶段滚筒拖动力

图7中0～4 s为初始加速阶段，可以很明显的看出在0～3 s过程中拖动力曲线波动较大，而在3～4 s时，系统趋于稳定。表2中列出了各个阶段滚筒拖动力的仿真结果与理论值，仿真结果取平均值，记为F*。其中t0阶段中钢丝绳预紧时间不算在内。由于t1阶段持续时间非常短，并且由于钢丝绳的能起到一定的缓冲作用，所以仿真结果与理论值相差较大。

表2 t0～t2 阶段滚筒拖动力

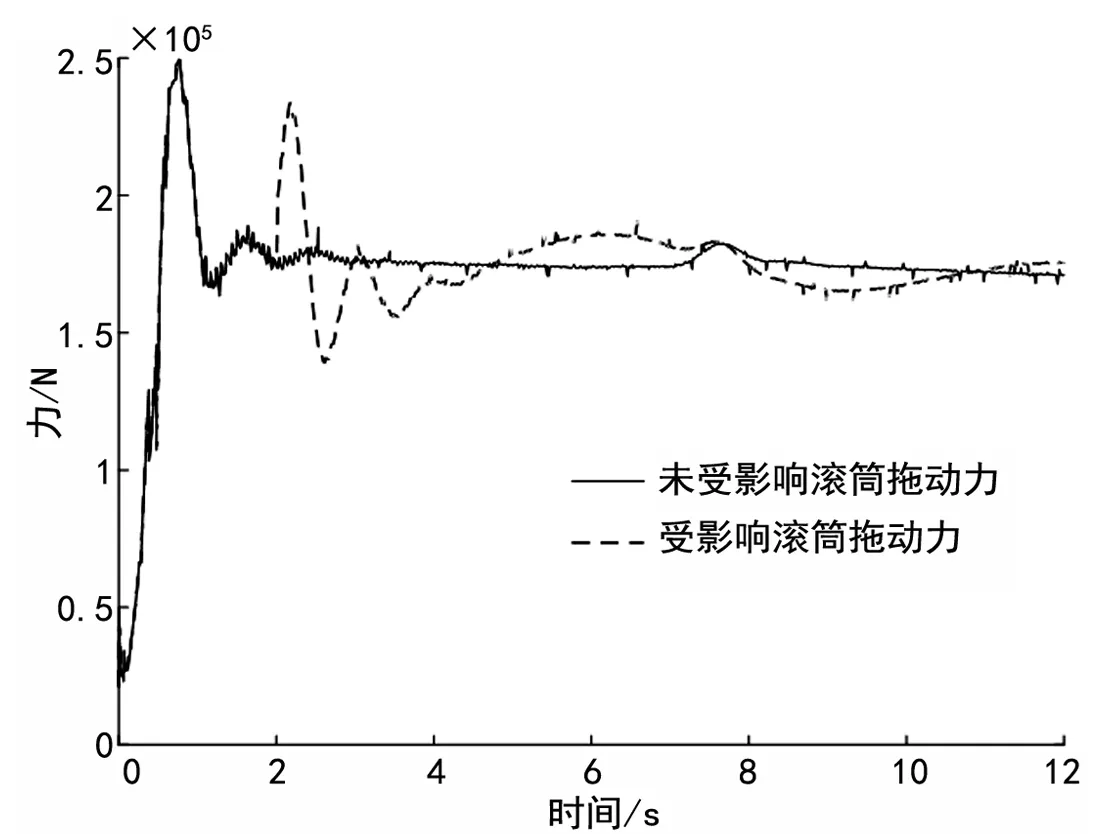
图8 t4～t6阶段滚筒拖动力

表3给出了t4～t6阶段滚筒的拖动力，7.0 s时负载进入加速阶段(t5)，加速时间只有0.47 s，与t1阶段一样仿真值与理论值相差较大，在但是在t4与t6阶段仿真值与理论值都非常接近。

从1.0 s时开始，负载进入主减速阶段(t7)，此时滚筒拖动力波动非常大，直到2.17 s开始停止减速，负载匀速上升，此时拖动力一直在113 365.1 N上下小幅度波动，此阶段拖动力的理论值为111 134.8 N，误差为1.75%。

从图8～9的仿真结果来看，当负载匀速上升时，理论值与仿真结果相差较小。当负载突然加速或减速时，由于公式(4)中并未考虑到钢丝绳的弹性，仿真结果与理论值出现较大误差。

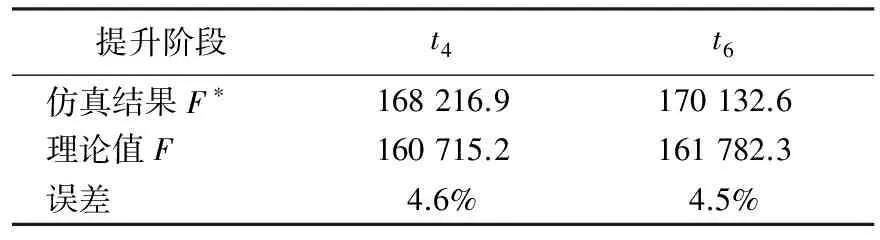
表3 t4～t6 阶段滚筒拖动力

图9 t7～t9 阶段滚筒拖动力

从仿真结果可以看出，当海洋绞车受到船舶运动影响时，滚筒拖动力会突然变化，最大时能够达到8 000 N左右，钢丝绳会受到更大的冲击变载荷，传动系统的可靠性与稳定性也会随之受到影响。

4 结 论

利用UG精确建立了海洋绞车的三维结构模型，

之后利用ADAMS完成了虚拟样机模型的建立，并对绞车的提升过程进行仿真分析，发现在系统在突然加减速时理论计算值并不能很好的反应卷筒的拖动力，但在系统趋于稳定的状况下，二者得出的结果非常接近，速度曲线与理论值非常吻合，说明虚拟样机模型较为合理。之后分析了母船的升沉运动对负载运动的影响，获得了在波浪激励的影响下负载的动态响应及钢丝绳的张力变化，以此为基础可以预测海洋绞车进行升沉补偿或恒张力控制时电机所需转速。从仿真结果可以看出母船的升沉运动对与负载的运动、滚筒的拖动力以及缆绳的张力都有较大的影响，在设计传动系统选取关键零部件时，必须要考虑到这些因素。

[1] 曹忠祥.我国海洋战略资源开发现状及利用前景[J].中国经贸导刊,2012(6):38-39.

[2] Rahul S. Deep sea mining economic, technical, technological, and environmental considerations for sustainable development[J].Marine Technology Society Journal,2011,5(5):28-41.

[3] 刘德顺，金永平，万步炎，等.深海矿产资源岩芯探测取样技术与装备发展历程与趋势 [J].中国机械工程,2014,25(23)：3255-3265.

[4] Yongping Jin, BuyanWan. Dynamic analysis of launch & recovery system of seafloor drill under irregular waves[J].Ocean Engineeriing,2016(117): 321-331.

[5] 董未来，陈尤龙.提升系统总变位质量的分析及测定[J].煤矿机电,2010(1):62-63.

[6] 黄祥声，曾钦达.基于ADAMS的门座起重机钢丝绳动力学仿真[J].起重运输机械, 2012(7):109-112.

[7] Andrew S E. Efficient modeling of extensible cables and pulley systems in adams[C]. In:Europe Adams Conference,London,2002:1-10.

[8] 李智伟,杨永发.基于ADAMS_Cable的烟草打顶机钢丝绳升降系统的动力学仿真[J].林业机械与木工设备,15(6):28-06.

[9] 洪青泉，程 颖.一种齿轮副模型及其在多体动力学仿真中的应用[J].兵工学报,2003,24(4):509-512.

[10] Astoul J, Mermoz E, Sartor M, et al. New methodology to reduce the transmission error of the spiral bevel gears[J].CIRP An-nals-Manufacturing Technology,2014,63(1):165-168.

[11] Mechanical Dynamic Inc. ADAMS/solver user’s guide[M].[s.l]:Mechnical Dynamics Inc.,2002.

[12] 姜 浩.半主动式钻井绞车升沉补偿系统[J].机床与液压,2012,40(1):85-88.

[13] 杨建民，肖龙飞，盛振邦.海洋工程水动力学试验研究[M].上海:上海交通大学出版社,2008.