摩擦传动的压电定位台高精度跟踪控制

严刚峰 方 红 谭健敏 罗浚溢

(成都大学信息科学与工程学院， 成都 610106)

0 引言

近年来，随着科技的迅速发展，在光学工程、精密机械制造、精密仪器仪表、集成电路制造、航空航天工业、机器人等高新技术领域，迫切需要微米级的驱动和定位跟踪技术，传统的电磁电机已很难在高精度上满足需求，压电执行器作为压电致动装置的一个分支，是利用压电元器件的逆压电效应，将压电元器件的往复运动转换为弹性元件的微小运动，并通过摩擦力的作用将弹性元件的微小运动转换成动子宏观的运动，其结构非常紧凑、转子惯性较小、响应制动很快、可直接驱动负载，具有低速和高转矩的特性。而传统电磁电机虽然转速较高，但是转矩较小，且易受环境电磁场的影响。压电执行装置不仅没有电磁场，而且还具有良好的定位以及速度的可控性。选用压电执行装置作为执行元件，设计合理的控制策略来实现高精度的驱动控制具有重要意义。

关于压电执行器的研究主要集中在压电电动机的结构研究及其驱动电路设计[1-5]，最大行程仅为几微米的压电执行器控制方法研究[6-14]，以及压电材料的性能分析及其实验研究[15-18]。对于具有大行程的压电工作台的高精度跟踪控制方法的研究则报道很少。本文首先针对选用的摩擦传动压电定位台，根据其工作原理，建立摩擦传动的压电定位台控制系统的时域数学模型，然后根据该模型，设计一种加模型补偿的滑模变结构控制策略。

1 摩擦传动压电定位台控制系统建模

1.1 摩擦传动的压电定位台控制系统

选用如图1所示摩擦传动的压电定位台控制系统，压电电动机、电机驱动器及其电源、摩擦传动工作台都选用PBA Systems公司的PLS8-115型压电定位台系统。

图1 摩擦传动的压电定位台控制系统Fig.1 Piezoelectric positioning control system with friction-driven1.电机驱动器 2.电源 3.编码器 4.压电电机 5.工作平台

该定位台系统工作原理是利用压电陶瓷的逆压电效应，原理示意图如图2所示，在给摩擦传动的压电定位台输入驱动电压之后，压电电动机中的压电陶瓷就会产生逆压电现象，产生的纵向延伸和横向弯曲的形变，在陶瓷指尖所在的狭小椭圆通道里产生超声驻波，挤压驱动带的陶瓷指尖就会产生如图2所示运动方向的驱动力，通过压电电动机内部的驱动电路控制2个陶瓷指尖产生高频的交替振动，由交替振动的陶瓷指尖和驱动带之间的摩擦力来驱动固定在驱动带上的工作平台作如图2所示方向的直线运动。在没有驱动电压输入时，陶瓷指尖对驱动带的压力可在工作平台上维持一个保持力矩，不产生移动。

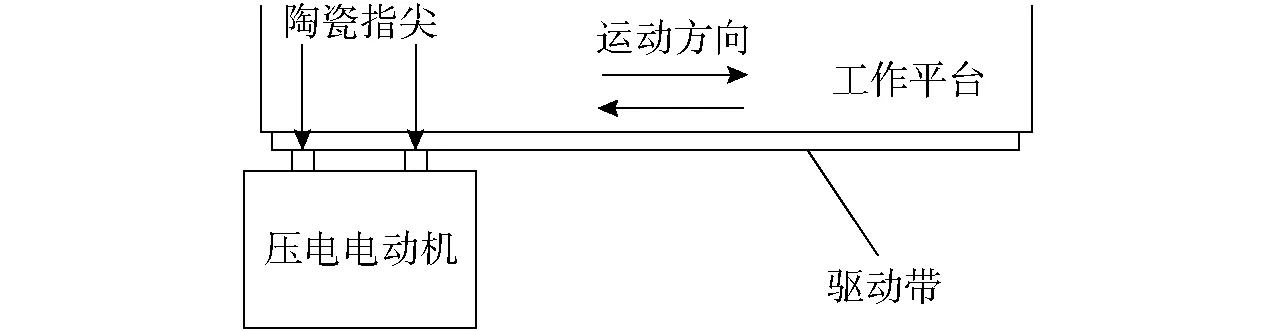
图2 压电电动机定位台工作原理示意图Fig.2 Operation principle diagrammatic sketch of piezoelectric motor positioning stage

1.2 摩擦力类型

压电电动机系统中主要存在的摩擦力类型有静摩擦力、库仑摩擦力、粘性摩擦力和拖动摩擦力。其中静摩擦力是在物体运动速度为零时所受的摩擦力，此时，只要物体所受的作用力小于最大静摩擦力，则静摩擦力始终与施加于物体的作用力相平衡。静摩擦力通常只能通过实验来描述。库仑摩擦力是一种机械阻尼力，其中的能量是通过滑动摩擦而消耗的，由彼此挤压的2个表面的相对运动所产生，库仑摩擦总是抵抗相对运动并且与法向接触力成比例。粘性摩擦力是物体运动时的阻力，粘性摩擦力抵抗任何物体通过接触与另一物体产生相对运动。对应于系统具有良好润滑的情况，粘性摩擦力与速度成比例。拖动摩擦力是固体物体与液体或气体之间的摩擦力，与速度的平方成比例。

各种复杂摩擦力模型主要都采用静摩擦力、库仑摩擦力、粘性摩擦力和拖动摩擦力的不同组合形式作为系统所受摩擦力模型的基本构成[19]。

1.3 系统建模

为了确定摩擦传动的压电定位台控制系统所受各种摩擦力的情况，首先设计了三角函数波(周期为6 s，正向幅值为1.5 V，负向幅值为-2.1 V)作为输入的开环测试信号，此时测得的摩擦传动压电定位台控制系统的响应速度如图3所示。

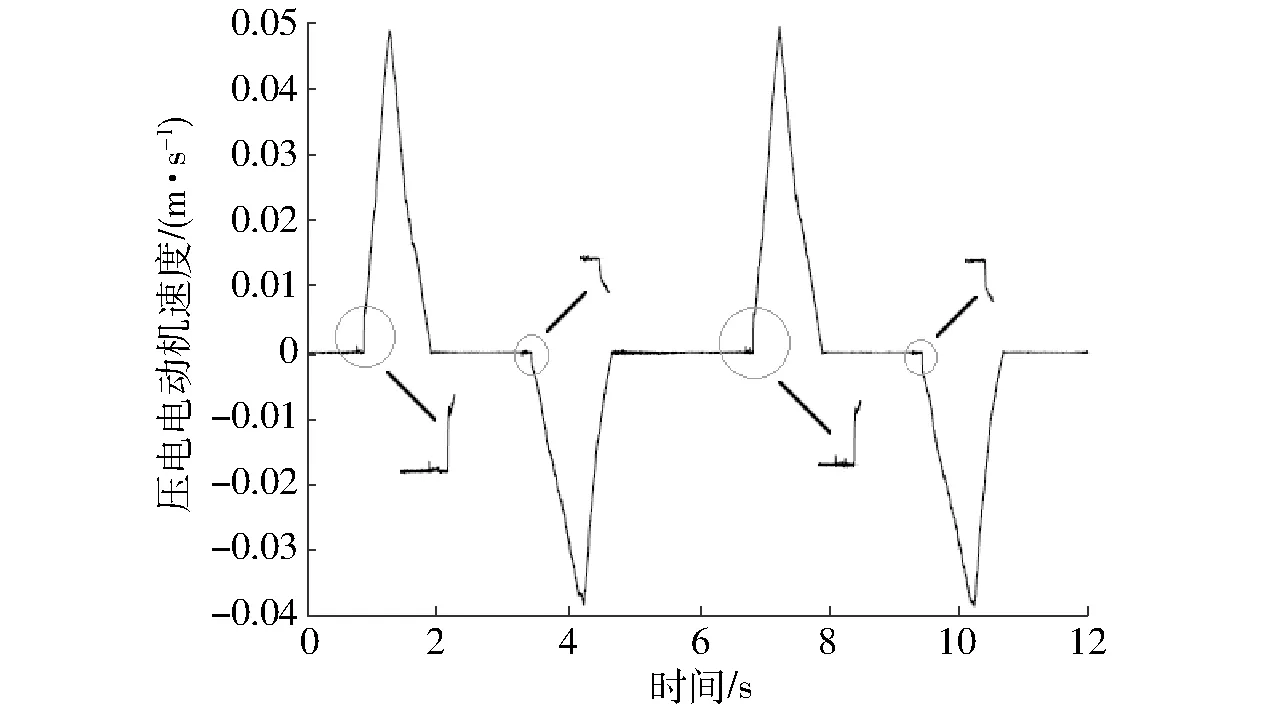
图3 三角波输入时摩擦传动压电定位台的响应速度Fig.3 Response speed of piezoelectric motor positioning stage when a triangular wave input was applied

由图3可以看出，输入作用克服静摩擦力，在速度过零处有明显的跳变。另外，摩擦传动的压电定位台速度很小，固体与空气之间的拖动摩擦因数很小，还有摩擦传动的压电定位台的截面面积也很小，因此拖动摩擦力非常小，可以忽略，建模时可不考虑拖动摩擦力。注意到电动机的正反行程相应的摩擦因数是不同的，根据牛顿第二定律，结合摩擦传动的压电定位台所受的静摩擦力、库仑摩擦力以及粘性摩擦力，摩擦传动的压电定位台系统的模型表示为

(1)

其中

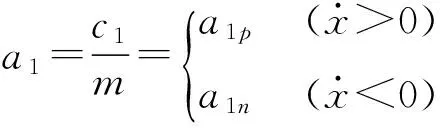
式中m——电动机转子质量Fs——静摩擦力

a1——归一化粘性系数

a2——归一化库仑摩擦系数

a3——摩擦传动的压电定位台系统电压到作用力的转换常数

u——输入电压

图4 摩擦传动压电定位台的脉宽输入响应速度Fig.4 Pulse-width input response speed of piezoelectric motor positioning stage

根据PBA Systems公司PLS8-115型摩擦传动压电定位台系统说明[20]，可确定a3=6 N/(V·kg)。

为了确定模型中的其余常数，可以先设计脉宽冲击响应来确定，并且脉宽幅值大于最大静摩擦力，采用这样的测试，可以使系统的响应受静摩擦力的影响最小。为此，首先输入脉冲宽度是0.4 s，幅值为-2.3 V和1.6 V的脉宽冲击信号，可以得到系统响应如图4所示。

由图4可以得到方程

(2)

选用完全相同的方法，选择的脉宽仍为0.4 s，脉宽信号的幅值分别为-1.8 V和1.3 V，-2 V和1.5 V，-2.1 V和1.7 V，-2.5 V和2 V，这样可以得到参数辨识的方程为

XA=Y

(3)

其中

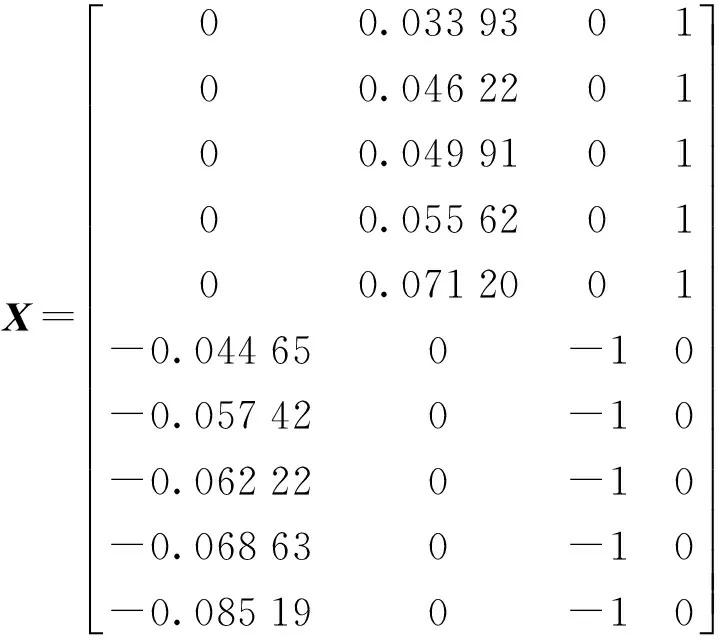
记

es=Y-XA

(4)

(5)

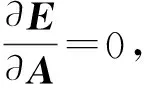
(6)

由此可解得

A=(XTX)-1XTY

(7)

可以得到a1p=104.015 4，a1n=117.144 1，a2p=3.102 3，a2n=6.821 6。

将所得参数代入模型，此时不考虑静摩擦力，可得模型仿真输出与实验测试结果对比如图5所示。

从图5中可以看出，粘性摩擦力有一定的滞后，通过对粘性摩擦力的作用加入延时，反复测试，在粘性摩擦力滞后0.003 5 s时，可以得到此时模型的仿真输入与实验测试结果的比如图6所示。

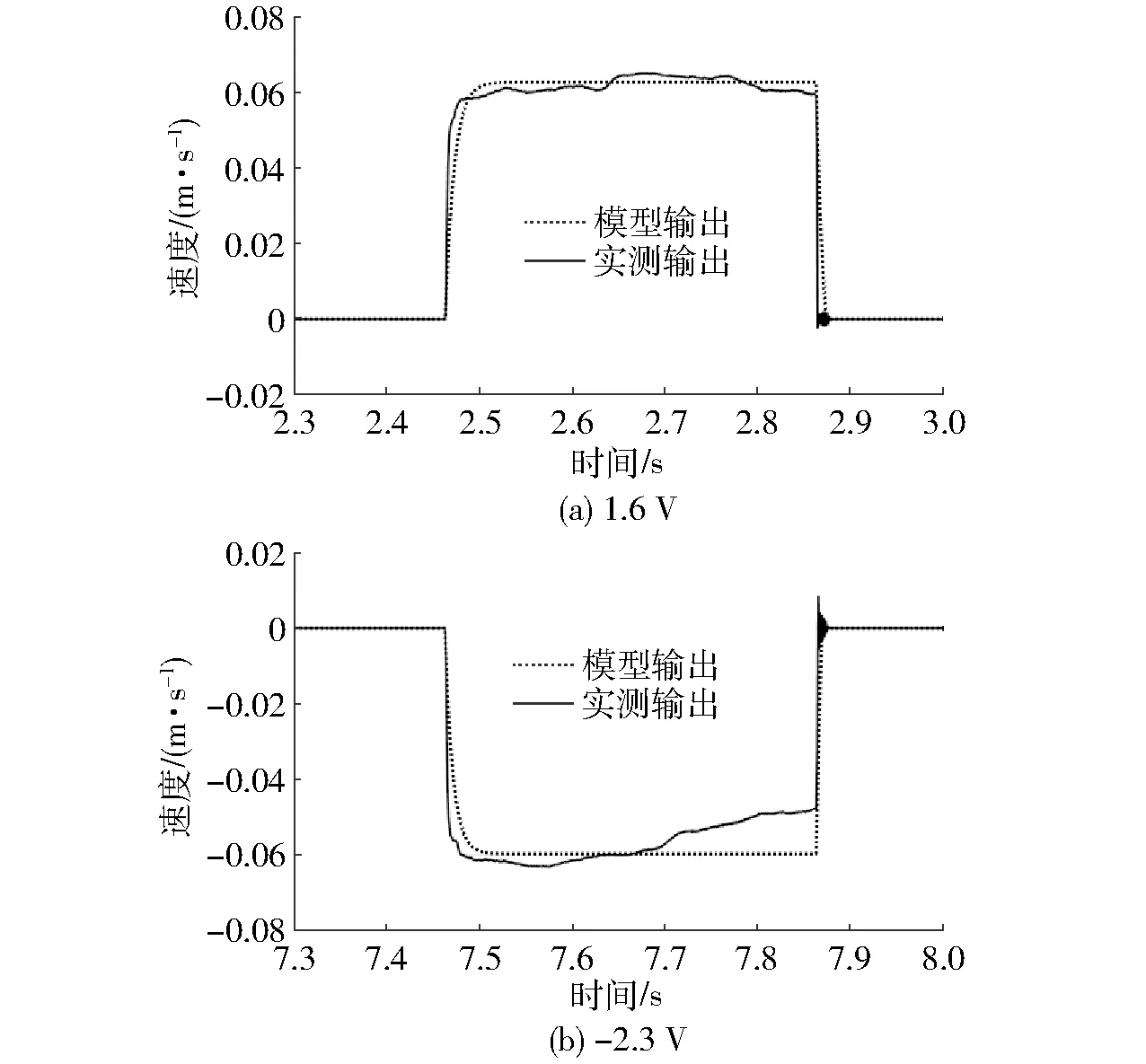
图5 0.4 s脉冲宽度脉冲振幅作用下的速度对比曲线Fig.5 Contrast curves of velocity under acting of 0.4 s pulse width with of pulse amplitude

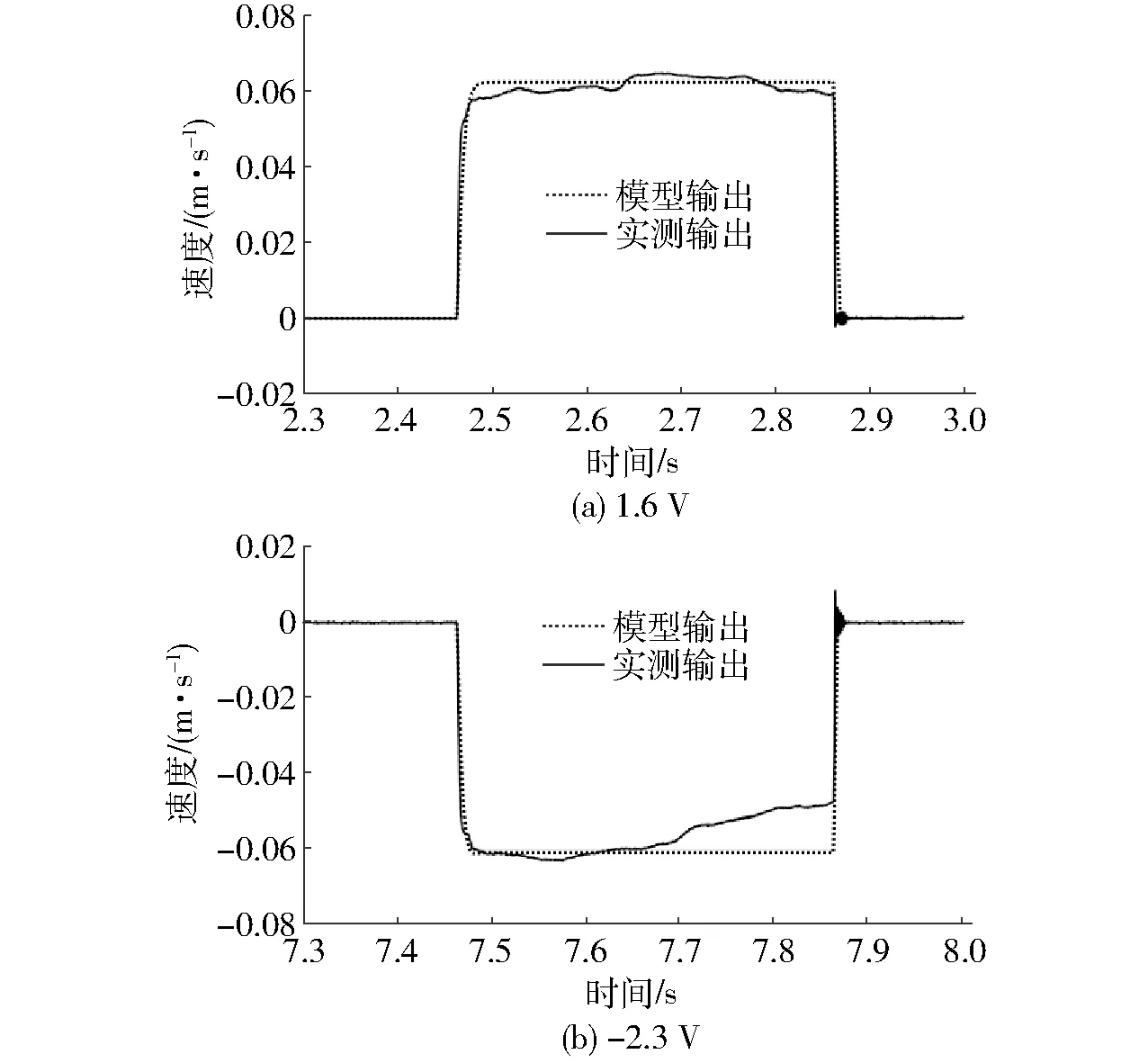
图6 0.4 s脉冲宽度、脉冲振幅作用下的速度对比曲线(粘性摩擦力滞后)Fig.6 Contrast curves of velocity under acting of 0.4 s pulse width of pulse amplitude (viscous friction hysteresis)

静摩擦力的准确仿真是很难实现的，此时系统速度为零，用于摩擦传动的压电定位台控制系统设计的模型为

(8)

其中

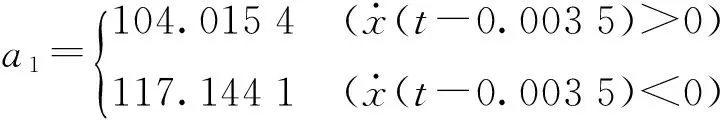
运用该模型，输入选用三角函数波(周期为6 s，正向幅值为1.5 V，负向幅值为-2.1 V)信号，可得模型输出与摩擦传动的压电定位台系统的实测输出如图7所示。由图7可以看出，尽管存在一定误差，但用于控制方法设计，还是可以比较准确地反映摩擦传动的压电定位台系统的输出。

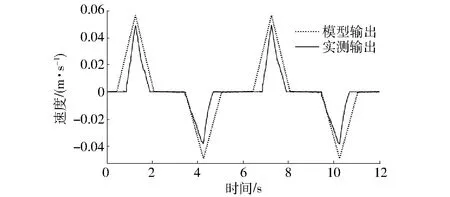
图7 三角函数(振幅为1.5 V，-2.1 V，周期为6 s)输入作用下的速度对比曲线Fig.7 Contrast curves of velocity under triangle wave input signal acting of 0.4 s period with -2.1 V and 1.5 V of amplitude

2 控制方法设计与测试

跟踪的位置信号如图8所示。

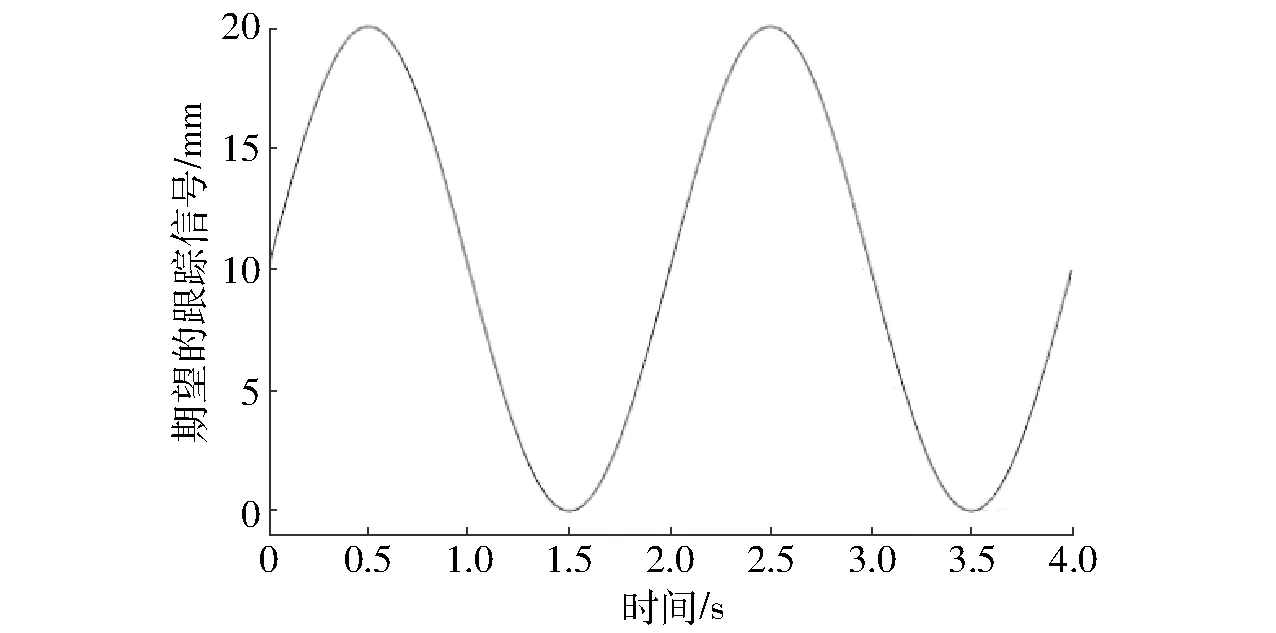
图8 期望的跟踪信号Fig.8 Desired tracking signal

根据系统建模结果，选择模型补偿加滑模控制作为系统的控制方案，控制系统结构如图9所示。

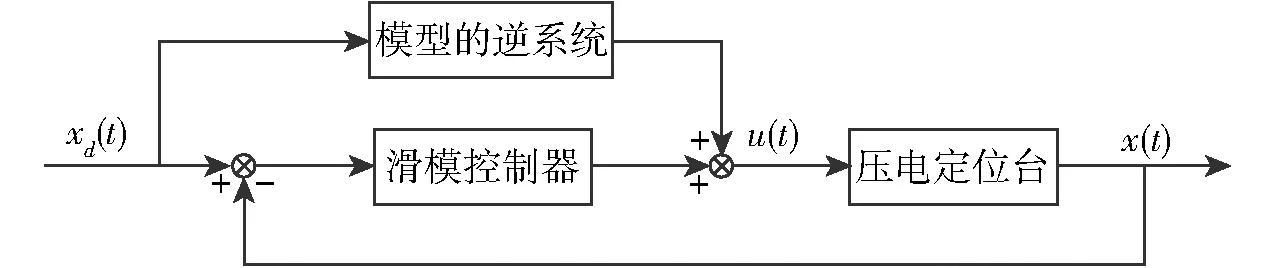
图9 压电定位台控制系统结构图Fig.9 Structure of piezoelectric motor positioning stage control system

先将滑模面定义为

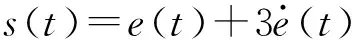
(9)

其中

e(t)=xd(t)-x(t)

式中e(t)——跟踪误差

xd(t)——期望的跟踪信号

x(t)——实际的位置信号

将控制器设计为

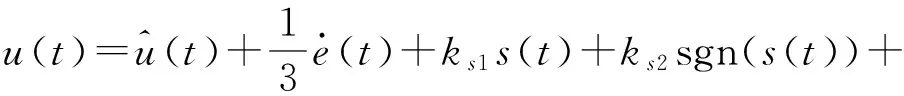
(10)

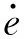
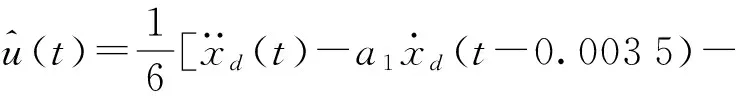
(11)

设实际系统可以描述为

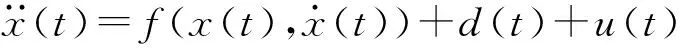
(12)

其中d(t)为系统干扰，该值非常小，设实际系统与建模结果存在如下关系

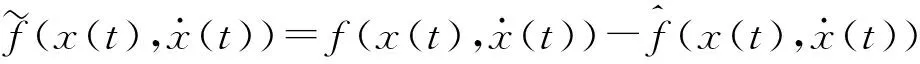
(13)

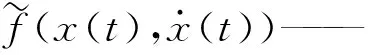
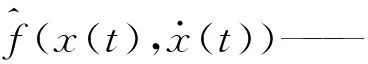
对于系统(12)选用控制器(10)，合理设计控制器中的参数，系统(12)是稳定的，选择如下正定的Lyapunov函数，为了书写简便，下面的论证省去时间变量t。

(14)

则

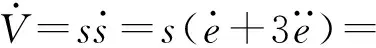
(15)

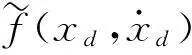
(16)

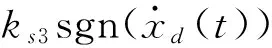
作为对比，首先选用传统的PI控制器作为系统的控制信号，通过调整比例系数KP和积分系数KI，通过实验可得，在系统不产生振荡时，以误差最小作为PI控制器参数的选取依据，由此，可得KP=26 000，KI=2 400，此时系统的误差如图10所示。

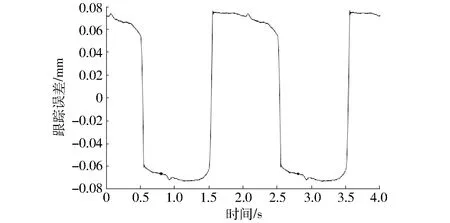
图10 PI控制时系统的跟踪误差Fig.10 Tracking error of PI control

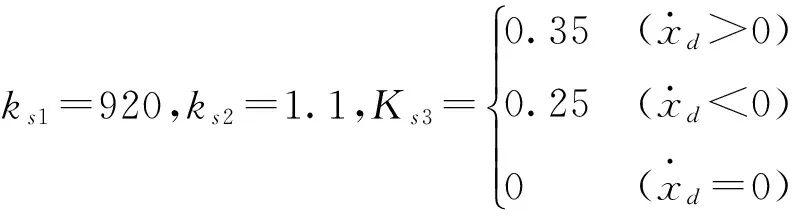
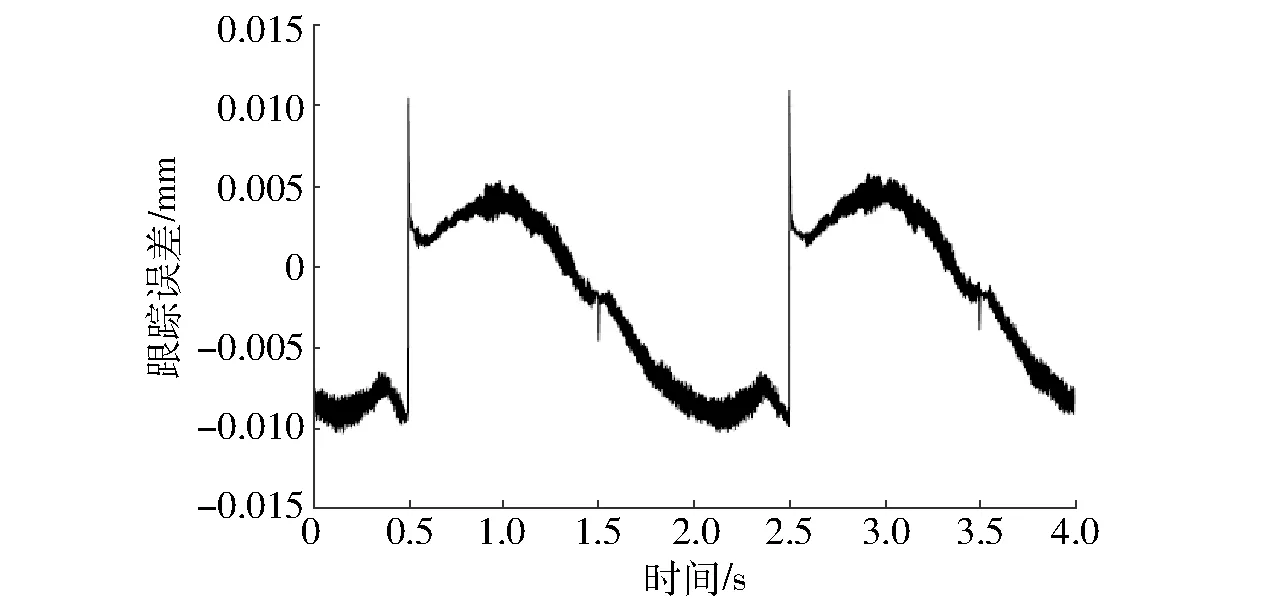
图11 模型补偿加滑模控制时系统的跟踪误差Fig.11 Tracking error of inverse system compensation plus sliding mode control

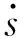
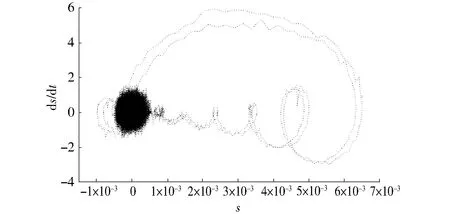
图12 s与的关系Fig.12 Relationship between s and

3 结论

(1)通过采用逆系统模型补偿结合滑模控制，可以达到很高的控制精度，对于本文采用的摩擦传动的压电定位台，所得到的最大跟踪误差为0.010 95 mm，相对误差达到0.054%。

(2)对于采用摩擦传动的系统，由于静摩擦力的影响，速度在过零时会产生较大误差，但此时速度为零，难以建模，如能及时有效补偿传动时系统所受的静摩擦力，控制精度可以进一步提高。

(3)逆系统的输出作为前馈控制对提高控制精度起主要作用，因此系统建模的精度越高，则逆系统补偿后，误差越小，此时需要的滑模控制补偿作用就越小，系统的性能就会越高。

1 邢继春，许立忠，梁永丽. 旋转式惯性压电电机的振子模型研究[J]. 振动与冲击，2010，29(11)：105-109.

XING Jichun，XU Lizhong，LIANG Yongli. A vibrator model for a piezoelectric motor with rotary inertia[J]. Journal of Vibration and Shock，2010，29(11)：105-109.(in Chinese)

2 王亮,舒承有,金家楣. 用于驱动履带的夹心式压电作动器的动力学特性[J]. 机械工程学报, 2017, 53(5): 128-135.

WANG Liang, SHU Chengyou, JIN Jiamei. Dynamical characteristics of sandwich-type piezoelectric actuator for driving track[J]. Journal of Mechanical Engineering, 2017, 53(5): 128-135.(in Chinese)

3 梁克平，邵培革，杨敬涵. 串联臂压电微电机及驱动电源的研究[J]. 仪器仪表学报，2001，22(5)：510-511.

LIANG Keping，SHAO Peige，YANG Jinghan. Driving mechanism and the driving circuit of a micromotor driven by series bending vibrating piezoelectric arms[J]. Chinese Journal of Scientific Instrument，2001，22(5)：510-511.(in Chinese)

4 张明辉，李满天，孙立宁. 基于压电陶瓷平面内应变的多自由度超声波电机驱动电路研究[J]. 中国电机工程学报，2007，27(33)：30-35.

ZHANG Minghui，LI Mantian，SUN Lining. Driving circuit for multi-degree of freedom ultrasonic motor using in-plane deformation of PZT elements[J]. Proceedings of the Chinese Society for Electrical Engineering，2007，27(33):30-35.(in Chinese)

5 孙合明，赵淳生，朱晓东. 纵扭型压电超声电机的摩擦特性仿真研究[J]. 东南大学学报:自然科学版，2002，32(4)：624-626.

SUN Heming，ZHAO Chunsheng，ZHU Xiaodong. Simulation on friction characteristic of ultrasonic motor using longitudinal and torsional mode[J]. Journal of Southeast University: Natural Science Edition ，2002，32(4)：624-626.(in Chinese)

6 SALAPAKA S M, SALAPAKA M V. Scanning probe microscopy[J]. IEEE Control Systems, 2008, 28(2): 65-83.

7 CLAYTON G M, TIEN S, LEANG K K, et al. A review of feedforward control approaches in nanopositioning for high-speed SPM[J]. Journal of Dynamic Systems, Measurement, and Control, 2009, 131(6): 61-101.

8 CHOI G S, LIM Y A, CHOI G H. Tracking position control of piezoelectric actuators for periodic reference inputs[J]. Mechatronics, 2002, 12(5): 669-684.

9 SHAN Y, LEANG K K. Accounting for hysteresis in repetitive control design: nanopositioning example[J]. Automatica, 2012, 48(8): 1751-1758.

10 KWON K, CHO N, JANG W. The design and characterization of a piezo-driven inchworm linear motor with a reduction-lever mechanism[J]. JSME International Journal, 2005, 47(3):803-811.

11 PAN Q, HUANG F, CHEN J. High-speed low-friction piezoelectric motors based on centrifugal force[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 2158-2167.

12 RAKOTONDRABE M, HADDAB Y, LUTZ P. Quadrilateral modelling and robust control of a nonlinear piezoelectric cantilever[J]. IEEE Transactions on Control Systems Technology, 2009, 17(3): 528-539.

13 GU G Y, ZHU L M. An experimental comparison of proportional-integral, sliding mode, and robust adaptive control for piezo-actuated nanopositioning stages[J]. Review of Scientific Instruments, 2014, 85(5): 106-112.

14 CHEN X, HISAYAMA T. Adaptive sliding-mode position control for piezo-actuated stage[J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 3927-3934.

15 郭亚子,朱玉川. 压电叠堆执行器迟滞非线性建模与分析[J]. 压电与声光, 2017, 39(4):520-524.

GUO Yazi, ZHU Yuchuan. Modeling and analysis on hysteresis nonlinear characteristics of the piezoelectric stack actuators[J]. Piezoelectrics & Acoustooptics, 2017, 39(4):520-524.(in Chinese)

16 王硕,滕兆春. 加热压电纤维复合材料圆板的横向自由振动[J]. 计算力学学报,2017, 34(3):286-291.

WANG Shuo, TENG Zhaochun. Transverse free vibration of heated piezoelectric fibre composite materials circular plates[J]. Chinese Journal of Computational Mechanics, 2017, 34(3):286-291.(in Chinese)

17 黄健萌,黄靖.压电驱动微悬臂梁与基底粗糙面间多次接触分析[J/OL].农业机械学报,2015,46(9):368-372.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150954&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.09.054.

HUANG Jianmeng, HUANG Jing. Multiple-contact analysis between microcantilever and substrate rough surface driven by piezoelectric[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9):368-372.(in Chinese)

18 陈希,王海,陶伟. 基于压电陶瓷的柔性机械臂主动振动控制实验研究[J]. 传感技术学报, 2017, 30(5):777-781.

CHEN Xi, WANG Hai, TAO Wei. Experimental study of active vibration control of flexible manipulator based on piezoelectric ceramic elements[J]. Chinese Journal of Sensors and Actuators, 2017, 30(5):777-781.(in Chinese)

19 BASHA W, GHALY W S. Drag prediction in transitional flow over airfoils[J]. Journal of Aircraft, 2007, 44(3): 824-832.

20 Piezo linear stage-PLS8 reference[Z].PBA Systems Pte Ltd.，2009.