基于Rayleigh-Plesset方程的空化模型改进与应用

洪 锋 高振军 袁建平

(1.三峡大学机械与动力学院， 宜昌 443002； 2.三峡大学水电机械设备设计与维护湖北省重点实验室， 宜昌 443002；3.江苏大学国家水泵工程技术研究中心， 镇江 212013)

0 引言

空化是一种包含相变、介质压缩性、粘性及湍动效应的复杂多相流。在水力机械领域，空化的发生总会造成不同程度的负面作用。迄今为止，空化和空泡动力学特性一直是国际水动力学界的热点和前沿科学问题[1]。

当前，应用于工程问题中的空化数值模型大部分是由只考虑空泡半径一阶导数项及压力驱动项的Rayleigh-Plesset(R-P)方程推导而来[2-8]，该类模型没有考虑二阶导数项、粘性项及表面张力项对空泡半径增长的影响。文献[9]指出，完整R-P方程中的二阶导数项对超声诱导空泡半径的增长有着重要的影响，且不可被忽略；基于简化R-P方程的空化模型在模拟绕水翼及螺旋桨空化流场时均存在不足之处[10-11]。上述3种空化模型在推导过程中只考虑了两种组分(空泡相和液相)，而实际流体中还包含了不可凝结的气体(NCG)，一个标准大气压下纯水所能溶解NCG的饱和质量浓度为1.5×10-5mg/L。该部分气体在空化发生过程中充当空化核，空化核对空化初生有着重要的作用[12]。

为了改善这种基于简化R-P方程的空化模型模拟空化流动的能力，本文基于一种改进的R-P球形空泡动力学模型、液相-空泡相-不可凝结气体相3种组分的连续性方程和均相流假设推导一种修正的R-P模型；然后运用UDF(User-define function)技术，把该模型嵌入到ANSYS FLUENT 14.5平台，并联立一种改进的滤波器湍流模型(MFBM)对绕二维Clark-Y水翼的非定常空化流场进行数值计算。通过与Schnerr-Sauer(S-S)空化模型的数值计算结果及文献中公开的实验结果作对比，以验证修正的R-P模型在预测非定常空化流动特征的可行性及准确性。

1 基于R-P方程的改进空化模型

广义的空泡动力学方程为[12]

(1)

式中R——空泡半径νl——液相运动粘度

S——表面张力系数

pB(t) ——空泡内压力

p∞(t)——无穷远处压力

ρl——液相密度t——时间

等号左边依次为二阶导数项、一阶导数项、粘性项和表面张力项，等号右边为压力驱动项。式(1)中二阶导数项在空泡体积急剧变化时发挥重要作用，而粘性项与表面张力项对空泡半径变化的影响尚不明确，因此研究两种简化形式的空泡动力学模型

(2)

(3)

利用Matlab软件，采用4～5阶RUNGE-KUTTA算法分别对式(2)和式(3)进行求解。假定初始半径为R0的空化核在时间为0时进入低压区，可以得到该空化核流过低压区时R(t)的一个典型解，如图1(图中T表示球形空泡生长周期)所示。从图中可以看到，在t=10T之后，粘性项对空泡半径变化的影响较小，且相比于表面张力项，粘性的影响是可以忽略不计的，这主要是因为液态水及因空化形成的空泡均属于低粘度工质，其运动粘度系数为10-6数量级。

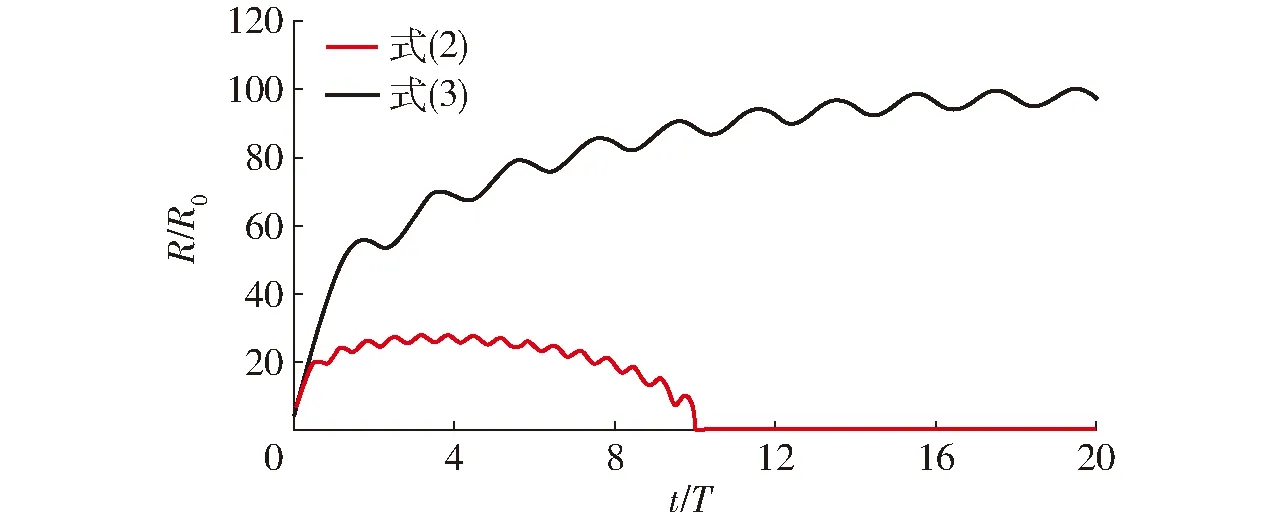
图1 不同空泡动力学模型计算得到的空泡增长过程Fig.1 Variation of bubble radium based on different bubble dynamic models

因此，考虑由压力驱动项、空泡一阶导数项、二阶导数项及表面张力项所组成的动力学模型，如式(3)所示。将式(3)左右两边同时乘以2R2dR/dt，应用初始条件DR/Dt(0)=0[12]积分可以得到

(4)

因此，改进后的球形空泡动力学方程为

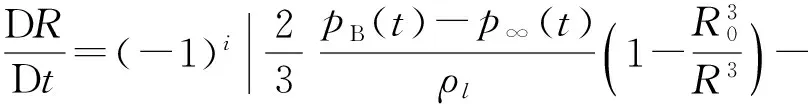
(5)

当i=1时表示凝结过程；当i=2时表示蒸发过程。

为了真实反映空化流动的本质，将介质处理成空泡相、液相及不可凝结气体的混合物，但是空化引起的质量传输过程只在液相和空泡相之间产生，且液相、空泡相及不可凝结气体相3种组分的连续性方程分别为

(6)

(7)

(8)

其中

αl+αv+αg=1

(9)

式中ρ——混合密度V——速度

Se——蒸发率Sc——凝结率

α——体积分数

下标l、v和g分别代表液相、空泡相和不可凝结气体相。

均相流思想是把介质假想成一种均匀的液相-空泡相-不可凝结气体的混合物，这种处理方式可以避免因求解每一组分独立的连续性方程及其动量方程所需要的巨大数值耗散时间。同时，假定各组分之间无相对滑移速度，即

Vl=Vv=Vg=V

(10)

式(6)～(8)相加，可以得到混合相的连续性方程，即

(11)

混合密度ρ及混合动力粘度系数μ分别表示为

ρ=αlρl+αvρv+αgρg

(12)

μ=αlμl+αvμv+αgμg

(13)

在单元控制体内，为了解决液相与空泡相之间由于发生相变而产生剧烈的相对密度变化引起的数值计算困难，故使用一种非守恒型连续性方程来描述混合流体的运动。该方程为[13]

(14)

因为

(15)

由式(10)及式(15)可得

(16)

由式(9)可得

(17)

把式(16)代入到式(17)可得

(18)

联立式(12)、(14)及(18)可得

(19)

把式(19)代入到式(7)中可得

(20)

空泡体积分数αv由空泡半径R及单位体积内空泡数量N0表示[7]，即

(21)

由式(21)可推导出

(22)

将式(22)代入到式(20)可得

(23)

把式(5)代入到式(23)中可得最终形式的蒸发率表达式为

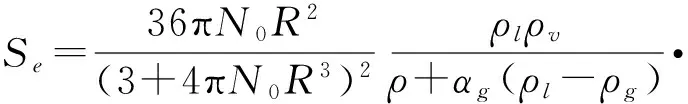
(24)

同理，最终形式的凝结率表达式为

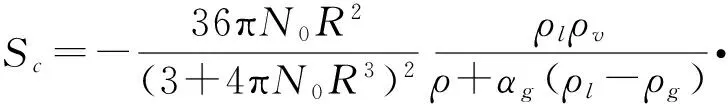
(25)

N0=1×1013m-3、R0=1 μm，NCG的体积分数计算公式为

αg=fgρ/ρg

(26)

ρg按照密度形式理想气体状态方程计算，质量分数fg=1.5×10-6。

计算时为了考虑湍流脉动对空化初生的影响，将空化压力pv修正为

pv=psat+0.195ρk

(27)

式中psat——饱和蒸汽压，取3 169 Pa

k——湍动能

式(24)～(27)所组成的数学模型即为修正的R-P模型。该模型与Schnerr-Sauer(S-S)模型均是基于均相流理论建立，也都采用式(20)来描述空泡体积分数与空泡半径及单位体积内空化核数量之间的关系，但是修正的R-P模型具有以下优点：①修正的R-P模型把空泡流真实地还原成液相、空泡相及不可凝结气体的混合物，而S-S模型则把介质处理成由液相和空泡相组成的混合物。②修正的R-P模型推导是基于改进后的Rayleigh-Plesset空泡动力学方程，该方程考虑了空泡半径的二阶变化及表面张力的影响。③修正的R-P模型考虑了湍流脉动对空化初生的影响。

2 修正的滤波器湍流模型(MFBM)

湍流模型的合理选取对空化流动数值计算尤其重要，传统的双方程湍流模型会过度预测闭合空穴尾部的湍流粘度，从而会阻止回射流向水翼前缘运动，使得空穴脱落不会被预测到，而直接模拟或者大涡模拟会消耗大量的计算机资源，尤其在实际的水力机械计算中这一问题会显得更加突出[14]。因此，本文采用文献[15]中提出的一种修正的滤波器湍流模型(MFBM)。MFBM实际上是一种修正的RNGk-ε的混合模型，模型的思想是通过一个函数fMFBM联立滤波器模型(FBM)和密度修正模型(DCM)来共同修正传统RANS模型的湍流粘度，从而使得修正后的模型兼备FBM和DCM的优点。基于RNGk-ε模型修正后的湍流粘度系数为

(28)

其中

fMFBM=min(fDCM,fFBM)

(29)

(30)

(31)

式中λ——滤波尺寸

n=10，Cμ=0.09，C3=1.0。

3 计算网格及边界条件

以二维Clark-Y型水翼作为研究对象，翼型弦长c=70 mm，攻角A=8°。计算域为矩形，其宽度和长度分别为2.7c和10c，水翼前缘到计算域进口距离为3c，水翼尾缘到计算域出口距离为6c，该水翼的空化水洞实验由王国玉等[16-19]完成。边界条件设定均与文献[16]保持一致，即入口采用速度入口，计算域进口速度Uin=10 m/s，出口采用压力出口，通过调整出口压力，从而获取相应的空化数条件。计算域上下边界均为自由无滑移壁面条件，为获得更精确的计算结果，翼型壁面函数选择增强型壁面条件。

对计算域划分了4种不同尺寸的网格，并作网格无关性分析来消除网格数量造成的计算误差。不同网格方案对应的网格节点数分别为N1=59 576，N2=106 523，N3=157 296及N4=198 776。通过计算空化数σ=0.8条件下水翼上下表面压力系数Cp随网格节点数的变化规律来确定最终的计算网格。计算结果如图2所示，从图中可以看出，不同网格方案计算得到的翼型上表面压力分布随着网格节点数的增加逐渐趋于一致。细网格与极细网格之间的压力分布几乎相等，表明继续增大网格数量对计算结果影响可以忽略不计，因此最终选择细网格作为本文的计算网格。

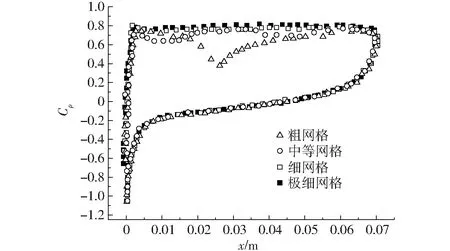
图2 网格无关性分析Fig.2 Mesh independence analysis

4 计算结果分析

为了研究修正的R-P模型对水翼空化流场的模拟效果，采用数值计算的方法得到了Schnerr-Sauer模型及修正的R-P模型对片状空化(σ=1.4)及云状空化(σ=0.8)两种典型空化条件下翼型所受的水动力系数及其吸力面上的空穴形态分布规律，并与文献中的实验结果作对比。数值计算均采用非定常求解器，时间步长Δt依据CFL条件(Courant-Friedrichs-Lewy condition)确定[1]，结合计算成本，最终取Δt=1.0×10-6s。定义空化数、升力系数、阻力系数及空泡总体积分别为

(32)

(33)

(34)

(35)

式中pout——出口压力N——网格单元总数

Fl——升力Fd——阻力

L——翼型展向长度

αi——网格单元内的空泡体积分数

Vi——网格单元的体积

4.1 准静态片状空化

张博等[20]对Clark-Y型水翼片状空化进行了大量实验研究。根据实验结果，当空化数降低至σ=1.4时，片状空化逐渐形成，此时翼型前缘附着透明的空泡，而翼型尾缘处存在波动，且有较小的空泡团脱落。

图3为两种模型模拟得到的4个不同时刻空泡体积分数分布图，从图中可以看到，在翼型前缘处，S-S模型得到的高质量分数的空化区逐渐减小，表明该处结构稳定的片状空穴长度发生了波动，这与实验结果不符。相比较而言，采用修正的R-P模型计算得到的片状空穴长度基本上维持不变，而且在空穴尾部出现了明显的相间破碎界面并伴有体积分数较低的空泡团脱落现象，而这与实验结果的吻合度较好。同时，不同空化模型计算得到的平均升力、阻力系数对比如表1所示，从表中可以看到，相比于S-S模型，修正的R-P模型模拟得到的平均升阻力系数与实验值吻合度更好。综上分析，修正的R-P模型对片状空穴长度、空穴闭合末端流动细节的捕捉能力以及对水动力系数预测的能力均优于S-S模型。

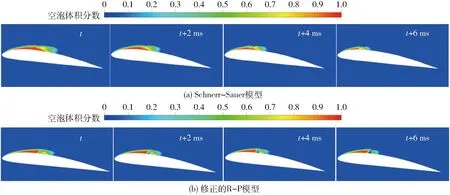
图3 两种不同空化模型计算得到的片状空穴形态对比Fig.3 Comparisons of evolution of sheet cavitation predicted by Schnerr-Sauer and proposed models

模型类型 Cl Cd计算值实验值[18]相对误差/%计算值实验值[18]相对误差/%修正的R-P模型1.0511.169.390.0390.0414.88Schnerr-Sauer模型1.0341.1610.860.0370.0419.76

4.2 周期性云状空化

依据文献[21]，当空化数降低至σ=0.8时，翼型前缘处附着的片状空穴所表现出的不稳定性加剧，其长度和厚度都明显增加，且尾缘处大体积空泡团脱落现象也更加显著。

图4为两种模型计算得到的瞬时升力系数与实验值[21]的对比。从图中可以看到，修正的R-P模型模拟得到的瞬时升力系数与实验值的变化趋势吻合程度更好，而S-S模型模拟得到的升力系数出现了较多的波动。表2所示为不同空化模型模拟得到的平均升力、阻力系数与实验值对比，从表中可以看到，修正的R-P模型模拟得到的平均升力系数与实验值吻合度更好，其相对误差仅为6.93%，且修正的R-P模型预测到的平均阻力系数相比于Schnerr-Sauer模型预测结果也与实验值更接近。Schnerr-Sauer模型模拟得到的平均升、阻力系数与实验值的相对误差均超过10%。

图5所示为两种空化模型计算得到的空泡总体积随时间变化图，从图中可以看到，二者计算得到的空泡体积随时间呈较为明显的周期性变化，且修正的R-P模型和S-S模型计算得到的云状空化平均演变周期分别为T1=45.5 ms和T2=38.4 ms，实验观测到的云状空化演变周期为T3=50 ms[18]。由此可见，修正的R-P模型在模拟云状空化周期性变化过程时相比于S-S模型更具有优越性；另一方面，修正的R-P模型模拟得到的空泡体积明显大于S-S模型，表明非线性模型可以计算得到面积更大的空化区域，这主要是由于修正的R-P模型考虑了NCG、湍流脉动对空化初生的影响。

图6(图中t0表示翼型尾缘处空泡团体积增长至最大的时刻)所示为模拟得到的一个周期内云状空化演变与实验结果[21]的对比，图6a～6e为实验结果，图6f～6j为修正R-P模型的预测结果，图6k～6o为S-S模型的预测结果。对比可以发现，不同空化模型模拟得到的空泡演变过程都基本上反映出了云状空化中位于翼型前缘处片状空穴长度和厚度的增长，以及随后云状空化脱落和向下游溃灭的周期性变化过程。但是，二者的不同之处主要有以下4点：总体上来看，不同时刻修正的R-P模型模拟得到的空化区域均大于S-S模型的模拟结果；在t=t0时刻，片状空穴回缩至翼型前缘几乎消失，尾缘处空泡形成团状结构并开始逐渐脱离壁面，对比发现，修正的R-P模型预测到的空泡团尺寸与实验拍摄到的结果更加吻合，且空泡团位置仍靠近翼型尾缘，而S-S模型预测到的空泡团已经离开翼型吸力面；在t=t0+58%Ti(i=1、2、3)时刻，空穴内部表现出强烈的不稳定性且两相界面出现明显的破碎，对比可以发现S-S模型预测的界面破碎程度要高于修正的R-P模型的模拟结果，而空穴内强烈的不稳定性与回射流结构有着紧密联系[1]，表明S-S模型预测到的回射流强度大于修正的R-P模型的预测结果；在t=t0+84%Ti(i=1、2、3)时刻，实验结果中的空穴长度近似为0.5倍弦长，S-S模型模拟的空穴长度明显偏小。综上分析，尽管两个空化模型均可以模拟出云状空化周期性演变过程，但在一些空化流动细节的捕捉上，修正的R-P模型更具有优越性。

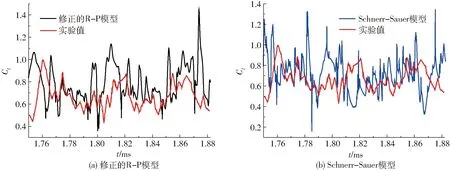
图4 两种模型模拟得到的升力系数与实验值对比Fig.4 Comparisons of transient lift coefficients of simulation and experiment

模型类型ClCd计算值实验值[18]相对误差/%计算值实验值[18]相对误差/%修正的R-P模型0.7520.8086.930.1280.11511.30Schnerr-Sauer模型0.7230.80810.520.1310.11513.91

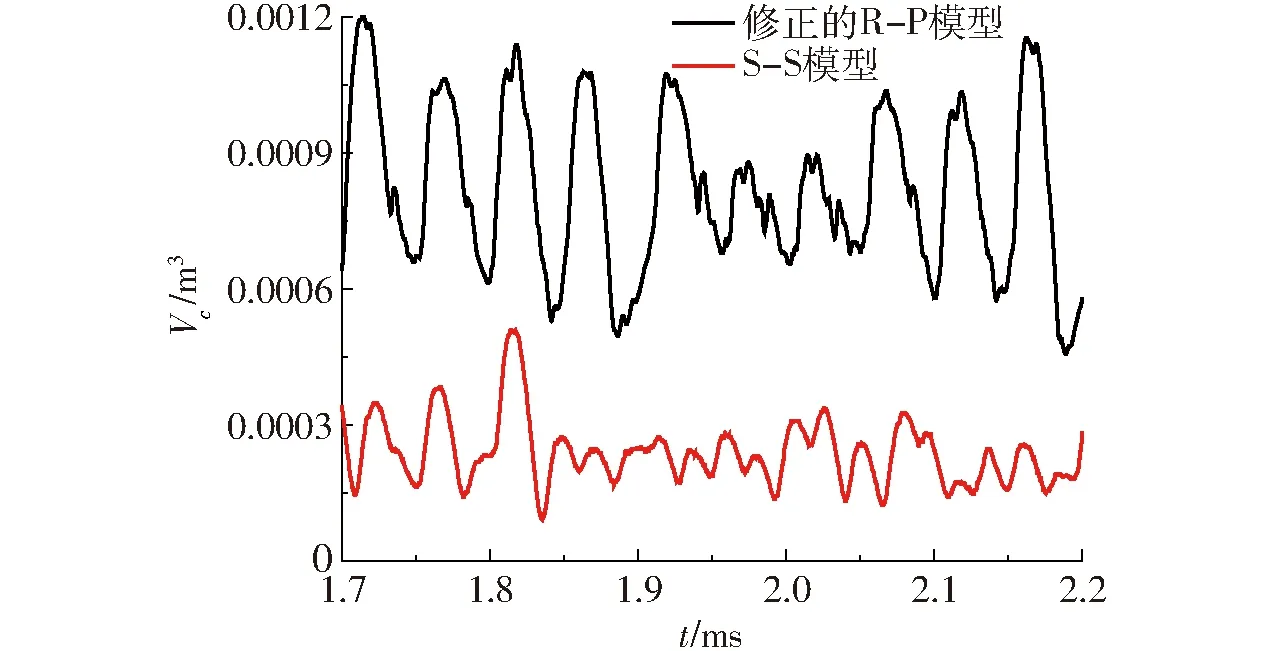
图5 两种模型模拟得到的空泡总体积对比Fig.5 Comparisons of total vapor volume of simulations by using two models

图6 两种模型模拟得到的云空化演变与实验值对比Fig.6 Comparisons of predicted evolution of cloud cavitation of simulations and experiment by two models

5 结论

(1)在准静态片状空化阶段，修正的R-P模型计算得到的片状空穴长度基本上维持不变，而且在空穴尾部出现了明显的相间破碎界面并伴有体积分数较低的空泡团脱落现象，与实验描述较为一致。

(2)修正的R-P模型与Schnerr-Sauer模型预测云空穴演变平均周期分别为45.5 ms和38.4 ms，且修正的R-P模型能较清晰地预测云状空泡的初生、发展、溃灭和脱落的全过程。

(3)云空化阶段，修正的R-P模型模拟得到的瞬时升力系数与实验值的变化趋势吻合程度更高，尽管两个空化模型均可以模拟出云状空化周期性演变过程，但在一些流动细节的捕捉上，修正的R-P模型对云空化周期性演变的预测能力更好。

(4)修正的R-P模型联立改进的滤波器湍流模型，联合求解绕水翼非定常空化流动具有较高的准确性和可行性。

1 洪锋，袁建平，周帮伦.空泡半径非线性变化的空化模型及应用[J]．华中科技大学学报，2015，43(10)：15-20.

HONG Feng，YUAN Jianping，ZHOU Banglun. Cavitation model considering non-linear variation of bubble radius and its application [J]. Journal of Huazhong University of Science and Technology，2015，43(10)：15-20. (in Chinese)

2 SINGHAL A K，ATHAVALE M M，LI H，et al．Mathematical basis and validation of the full cavitation model[J]. ASME Journal of Fluids Engineering，2002，124(3)：617-624．

3 RHEE S H, KAWAMURA T, LI H．Propeller cavitation study using an unstructured grid based Navier-Stoker solver[J]．ASME Journal of Fluids Engineering，2005，127(5)：986-994．

4 ATHAVALE M M, LI H Y, JIANG Y U, et al. Application of the full cavitation model to pumps and inducers[J]. International Journal of Rotating Machinery, 2002, 8(1):45-56．

5 ZWART P J，GERBER A G，BELAMRI T．A two-phase flow model for predicting cavitation dynamics[C]∥ICMF Fifth International Conference on Multiphase Flow，2004．

6 LIU H, WANG J, WANG Y, et al．Influence of the empirical coefficients of cavitation model on predicting cavitating flow in the centrifugal pump[J]．International Journal of Naval Architecture and Ocean Engineering, 2014, 6(1): 119-131．

7 SCHNERR G H，SAUER J．Physical and numerical modeling of unsteady cavitation dynamics[C]∥ICMF Fourth International Conference on Multiphase Flow，2001．

8 JI B，LUO X W，ARNDT R E A，et al．Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil[J]．International Journal of Multiphase Flow，2015，68：121-134．

10 MORGUT M，NOBILE E，BILUI．Comparison of mass transfer models for the numerical prediction of sheet cavitation around a hydrofoil[J]．International Journal of Multiphase Flow，2011，37(6)：620-626．

11 杨琼方，王永生，张志宏. 改进空化模型和修正湍流模型在螺旋桨空化模拟中的评估分析[J]. 机械工程学报，2012，48(9)：178-185.

YANG Qiongfang, WANG Yongsheng, ZHANG Zhihong. Assessment of the improved cavitation model and modified turbulence model for ship propeller cavitation simulation[J]. Journal of Mechanical Engineering, 2012, 48(9): 178-185. (in Chinese)

12 BRENNEN C E. Cavitation and bubble dynamics [M]. Cambridge: Cambridge University Press, 2013.

13 YUAN W，SCHNERR G H．Numerical simulation of two-phase flow in injection nozzles： interaction of cavitation and external jet formation[J]．ASME Journal of Fluids Engineering，2003，125(6)：963-969．

14 COUTIER-DELGOSHA O，FORTES-PATELLA R，REBOUD J L，et al．Numerical simulation of cavitating flow in 2D and 3D inducer geometries[J]．International Journal for Numerical Methods in Fluids，2005，48(2)：135-167．

15 LI Z, ZHENG D, HONG F, et al. Numerical simulation of the sheet/cloud cavitation around a two-dimensional hydrofoil using a modified URANS approach [J]. Journal of Mechanical Science & Technology, 2017, 31(1):215-224.

16 HUANG B，YOUNG Y L，WANG G Y，et al．Combined experimental and computational investigation of unsteady structure of sheet/cloud cavitation[J]．ASME Journal of Fluids Engineering，2013，135(7)：071301．

17 黄彪，王国玉，王复峰，等．绕水翼非定常空化流场的实验研究[J]．兵工学报，2012，33(4)：401-407．

HUANG Biao, WANG Guoyu, WANG Fufeng, et al. Experrimental study on unsteady cavitating flow around hydrofoil with particle imaging velocimetry system[J]. Acta Armamentarii, 2012,33(4):401-407. (in Chinese)

18 WANG G Y，SENOCAK I，SHYY W，et al．Dynamics of attached turbulent cavitating flows[J]．Progress in Aerospace Sciences，2001，37(6)：551-581．

19 HUANG B，WANG G Y，YU Z，et al．Detached-eddy simulation for time-dependent turbulent cavitating flows[J]．Chinese Journal of Mechanical Engineering，2012，25(3)：484-490．

20 张博，王国玉，李向宾，等.绕水翼片状空化流动结构的数值与实验研究[J]．工程热物理学报，2008，29(11)：1847-1851．

ZHANG Bo, WANG Guoyu, LI Xiangbin, et al. Analysis of sheet cavitation flow structure by numerical and experimental studies [J]. Journal of Engineering Thermophsics, 2008, 29 (11):1847-1851. (in Chinese)

21 张光建．水翼及轴流泵非定常空化特性数值研究[D]．镇江：江苏大学，2014．

ZHANG Guangjian. Numerical simulation of the unsteady cavitation characteristics in hydrofoil and axial flow pump [D].Zhenjiang: Jiangsu University, 2014. (in Chinese)