足式机器人稳定性判据

张 伏， 郑莉敏， 王 唯， 邱兆美， 王 俊， 毛鹏军， 王甲甲， 马田乐

(河南科技大学农业装备工程学院，河南洛阳 471003)

在自然界中，采用足式步行方式的动物均具有较好的灵活性。随着机器人在社会中的广泛应用，机器人在各种环境下的稳定性判据研究显得尤为重要[1-2]。为使足式机器人能更好地达到自身的运动性能，解决在不平坦地面搜索稳定性最优路径问题[3]，促使其进行稳定作业，更好地服务于社会，本研究主要对足式机器人稳定性的判据进行分析，并对其使用场景进行归纳与总结。

1 机器人稳定性

机器人稳定性是指当机器人处于一个平衡状态时，如果受到外部影响，它会经过一个过渡过程仍然能够回到原来的平衡状态，即运动平稳性。目前足式机器人稳定性的评价指标分为静态稳定性和动态稳定性判别指标。静态稳定性是指在系统发生微小扰动时，运行状态将发生变化，当扰动消失后，系统能恢复到原来的状态下稳定运行的能力。动态稳定性是指系统受到小或大的扰动后，在自动调节和控制装置的作用下，保持较长过程的运行稳定性的能力[4]。

2 机器人稳定性判别依据

2.1 静态稳定性

静态稳定性是在牢固不变的支撑面上保持平稳的一种性能指标。步行机器人在行走时，机体相对地面始终是向前运动的，而重心始终也在移动。机器人的四条腿轮流抬跨，相对机体也是向前运动的，且不断地在改变立足点位置。机器人静态稳定性描述如图1所示。

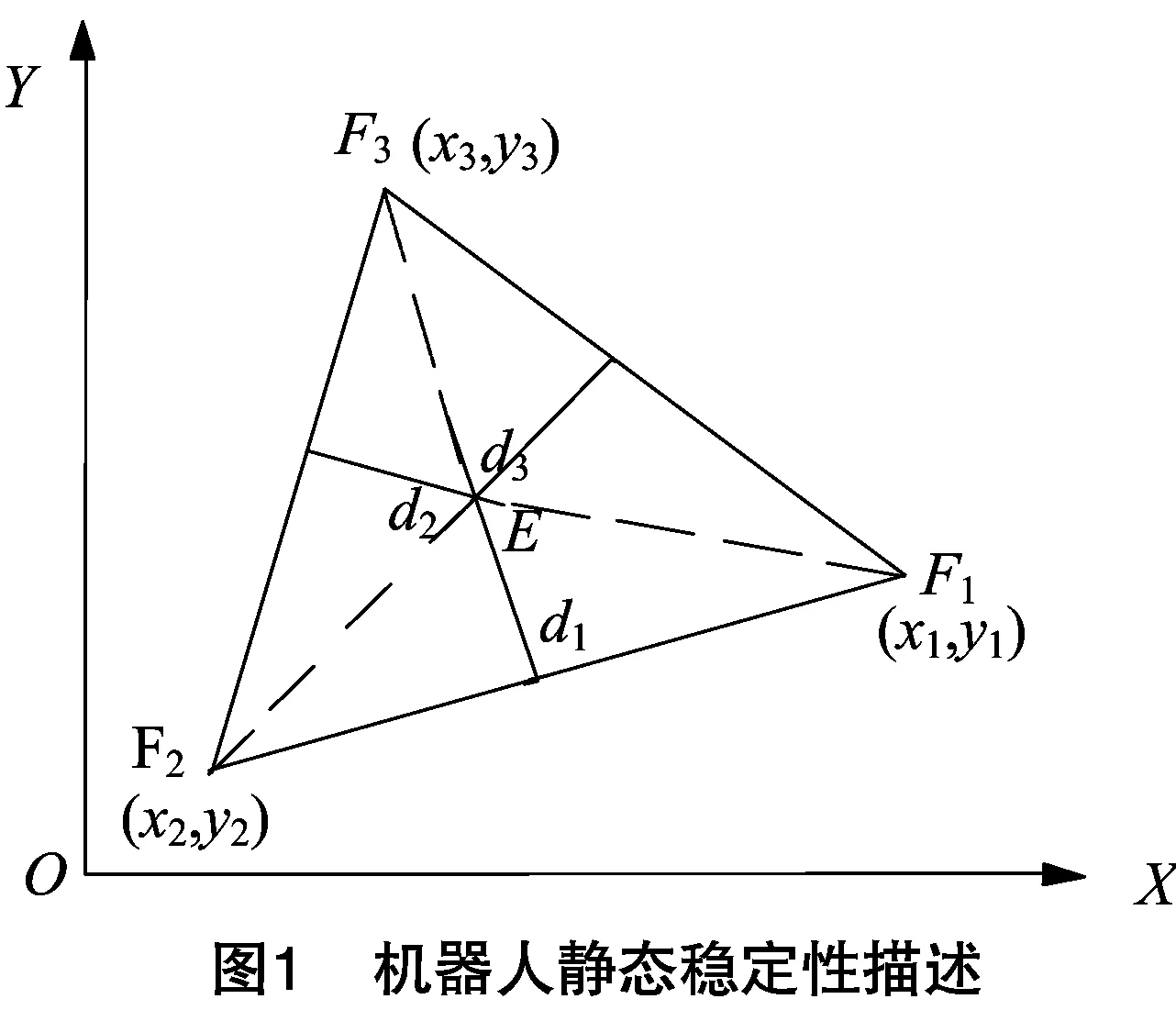
其中，三角形区域△F1F2F3表示机器人3个立足点F1、F2、F3围成的稳定区域，点E为机器人的重心。当点E位于这一区域时，机器人是静态稳定的。若某时刻重心及立足点在水平面(XY平面)的位置投影坐标分别是：E(x，y)、F1(x1，x2)、F2(x2，y2)、F3(x3，y3)。

S△EF1F2+S△EF2F3+S△EF1F3=S△EF1F2F3。

若上式成立，机器人处于静态稳定。机器人重心垂直投影到其立足点投影三角形各边的最小距离为其稳定裕度di(i=1，2，3)。机器人稳定裕度为：

dM=min{d1，d2，d3}。

若dM≥0，机器人是稳定的。根据稳定裕度可以分析机器人步行的静态稳定性。机体的运动和腿相对机体的运动在任何时刻必须是协调一致的，这样才能使机器人重心的垂直投影一直落在三足支撑点构成的三角形区域里面，从而实现稳定行走。

2.1.1 重心投影法 1968年，McGhee等提出了重心投影法(center of gravity projection method，简称CGPM)，把机器人各个腿与地面的接触点所构成的凸多边形作为一个稳定区域。当机器人重心的水平投影区域位于凸多边形内时，机器人处于静态稳定状态[5]。当Sm≥0时，重心落在水平投影平面内，则机器人是稳定的，重心投影法表示为：

Sm=min{Sm，f，Sm，r，Sm，s}

其中，Sm为稳定裕度；Sm，f、Sm，r、Sm，s分别为机器人重心的水平投影到支撑多边形前边界、后边界、两侧边界的绝对水平距离。

李军科等利用重心投影法，从偏心轮腿六足机器人的机身和三足步态的特点入手，分析了该机器人在使用三足步态行走时的特点，并论证了偏心轮腿六足机器人的三足步态具有静态稳定性的特点[6]。此法仅仅反映的是在平坦光滑地面上机器人的静态稳定性，对于机器人在不平坦地面上的稳定性难以评判。

2.1.2 静态稳定边界法 1979年，McGhee 等提出了静态稳定边界法(static stability margin，简称SSM)[7]。即基于质心与支撑多边形几何关系的判定方法，该方法只考虑机身位置和质心分布情况。静态稳定边界法主要是利用质心在支撑平面上的投影和支撑腿(机器人运动时，位于地面上的腿)所构成的多边形的位置关系来判断机器人的稳定状态[8]。支撑区域的水平投影是稳定区域，在该区域内，机器人的重心到各边界距离的最小值就是静态稳定裕量。付贵永等在此基础上为解决加速度和外力问题提出了纵向稳定边界法(longitudinal stability margin，简称LSM)，表示在支撑区域内将机器人重心投影到支撑区域前、后边界的较小纵向距离。它用机器人重心投影到支撑区域前后两支撑边界的稳定裕量来度量[9]。屈亮等针对稳定域内外的不同初始状态，进行了零输入响应时域仿真，验证了相平面法确定的稳定域的有效性和准确性，研究结果可为飞机结冰后的稳定边界确定和边界保护提供一定的参考[10]。而SSM是指质心沿重力方向在支撑平面上的投影到支撑多边形各边距离中的最小值。四足机器人在斜面上的情况如图2所示。

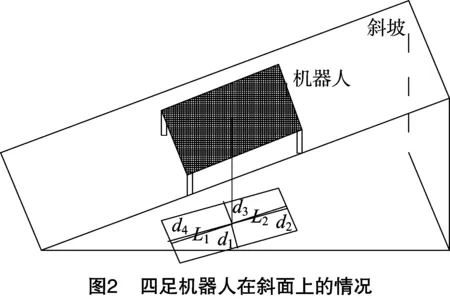
SSM法与LSM法度量的稳定裕量为：

SSM=min{d1，d2，d3，d4}；LSM=min(L1，L2)。

其中，机器人在斜坡上，其中心点向水平地面作投影。d1、d2、d3、d4分别为机器人的重心投影到机器人投影区域各边界的距离；L1、L2分别指重心投影到区域前后边界的较小纵向距离。但由于静态稳定边界法的不足是基于图形内的几何计算建立起来的，均未考虑势能大小等约束因素的影响，故在机器人上下坡行走时会发生倾覆[11]。

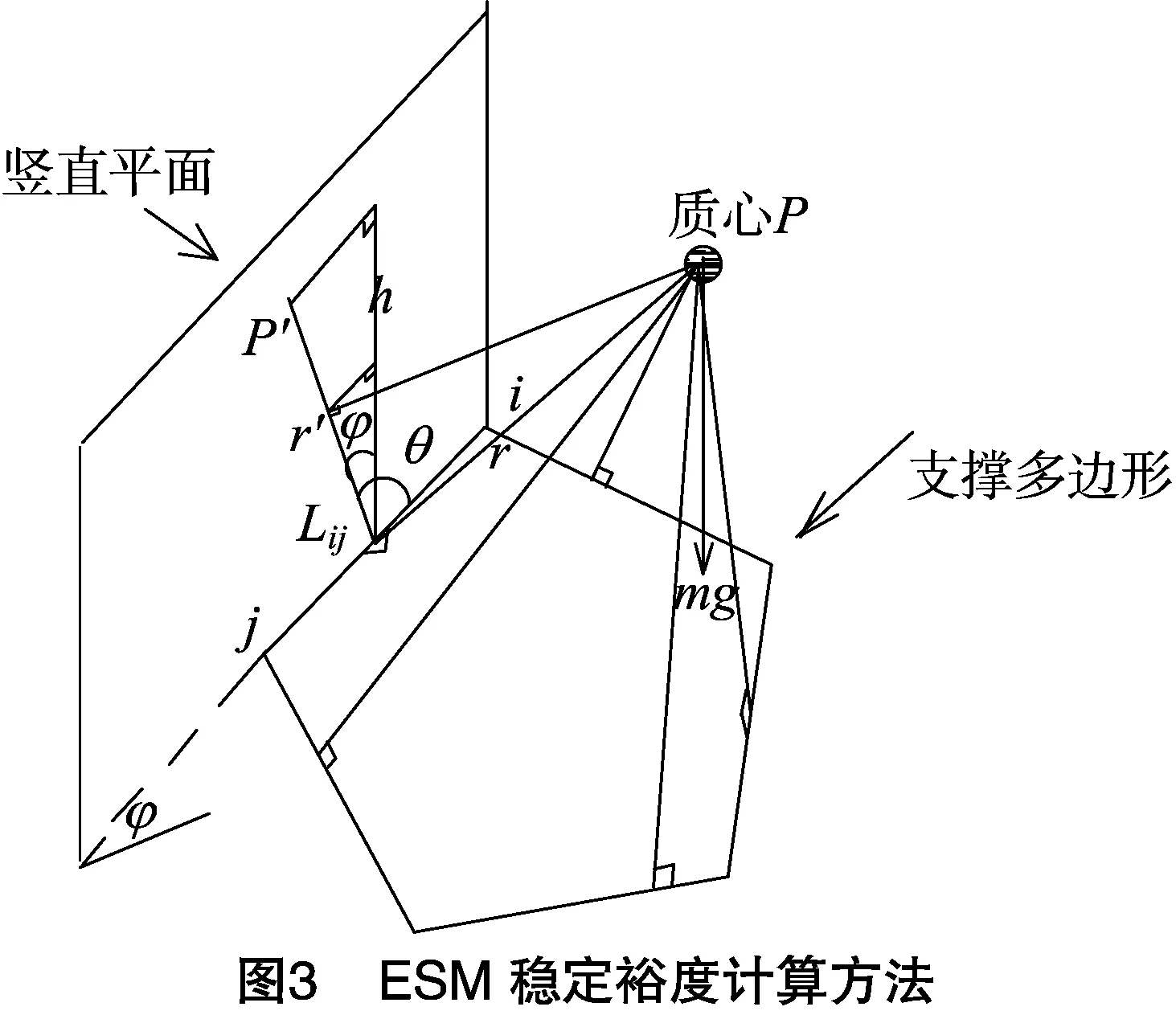
2.1.3 能量稳定边界法 能量稳定边界法(energy stability margin，简称ESM)是一种更为准确的描述机器人在不平坦地面上行走的稳定性判别方法。从能量角度看，能量稳定边界法是通过计算从当前状态到倾翻状态所须克服的最小势能来判定该状态稳定性的判别方法，主要描述机器人在不平坦地面上的稳定性判别方法[12]。稳定裕度计算方法如图3所示。从质心P作支撑多边形各边的垂线，从P点向竖直平面作垂线交于点r′，P点到lij的距离为r，从位置P沿轴lij旋转到竖直平面内交于点P′，r与P′r′的夹角为θ，lij上的垂线与P′r′的夹角为φ，当质心从位置P沿轴lij旋转到竖直平面内的P′点时，高度增加h，此过程中增加的势能即为ESM法对应于边lij的稳定裕度，分别计算各边对应的稳定裕度并取其中的最小值，即为机器人此时的稳定裕度值。在未考虑运动惯量的影响时，机器人不再受步行机械和支撑地形的约束[13]，沿支撑区域的任一边界发生倾覆所要求的最小势能稳定裕量为：

SESM=min(mghi)(i=1，2，…)。

其中，m是机器人的质量；g是重力加速度；i是支撑多边形被视为旋转轴的边；hi是机器人沿不同支撑边界翻转时的重心位置的增量。

hi=|ri|(1-cosθ)cosφ。

但该法不足之处是未考虑机器人自身质量的影响，为解决上述问题，在此基础上Hirose提出了规范化的能量稳定边界法(normalized energy stability margin，简称NESM)，其表达公式为：

式中：各项系数与ESM法中的表达相同。

朱翔宇通过对实际青蛙跳跃模型的观察，归纳影响跳跃稳定性的因素，分析造成跳跃失败的原因，运用能量稳定边界法提出了仿生机器人稳定着陆的判据，并对机器人跳跃的稳定性过程进行综合探讨，计算出机器人各阶段运动姿态，提出运动轨迹方程和获得方法，以及肢体末端位置的计算方法[14]，为进一步研究奠定了基础。

2.2 动态稳定性

机器人动态稳定性判据发展相对于静态稳定性判据较慢，且其方法均是基于静态稳定性判据基础。故在一定条件下，动态稳定性判据既可以判断机器人静态稳定性也可以判断其动态稳定性[15]。

2.2.1 零力矩点法 Vukobratovic在1968年提出零力矩点(zero moment point，简称ZMP)法，认为若地面上存在重力、外力和惯性力对该点的合力矩为0的点，该点称为零力矩点。如果ZMP在支撑区域内，则机器人是稳定的。ZMP又称为压力中心或地面反作用力中心，其地面反作用力关于该点的力矩只有垂直分量，沿水平面内的2个垂直轴方向的分量为0。ZMP判定方法如图4所示。

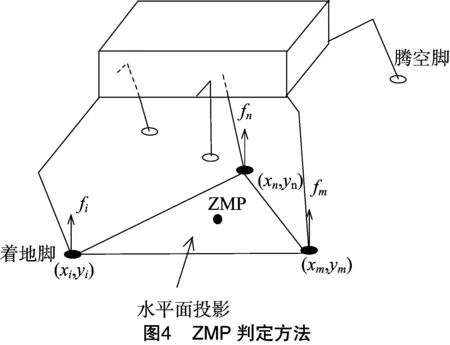
以六足机器人为例，可假设当其中3个脚在地面上时，其他脚腾空，着地脚所组成的三角形为水平面投影区域。设零力矩点水平投影中的一点的坐标为ZMP(x，y)，i、m、n号着地脚坐标分别为(xi，yi)、(xm，ym)(xn，yn)，fi、fm、fn分别为第i、m、n号着地脚在竖直方向上的足力分量。

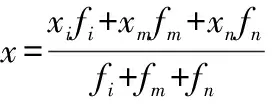
ZMP点到支撑多边形的最小距离即为此时刻机器人的ZMP稳定裕度。ZMP落在脚掌的范围里，机器人可稳定行走。徐兆红等讨论了腿式机器人稳定性控制与稳定性判定准则，基于稳定约束条件零力矩点，提出一种干扰下的动态稳定性控制方法[16]。Zhu等利用ZMP法得到了双足机器人行走的步态特性[17]。沈继红等在ZMP法的基础上从地面反力和能量的角度在理论上讨论了机器人脚跟高度对其行走稳定性的影响，证明了适当增加足式机器人的脚跟高度可增强其步行稳定性[18]。

2.2.2 压力中心法 1976年，Orin 提出了压力中心法(center of pressure，简称COP)，一种基于合外力与支撑多边形几何关系的判定方法。该方法计算质心沿合力方向到支撑平面的投影，如果该投影在支撑平面多边形内，则处于稳定状态。他认为在机器人单脚与地面接触时，如果脚掌受到的压力与作用于某一点的合外力相等，而且在该点平行于脚掌方向上的合力矩为零，则该点称为COP点[19]。当COP点在与地面接触脚掌区域的内部时，机器人处于稳定状态。COP的结构如图5所示，F为质心处的合外力，O是质心，O沿F方向在支撑平面内的投影点为C，A3A4的长度是a34，点C到A3A4的距离为da34，O到A3A4的距离为L34，θbij为F与O到支撑多边形边线的垂线Lij间的夹角，θdi为F与质心O到着地脚点Ai连线Pi间的夹角。夹角愈大，机器人的稳定裕度愈大。点C到支撑多边形各边距离中的最小值即为COP稳定裕度。

SCOP=min(doij)(i，j=1，2，…)。

其中，doij为质心O投影点到支撑多边形各边线的距离。

王鹏飞等为准确评定足式机器人的行走稳定性及稳定裕度，运用压力中心法提出了采用支撑面压力中心至机器人各足支撑点构成的支撑多边形各边的最短距离来评定机器人的行走稳定性的一般准则[20]。根据压力中心的坐标关系，将压力中心位置转化为重心坐标表达式，通过重心到支撑多边形边缘的最短距离来间接判定机器人的稳定性。

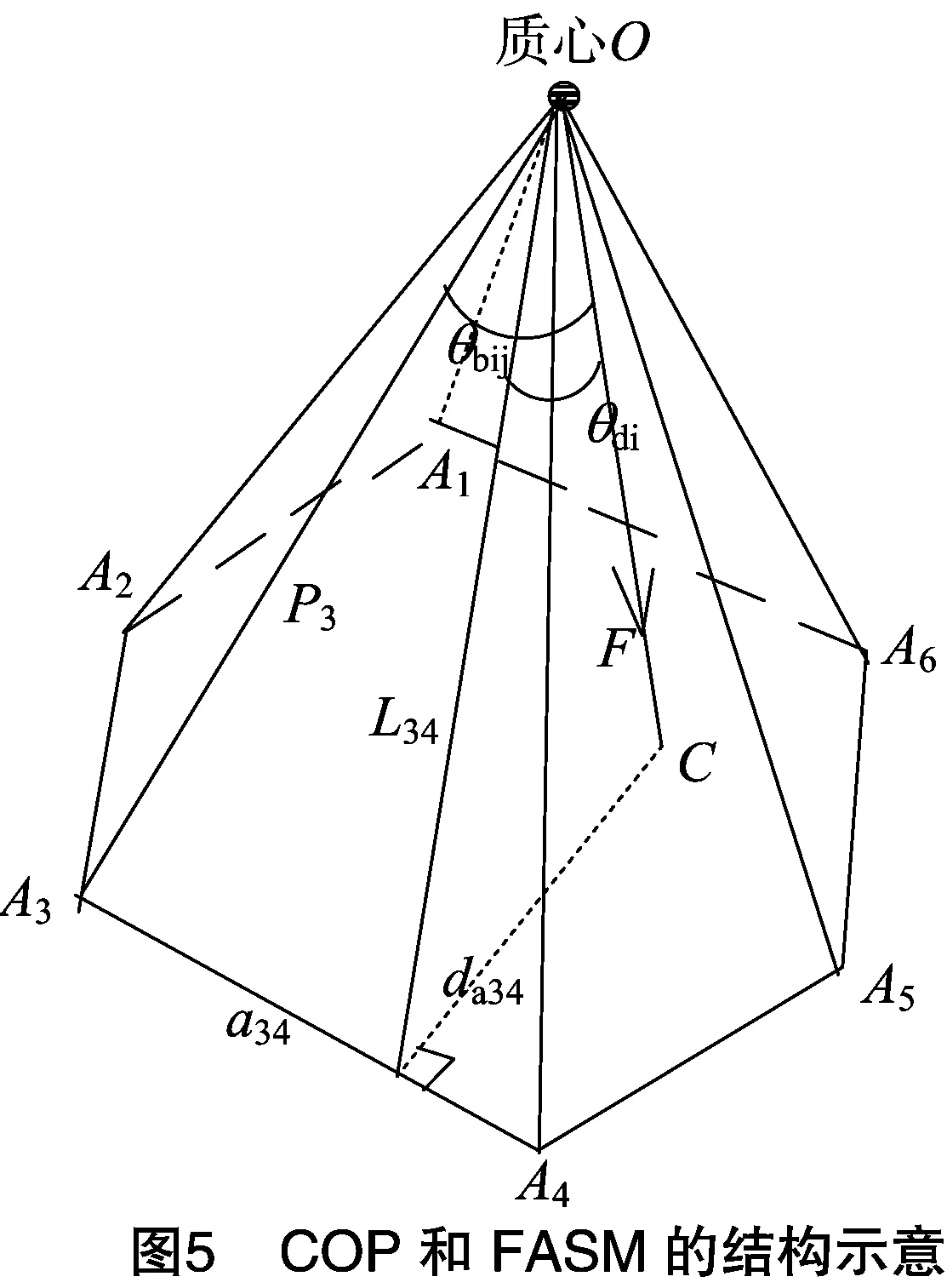
2.2.3 力-角法 力-角法(force-angle stability margin，简称FASM)是Papadopoulos等提出的一种基于合外力与支撑多边形几何关系的判定方法，是计算质心位置处所受合外力和质心到稳定锥各边线垂线间的夹角以及合外力和质心到各着地脚点连线间的夹角中的最小值[21]。由图5可知，θbij为合外力F与质心O到支撑多边形边线的垂线Lij间的夹角，θdi为合外力F与质心O到着地脚点Ai连线Pi间的夹角。稳定裕度随夹角的增大而增大。此法优点是能分析多种稳定裕度。FASM的计算方法如下：

SFASM=min(θbij，θdi)(i，j=1，2，…)。

刘娟秀等为研究机器人的倾翻稳定性，针对一种新型轮足式爬楼梯机器人，提出了考虑爬楼梯机器人具有人机交互的特殊性，将地形和人体坐姿对机器人的影响等效为干扰力和干扰力矩，结合力-角法等计算机器人的动态稳定性指数[22]，为机器人稳定性的进一步研究奠定了基础。

2.2.4 庞加莱映射-李雅普诺夫判据法 庞加莱映射是指系统运动的状态空间轨迹与其庞加莱截面2个连续交点处的状态变量之间的映射。庞加莱对连续运动的轨迹用一个截面(即庞加莱截面)将其横截，根据轨迹在截面上的穿过情况，可清晰判断运动的形态，由此所得的图像叫庞加莱映像[23]。庞加莱映射函数是反映由系统的运动方程所决定的状态变化轨迹，从庞加莱截面一点的状态演变到轨迹与庞加莱截面下个交点的状态。李雅普洛夫方法，可用来描述一个动力系统的稳定性。Koditschek等采用相位和庞加莱映像法分析Raibert的单腿跳跃机器人的稳定性，为对机器人稳定性的进一步研究提供了依据[24]。

如果此动力系统任何初始条件在平衡态附近的轨迹均能维持在平衡态附近，那该系统可以称为在该处李雅普诺夫稳定，也可指通过系统微分方程解的性质进行稳定性判别的方法[25]。它不须要求解微分方程即可判断系统的稳定性，但它通常无法提供有关瞬时响应或系统性能的信息，因而此理论的普遍适用性未达到期望，仍须进一步研究来判别系统稳定性，但对于非线性复杂系统必须进行线性化处理。

3 稳定性判据应用场景分析

由表1可知，对基于质心与支撑多边形几何关系的静态稳定边界法和纵向稳定边界法等2种判定方法，均适用于坡地；对于能量稳定判据法，在不平坦的地面更加稳定；而对于重心投影法和规范化的能量稳定边界法，只能作为平坦光滑地面上机器人的静态稳定性判别指标，而对于在不平坦的工作环境中运行的机器人，该方法则不适用于稳定性的判别。

表1 静态稳定性判据应用场景

注：平地是指平坦的地面；坡地是相对于平地来说，崎岖不平复杂且有一定倾斜的地面。下表同。

由表2可知，对于力-角法和零力矩点法，在平坦和不平坦的地面上都可以作为机器人的静态稳定性判别指标。其他方法目前还未探索出具体的使用场景。

表2 动态稳定性判据应用场景

注：“*”表示还没有明确适合的场景。

4 结论

目前机器人的稳定性理论研究均已取得较大进展，重心投影法、规范化的稳定边界法适用于平地；静态稳定边界法、纵向稳定边界法和能量稳定边界法适用于坡地；零力矩点法和力-角法既适用于平地又适用于坡地，还有一些方法依据有待完善。随着机器人的应用越来越广泛，对其稳定性运用要求越来越高，这就决定了对机器人稳定性的研究必将更深入发展。

[1]王立权，王海龙，陈 曦，等. 八足仿蟹机器人行走稳定性分析[J]. 中南大学学报(自然科学版)，2014，45(10)：3416-3422.

[2]宣奇波，张怀相，戴国骏. 四足步行机器人稳定性步态规划[J]. 杭州电子科技大学学报，2013，33(2)：33-36.

[3]Jun J Y，Saut J P，Benamar F. Pose estimation-based path planning for a tracked mobile robot traversing uneven terrains[J]. Robotics and Autonomous Systems，2016，75：325-339.

[4]Wang L W，Du W L，Mu X Q，et al. A geometric approach to solving the stable workspace of quadruped bionic robot with hand-foot-integrated function[J]. Robotics and Computer-Integrated Manufacturing，2016，37：68-78.

[5]柳天虹，姜树海. 仿生六足机器人稳定性分析与仿真[J]. 计算机仿真，2013，30(12)：360-364.

[6]李君科，王宇俊，万 婷，等. 偏心轮腿六足机器人三足步态的静态稳定性分析[J]. 河南教育学院学报(自然科学版)，2012，21(1)：40-43.

[7]McGhee R B，Iswandhi G I. Adaptive locomotion of a multilegged robot over rough terrain[J]. IEEE Transactions On Systems，Man，And Cybernetics，1979，9(4)：176-182.

[8]Migdalovici M，Vlădăreanu L，Baran D，et al. Stability analysis of the walking robots motion[J]. Procedia Computer Science，2015，65(9)：233-240.

[9]付贵永，周利坤. 机器人稳定性研究综述和展望[J]. 机械工程与自动化，2013(2)：215-217.

[10]屈 亮，李颖辉，袁国强，等. 基于相平面法的结冰飞机纵向非线性稳定域分析[J]. 航空学报，2016，37(3)：865-872.

[11]Kim H G，Lee D G，Seo T W. Rolling stability enhancement via balancing tail for a water-running robot[J]. Journal of Bionic Engineering，2015，12(3)：395-405.

[12]McGhee R B，Frank A A. On the stability properties of quadruped creeping gaits[J]. Mathematical Biosciences，1968，3：331-351.

[13]王良文，李安生，唐维纲，等. 具有手脚融合功能的四足步行机器人的工作空间研究[J]. 高技术通讯，2014，24(1)：72-79.

[14]朱翔宇. 仿青蛙跳跃机器人稳定跳跃的研究[D]. 哈尔滨：哈尔滨工业大学，2011.

[15]王立权，王海龙，陈 曦，等. 仿蟹机器人行走稳定性判定方法[J]. 高技术通讯，2013，23(2)：167-173.

[16]徐兆红，喻洪流，闫士举，等. 基于加速度映射的跳跃机器人稳定性控制[J]. 控制工程，2012，19(2)：262-264.

[17]Zhu H B，Luo M Z，Mei T，et al. Energy-efficient bio-inspired gait planning and control for biped robot based on human locomotion analysis[J]. Journal of Bionic Engineering，2016，13(2)：271-282.

[18]沈继红，丁二华. 一种类人型机器人的步行稳定性研究[J]. 哈尔滨工程大学学报，2004，25(4)：536-539.

[19]于苏洋，王 挺，王志东，等. 基于倾翻与滑移稳定性准则的轮椅机器人爬楼梯控制方法[J]. 仪器仪表学报，2014，35(3)：676-684.

[20]王鹏飞，黄 博，孙立宁. 四足仿生机器人稳定性判定方法[J]. 哈尔滨工业大学学报，2008，40(7)：1063-1066.

[21]田海波，方宗德，周 勇，等. 轮腿式机器人倾覆稳定性分析与控制[J]. 机器人，2009，3l(2)：159-165.

[22]刘娟秀，吴益飞，郭 健，等. 一种轮足式爬楼梯机器人的倾翻稳定性研究[J]. 南京理工大学学报(自然科学版)，2015，39(6)：643-649.

[23]张奇志，周亚丽. 基于脉冲推力作用的双足机器人半被动行走[J]. 东南大学学报(自然科学版)，2013，43(增刊1)：102-106.

[24]Koditschek D E，Bühler M. Analysis of a simplified hopping robot[J]. The International Journal of Robotics Research，1991，10(6)：587-605.

[25]Zhang X Z，Liu X Y，Liu Y X，et al. Influence of the swing ankle angle on walking stability for a passive dynamic walking robot with flat feet[J]. Advances in Mechanical Engineering，2016，8(3)：1-13.