二维时间域黏声波全波形反演
2018-03-10李海山杨午阳雍学善
李海山 杨午阳 雍学善
(①中国石油勘探开发研究院西北分院,甘肃兰州 730020; ②CNPC油藏描述重点实验室,甘肃兰州 730020)
1 问题的提出
理想地球介质为弹性介质,而实际地球介质具有黏滞性,导致地震波在地层中传播出现能量衰减、频带变窄、主频降低、相位延迟等现象[1-3],尤其对于近地表强衰减层或者是地下含气层等强衰减区域,如果不考虑这些介质的黏滞性,采用声波方程正演模拟得到的地震波场与实际观测波场之间的差异较大,造成全波形反演得到的介质参数与实际介质参数之间产生较大误差[4,5]。因此,研究地震波在黏弹性介质中传播规律并探讨黏弹性介质全波形反演方法具有重要意义。
通过对黏弹性介质衰减机理及衰减规律的研究,人们提出了多种黏弹性模型,如广义Maxwell体模型[6]、广义Zener体模型[7]、Futterman模型[8]、广义Kelvin-Voigt模型[9]、Kjartansson模型[10]、广义准线性固体(generalized standard linear solid,GSLS)模型[11]等。不同的黏弹性模型,其相应的波动方程也不同,如位移、位移—应力、位移—速度—应力和速度—应力等不同形式的方程[12]; 波动方程类型不同,则其相应数值模拟方法也不同,实现的难易程度和计算量也不同。同时,研究表明地球介质在地震频带范围内具有近似常Q特征[2],即地下介质品质因子在地震频带范围内基本不随频率发生变化,而GSLS模型(图1)可很好地近似这种常Q特征[13];此外,GSLS模型相应的波动方程具有在时间域易于数值求解的优点。因此,基于GSLS模型的黏弹性或黏声波方程正被越来越多地应用于正演模拟、逆时偏移及全波形反演等领域[14-19]。
Bai等[4,18]基于单个Maxwell体构成的GSLS模型,采用二阶黏声波方程实现了时间域黏声波全波形反演方法并进行实际资料的全波形反演。研究表明由单个Maxwell体构成的GSLS模型不足以近似地球介质在地震频带范围内的常Q特征,为了更好地近似地球介质在地震频带范围内的常Q特征,应该采用由多个Maxwell体构成的GSLS模型[13],同时二阶黏声波方程不便于采用高阶交错网格差分法求解。本文从Bohlen[20]基于GSLS模型得到的一阶速度—应力黏弹性波方程出发,得到一阶速度—应力黏声波方程,并推导出相应的速度梯度计算公式,同时采用共轭梯度法和高阶交错网格有限差分法,实现了二维时间域黏声波方程全波形反演方法,并通过模型测试验证了该方法的有效性。
2 一阶速度—应力黏声波方程
Bohlen[20]基于GSLS模型(图1)得到各向同性介质中的一阶速度—应力黏弹性波动方程,并进行三维黏弹性波正演模拟方法研究。考虑到理想声介质中不存在剪切应力,则由一阶速度—应力黏弹性波动方程可得到如下的一阶速度—应力黏声波方程
(1)
式中:p为压力场;vi为波场速度分量;ρ为介质密度;fp为震源项;L为GSLS模型中Maxwell体的个数;rl和τσl分别为第l个Maxwell体对应的记忆变量和应力松弛时间;τp为纵波松弛时间;M为松弛模量,且有
(2)
其中:符号R()表示取实部;ω0为参考频率。若品质因子Q已知,则可利用Blanch等[13]或Bohlen[20]给出的方法计算出最优应力松弛时间τσl和纵波松弛时间τp。式(1)相应的应力—位移黏声波波动方程为
(3)
式中ui为波场位移分量。若设置Maxwell体的个数为1,则该式就转化为Bai等[4]采用的二阶黏声波方程。
3 目标函数及模型参数梯度
全波形反演是利用全波场信息,通过一定的优化方法估计地下介质参数模型,使正演地震记录与观测地震记录达到最佳拟合[21]。设目标函数为波场残差能量,即
(4)
式中δu=u-uobs,u=(vx,vz,p,rl)T为地震波场向量。目标函数对模型参数求偏导,有
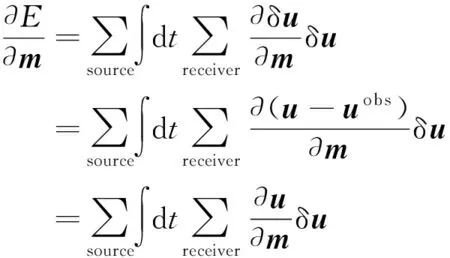
(5)
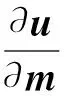
(6)
同理可由数据空间小的扰动得到模型空间总的变化[22]
(7)
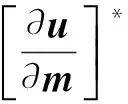
(8)
(9)
可见目标函数对模型参数的梯度等于由数据空间小的扰动引起的模型空间的变化量。如果在式(3)中的各变量和参数都施加一阶扰动,同时把模型参数变化引起的数据空间的扰动看作是新的震源,结合式(6)~式(9)推导可得松弛模量的梯度计算公式(详细推导见附录A)。松弛模量的梯度为
(10)
式中pford和pback分别为正演模拟压力场与残差逆时反传压力场。据式(2)纵波速度与松弛模量之间的关系,可得到纵波速度梯度
(11)
4 全波形反演策略
要使目标函数达到最小,目前基本上都采用局部优化方法。在局部最优化方法中,虽然共轭梯度法只利用一阶导数信息,却克服了最速下降法收敛慢的缺点,避免了牛顿法需要存储和计算Hessian矩阵并求逆的缺点,因此得到广泛的应用[23,24]。本文采用共轭梯度法更新纵波速度模型,即
vP,n+1=vP,n+αφn
(12)
式中:n为迭代次数;α为更新步长;φn为共轭方向
(13)
通过FR方法[22],可计算得到
(14)
反演过程中采用固定步长,保持Q模型和密度参数不变;在每次迭代过程中,正演波场和残差逆时反传波场用式(1)计算得到,用式(11)计算纵波速度梯度,波场计算采用8阶交错网格有限差分法;为更好地近似常Q特征,设置GSLS模型中Maxwell体的个数为3[1]; 给定GSLS模型参数τσl,可利用Blanch等[13]给出的方法得到给定频带范围内的最优纵波松弛时间τp。此外,若在全波形反演过程中令式(1)中的记忆变量及与黏弹性相关的参数为零,即可进行二维声波全波形反演。
5 方法模型测试
图2a是从3D SEG/EAGE逆掩推覆模型中抽取出来的一个二维速度模型,网格尺寸为400m×187m,空间步长为12m; 图2b是对图2a进行平滑后得到的,作为全波形反演的初始速度模型; 图2c是由图2a所示速度模型映射后生成的Q模型;图2d是对图2c进行平滑而生成的平滑Q模型。Q模型在近地表衰减最强,从浅到深衰减逐渐减弱。
利用图2a所示速度模型和图2c所示Q模型生成二维黏声波观测记录,震源子波选取主频为15Hz的雷克子波,炮点与接收点均置于距地面24m位置处,共采集80炮,每炮设置400个检波点,炮间距为60m,检波点距为12m,记录长度为1.5s,时间采样间隔为1ms,图3b是其第40个单炮记录。采用相同参数,利用图2a所示速度模型生成二维声波观测记录,图3a是对应的第40个单炮记录。与声波炮记录比较可见,黏声波炮记录随旅行时增加能量快速衰减,到深层已看不到弱反射信息。
图4给出了图3中两个矩形区域正演炮记录相应的振幅谱,其中蓝线对应声波正演炮记录,红线对应黏声波正演炮记录,明显可见地震波的衰减随着旅行时的增大而增强,同时可见地震波的主频随着旅行时的增大而降低。
首先,以声波正演炮记录为观测记录,从图2b所示初始速度模型出发进行声波全波形反演,迭代50次后得到图5a所示的纵波速度反演结果。然后,以黏声波正演炮记录为观测记录,分别进行声波及黏声波全波形反演,迭代50次后得到图5b和图5c所示的纵波速度反演结果,黏声波全波形反演过程中采用图2c所示的真实Q模型。由图5a可见,对于声波观测记录,采用声波全波形反演方法会得到较好反演结果,而由图5b和图5c可见,对于黏声波观测记录,采用声波全波形反演方法会得到错误结果,反演得到纵波速度模型偏离真实纵波速度模型较远,只有采用黏声波全波形反演方法才会得到较准确反演结果。
在进行实际资料全波形反演时,准确的Q模型是得不到的,只能得到相对准确的平滑Q模型,为研究本文反演方法对Q模型的敏感性,以黏声波正演炮记录为观测记录,采用图2d所示的平滑Q模型进行黏声波全波形反演,反演结果见图5d。比较图2c和图2d可见虽然平滑Q模型与真实Q模型有一定的偏差,但比较图5c与图5d可见采用平滑Q模型能够得到与采用真实Q模型接近相同的反演结果,这表明在进行实际资料全波形反演时,只要提供足够准确的平滑Q模型,就能显著提高反演结果的准确性。

图3 第40炮正演记录 (a)声波炮记录; (b)黏声波炮记录
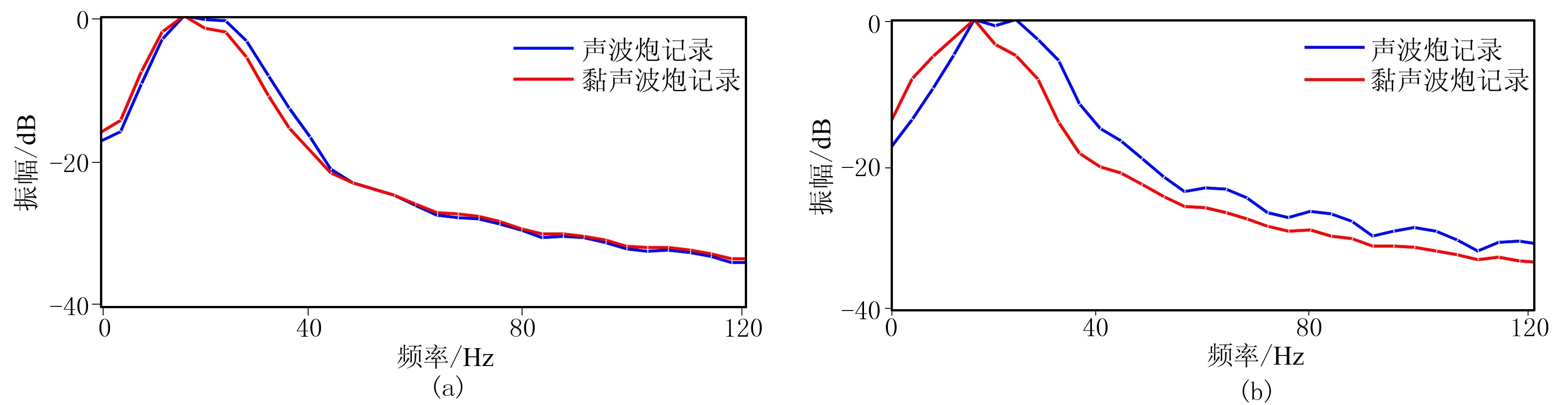
图4 对应图3中两个矩形区域炮记录的振幅谱 (a)蓝色矩形框; (b)红色矩形区域
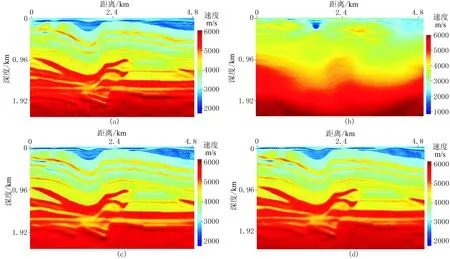
图5 全波形反演迭代50次得到的纵波速度模型 (a)声波观测—声波全波形反演; (b)黏声波观测—声波全波形反演; (c)黏声波观测— 黏声波全波形反演—真实Q模型; (d)黏声波观测—黏声波全波形反演—平滑Q模型
图6a和图6b分别为模型水平方向1.8km和3.0km位置处以黏声波正演炮记录为观测记录,反演前、后的单道速度曲线比较,可更明显地看出黏声波反演结果较接近真实模型,而声波全波形反演结果误差较大,且深度越大偏离真实模型越远。
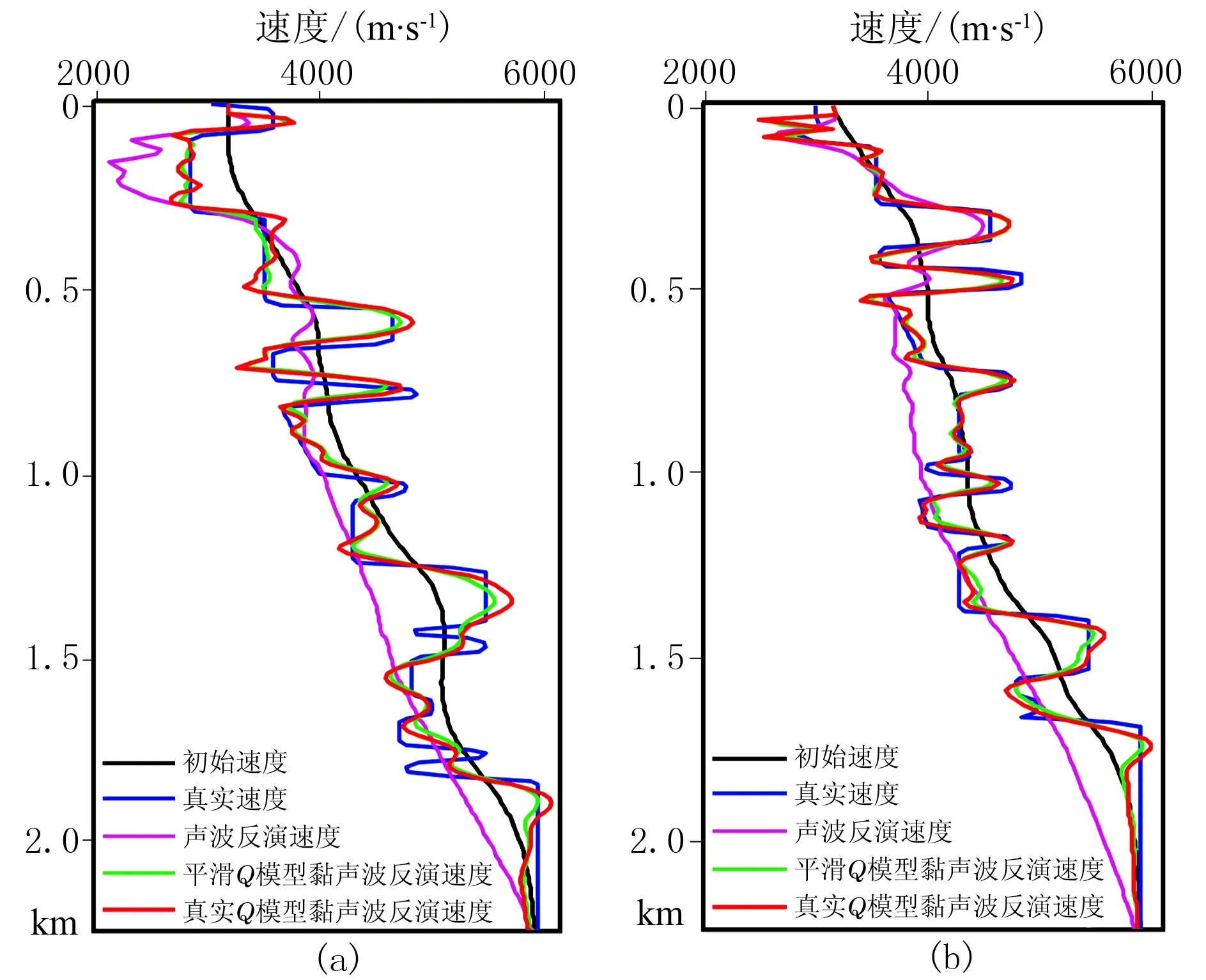
图6 真实模型及反演纵波速度单道曲线比较 (a)1.8km位置速度曲线; (b)3.0km位置速度曲线
图7是以黏声波正演炮记录为观测记录,进行全波形反演时归一化数据残差随迭代次数的变化曲线,由图可见声波全波形反演方法和黏声波反演方法都收敛了,但声波全波形反演方法得到了错误的反演结果,而黏声波全波形反演方法得到的反演结果是正确的,迭代50次后观测记录与拟合记录之间的误差较小。因此,全波形反演中,反演误差和收敛曲线只可作为一种参考,不能作为衡量反演结果准确性的标准。
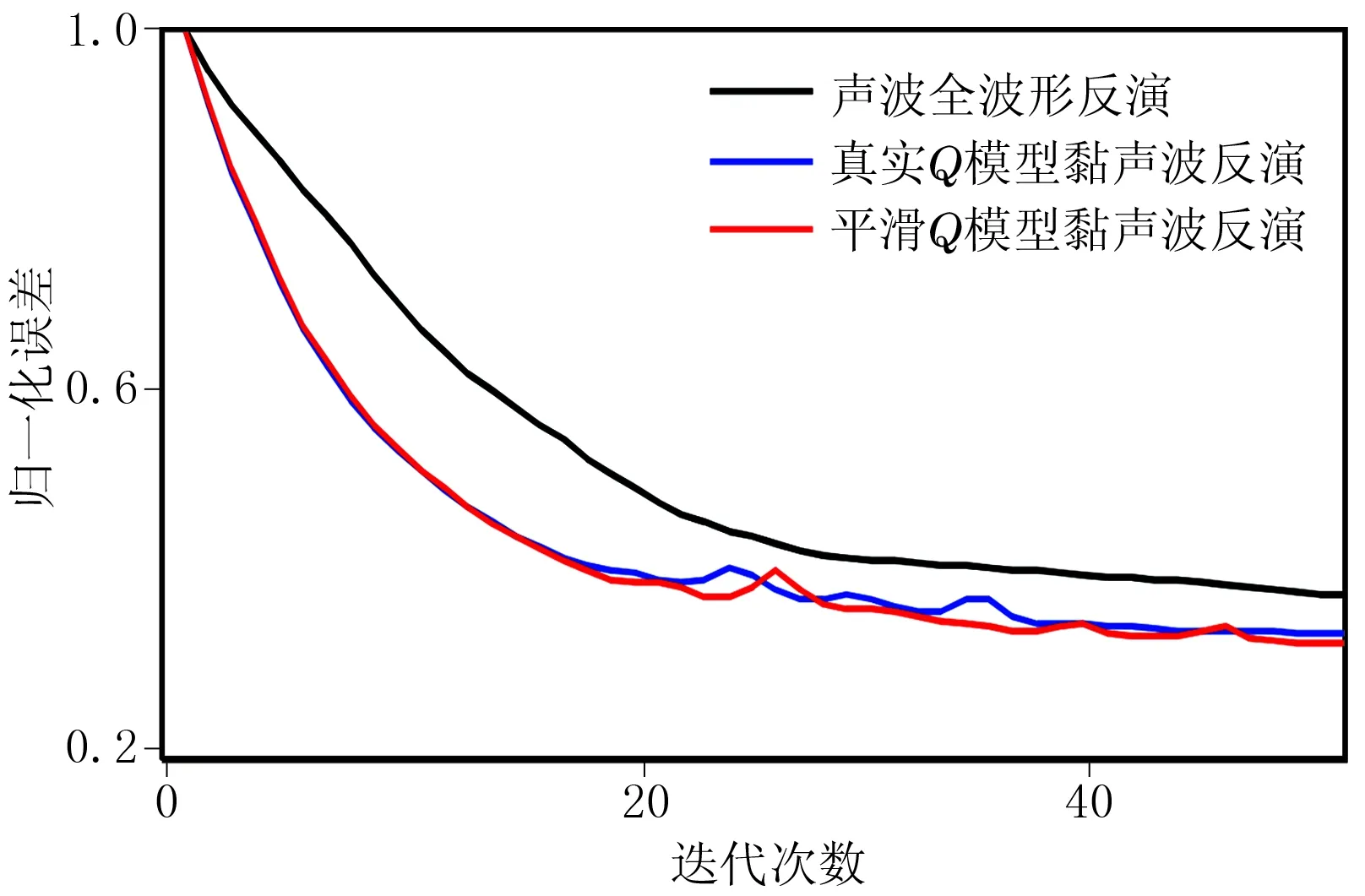
图7 归一化误差随迭代次数变化曲线
考虑到实际资料全波形反演中噪声干扰是不可避免的,对于陆上资料该问题尤为严重,为分析随机噪声对本文反演方法的影响,在黏声波观测记录中加入信噪比为10的随机噪声(图8a),采用图2d所示的平滑Q模型进行黏声波全波形反演(图9)。比较图3b与图8b可见,观测炮记录与反演炮记录中反射同相轴的旅行时和波形匹配较好;同时,比较图2a与图9可见,当观测记录中含有一定信噪比的随机噪声时,也能得到相对较好的纵波速度反演结果。
需要注意的是,本文在反演过程中采用的子波是准确子波,反演方法的噪声抑制能力也有待进一步提高,为进一步提高反演方法的性能,下一步可采用褶积型目标函数[25],并引入模型参数的正则化项[26]。

图8 含噪黏声波炮记录(a)及其全波形反演炮记录(b)
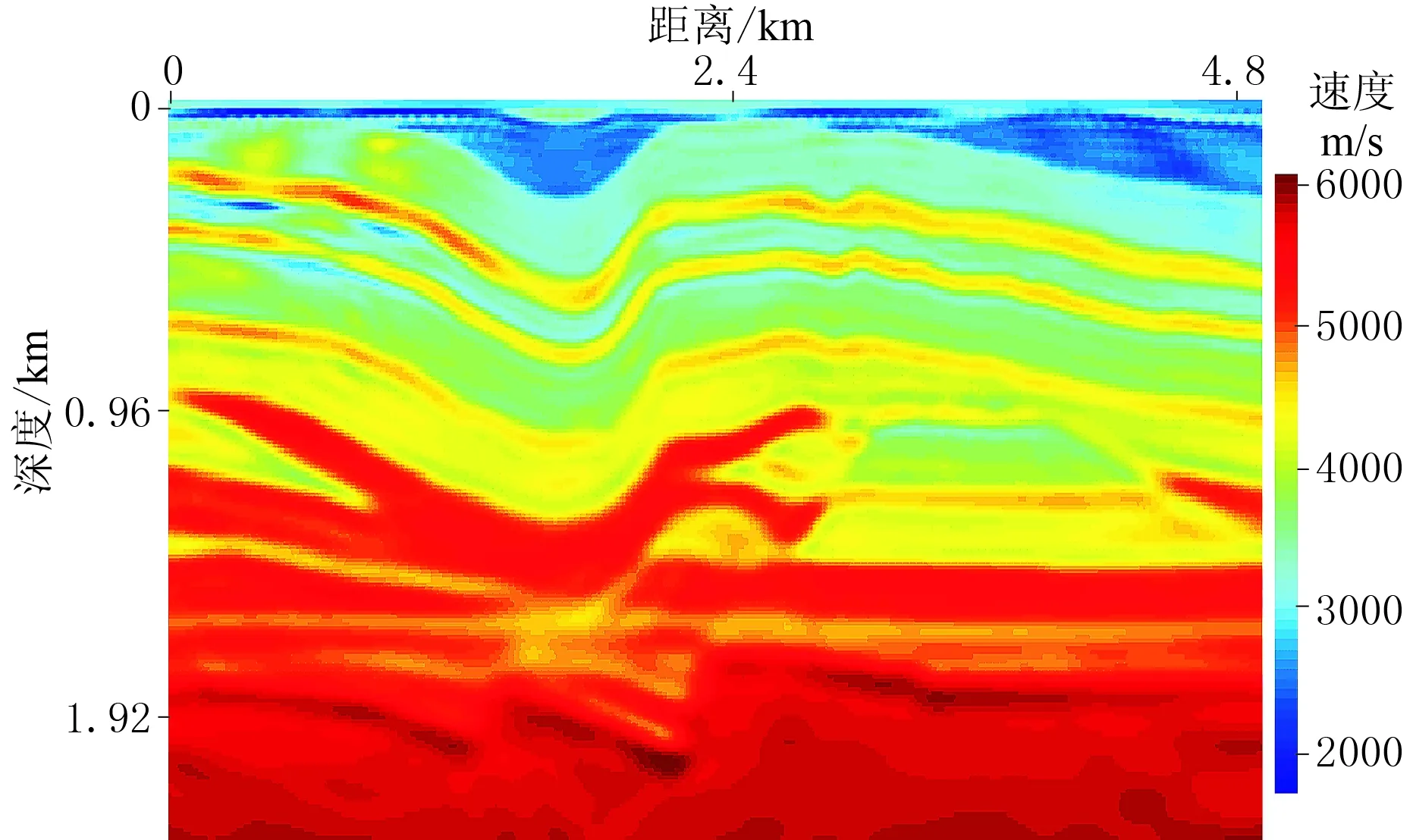
图9 含噪黏声波炮记录黏声波反演结果
6 结论
本文采用基于GSLS黏弹性模型的二维一阶速度—应力黏声波方程,推导出相应的纵波速度梯度计算公式,并采用高阶交错网格有限差分法和共轭梯度法,实现了二维时间黏声波全波形反演方法。该方法由于采用由多个Maxwell体构成的GSLS模型,可以更好地近似地球介质的常Q特征;由于在时间域实现,因此波场正演和残差逆时反传比较直接快速。
模型测试结果验证了该方法的可行性和有效性。以黏声波正演炮记录为观测记录时,与声波全波形反演结果相比,采用黏声波全波形反演方法能够得到较为准确的纵波速度反演结果,可见黏弹性对全波形反演结果的准确性和分辨率有较大的影响,因此建议在强衰减区域采用黏弹性或者黏声波全波形反演方法。
附录A 松弛模量梯度的推导
根据摄动理论,正文式(3)中的各波场变量和模型参数都施加一阶扰动,即
(A-1)
则可得到新的应力—位移黏声波方程
(A-2)
式中新的震源项
(A-3)
如果把模型参数变化引起的扰动看作是新的震源,则式(A-2)中位移变量δui的解为
δui(x,t)
(A-4)
式中Gi(x,t;x′,t′)为格林函数。如果令密度为常数,即只进行纵波速度的全波形反演,则ΔF=0,将式(A-3)代入式(A-4),有
(A-5)
对比式(6)可得
(A-6)
由式(7)可得
(A-7)
进一步整理,有
(A-8)
定义新的波场
(A-9)
则式(A-8)可写为
(A-10)
式中波场ψi(x,t)是由波场残差δu′在接收点位置开始逆时反传产生的。将式(A-10)中的隐式和展开,有
(A-11)
对于二维情形有
(A-12)
考虑到黏声波波场正演模拟和残差波场逆时反传都采用一阶速度—应力黏声波方程,所以式(A-12)中的位移分量需要用应力来替换。利用应力与位移关系式可得
(A-13)
式中pford和pback分别为正演模拟压力场与残差逆时反传压力场。
[1] Robertsson J O A,Blanch J O and Symes W W.Viscoelastic finite-difference modeling.Geophysics,1994,59(9):1444-1456.
[2] Liu H P,Anderson D L and Kanamori H.Velocity dispersion due to an elasticity;implications for seismology and mantle composition.Geophysical Journal International,1976,47(1):41-58.
[3] 陈志德,赵忠华,王成.黏滞声学介质地震波吸收补偿叠前时间偏移方法.石油地球物理勘探,2016,51(2):325-333. Chen Zhide,Zhao Zhonghua,Wang Cheng. Prestack time migration with compensation for absorption of viscous-elastic media.OGP,2016,51(2):325-333.
[4] Bai J,Yingst D,Bloor R et al.Waveform inversion with attenuation.SEG Technical Program Expanded Abstracts,2012,31:1-5.
[5] 杨午阳,王西文,雍学善等.地震全波形反演方法研究综述.地球物理学进展,2013,28(2):766-776. Yang Wuyang,Wang Xiwen,Yong Xueshan et al.The review of seismic full waveform inversion method.Progress in Geophysics,2013,28(2):766-776.
[6] Emmerich H and Korn M.Incorporation of attenuation into time domain computations of seismic wave fields.Geophysics,1987,52(9):1252-1264.
[7] Schiessel H,Metzler R,Biumen A et al.Generalized viscoelastic models:their fractional equations with solutions.Journal of Physics A: Mathematical and General,1995,28(23):6567-6584.
[8] Futterman W I.Dispersive body waves.Journal of Geophysical Research,1962,67(13):5279-5291.
[9] Jiang F and Mehta A J.Mudbanks of the Southwest Coast of India Ⅳ: Mud viscoelastic properties.Journal of Coastal Research,1995,11(3):918-926.
[10] Kjartansson E.Constant-Q wave propagation and attenuation.Journal of Geophysical Research,1979,84(B9):4737-4748.
[11] Carcione J M,Kosloff D and Kosloff R.Wave propagation simulation in a linear viscoacoustic medium.Geophysical Journal International,1988,93(2):393-407.
[12] Cao D.Viscoelastic wave equations based on different rheological model in time domain modeling.Beijing 2014 International Geophysical Conference & Exposition,2014,673-676.
[13] Blanch J O,Robertsson J O A and Symes W W.Mode-ling of a constant Q:Methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique.Geophysics,1995,60(1):176-184.
[14] Groos L,Schäfer M,Forbriger T et al.On the significance of viscoelasticity in a 2D full waveform inversion of shallow seismic surface.74th EAGE Conference & Exhibition Incorporating SPE EUROPEC 2012,Copenhagen,Denmark,2012.
[15] Zhang G and Gao J.Applying the t-method to visco-elastic forward modeling.SEG Technical Program Expanded Abstracts,2013,32:3531-3536.
[16] Dutta G,Lu K,Wang X et al.Attenuation compensation in least-squares reverse time migration using the visco-acoustic wave equation.SEG Technical Program Expanded Abstracts,2013,32:3723-3725.
[17] Bai J and Yingst D.Q estimation through waveform inversion.75th EAGE Conference & Exhibition incorporating SPE EUROPEC 2013,London,UK,2013.
[18] Bai J,Yingst D,Bloor R et al.Viscoacoustic waveform inversion of velocity structures in the time domain.Geophysics,2014,79(3):R103-R119.
[19] 李金丽,刘建勋,姜春香等.黏声VTI介质正演模拟与照明分析.石油地球物理勘探,2017,52(5):906-914. Li Jinli,Liu Jianxun,Jiang Chunxiang et al.Forward modeling and illumination analysis in visco-acoustic VTI media.OGP,2017,52(5):906-914.
[20] Bohlen T.Parallel 3-D viscoelastic finite difference seismic modeling.Computers & Geosciences,2002,28(8):887-899.
[21] 白璐,韩立国,张盼等.最小平方滤波法时间域全波形反演.石油地球物理勘探,2016,51(4):721-729. Bai Lu,Han Liguo,Zhang Pan et al.Time-domain full waveform inversion based on least square filter.OGP,2016,51(4):721-729.
[22] Tarantola A.Inverse Problem Theory and Methods for Model Parameter Estimation.Society for Industrial and Applied Mathematics,2005.
[23] 张广智,孙昌路,潘新朋等.快速共轭梯度法频率域声波全波形反演.石油地球物理勘探,2016,51(4):730-737. Zhang Guangzhi,Sun Changlu,Pan Xinpeng et al.Acoustic full waveform inversion in the frequency domain based on fast conjugate gradient method.OGP,2016,51(4):730-737.
[24] Kamei R and Pratt R G.Inversion strategies for visco-acoustic waveform inversion.Geophysical Journal International,2013,194(2):859-884.
[25] Choi Y and Alkhalifah T.Source-independent time-domain waveform inversion using convolved wavefields: Application to the encoded multisource waveform inversion.Geophysics,2011,76(5):R125-R134.
[26] Asnaashari A,Brossier R,Garambois S et al.Regula-rized seismic full waveform inversion with prior model information.Geophysics,2013,78(2):R25-R36.
