起伏地表地震波旅行时混合网格线性插值射线追踪计算方法
2018-03-10李庆春
王 琦 朱 盼 叶 佩 李 勤 李庆春*
(①长安大学地质工程与测绘学院,陕西西安 710054; ②中国国土资源航空物探遥感中心,北京 100083; ③西安科技大学地质与环境学院,陕西西安 710054)
1 引言
旅行时线性插值(Linear traveltime interpolation 简称LTI)是Asakawa等[1]提出的基于线性假设网格单元扩展射线追踪算法。由于该方法计算速度快、原理简单,得到了很大发展。赵改善等[2]结合界面二次源法将该方法推广于追踪反射波旅行时;聂建新等[3]将旅行时二次插值与线性插值方法联合,降低了累积误差;张赛民等[4]用抛物线插值取代线性插值,改善了因线性引起的误差;张东等[5]为了求得最小走时,在向前处理过程中采用了多方向循环的计算方法。
近年来多次波越来越引起人们关注,对多次波的正确模拟和认识是压制多次波干扰的前提。目前对多次波的射线追踪以基于网格单元扩展的方法为主。Rawlinson等[6]利用快速步进法结合分区多步计算技术实现了层状介质中多次透射波和多次反射波的计算,De Kool等[7]将此方法扩展到三维球面坐标系中;唐小平等[8]实现了分区多步改进的最短路径算法,可在二维和三维层状介质中追踪透射、反射(或折射)和转换的多次波;赵瑞等[9]提出了分区多步不规则最短路径算法,也可实现多次波的追踪计算,并与分区多步FMM算法进行对比,认为此方法比分区多步FMM算法具有高精度和高效率的优势。本文为了说明分区多步LTI算法的优势,与文献[9]中的分区多步FMM算法和分区多步ISPM算法的计算精度和效率亦做了比对。
关于起伏地表地震波传播问题,近年来国内外学者开展了相关研究。岳玉波等[10]用插值函数对起伏界面进行拟合,利用两点射线追踪方法实现了均匀速度模型中初值射线路径计算,但这种方法计算效率较低; 孙章庆等[11]在矩形网格中针对起伏地表改进了快速步进法(FMM),实现了起伏地表条件下的旅行时计算,此方法的网格仍然是单一的矩形网格,计算过程中如果网格过于稀疏会使界面呈阶梯状,引起较大误差,加密网格又会使计算效率大打折扣且仍不能很好地逼近起伏地表或复杂构造形态; 孙章庆等[12]用FMM法中窄带技术代替传统的LTI法的波前扩展方式实现了起伏地表射线追踪,该方法采用三角网与矩形网相结合的方式对模型进行剖分,使起伏地表下地震波走时的计算精度得到了提高,但并未涉及到多次波和转换波走时的计算; Lelièvre 等[13]利用基于不规则网格的FMM法计算三维起伏地表模型的初至波旅行时,但该方法无论是在网格剖分还是在旅行时计算阶段,计算量都非常大,而且此基于不规则网格的方法仅可以处理剖分三角形为锐角的情况。Sun等[14]提出在起伏地表附近采用间距不均一的网格剖分模型,用FMM法实现了起伏地表走时计算,但该方法需要对起伏地表的走时进行插值处理,这样势必会引起误差; Lan等[15]通过求解曲线坐标系下的程函方程,实现了起伏地表下各向异性介质的射线追踪,该方法为精确求解,需要对求解区域进行精细剖分,会严重影响计算效率; 赵后越等[16]利用规则网格和非规则网格相结合的方式进行网格剖分,结合最短路径法实现了各向异性起伏地表条件下初至波射线追踪,此方法为了提高计算精度会在网格边界加入新的节点,但同时降低了运算效率。此外国内外许多学者也对基于网格单元扩展的射线追踪算法做了有益的研究[17-26]。本文从网格剖分方式和局部走时计算两个方面出发开展研究,提出一种能更好地逼近真实界面和更加精确高效地计算起伏地表下地震波旅行时的方法,文中讨论了该方法的稳定性,用理论模型试算说明该方法具有良好的适应性。
2 矩形网格LTI方法的基本原理

图1 矩形网格局部旅行时计算示意图 (a)射线从矩形网格的横边穿过; (b)射线从矩形网格的纵边穿过
(1)
其中tb≥ta。根据几何关系,C点的旅行时可以表示为
(2)
(3)
可解出
(4)
进而可以求得D点的坐标
(5)
则C点的旅行时可表示为

(6)
在矩形网格中所有边界不是垂直就是水平的,当点A、B位于横边时,za=zb,如图1a所示,对应的公式可简化为
(7)
(8)
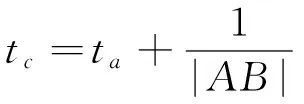
(9)
当点A、B位于纵边时xa=xb,如图1b所示,对应的公式可简化为
(10)
(11)
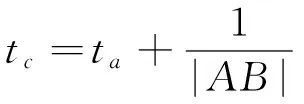
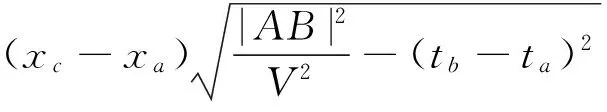
(12)
仅考虑以上两种情况,即可得到矩形网格LTI方法关于D点的坐标与tc的计算公式。
LTI算法的实现过程可分为向前和向后两个步骤进行。
第一步(向前处理):从炮点开始,据式(6)计算炮点到网格边界上各个节点的最小旅行时;
第二步(向后处理):从检波点开始,按式(5)计算所有射线路径与各个网格边界的交点。
以上每一步的实现过程均在文献[1]中有详细叙述,这里不再赘述。
3 混合网格LTI射线追踪方法
混合网格LTI方法的实现过程可以分为三个步骤:①模型剖分:②计算局部旅行时;③计算目标类型地震波旅行时。
3.1 模型剖分
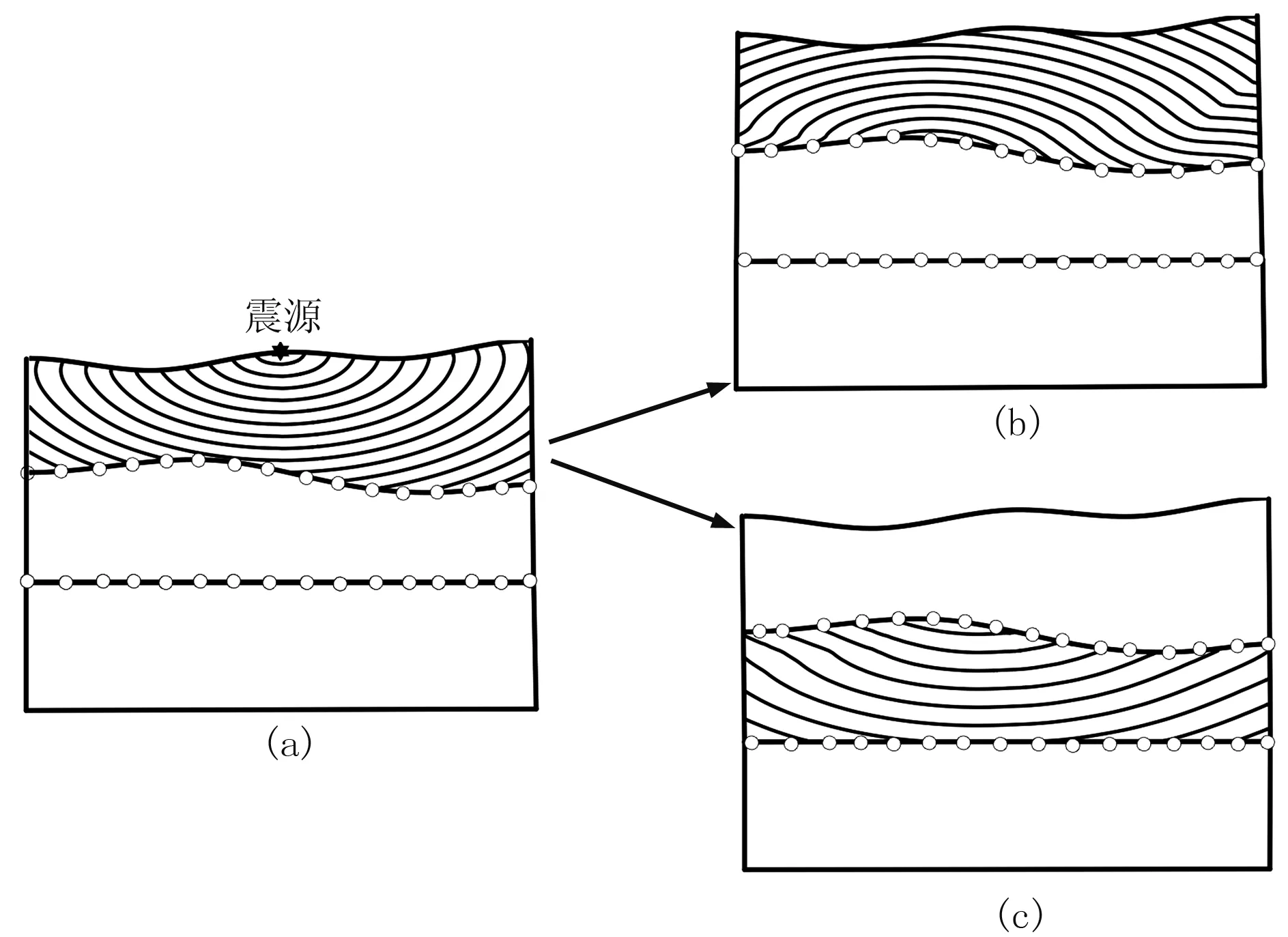
为了更接近实际地表或速度界面,同时又能兼顾计算效率,本文采用矩形网格与不规则四边形网格相结合的方法对模型进行剖分,如图2所示。首先对整个模型区域用矩形网格剖分,对地表和速度界面函数分别计算与网格纵边的交点,得到离散点地表点和速度界面点; 然后将相邻的界面离散点或网格节点选择性连接,构成一条由多条折线段组成近似于实际地表或速度界面的折线,把这些折线段与原矩形网格边界和节点组合,就构成了不规则四边形网格; 最后对除地表以上的各个网格节点赋予相应速度值,就完成了对整个模型的剖分。
上述混合网格在对模型剖分时会遇到三种情况:①地表或速度界面3个相邻的离散点都在原矩形网格的同一层内;②地表或速度界面3个相邻离散点中左端或右端的离散点与其余两个不在原矩形网格的同一层内;③地表或速度界面3个相邻离散点中两端的离散点与中间的离散点不在原矩形网格的同一层内。以上所述的三种情况分别对应于图2中编号为①、②、③的阴影部分,为了便于观察,将阴影部分按顺序放大,如图3所示。情况①时直接连接三个相邻的离散点即可构成不规则四边形网格(图3中的①);情况②时首先连接在原矩形网格同一层的两个离散点,然后连接地表或界面与纵边界无交点的原矩形网格的左下(或右下或左上或右上)角节点与中间离散点,构成非规则四边形网格(图3中的②);情况③时分别连接地表或界面与纵边界无交点的原矩形网格的左下(或右下或左上或右上)角节点、右下(或左下或左上或右上)角节点与中间离散点,构成不规则四边形网格(图3中的③)。图3中各个颜色不同的区域组成了利用上述方法建立的混合网格。
图2和图3中蓝色实线代表单一矩形网格剖分时对地表或界面的逼近,红色实线代表在混合网格剖分时逼近的地表或界面。可以看出后者对地表或界面的拟合程度更高,剖分方法也更加合理。
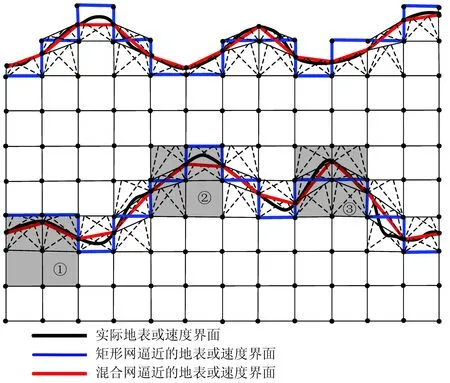
图2 混合网中模型剖分与局部旅行时计算示意图
3.2 混合网格LTI局部旅行时计算公式的建立
通过前两节的分析得知,适用于矩形网格的局部旅行时计算公式并不适用于混合网格,因此首先要建立针对不规则四边形的局部旅行时计算公式。
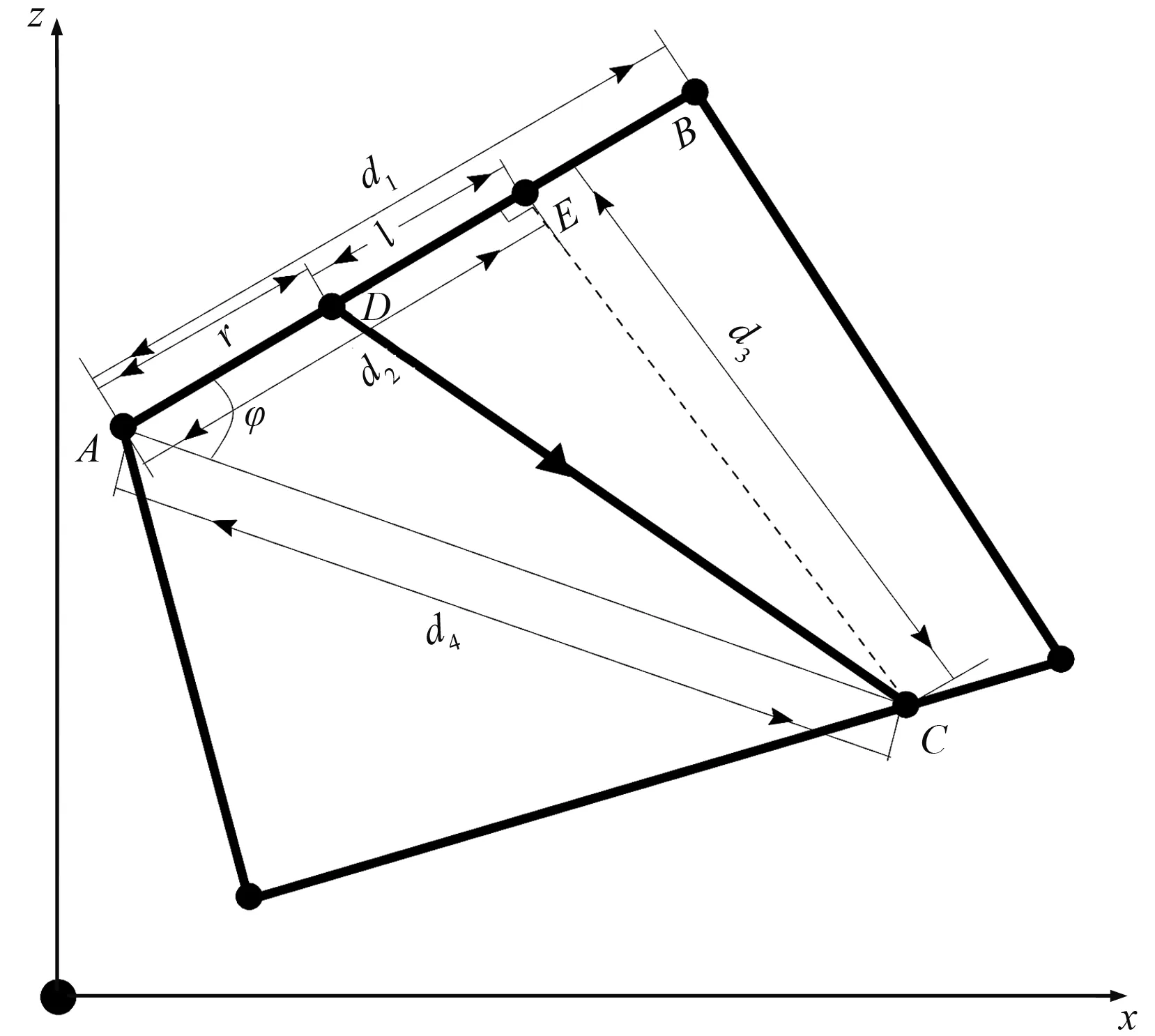
图4 不规则四边形网格中局部旅行时计算示意图
设A、B点所在直线的方程为Ax+Bz+C=0,分别将A、B点的坐标代入即可得
(za-zb)x-(xa-xb)z+za(xa-xb)-
xa(za-zb)=0
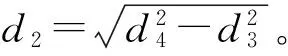
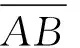
(13)
上式中tb>ta, Δt=tb-ta,求得td后,由几何关系,C点的旅行时可以表示为
(14)
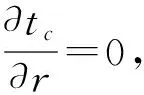
(15)

(16)
(17)
将式(16)、式(17)代入式(15)得
(18)
再将式(16)、式(17)、式(18)代入式(14)便得到了适用于不规则四边形网格局部走时的计算公式
(19)
D点的坐标可由A、B点的坐标线性插值得到
(20)
以上即为不规则四边形网格下求解tc和(xd,zd)的基本公式。
3.3 稳定性分析
在3.2的推导过程中,从tc关于r的一阶偏导数为零,即
(21)
可以得出: Δt的符号必须与d2-r的符号一致,否则在实数域内无极值点存在。此外,D点必须介于A、B点之间或与B点(A点)重合,否则计算得到的结果无实际物理意义,或与前提假设不符。记点D与点E之间的距离为l,则
(22)
理论上l的取值存在7种情况:
(1)xd∈(xa,xe),且zd∈(za,ze),则l∈(0,d2);
(2)xd∈(xe,xb),且zd∈(ze,zb),则l∈(-d1+d2,0);
(3)xd=xe,且zd=ze,则l=0;
(4)xd=xa,且zd=za,则l=d2;
(5)xd=xb,且zd=zb,则l=-(d1-d2);
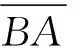
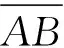
(23)
或
(24) (25) 当l∈(-∞,-d1+d2)时,求得 有 (26) 故后两种情况无实际物理意义,在这里不予考虑。在式(19)、式(20)的基础上针对以上前5种情况单独考虑,可得到每种情况的表达式 (27) (28) (3)xd=xe,且zd=ze时,r=d2,此时Δt=0,代入式(19)、式(20),得 tc=ta+sd3或tc=tb+sd3 (29) (30) (31) (32) (33) (34) 以上叙述建立了不规则四边形网格局部旅行时的计算公式,并且对其稳定性做了分析。针对每种情况分别利用相应的公式就可以稳定且高效地计算出tc和(xd,zd)。 本文提出的方法与分区多步计算技术[6]结合,就可以追踪任意多次反射(或反射转换)或透射(或透射转换)波。旅行时的计算分为向前处理和向后处理两个过程,在向前处理过程中计算每个网格节点的最小旅行时,向后处理过程是对射线路径的追踪以及计算整条射线路径旅行时之和。在计算反射波或透射波的旅行时时需要引入分区多步的思想,即将整个模型区域按所需追踪的波的类型和速度特征分成几个独立的计算区域,然后按照所分计算区域,在每个区域内独立进行计算。要运用分区多步计算技术,首先要建立模型并网格化(这里采用混合网格进行剖分),速度界面也要离散成不连续的点。 3.4.1 模型分区 图5a所示为多次反射波在二维层状介质模型中的分区情况,图中展示了一条在界面折返三次的多次反射波。根据分区多步的思想,该多次反射波旅行时的计算过程可以在四个独立的计算区域(图中1、2、3、4代表4个分区)内进行。具体实现过程如下。该多次反射波由四段组成: 第一段是来自地表到第二个反射界面的的下行波,在计算时将第一、二层作为第一个分区来计算第一段下行波的波前; 第二段是自第二个反射界面上的反射点到第一个反射界面的上行波,在计算时将第二层作为第二个分区来计算第二段上行波的波前;第三段是自第一个反射界面反射点到第二个反射界面的下行波,在计算时将第二层作为第三个分区来计算第三段下行波的波前;第四段是自第二个反射界面反射点到地表的上行波,在计算时将第一、二层作为第四个分区来计算第四段上行波的波前。 图5b所示为多次透射转换波在二维层状介质模型中的分区情况,图中展示了一条在界面两次透射、一次反射、三次转换(射线每透过一次界面或每反射一次就发生一次转换)的转换波射线。按照分区多步思想,该多次透射转换波旅行时的计算过程可以在四个独立的计算区域(图中1、2、3、4代表4个分区)内进行。假设该射线初始入射为P波,则第一段是自地面到第一个透射界面的下行P波,在计算时将第一层作为第一个分区来计算第一段下行P波的波前,此时计算所用速度为第一层的P波速度;第二段是自第一层透射点到第二层反射界面的下行S波,在计算时将第二层作为第二个分区来计算第二段下行S波的波前,此时计算所用速度为第二层的S波速度;第三段是自第二层反射点到第一层透射界面的上行P波,在计算时将第二层作为第三个分区来计算第三段上行P波的波前,此时计算所用速度为第二层的P波速度;第四段是自第一层透射点到地表的上行S波,在计算时将第一层作为第四个分区来计算第四段上行S波的波前,此时计算所用速度为第一层的S波速度。这样就可以追踪P-P波、P-S波、S-S波、S-P波。 图5 二维层状介质模型中多次反射、透射转换波分区示意图 (a)多次反射波; (b)多次透射转换波 3.4.2 多步计算 图6所示为反射(或反射转换)或透射(或透射转换)波的波前扩展示意图,具体实现过程如下。 图6 波前分区扩展示意图 (a)波前由震源扩展到速度界面离散点; (b)若反射,由界面离散点旅行时计算上行波波前; (c)若透射,由界面离散点旅行时计算下行波波前 (1)计算由震源到第一个分区下界面的下行波的波前,并找出界面离散点上走时最小的点,如果是P波入射,则计算时用P波速度,如果是S波入射,则计算时用S波速度,如图6a所示。 (2)将步骤(1)中计算出的走时最小的界面离散点作为新的震源。如果需要计算反射波的波前:由界面上新的震源向上计算上行波在该分区内的波前,如图6b所示,如果需要追踪转换波,则采用转换波的速度即可计算其相应的波前。如果需要计算透射波的波前:由界面上新的震源向下计算下行波在该分区内的波前,如图6c所示,如果需要追踪转换波,则采用转换波的速度即可计算其相应的波前。 (3)结合步骤(1)、步骤(2)计算波前,可以追踪任意多次反射(或反射转换)或透射(或透射转换)波。 (4)由以上三个步骤计算波前,再结合LTI的向后处理就可以追踪各类型波的射线路径。 为了验证本文提出的计算方法的计算精度和效率,首先将分区多步LTI算法分别与分区多步FMM算法和分区多步ISPM算法的计算精度及效率进行比对,再选取三个速度模型,分别为起伏地表一维线性增加速度模型、带有垂直断层的层状介质模型和加上起伏地表与速度界面的的等价Marmousi模型,进行试算。对第一个模型分别用分区多步矩形网格和混合网格LTI法计算多次反射波的旅行时,对比分析算法的计算精度。对第二个模型分别追踪层间多次反射波和多次透射转换波,对第三个模型追踪其层间多次反射波,合成各个目标波形的地震记录。 目前基于网格单元波前扩展的多次波波前追踪方法中较为成熟的主要有分区多步FMM算法和分区多步ISPM算法。为了验证分区多步LTI算法的计算精度和计算效率,对同一个速度模型分别用以上三种方法,在4种网格间距下计算反射波走时。模型尺寸为100km×40km,速度为4000m/s,地表水平,在30km处有一条水平反射界面。在模型参数化时,分区多步FMM算法中正方形网格尺寸分为四种尺度,分别为1000m×1000m、500m×500m、250m×250m和125m×125m;分区多步ISPM算法中网格尺寸为4000m×4000m,并在网格单元边界上相应加入3、7、15和31个次级节点;分区多步LTI算法中网格大小和分区多步FMM算法中设置相同,这样保证了以上三种方法中网格节点的间距相同。炮点在模型的左上角坐标为(0,0),100个检波器等间距(1000m)排列在地面,最小炮检距为1000m。图7和图8分别给出了随炮检距变化的分区多步FMM算法(图7a),分区多步ISPM算法(图7b)和分区多步LTI算法(图8)相对于解析解在4种不同节点距下反射波走时的相对误差。表1给出了三种方法分别所用CPU耗时。从图7、图8和表1中可见,除了网格间距为1000m×1000m的情形外分区多步LTI算法的精度均优于分区多步FMM和分区多步ISPM算法,在计算效率方面,分区多步LTI算法明显优于分区多步FMM算法而低于分区多步ISPM算法。 图7 随着炮检距变化的FMM算法 图8 随着炮检距变化的分区多步LTI算法数值解相对于解析解在4种不同网格距下反射波旅行时的相对误差 表1 均匀速度模型中FMM、ISPM和分区多步LTI算法 在4种不同网格间距下CPU耗时对比表 注:表中FMM和ISPM算法数据引自文献[9] 图9a是一个大小为400m×400m、每一层的速度皆为一维线性增加的三层速度模型,其速度表达式如图9a中所列,其中h1、h2、h3表示每一层的厚度。炮点置于(200m,-20m)处,在地表上布设101个检波点,横向道间距均为4m,模型中剖分网格尺寸(在混合网格中仅指横向网格间距)分别为0.1m×0.1m、0.2m×0.2m、0.4m×0.4m、1.0m×1.0m、2.0m×2.0m和4.0m×4.0m, 分别利用本文提出的方法和完全矩形网剖分的方法计算自炮点经界面三次折返到起伏地表检波点的射线路径的旅行时。 Kim[27]通过改变节点间距的方法来做误差分析,此方法的前提是误差收敛。认为随着网格间距的缩小,误差也会随之减小,最终收敛于最小值;反之,随着网格间距增大,误差也会随之向上浮动。 本文采用此方法进行误差分析。为了验证本文所采用的方法比矩形网LTI法在进行多次反射波射线追踪时的数值稳定性以及射线路径的可靠性更好,本文通过改变网格单元大小进行误差分析,以最小网格单元尺寸为0.1m×0.1m的结果作为参考值,计算出其他五种网格单元尺寸相对于单元尺寸为0.1m×0.1m时各检波点的多次反射波旅行时的相对误差。 从图9b(采用分区多步混合网LTI算法)、图9c(采用分区多步矩形网LTI算法)和表2中可以看出:两种算法计算多次反射波旅行时所得的误差都随网格大小缩小而逐渐收敛。但相比较而言,利用分区多步混合网格LTI算法所计算的旅行时的误差总体上要低于分区多步矩形网格LTI算法,除网格尺寸为4.0m×4.0m以外,其余网格尺寸下计算的相对误差基本在0.3%以内,且在相同网格尺寸下,分区多步混合网格LTI算法的计算精度高于分区多步矩形网格LTI算法,在保证精度相当的条件下,分区多步混合网格LTI算法的计算效率高于分区多步矩形网格LTI算法。据此说明分区多步混合网格LTI算法是稳定的,进行多次反射波模拟的射线路径是可靠的。 图10为在(200m,-20m)处单炮激发、11道接收的多次反射波波前在每个计算区域内的扩展过程和多次波的射线路径。从图10b~图10e波前在各个计算区域中的扩展过程和方式可以看出,在速度均匀的同一区域内波前大致呈相互平行的弧线。当波前穿过速度分界面时,就会随速度的改变发生变化,这是由速度分界面两边的速度变化引起的,这种现象符合地震波在层状介质中的传播规律。图10g为根据图10a模型模拟计算的单炮合成地震记录,在合成记录中分别显示了直达波、来自Ⅰ与Ⅱ波阻抗界面的一次反射P波以及多次反射P波。从图10g中可以看出, ②与②*相比完全不一致,如A、B两处相差较大,这是由于检波点分别位于水平地表和起伏地表引起的,即如果将反射波静校正到虚拟的水平地表(浮动基准面),地震记录就会出现上述问题,不能客观地反映界面的实际位置。 表2 图9a所示模型由分区多步混合网格LTI和分区多步矩形网LTI计算所得的 多次反射波旅行时的误差、相对误差和CPU在5种不同网格尺寸下对比表 图10 层间多次波波前在各分区中传播过程及射线路径(波前间隔为0.01s) (a)模型参数和分区编号; (b)下行P波波前在第一个分区内传播; (c)上行P波波前在第二个分区内传播; (d)下行P波波前在第三个分区内传播; (e)上行P波波前在第四个分区内传播; (f)层间多次波射线路径; (g)单炮合成记录 图11为在(200m,-20m)处单炮激发、11道接收的多次透射转换波波前在各个分区中的传播过程以及多次透射转换波的射线路径。从图11b~图11e中波前在各个分区中的传播过程可以看出,当波前以横波速度传播时,波前的等时线较密(如图11c、图11e),当波前以纵波速度传播时波前等时线相对较为稀疏(如图11b、图11d),这是因为横波传播速度相对于纵波传播速度较慢,符合地震波在介质中的传播规律。从图11f中可以看出:在各个速度均匀的分层中,射线路径是直线,但是通过速度分界面时射线就会发生偏折。若入射的是S波,透射或反射为P波时,相应的出射角或反射角会增大;若入射的是P波,透射或反射为S波,相应的出射角或反射角会减小,这符合斯奈尔定律。可以说明在计算时分区彻底,计算方法正确,方法灵活性较强,可以追踪到层状介质中各种透射、转换、反射波的射线路径和旅行时。图11g为在图11a中模拟的单炮合成记录。记录中分别显示了各道直达波、分别来自Ⅰ与Ⅱ波阻抗界面的P-P波、P-S波、图10f中所示的多次反射P波以及图11f中所示的多次透射转换波。 图12为在人为划定剧烈起伏地表和两条反射界面(图12a中加粗的黑色实线)后的Marmousi模型中,在(2500m,-500m)处单炮激发、11道接收的多次反射P波波前在各个分区中的传播及射线路径。由图12b~图12e中可以看出,波前在扩展过程中在速度较高的区域等时线被拉伸,在速度较低的区域等时线被压缩,且波前等时线连续,满足地震波的传播规律,说明基于混合网格剖分的LTI方法对构造复杂的速度模型有很强的适应能力,适用于复杂速度模型的多次波模拟。图12g给出了在图12a的模型中模拟的单炮合成记录。在合成记录中可以看到初至波、分别来自于第Ⅰ与第Ⅱ波阻抗界面的一次反射P波和图12f所示的多次反射P波。 图11 多次透射转换波波前在各分区中的传播过程及射线路径(波前间隔为0.01s) (a)模型参数和分区编号; (b)下行P波波前在第一个分区内传播; (c)下行S波波前在第二个分区内传播;(d)上行P波 波前在第三个分区内传播; (e)上行S波波前在第四个分区内传播; (f)多次透射转换波射线路径; (g)单炮合成记录 (a)模型参数和分区编号; (b)下行P波波前在第一个分区内传播; (c)上行P波波前在第二个分区内传播; (d)下行P波波前在第三个分区内传播; (e)上行P波波前在第四个分区内传播; (f)层间多次波射线路径; (g)带地形的Marmousi模型单炮合成记录 本文提出了用在矩形中加入不规则四边形网格后形成的混合网格来取代单一矩形网格对模型进行剖分,提高了对起伏地表和速度界面的处理能力,在矩形网格局部旅行时计算公式的基础上,建立了适用于混合网格局部旅行时计算的公式,并证明了该公式的稳定性。利用分区多步混合网格LTI法实现了相关类型地震波(初至波、一次反射波、多次反射波、多次透射转换波)旅行时的计算和射线路径的追踪。 通过对带地形的层状模型和速度不均匀模型的试算,不但说明了该方法的计算结果精度高于同等网格间距下的矩形网格LTI方法,而且证明了该方法对复杂速度模型具有良好的适应能力。为起伏地表和复杂构造情况下地震波旅行时的计算提供了一种新的方法。 [1] Asakawa E and Kawanaka T.Seismic ray tracing using linear traveltime interpolation.Geophysical Prospecting,1993,41(4):99-111. [2] 赵改善,郝守玲.基于旅行时线性插值的地震射线追踪算法.石油物探,1998,32(2):14-24. Zhao Gaishan,Hao Shouling.Seismic ray tracing algorithm based on the linear traveltime interpolation.GPP,1998,32(2):14-24. [3] 聂建新,杨慧珠.地震波旅行时二次/线性联合插值法.清华大学学报,2003,43(11):1495-1498. Nie Jianxin,Yang Huizhu.Quadrarical linear travel time interpolation of seismic ray-tracing.Journal of Tsinghua University,2003,43(11):1495-1498. [4] 张赛民,周竹生,陈灵君等.对旅行时进行抛物型插值的地震射线追踪方法.地球物理学进展,2007,22(1):43-48. Zhang Saimin,Zhou Zhusheng,Chen Lingjun et al.Seismic ray tracing method of applying parabolic interpolation to travel time.Progress in Geophysics,2007,22(1):43-48. [5] 张东,谢宝莲,杨艳等.一种改进的线性旅行时插值射线追踪算法.地球物理学报,2009,52(1):200-205. Zhang Dong,Xie Baolian,Yang Yan et al.A ray tra-cing method based on improved linear traveltime interpolation.Chinese Journal of Geophysics,2009,52(1):200-205. [6] Rawlinson N,Sambridge M.Multiple reflection and transmission phases in complex layered media using multistage fast marching method.Geophysics,2004,69(5):1338-1350. [7] De Kool M,Rawlinson N,Sambridge M.A practical grid based method for tracking multiple refraction and reflection phases in three-dimensional heterogeneous media.Geophysical Journal International,2006,167(1):253-270. [8] 唐小平,白超英.最短路径算法下三维层状介质中多次波追踪.地球物理学报,2009,52(10):2635-2643. Tang Xiaoping,Bai Chaoying.Multiple ray tracing within 3-d layered media with the shortest path me-thod.Chinese Journal of Geophysics,2009,52(10):2635-2643. [9] 赵瑞,白超英.复杂层状模型中多次波快速追踪——一种基于非规则网格的最短路径算法.地震学报,2010,32(4):433-444. Zhao Rui,Bai Chaoying.Fast multiple ray tracing within complex layered media: the shortest path method based on irregular grid cells.Acta Seismologica Sinica,2010,32(4):433-444. [10] 岳玉波.起伏地表下初值射线追踪的实现.勘探地球物理进展,2007,30(5):388-391. Yue Yubo.Realization of initial value ray tracing for rugged topography.Progress in Exploration Geophy-sics,2007,30(5):388-391. [11] 孙章庆,孙建国.波前快速推进法起伏地表地震波走时计算.勘探地球物理进展,2007,30(5):92-97. Sun Zhangqing,Sun Jianguo.Traveltime computation using fast marching method from rugged topography.Progress in Exploration Geophysics,2007,30(5):92-97. [12] 孙章庆,孙建国,韩复兴.复杂地表条件下基于线性插值和窄带技术的地震波走时计算.地球物理学报,2009,52(11):2846-2853. Sun Zhangqing,Sun Jianguo and Han Fuxing.Traveltimes computation using linear interpolation and narrow band technique under complex topographical conditions.Chinese Journal of Geophysics,2009,52(11):2846-2853. [13] Lelièvre P G,Farquharson C G and Hurich C A.Computing first-arrival seismic traveltimes on unstructured 3-D tetrahedral grids using the fast marching method.Geophysical Journal International,2011,184(2):885-896. [14] Sun Jianguo,Sun Zhangqing and Han Fuxing.A finite difference scheme for solving the eikonal equation including surface to topography.Geophysics,2011,76(4):53-56. [15] Lan Haiqing and Zhang Zhongjie.Topography-dependent eikonal equation and its solver for calculating first-arrival traveltimes with an irregular surface.Geophysical Journal International,2013,193(2):1010-1026. [16] 赵后越,张美根.起伏地表条件下各向异性地震波最短路径射线追踪.地球物理学报,2014,57(9):2910-2917. Zhao Houyue,Zhang Meigen.Tracing seismic shortest path rays in anisotropic medium with rolling surface.Chinese Journal of Geophysics,2014,57(9):2910-2917. [17] 孙章庆.起伏地表条件下的地震波走时与射线路径计算[学位论文].吉林长春:吉林大学,2011. Sun Zhangqing.The Seismic Traveltimes and Ray Path Computation under Undulating Earth’s Surface Condition[D].Jilin University,Changchun,Jilin,2011. [18] 李永博,李庆春,吴琼等.快速行进法射线追踪提高旅行时计算精度和效率的改进措施.石油地球物理勘探,2016,51(3):467-473. Li Yongbo,Li Qingchun,Wu Qiong et al.Improved fast marching method for higher calculation accuracy and efficiency of traveltime.OGP,2016,51(3):467-473. [19] 王珺,李永庆.遗传算法和正交时频原子相结合的地震记录快速匹配追踪.石油地球物理勘探,2016,51(5):881-888,893. Wang Jun,Li Yongqing.Seismic trace fast matching pursuit based on genetic algorithm and orthogonal time-frequency atom.OGP,2016,51(5):881-888,893. [20] 秦宁,王延光,杨晓东等.非水平地表高斯束叠前深度偏移及山前带应用实例.石油地球物理勘探,2017,52(1):81-86. Qi Ning,Wang Yanguang,Yang Xiaodong et al.Gaussian bean prestack depth migration for undula-ting-surface area in piedmont zone.OGP,2017,52(1):81-86. [21] 黄国娇,白超英.二维复杂层状介质中地震多波旅行时联合反演成像.地球物理学报,2010,53(12): 2972-2981. Huang Guojiao,Bai Chaoying.Simultaneous inversion with multiple traveltimes within 2-d complex layered media.Chinese Journal of Geophysics,2010,53(12):2972-2981. [22] 桑运云,孙晓军.起伏地表下基于抛物插值的最短路径射线追踪.石油物探,2014,53(2):1441-1448. Sang Yunyun,Sun Xiaojun.Shortest path raytracing based on parabolic traveltime interpolation in irregular topography.GPP,2014,53(2):1441-1448. [23] 侯爵,张忠杰,兰海强等.起伏地表下地震波传播数值模拟方法研究进展.地球物理学进展,2014,29(2):488-497. Hou Jue,Zhang Zhongjie,Lan Haiqiang et al.Progress in numerical simulation of seismic wave propagation under an undulating surface.Progress in Geophysics,2014,29(2):488-497. [24] 孙章庆,孙建国,韩复兴.基于线性插值和窄带技术的走时计算方法.石油地球物理勘探,2009,44(4):436-441. Sun Zhangqing,Sun Jianguo and Han Fuxing.Travel-time computation based on linear interpolation and narrow-band technique.OGP,2009,44(4):436-441. [25] 叶佩,李庆春.旅行时线性插值射线追踪提高计算精度和效率的改进方法.吉林大学学报(地球科学版),2013,43(1):291-298. Ye Pei,Li Qingchun.Improvements of linear traveltime interpolation ray tracing for the accuracy and efficiency.Journal of Jilin University (Earth Science Edition),2013,43(1):291-298. [26] 宋御杰.基于混合网格剖分的起伏地表旅行时计算方法研究[学位论文].陕西西安: 长安大学,2015. Song Yujie.The Travel-time Computation Method Study Under Undulating Earth’s Surface Based on Hybrid mesh[D].Chang’an University,Xi’an,Shaanxi,2015. [27] Kim S.3-D eikonal solvers: First-arrival traveltimes.Geophysics,2002,67(4):1225-1231.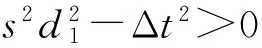
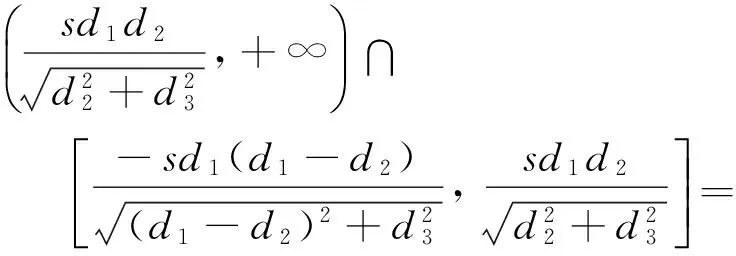
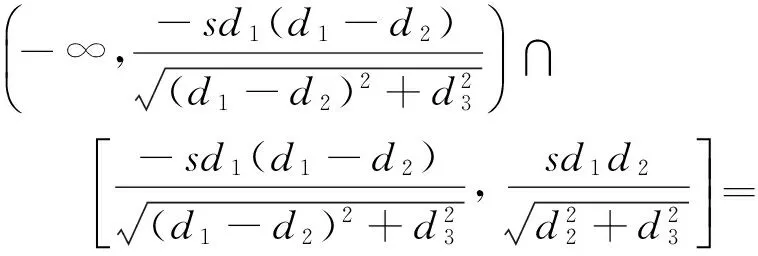
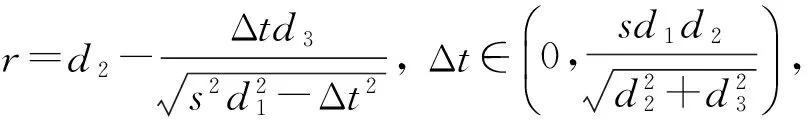
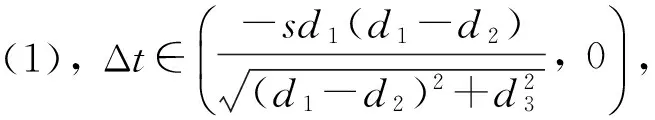
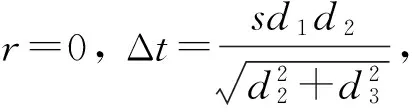
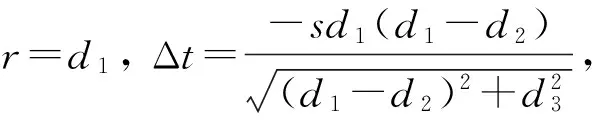
3.4 目标波型的旅行时计算

4 数值算例
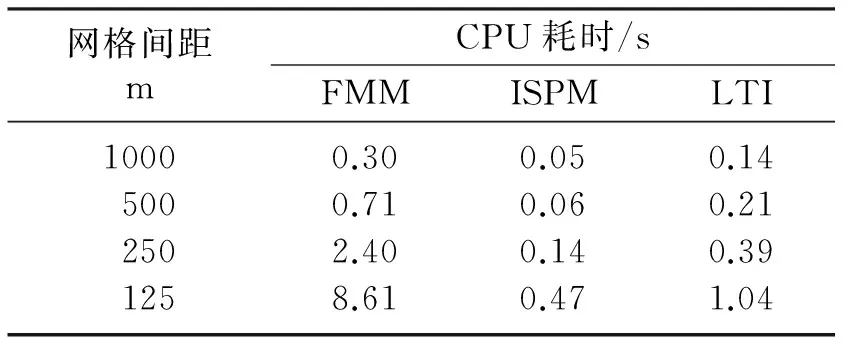
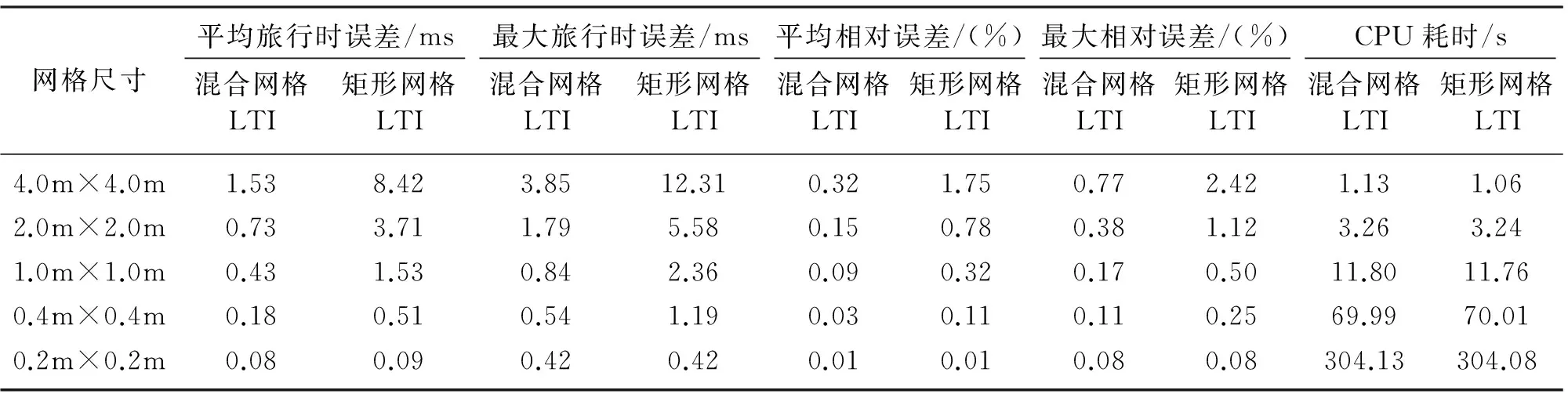
4.1 方法对比及精度分析

(a)和ISPM算法(b)数值解相对于解析解在4种不同网格距下反射波旅行时的相对误差(引自文献[9])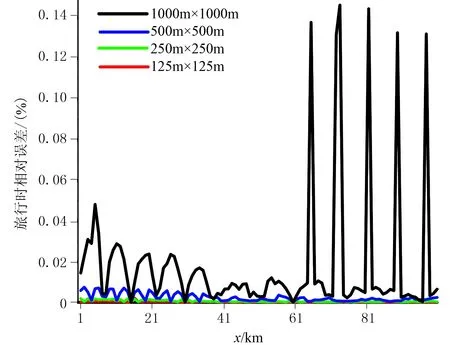
4.2 二维层状介质多次反射波模拟

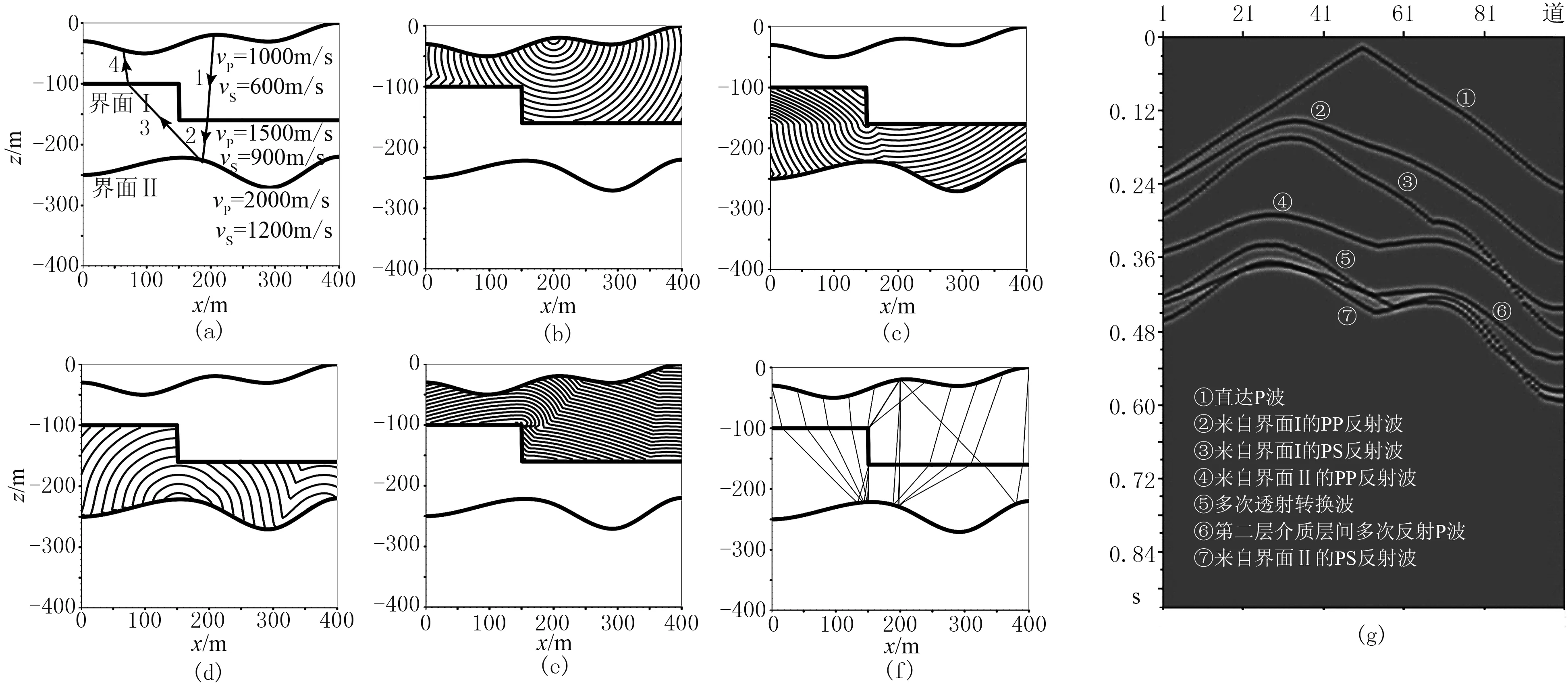
4.3 二维层状介质多次透射、转换、一次反射波模拟
4.4 Marmousi模型起伏检波点反射波及多次波模拟
5 结论
