Patient-Specific Echo-Based Fluid-Structure Interaction Modeling Study of Blood Flow in the Left Ventricle with Infarction and Hypertension

Longling Fan *, Jing Yao *, Chun Yang, Di Xu and Dalin Tang

1 Introduction

Intra-cardiac hemodynamics is closely related to ventricle cardiac functions. Therefore,analyzing ventricle blood flow characteristics may provide information and insight on heart disease development and treatment strategies. Peskin pioneered active heart modeling effort and simulated blood flow in a pumping heart with his immersed boundary method[Peskin (1977); McQueen and Peskin (2000)]. Chahboune et al. [Chahboune and Crolet(1998)] presented a contribution to the numerical simulation of the left ventricle (LV)taking into account simultaneously the fluid flow inside the cavity and the motion of the cardiac wall. Taylor et al. [Taylor, Okino andYamaguchi (1994)] investigated the effects of time-varying left ventricular ejection using computational fluid dynamics. Watanabe et al. [Watanabe, Sugiura, Kafuku et al. (2004)] incorporated the dynamics of the left atrium and pulmonary circulation into the model to simulate the ventricular filling dynamics. After that, various frameworks and methods have been proposed to simulate the flow pattern inside the LV during the filling phase [Lemmon and Yoganathan (2000); Vierendeels,Riemslagh, Dick et al. (2000); Baccani, Domenichini, Pedrizzetti et al. (2002); Cheng Oertel and Schenkel (2005); Arefin and Morsi (2014)]. Saber et al. [Saber, Gosman, Wood et al. (2001)] introduced the idea of three-dimensional magnetic resonance imaging (MRI)-based LV flow simulation. Long et al. [Long, Merrifield, Xu et al. (2008)] presented patient-specific modelling with MRI to investigate LV blood flow patterns in normal subjects. Our group introduced patient-specific cardiac magnetic resonance (CMR)-based right ventricle/left ventricle (RV/LV) fluid-structure-interaction (FSI) models with various surgical design and potential applications [Tang, Yang, Geva et al. (2007, 2008, 2010a,2010b, 2011)].

For studies linked to clinical applications, Delemarre et al. [Delemarre, Visser, Bot et al.(1990)] investigated the predictive value of the LV spatial flow pattern in order to identify patients who would develop a thrombus. Doenst et al. [Doenst, Spiegel, Reike t al. (2009)]developed a volume-independent quantitative technique to assess ventricular flow dynamics based on fluid dynamics modeling and tested the applicability of this method to patients with ischemic remodeling and surgical ventricular reconstruction (SVR).Khalafvand et al. [Khalafvand, Zhong and Ng (2014)] simulated the LV blood flow in patients with heart failure before and after SVR and normal subjects. They revealed that ventricular surgical restoration could improve ventricular function by modifying intraventricular blood flow. Zuo et al. [Zuo, Tang, Yang et al. (2015)] constructed right ventricle/left ventricle /patch models with FSI based on data from a canine patch model to identify mechanical conditions for myocardium tissue regeneration. Tang et al. [Tang, Zuo,Yang et al. (2017)] used computational RV/LV models to compare patients with tetralogy of Fallot (TOF) and healthy volunteers and found that TOF patients whose morphological and mechanical characteristics were close to healthy tend to have better cardiac outcome post to pulmonary valve replacement surgical procedures. Those modeling and simulations are of clear importance in clinical applications.

Myocardial infarction (MI) is a common complication of cardiac ischemia. However, the impact of MI on the LV flow patterns has not been fully investigated. Domenichini et al.[Domenichini and Pedrizzetti (2011)] studied the effect of an anterior-inferior MI on intraventricular vortical structures in a generic idealized LV geometry. Khalafvand et al.[Khalafvand, Ng, Zhong et al. (2012)] modeled patient specific LV flow in normal and abnormal heart from different patients including infarction. Chan et al. [Chan, Lim, Chee et al. (2013)] provided a comprehensive overview of computational fluid dynamics approaches to simulate blood flow in dilated cardiomyopathy (DCM) and MI during filling phase. Mangual et al. [Mangual, Kraigher-Krainer, De Luca et al. (2013)] studied on the changes in LV flow patterns in patients with DCM compared to healthy subjects.Imanparast et al. [Imanparast, Fatouraee and Sharif (2017)] presented an insightful numerical method that creates an artificial MI on an image-based fluid-structure interactional model of normal LV to investigate its influence on the flow in comparison with the normal case. Computational modeling based on patient-specific in vivo data comparing flow features of MI patients with healthy volunteers is lacking in the current literature.

In our previous study, Echo-based 3D LV models were introduced to quantify ventricle material properties and investigate morphological and mechanical stress/strain difference between ventricle with and without infarct [Fan, Yao, Yang et al. (2014); Fan, Yao, Yang et al. (2015, 2016)]. In this paper, LV FSI models base on patient-specific Echo imaging data for patients with hypertension, myocardium infarction (MI), and a healthy volunteer were constructed to investigate the impact of infarct and hypertension on flow behaviors including flow velocity, vorticity and flow shear stress (FSS). Results from those models were extracted for comparisons.

2 Data acquisition, models and methods

2.1 3D Echo data acquisition

Three patients were recruited to participate in this study with written consent obtained at the First Affiliated Hospital of Nanjing Medical University, Nanjing, China. Details of the data acquisition procedures were previously described [Fan, Yao, Yang et al. (2015)].Patient One (P1) is a healthy volunteer, male, 55 years old. Patient Two (P2) is a hypertension patient, male, 65 years old, no infarction. Patient Three (P3) had an inferior and posterior myocardial infarction before Echo image acquisition, male, 73 years old.Basic patient information is given in Tab. 1. Fig. 1 gives the end-systole Echo images and LV blood pressure profile for P3 and re-constructed 3D pressurized begin-filling and begin-ejection geometries for the three patients.

Table 1: Patient data and ventricle volume data

Figure 1: End-systole Echo images and LV blood pressure profile for P3 and reconstructed 3D pressurized begin-filling (BF) and begin-ejection (BE) geometries of all the three patients

2.2 The fluid-structure interaction model of LV

Blood flow in the left ventricle was assumed to be laminar, Newtonian, viscous and incompressible. The Navier-Stokes equations with arbitrary Lagrangian-Eulerian (ALE)formulation were used as the governing equations. To simplify the computational model,the cardiac cycle was split into two phases: (a) the filling phase (diastole) when the inlet was open, inlet blood pressure was prescribed (Fig. 1(b)), blood flows into the LV, and the outlet was closed (by setting flow velocity to zero); (b) The ejection phase (systole) when inlet was closed, outlet was open, outlet pressure was prescribed, and blood was ejected out of the LV. Pressure conditions were prescribed at the mitral (inlet) and aortic (outlet)valves . When the inlet or outlet was closed, flow velocity was set to zero and pressure was left unspecified. When the inlet or outlet was open, flow velocity was left unspecified and pressure was prescribed. No-slip boundary conditions and natural force boundary conditions were specified at all interfaces to couple fluid and structure models together[McCulloch, Waldman, Rogers et al. (1992); Bathe (1996); Bathe and Zhang (2004); Bathe and Ledezma (2007); Tang, Yang, Geva et al. (2010a, 2010b)]. The fluid model is given below:

where u and p are flow velocity and pressure, ugis mesh velocity, μ is the viscosity of blood. Γ stands for LV inner wall, f·,jstands for derivative of f with respect to the jth variable (or time t), σrand σsare fluid and structure stress tensors, and nrand nsare their outward normal directions, respectively.

The ventricle material/infarct tissue was assumed to be hyperelastic, anisotropic/isotropic,nearly-incompressible and homogeneous. The governing equations for the LV structure model were:

The nonlinear Mooney-Rivlin model was used to describe LV normal tissue (anisotropic)and infarct (isotropic) material properties. The strain energy function for the isotropic modified Mooney-Rivlin model is given by Tang et al. [Tang, Yang, Geva et al. (2010,2011)]:

where I1and I2are the first and second strain invariants given by,

C=[Cij]=XTX is the right Cauchy-Green deformation tensor, X=[Xij]=[∂xi/∂aj], (xi) is current position, (ai) is original position, ciand Diare material parameters chosen to match experimental measurements [Humphrey (2002); McCulloch (2007); Sacks and Chuong(1993); Tang, Yang, Geva et al. (2011)]. The strain energy function for the anisotropic modified Mooney-Rivlin model anisotropic model was obtained by adding an additional anisotropic term in Eq. (3) [Bathe (2002); Holzapfel, Gasser and Ogden (2000); Tang,Yang, Geva et al. (2010)]:

where I4=Cij(nf)i(nf)j, Cijis the Cauchy-Green deformation tensor, nfis the fiber direction,K1and K2are material constants [Bathe (2002)]. With parameters properly chosen, it was shown that stress-strain curves derived from Eq. (12) agreed very well with the stress-strain curves from the anisotropic (transversely isotropic) strain-energy function with respect to the local fiber direction given in [McCulloch, Waldman, Rogers et al. (1992, 2007)]:

where Effis fiber strain, Eccis cross-fiber in-plane strain, Erris radial strain, and Ecr, Efrand Efcare the shear components in their respective coordinate planes, C, b1, b2, and b3are parameters to be chosen to fit Echo LV volume variation data. For simplicity, b1, b2, and b3in Eq. (14) were kept as constants, C in Eq. (13) were chosen to fit Echo-measured LV volume data. Tab. 2 gave the LV material parameter values from the three patients. The effective Young’s modulus (YM) values of the anisotropic Mooney-Rivlin models over strain interval [1.0, 1.3] were used for each comparison. YM values in both fiber (YMf)and circumferential (YMc) directions were provided.

Table 2: Material parameter values comparison of three patients. YMf: YM in fiber direction, YMc: YM in circumferential direction

As patient-specific fiber orientation data was not available from these patients, we chose to construct a two-layer LV model and set fiber orientation angles using fiber angles given in Axel (2002) [Axel (2002)], Hunter et al. [Hunter, Pullan and Smaill (2003)]. Fiber orientation angles were set at -60 degree and 80 degree for epicardium (outer layer) and endocardium (inner layer), respectively. Fiber orientation can be adjusted when patientspecific data becomes available [Tang, Yang, Geva et al. (2008)].

2.3 A pre-shrink process and geometry-fitting technique for mesh generation

Under in vivo condition, ventricles are pressurized and the zero-stress ventricular geometries are not known. In our model construction process, a pre-shrink process was applied to in vivo end-systolic ventricular geometries to generate the starting shape (zeroload geometry) for the computational simulation. Initial shrinkage was needed so that when pressure was applied, the ventricle would regain its in vivo morphology. We started with an initial guess of shrinkage rate and material parameter values, constructed the model, and applied the LV minimum pressure (begin-filling pressure) to see if the pressurized LV volume would match in vivo LV volume data. If not, we would adjust the material parameter values, pressurize the ventricle and check again. The process was repeated until LV volume matched in vivo volume with error ＜0.01 cm3. The short-axis shrinkage was larger because the ventricle expanded mostly in the short-axis direction.

A geometry-fitting mesh generation technique developed in our previous studies was also used to generate mesh for our models [Yang, Tang, Yuan et al. (2008); Tang, Yang, Geva et al. (2008)]. Mesh analysis was performed by decreasing mesh size by 10% (in each dimension) until solution differences were less than 2%. The mesh was then chosen for our simulations.

2.4 Solution methods and data collection for statistical analysis

The Echo-based anisotropic LV models were constructed for the three patients and the models were solved by ADINA (ADINA R&D, Watertown, MA, USA) using unstructured finite elements and the Newton-Raphson iteration method. The “Re-Start” feature in ADINA was used to adjust material parameters at each numerical time step to implement the active contracting material properties. In this modeling approach, active contraction was achieved by material stiffening. With validation from actual LV volume measurements,our simulated LV motion and volume change can provide ventricular cardiac function assessment and flow and stress predictions for detailed mechanical analysis.

Because stress and strain are tensors, for simplicity, maximum principal stress (Stress-P1)and strain (Strain-P1) were used for analyses and model comparisons. They were referred to as stress and strain in this paper. For each LV data set (11 slices. Slices are short-axis cross sections), we divided each slice into 4 quarters, each quarter with equal inner wall circumferential length. Ventricle stress and strain were calculated at all nodal points (100 points/slice, 25 points/quarter). The “quarter” values of those parameters were obtained by taking averages of those quantities over the 25 points for each quarter and saved for analysis. For flow characteristics, flow velocity, vorticity (curl of velocity) and maximum shear stress were obtained for comparisons. Student t-test was used to compare the data from the three patients.

3 Results

Flow velocity and vortex patterns, flow shear stress, and ventricle structural stress and strain from the three patients were compared. Data from the healthy volunteer (P1) were used as baseline. Impact of infarct and hypertension was demonstrated by comparing data from MI (P3) and hypertension (P2) patients with data from the healthy volunteer.Dynamic 3D solutions have complex behaviors. It is common to use selected cut-surfaces and critical time points (begin-filling, peak velocity during filling, begin-ejection, peak velocity during ejection, etc.) to demonstrate and compare solution behaviors.

3.1 LV with MI had lower peak flow velocity and hypertension LV had higher peak flow velocity

Fig. 2 gave flow velocity plots on a selected cut surface at six time points in a cardiac cycle.Fig. 2(a-c) used one uniform scale and showed velocity magnitude at three time points in filling phase, while Fig. 2(d-f) used another uniform scale and showed velocity distributions at different time points in ejection phase. For our modeling set-up, the time points for begin-filling and end-ejection are connection points of systole and diastole phases. The same is true end-filling and before-ejection time points. This explanation should be helpful to understand why we mainly used begin-filling and begin-ejection in our comparative analyses.

During the filling phase, blood enters the left ventricle through the mitral valve, the aortic valve is closed, and the left ventricle expands. Fig. 2(a) showed the velocity distribution at begin of filling. As the pressure at the mitral valve increased, magnitude of velocity changed with the pressure gradient at the inlet. Fig. 2(b) and (c) showed the velocity distributions at two time points during filling phase. Moreover, Fig. 2(b) gave the peak of velocity magnitude during filling phase. Fig. 2(c) indicated that vortex were formed.During the ejection phase, aortic valve was open and mitral valve was closed. Blood was ejected out of the left ventricle through aortic valve due to LV elastic contraction. Fig. 2(d)showed the velocity distribution at begin of ejection. As the pressure at the aortic valve decreased, magnitude of velocity increased first and then decreased. Fig. 2(e-f) showed the velocity distributions at two time points during ejection phase. Fig. 2(e) gave the peak of velocity magnitude during ejection phase.

Figure 2: Flow velocity plots from LV with MI (P3). (a)-(c) give plots during filling phase.One uniform scale was used; (d)-(f) give plots during ejection phase. One uniform scale was used. T=Time, unit: second. Cardiac cycle: [1.54, 2.36], filling phase: [1.54, 2.08];ejection phase: [2.08, 2.36]

Tab. 3 gives the maximum velocity values over the whole LV flow domain at selected time points from the three patients studied. Using the healthy volunteer (P1) data as baseline value, at begin-ejection, velocity magnitude for P2 was 6% higher than that of P1. Velocity magnitude for P3 was 30% lower than that of P1. At begin-filling, velocity magnitude for hypertension patient (P2) was 16% higher than that of P1. Velocity magnitude for infarcted patient (P3) was 22% lower than that of P1. At the peak of filling, velocity magnitude for P1 and P2 were similar. Velocity magnitude for infarcted patient (P3) was 5% lower than that of P1. At the peak of ejection, velocity magnitude for P2 was 5% higher than that of P1. Velocity magnitude for P3 was 8% lower than that of P1. This indicated the velocity magnitude from hypertension patient was higher than that from healthy volunteer.Moreover, the velocity magnitude from healthy volunteer were higher than that from infarcted patient.

Table 3: Velocity, vorticity and flow maximum shear stress (FSS) at four significant timepoints from three patients. Note: velocity used the maximum value over entire LV flow domain. Vorticity used the average value over entire LV flow domain. AFSS used average FSS value on LV inner surface

3.2 Infarcted LV had higher vorticity and smaller vortex area

In addition to flow velocity, vorticity (the curl of the velocity field) is another major flow characteristics worthy investigating. Flow vortex pattern can be analyzed at critical time points. Using flow velocity distribution, we can find the location and shape of the vortex.The contour lines of vorticity allow us to identify vortices and their shape and structures.Table 3 gives the average vorticity values in LV chamber at selected time points from the three patients. Using the value of healthy volunteer as the baseline value, at begin-filling,vorticity magnitude for P2 were 11% lower than that of P1. At peak of ejection, vorticity magnitude for P2 and P3 were 24% and 109% higher than that of P1, respectively. At peak of filling, vorticity magnitude for P2 and P3 were also higher than that of P1 (13% and 42%). The differences were smaller at other time points.

For the evaluation of the vortex, the area of vorticity＞0 is defined as the vortex area. Fig.3 shows the vorticity distribution at end of filling from three patients. The vortex area is 24.23 cm2, 21.33 cm2, 19.73 cm2for P1, P2, and P3, respectively. The vortex area for P3 was 19% smaller than that of P1. The vortex area for P2 was 12% smaller than that of P1.

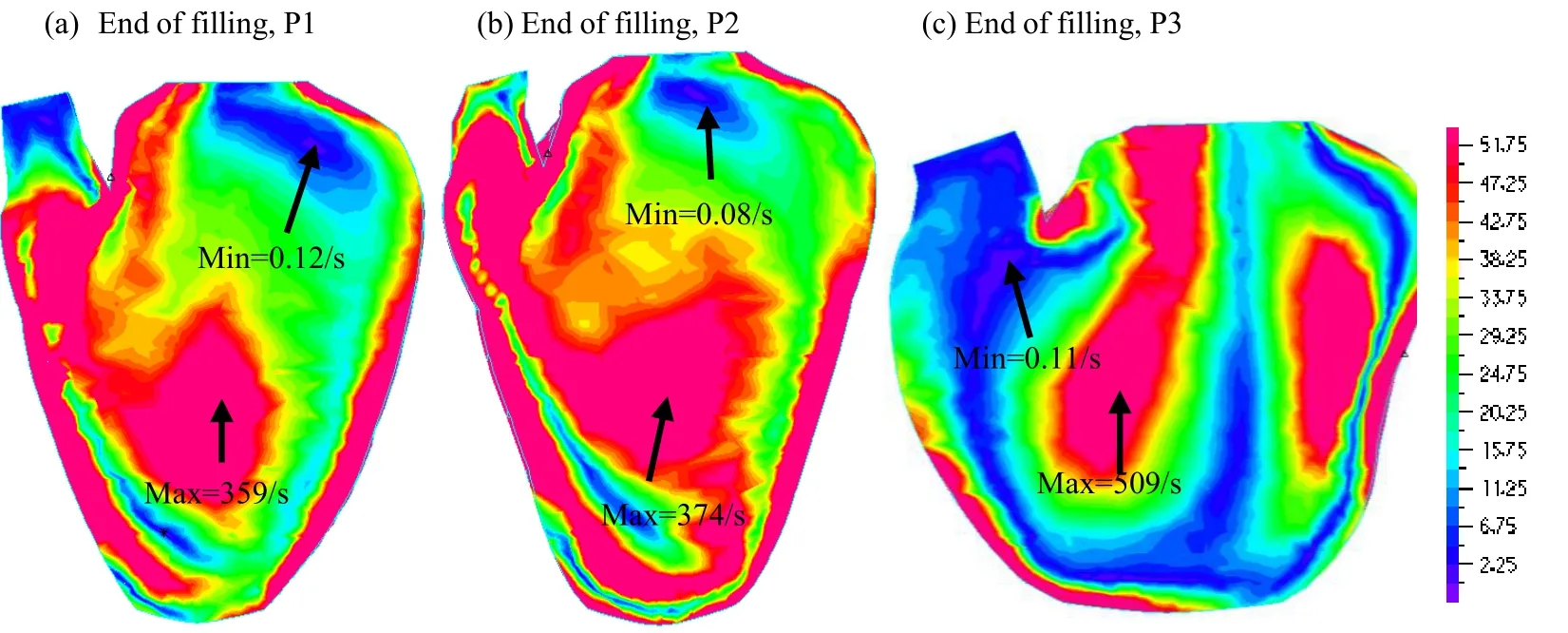
Figure 3: Vorticity distribution at the end of filling from three patients

3.3 Hypertension LV had higher maximum FSS and MI LV had lower maximum FSS at inlet/outlet

Flow shear stress (FSS) reflects the influence of flow on LV inner surface and ventricle valves. Because FSS may be linked to ventricle and valves disease initiation and development, surgical treatment, valve design and placement, tissue engineering and tissue regeneration strategies, it has been a hot topic for cardiovascular investigations. Our current models did not include valve mechanics. Therefore, we investigated FSS on LV inner surface. It is worth noting that FSS has different values following different directions on the LV inner surface, flow maximum shear stress (still referred to as FSS as commonly seen in the literature) was chosen for analysis. Average FSS (AFSS) on LV inner contour for the three patients are summarized in Tab. 3. Using the value of healthy volunteer as the baseline value, at begin-filling, AFSS for P2 and P3 were 58% and 10% higher than that of P1, respectively. At the peak of filling, FSS for P2 and P3 were 54% higher and 48%lower than that of P1, respectively. The differences were smaller at other time points. Fig.4 gave FSS plots of the infracted patient at several point in a cardiac cycle. It can be seen that FSS has its maximum at the inlet of flow during the filling phase and at the outlet of flow during the ejection phase.

Since flow shear stress is of special importance for valve disease formation and progression,Tab. 4 gave the maximum of FSS at the inlet/outlet of flow. At the peak of filling,maximum FSS for P2 was 390% higher than that of P1, the maximum of FSS for P3 was 63% lower than that of P1. It indicated P2 had more higher the maximum of FSS than P1 and P3. At begin of ejection, the maximum of FSS for P2 was 93% higher than that of P1,the maximum of FSS for P3 was 81% lower than that of P1. It should be noted that global FSS occurred near the mitral and aortic valve area, as expected.

Table 4: The maximum of FSS (dyn/cm2) at the inlet/outlet of left ventricle

Figure 4: Flow maximum shear stress in a cardiac cycle from LV with MI (P3)

3.4 LV with MI had lower stress/strain and hypertension LV had higher stress/strain

Ventricle stress and strain are good measure about how hard ventricle muscle is working,it is of interest to calculate LV stress/strain conditions for comparisons. Comparison of average stress and strain values on LV inner contours of FSI models were given in Tab. 5.Using the value of healthy volunteer as the baseline value, at peak of filling, stress and strain of P2 were 41% and 15% higher than those of P1, respectively. Stress and strain of P3 were 36% and 42% lower than those of P1, respectively. At peak of ejection, stress and strain of P2 were 79% and 25% higher than those of P1, respectively. Stress and strain of P3 were 46% and 88% lower than those of P1, respectively. It indicated that P2 has higher stress/strain than P1 and P3 has lower stress/strain than P1. Fig. 5 presents LV stress and strain plots from the infarcted patient showing its patterns at 4 critical time points.

Table 5: Stress and Strain comparison of three patients. Note: Stress and Strain used the average values on LV inner surfaces

Figure 5: Stress-P1 and Strain-P1 plots from LV with MI (P3)

4 Discussion and conclusion

4.1 Significance of the FSI models

Correct ventricle flow characteristics and stress/strain calculations are of fundamental importance for many cardiovascular research where mechanical forces play a role in disease initiation, progression and treatment strategy selections. Ventricle remodeling,disease development, tissue regeneration, patient recovery after surgery and many other cell biological activities are closely associated with ventricle mechanical conditions. FSI models provide complete mechanical analysis including both flow forces and structural stress/strain conditions and fluid structure interaction. FSI models can provide flow-related information, such as flow velocity, vorticity, and shear stress which lack in structure-only models. Our paper provided detailed flow velocity, flow shear stress, and vorticity information and comparisons among LV with MI, LV with hypertension and healthy patient. Those informations fill a gap in the current literature.

4.2 Insight and observations from our three cases

Ventricle flow behaviors are stress/strain conditions are closely linked to ventricle deformation and pressure conditions. Ventricle deformation is reflected by its ejection fraction (EF) i.e. relative ventricle volume is changed in a cardiac cycle. A 50% EF indicates 100% volume increase for its minimum volume to its maximum volume.Everything being equal, larger EF means larger volume change, more flow in and out of LV, higher flow velocity, shear stress, and higher stress/strain at expanded state. The EF rates for the healthy, MI, hypertension cases were 58.6%, 68.5% and 40.4%, respectively.So the hypertension case had higher peak velocity, shear stress and LV stress/strain. The MI case had lower peak velocity, shear stress and LV stress/strain. Since ventricle with infarct lost some contracting ability (infarct tissue is not able to contract), its cardiac function is adversely affected.

4.3 Model limitations

Model limitations include the following: a) ventricle valve mechanics was not included.Valve mechanics plays an important role. However, including it requires considerable more data (valve morphology and material properties) and it remains to be our future modeling effort; b) local ventricle deformation imaging data (by particle tracking) was not included;such data will be very useful for determining tissue material properties and infarct area; c)active contraction and expansion were modeled by material stiffening and softening without adjusting zero-stress ventricle geometries.

Acknowledgement: This research was supported in part by National Sciences Foundation of China grants 11672001, 81571691, 81771844. Longling Fan’s research is supported in part by the Fundamental Research Funds for the Central Universities (KYLX15_0110) and the Scientific Research Foundation of Graduate School of Southeast University(YBJJ1617).

Arefin, M. S.; Morsi, Y. S. (2014): Fluid structure interaction (FSI) simulation of the left ventricle (LV) during the early filling wave (E-wave), diastasis and atrial contraction wave (A-wave). Australasian Physical & Engineering Sciences in Medicine, vol. 37, pp. 413-423.

Axel, L. (2002): Biomechanical dynamics of the heart with MRI. Annual Review of Biomedical Engineering, vol. 4, pp. 321-347.

Baccani, B.; Domenichini, F.; Pedrizzetti, G.; Tonti, G. (2002): Fluid dynamics of the left ventricular filling in dilated cardiomyopathy. Journal of Biomechanics, vol. 35, pp.665-671.

Bathe, K. J. (1996): Finite element procedures. Prentice Hall, Inc., New Jersey.

Bathe, K. J., Eds, (2002): Theory and modeling guide, Vol I & II: ADINA and ADINAF, ADINA R & D, Inc., Watertown, MA, USA.

Bathe, K. J.; Ledezma, G. A. (2007): Benchmark problems for incompressible fluid flows with structural interactions. Computers & Structures, vol. 85, pp. 628-644.

Bathe, K. J.; Zhang, H. (2004): Finite element developments for general fluid flows with structural interactions. International Journal for Numerical Methods in Engineering, vol.60, pp. 213-232.

Chahboune, B.; Crolet, J. M. (1998): Numerical simulation of the blood-wall interaction in the human left ventricle. The European Physical Journal-Applied Physics, vol. 2, pp.291-297.

Chan, B. T.; Lim, E.; Chee, K. H.; Abu Osman, N. A. (2013): Review on CFD simulation in heart with dilated cardiomyopathy and myocardial infarction. Computers in Biology and Medicine, vol. 43, no. 4, pp. 377-385.

Cheng, Y.; Oertel, H.; Schenkel, T. (2005): Fluid-structure coupled CFD simulation of the left ventricular flow during filling phase. Annals of Biomedical Engineering, vol. 33,pp. 567-576.

Delemarre, B. J.; Visser, C. A.; Bot, H.; Dunning, A. J. (1990): Prediction of apical thrombus formation in acute myocardial infarction based on left ventricular spatial flow pattern. Journal of the American College of Cardiology, vol. 15, no. 2, pp. 355-360.

Doenst, T.; Spiegel, K.; Reik, M.; Markl, M.; Hennig, J. et al. (2009): Fluid-dynamic modeling of the human left ventricle: methodology and application to surgical ventricular reconstruction. Annals of Thoracic Surgery., vol. 87, no. 4, pp. 1187-1195.

Domenichini, F.; Pedrizzetti, G. (2011): Intraventricular vortex flow changes in the infarcted left ventricle: numerical results in an idealised 3D shape. Computer Methods in Biomechanics and Biomedical Engineering, vol. 14, no. 1, pp. 95-101.

Fan, L. L.; Yao, J.; Yang, C.; Tang, D.; Xu, D. (2015): Infarcted left ventricles have stiffer material properties and lower stiffness variation: 3D echo-based modeling to quantify in vivo ventricle material properties. Journal of Biomechanical Engineering, vol.137, no. 8.

Fan, L. L.; Yao, J.; Yang, C.; Tang, D.; Xu, D. (2016): Modeling active contraction and relaxation of left ventricle using different zero-load diastole and systole geometries for better material parameter estimation and stress/strain calculations. Molecular & Cellular Biomechanics, vol. 13, no. 1, pp. 44-68.

Fan, R.; Yao, J.; Yang, C.; Tang, D.; Xu, D. (2014): 3D echo-based patient-specific computational left ventricle models to quantify material properties and stress/strain differences between ventricles with and without Infarct. Computer Modeling in Engineering and Sciences, vol. 99, no. 6, pp. 491-508.

Holzapfel, G. A.; Gasser, T. C.; Ogden, R. W. (2000): A new constitutive framework for arterial wall mechanics and a comparative study of matereial models. Journal of Elasticity,vol. 61, pp. 1-48.

Humphrey, J. D. (2002): Cardiovascular solid mechanics. Springer-Verlag, New York.

Hunter, P. J.; Pullan, A. J.; Smaill, B. H. (2003): Modeling total heart function. Annual Review of Biomedical Engineering, vol. 5, pp. 147-177.

Imanparast, A.; Fatouraee, N.; Sharif, F. (2017): Comprehensive computational assessment of blood flow characteristics of left ventricle based on in-vivo MRI in presence of artificial myocardial infarction. Mathematical Biosciences, vol. 294, pp. 143-159.

Khalafvand, S. S.; Ng, E. Y.; Zhong, L.; Hung, T. K. (2012): Fluid-dynamics modelling of the human left ventricle with dynamic mesh for normal and myocardial infarction:preliminary study. Computers in Biology and Medicine, vol. 42, no. 8, pp. 863-870.

Khalafvand, S. S.; Zhong, L.; Ng, E. Y. (2014): Three-dimensional CFD/MRI modeling reveals that ventricular surgical restoration improves ventricular function by modifying intraventricular blood flow. Journal for Numerical Methods in Biomedical Engineering,vol. 30, no.10, pp. 1044-1056.

Lemmon, J. D.; Yoganathan, A. P. (2000): Computational modeling of left heart diastolic function: examination of ventricular dysfunction. Journal of Biomechanical Engineering,vol. 122, no. 4, pp. 297-303.

Long, Q.; Merrifield, R.; Xu, X. Y.; Kilner, P.; Firmin, D. N. et al. (2008): Subjectspecific computational simulation of left ventricular flow based on magnetic resonance imaging. Proceedings of the Institution of Mechanical Engineers, Part H., vol. 222, no. 4,pp. 475-485.

Mangual, J. O.; Kraigher-Krainer, E.; De Luca, A.; Toncelli, L.; Shah, A. et al. (2013):Comparative numerical study on left ventricular fluid dynamics after dilated cardiomyopathy.Journal of Biomechanics, vol. 46, no. 10, pp. 1611-1617.

McCulloch, A. M.; Waldman, L.; Rogers, J.; Guccione, J. (2007): Continuity 6 (a package distributed free by the National Biomedical Computation Resource). www.continuity.ucsd.edu.McCulloch, A. M.; Waldman, L.; Rogers, J.; Guccione, J. (1992): Large-scale finite element analysis of the beating heart. Critical Review in Biomedical Engineering, vol. 20,no. 5-6, pp. 427-449.

McQueen, D. M.; Peskin, C. S. (2000): A three-dimensional computer model of the human heart for studying cardiac fluid dynamics. ACM SIGGRAPH Computer Graph, vol.34, no. 1, pp. 56-60.

Peskin, C. S. (1977): Numerical analysis of blood flow in the heart. Journal of Computational Physics, vol. 25, pp. 220-252.

Saber, N. R.; Gosman, A. D.; Wood, N. B.; Kilner, P. J.; Charrier, C. L. et al. (2001):Computational flow modeling of the left ventricle based on in vivo MRI data: initial experience. Annals of Biomedical Engineering, vol. 29, no. 4, pp. 275-283.

Sacks, M. S.; Chuong, C. J. (1993): Biaxial mechanical properties of passive right ventricular free wall myocardium. Journal of Biomechanical Engineering, vol. 115, pp.202-205.

Tang, D.; Yang, C.; Geva, T.; del Nido, P. J. (2007): Two-layer passive/active anisotropic FSI models with fiber orientation: MRI-based patient-specific modeling of right ventricular response to pulmonary valve insertion surgery. Molecular & Cellular Biomechanics, vol. 4, no. 3, pp. 159-176.

Tang, D.; Yang, C.; Geva, T.; del Nido, P. J. (2008): Patient-specific MRI-based 3D FSI RV/LV/patch models for pulmonary valve replacement surgery and patch optimization.Journal of Biomechanical Engineering, vol. 130, no. 4.

Tang, D.; Yang, C.; Geva, T.; del Nido, P. J. (2010b): Image-based patient-specific ventricle models with fluid-structure interaction for cardiac function assessment and surgical design optimization. Progress in Pediatric Cardiology, vol. 30, no. 1-2, pp. 51-62.

Tang, D.; Yang, C.; Geva, T.; Gaudette, G.; del Nido, P. J. (2010a): Effect of patch mechanical properties on right ventricle function using MRI-based two-layer anisotropic models of human right and left ventricles. Computer Modeling in Engineering & Sciences,vol. 56, no. 2, pp. 113-130.

Tang, D.; Yang, C.; Geva, T.; Gaudette, G.; del Nido, P. J. (2011): Multi-physics MRI-based two-layer fluid-structure interaction anisotropic models of human right and left ventricles with different patch materials: cardiac function assessment and mechanical stress analysis. Computers & Structures, vol. 89, pp. 1059-1068.

Tang, D.; Zuo, H.; Yang, C.; Wu, Z.; Huang, X. et al. (2017): In vivo MRI-based models to quantify right ventricle morphological and mechanical characteristics for healthy and patients with tetralogy of fallot. Molecular & Cellular Biomechanics, vol. 14, no. 3, pp.137-151.

Taylor, T. W.; Okino, H.; Yamaguchi, T. (1994): Three-dimensional analysis of left ventricular ejection using computational fluid dynamics. Journal of Biomechanical Engineering, vol. 116, no. 1, pp. 127-130.

Vierendeels, J. A.; Riemslagh, K.; Dick, E.; Verdonck, P. R. (2000): Computer simulation of intraventricular flow and pressure during diastole. Journal of Biomechanical Engineering, vol. 122, pp. 667-674.

Watanabe, H.; Sugiura, S.; Kafuku, H.; Hisada, T. (2004): Multiphysics simulation of left ventricular filling dynamics using fluid-structure interaction finite element method.Biophysical Journal, vol. 87, no. 3, pp. 2074-2085.

Yang, C.; Tang, D.; Yuan, C.; Kerwin, W.; Liu, F. et al. (2008): Meshless generalized finite difference method and human carotid atherosclerotic plaque progression simulation using multi-year MRI patient-tracking data. Computer Modeling in Engineering &Sciences, vol. 28, no. 2, pp. 95-107.

Zuo, H.; Tang, D.; Yang, C.; Gaudette, G.; Billiar, K. L. et al. (2015): 3D fluid-structure interaction canine heart model with patch to quantify mechanical conditions for optimal myocardium stem cell growth and tissue regeneration. Molecular & Cellular Biomechanics,vol. 12, no. 2, pp. 67-85.