Dimensionless Study on Secretion Clearance of a Pressure Controlled Mechanical Ventilation System with Double Lungs

Dongkai Shen, Qian Zhang Yixuan Wang, Huiqing Ge and Zujin Luo

1 Introduction

Mechanical ventilation is an important treatment in intensive care units for patients who cannot breathe adequately on their own [Wang, Mahfouf, Mills et al. (2010); Williams,Hinojosa-Kurtzberg and Parthasarathy (2010); Shi, Niu, Cai et al. (2015)]. In recent years,there has been rapid development in mechanical ventilation systems, and studies of the respiratory system refer to various approaches for clinical diagnosis and treatment [Ionescu,Derom and Keyser (2010); Chmielecki, Foo, Oxnard et al. (2011); Shi, Niu, Cao et al.(2015); Koc, King, Teschl et al. (2011); Szaleniec, Składzień, Tadeusiewicz et al. (2012);Sturm (2011)]. Due to the establishment of an artificial endotracheal tube, the movement of patients’ mucosa cilia is restrained, resulting in muco-ciliary impairment with ineffective secretion clearance and leaking of subglottic secretions through the tube cuff. Furthermore,due to the use of sedatives and muscle relaxants, the patients are unable to cough whilst they are comatose [Shi, Zhang, Wang et al. (2016); Katori and Tsukuda (2005); Guldfred,Lyhne and Becker (2008); Gerber and Robinson (2007); Rose and Hanlon (2011)].

As a result, the expectoration capacity of ventilated patients continues to decline and may even disappear [Shi, Niu, Cai et al. (2015); Feltracco, Falasco, Barbieri et al. (2011);Avinash and Carli (2008)]. In addition, secretions deposited in the patient’s airway aggravate hypoxia and carbon dioxide retention [Dyhr, Bonde and Larsson (2003);Maggiore, Lellouche, Pigeot et al. (2003); Munnur, Bandi and Gropper (2009)], and may result in bacteria-collecting which can cause the occurrence or aggravation of pulmonary infection and increase patient mortality [Morrissey (2007); Tsoumakidou and Siafakas(2006); Huh, Fujioka, Tung et al. (2007); Safdar, Crnich and Maki (2005); Branson (2007);Hess (2005)]. Hence secretion clearance is an important nursing measure [Redlarski and Jaworski (2013); Eyles and Pimmel (1981); Diong, Goldman and Nazeran (2011);Vassiliou, Amygdalou, Psarakiset al. (2003)], and it is relevant to study the modelling of the secretion clearance function.

Most of these systems are complex and changeable, and the influence of individual parameters on the whole system is difficult to analyze. Some dynamic characteristics and properties of the respiratory system cannot be measured directly. In the case of a multiparameter mechanical ventilation system, the research method is very important. The use of a dimensionless model allows the system to be simplified to permit and analysis of the impact of each parameter on the system.

There are a number of studies of mechanical ventilation systems with a secretion clearance function but these are based on a single lung and an electric model [Branson, Johannigman,Campbell et al. (2002); Chatburn and Mireles-Cabodevila (2011); Tehrani (2008)], which are only approximately equivalent to the human respiratory systems. These studies are not consistent with the actual situation as there are two lungs in the human respiratory system,and hence the reliability and applicability of these studies is limited and they cannot be used for clinical practice and treatment. Hence the development of a mathematical model of a mechanical ventilation pneumatic system with double lungs is helpful to promote the development of mechanical ventilation system research, and can be safely and effectively applied to clinical treatment.

In this paper, a dimensionless pneumatic mathematical model of a mechanical ventilation system of double lungs with a secretion clearance function is built. An experiment with a ventilator in pressure controlled ventilation mode is also constructed. The experimental data is compared with the simulation data to verify the mathematical model. The simulation model is then used to obtain data to analyze the influence of each parameter on the coupling of the two lungs. Finally, the impact of each parameter on the respiratory system is obtained by fitting the orthogonal experiment data.

2 Introduction of mechanical ventilation system of double lungs

Modern mechanical ventilation technology is developing rapidly. The most widely used system is positive pressure mechanical ventilation, which has many different modalities[Branson, Johannigman, Campbell et al. (2002); Chatburn and Mireles-Cabodevila (2011);Tehrani (2008)], amongst which is Pressure Controlled Ventilation (PCV). This is a classical ventilation model generally used in respiratory failure [Choi, Na, Choi et al.(2011); Karakurt, Yarkin, Altinoz et al. (2009); Chatburn (2004); Borrello (2005); Niu, Shi,Cao et al. (2017)]. Bi-level Positive Airway Pressure (BIPAP) Controlled Ventilation,which is based on PCV, is often used for current clinical treatment. The BIPAP ventilator is small in size and has the advantages of simple and safe operation, flexibility and a reliable curative effect. Hence a BIPAP ventilator is used for this work.

The secretion clearance ventilation system with double lungs is simplified as shown in Fig.1. It consists of a single ventilator with a secretion clearance function, three tracts including the single respiratory airway tract, and two human lungs. This system can also be represented as an equivalent pneumatic system, as shown in Fig. 2.

The ventilator and the pumping unit can be regarded as a compressor and a vacuum pump.The air resistance of the respiratory system can be expressed by three throttle valves. Two variable volume containers represent the two human lungs. The pressure in the system does not exceed 40 cmH2O, so the compliance of tracts and the airway tract can be neglected[Shi, Niu and Cai (2016); Shi, Niu, Cao et al. (2016); Shen, Zhang and Shi (2016)].

Figure 1: Simplified mechanical representation of human ventilation system with secretion clearance function

Figure 2: Equivalent pneumatic system

3 Mathematical modelling of mechanical ventilation system with double lungs

This pneumatic model is used to establish the aerodynamic mathematical equations. The following assumptions are made prior to defining the mathematical model:

1) The gas in the system is an ideal gas;

2) There is no air leakage during the working process;

3) Temperatures remains constant during the working process;

4) Dynamic process of the system is a balanced process;

5) The parameters of the air, such as density, specific heat and so on, remain unchanged throughout.

The value of pd/pu is always greater than b (0.528). Hence the mathematical equations for a mechanical ventilation system with double lungs may be derived [Shi, Zhang, Wang et al. (2016); Shi, Zhang, Cai et al. (2016); Shi, Wang, Cai, (2018); Shi, Ren, Cai et al. (2011);Ren, Shi, Cai et al. (2017); Ren, Cai, Shi et al. (2017); Shi, Wang, Liang et al. (2016); Cai,Wang, Shi et al. (2016)]:

3.1 Mass flow equation

3.2 Volume flow equation

3.3 Pressure equation

3.4 Volume equation

The compliance (C) of the two lungs can be described as:

Hence the volume of the right lung and left lung can be calculated as:

4 Dimensionless model of secretion clearance mechanical ventilation system

According to the above description, there are many parameters for the secretion clearance mechanical ventilation system with double lungs, including 5 ventilator parameters such as the IPAP, EPAP, breaths per minute (BPM), inspiratory time (Ti), and rise time of pressure(Tri). It becomes complex to analyze the system directly. Hence this is simplified by making the system and the system parameters dimensionless. In this way, the multi-parameter mechanical ventilation system becomes simpler and easier to analyze.

As the research object of this paper is double lungs, the parameters of any lung cannot be regarded as the reference of the whole system. Therefore, the total parameters of the whole respiratory system are defined as the reference of the dimensionless system.

During a respiratory cycle, the tidal volume of the system (Vt) is approximately equal to the sum of the left lung (Vlt) and the right lung (Vrt). The same applies to the maximal air mass volume (mmax). The reference air mass flow (qmax) reaches the maximum value for the whole period when the upstream pressure of the throttle valve reaches IPAP and the downstream pressure reaches EPAP.

In addition, the coupling effect between the two lungs of the dimensionless secretion clearance mechanical ventilation system is reflected in the relationship between the dimensionless compliance (C∗) and the resistance (R∗) of the two lungs. According to the structure of the human respiratory system, the lungs are connected in parallel. Compliance (C∗) is in a series relation, and air resistance (R∗) is in a parallel relation. The dimensionless compliance (C∗) and the resistance (R∗) of the two lungs can be get based on Kirchhoff's law.

4.1 Dimensionless compliance

4.2 Dimensionless air resistance

The reference values and the dimensionless variables are shown in Tab. 1.

Table 1: The reference values and the dimensionless variables

4.3 Dimensionless flow equation

As the equivalent effective area Arand Alare the same as Ae, Eq. (21) and (22) can be rewritten as:

4.4 Dimensionless pressure equation

It should be explained that pa∗is the dimensionless atmospheric pressure.

4.5 Dimensionless volume equation

4.6 Dimensionless tidal volume

During one respiratory cycle, the tidal volume (Vt) in the system is equal to the sum of the left lung (Vlt) and the right lung (Vrt). Hence the following equation is obtained:

4.7 Dimensionless peak suction flow

This also applies to the peak suction flow. In a single respiration cycle, the peak suction flow (qp) in the system is equal to that of the left lung (qlp) and the right lung (qrp).

According to the above equations, it is clear that the mathematical model of the dimensionless secretion clearance mechanical ventilation system with double lungs is mainly determined by dimensionless compliance (C*) and dimensionless air resistance (R*)when the ventilator parameters are fixed.

5 Simulation and experimental study on the mechanical ventilation system

5.1 Experimental apparatus

As shown in Fig. 3, an experiment is constructed to verify the mathematical model. The experimental equipment includes a BIPAP ventilator, a pressure-flow sensor which can measure the pressure and flow on two channels, two lung simulators, and medical plastic tubes to connect the ventilator, lung simulators and sensor.

It is important to note that when the suction pressure of the suction unit is set to the value of the expiatory positive airway pressure, the process of secretion clearance is equivalent to a ventilation process. Hence the process of secretion clearance should be treated as a special ventilation process.

The ventilator is a HAMILTON-C2 supplied by HAMILTON MEDICAL Company. It provides different mechanical ventilation modes including the BiPAP mode used in this experiment. The parameters for the ventilator are set at the start of the experiment. The values of IPAP and EPAP are set to 22 cmH2O and 4 cmH2O respectively, the dimensionless value is 1 and 0.9829. The values of Tiand Trare set to 1s and 0.3 s, the dimensionless value is 3.1496 and 0.9449. The BIPAP ventilator provides 20 cycles per minute.

5.2 Simulation of the ventilation system

Using the mathematical equations above, the dimensionless simulation model is established by MATLAB /SIMULATION software. Since the BIPAP ventilator does not have a secretion clearance function, the suction pressure of the simulation model is removed temporarily. The parameters for the lungs are the same, so the experimental data, which is dimensionless, can be compared to any single lung simulation data. The comparison of the dimensionless pressure and flow curves from the experiment with those of the dimensionless simulation are shown in Fig. 4 and Fig. 5.

Figure 3: Experimental apparatus

Figure 4: Curve of dimensionless pressure of one lung

Figure 5: Curve of dimensionless flow in one lung

5.3 Analysis and discussions

The following conclusions can be drawn from Fig. 4 and Fig. 5:

1) The simulation curve is consistent with the experimental curve.

2) The camber of the pressure experiment curve is greater than that of the pressure simulation curve, and the slope of pressure simulation curve is larger. This can be attributed to a delay in the response time.

3) The maximum and minimum values of the simulation curve and the experimental curve are the same. The maximum value of the dimensionless pressure is about 1,which is the dimensionless IPAP, and the minimum value is about 1, which is the dimensionless EPAP. Because both the reference of IPAP and EPAP are the maximum of them. The experimental parameters of the ventilator settings are in agreement with the experimental curves. Hence the experimental data is safe and reliable.

The experimental design is correct because the experimental data is reliable. Therefore, the simulation model and the mathematical model are correct and reliable.

6 Working characteristics of the secretion clearance ventilation system with double lungs

6.1 Influence of dimensionless compliance and dimensionless air resistance on secretion clearance ventilation system

According to the description of the mathematical model, dimensionless compliance (C*)and dimensionless air resistance (R*) play an important role in the ventilation system. In addition, the coupling between the two lungs is reflected in C*and R*, which is based on Eqs. (16) and (20). When the value of C*or R*is changed for one of the lungs, the corresponding value of C*or R*for the other lung also changes. Under normal conditions,the basic value of C for both lungs is set to 10 mL/cmH2O, and the basic value of R is set to 6 cmH2O/L/s. In this way, the maximum value of lung pressure can just reach IPAP [Niu,Shi, Cao et al. (2017); Shi, Niu, Cai et al. (2016)]. At this point, Cr*and Cl*are 0.5, and Rr*and Rl*are 2.0. The curves showing the comparison between the normal state and the secretion clearance state are shown in Fig. 6.

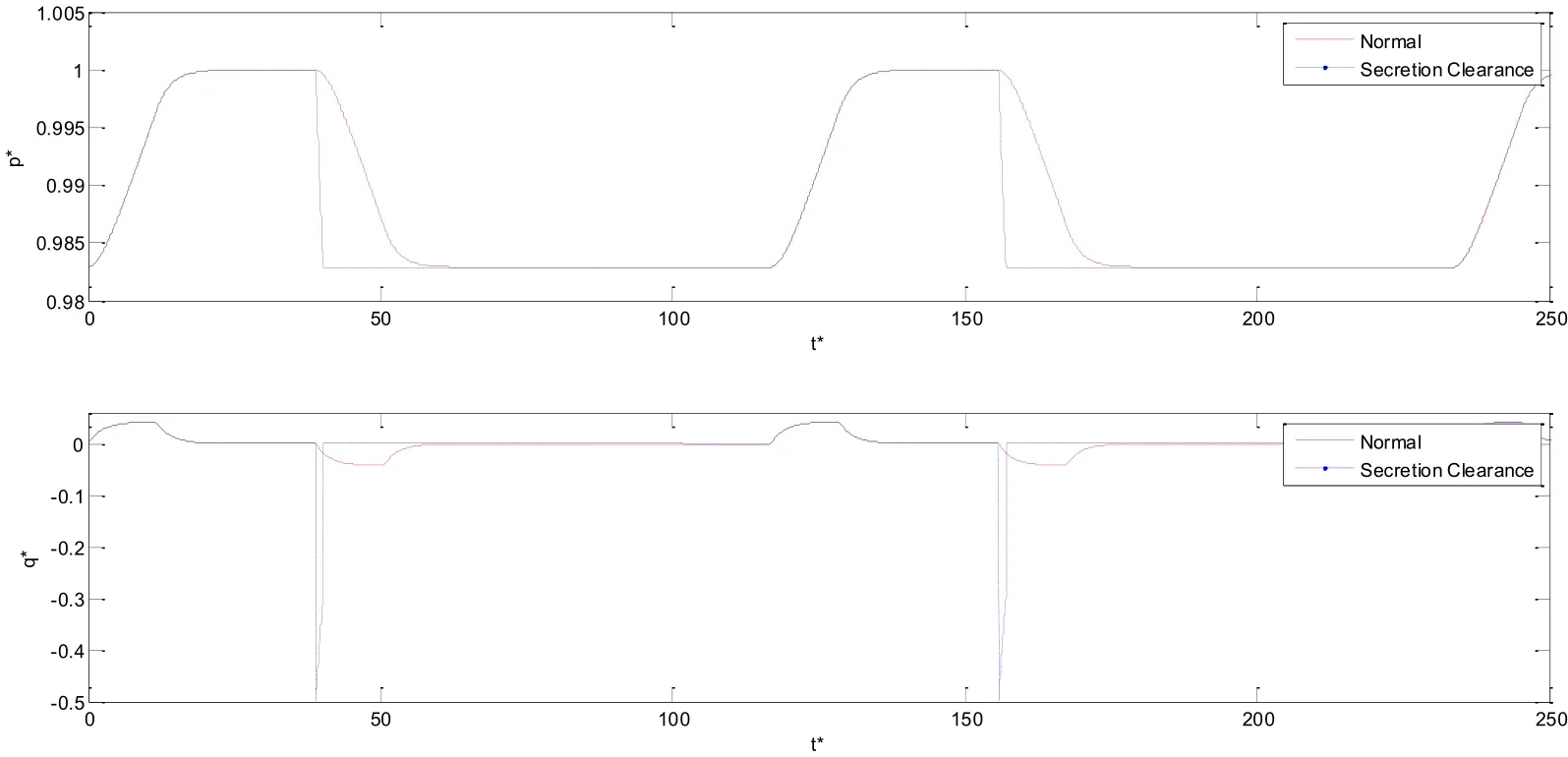
Figure 6: Comparison between normal operation and the secretion clearance function

In Fig. 6, it is obvious that the curve the slope of secretion clearance curve is much larger than that of the normal curve in expiration process. In addition, the time of gas retention in the lung during the secretion clearance state is less than that in the normal state.

6.2 Influence of dimensionless compliance on secretion clearance ventilation system with double lungs

When the value of right lung dimensionless compliance () is set to 0.3333, 0.5000, and 0.6000, the corresponding value for the left lung dimensionless compliance () is 0.6667,0.5000, and 0.4000. The influence of dimensionless compliance on dimensionless pressure(p*) and dimensionless air mass flow () is shown in Fig. 7 and Fig. 8.

In the right lung, with an increase in, the dimensionless time for the respiratory cycle decreases, and the dimensionless time is lower as the dimensionless pressure of the right lung () remains equal to the dimensionless IPAP (pipap*). However, for the left lung, the opposite holds. Asincreases, the dimensionless time of the respiratory cycle increases,and as dimensionless pressure of the left lung () approaches pipap*the dimensionless time also becomes longer. With an increase in, the slope of thecurve becomes more gradual. Whenstayed longer in pipap*than, and stayed in dimensionless EPAP (pepap*) for less than. When, the state is opposite.

Fig. 8 shows that for both lungs, with an increase of C*the peak value of the air mass (q*)also increases. The dimensionless time becomes longer as negative q* returns to 0. With the same condition for the two lungs, when, the positive right lung dimensionless air mass flow () is higher than the positive left lung dimensionless air mass flow (),and when, the positiveis less than the positive.

In Fig. 10, the curve first increases and then decreases. This is because the suction duration is dependent on the lung whose compliance is less. When Cr＞Cl, the suction duration is determined by the left lung. The basic value of the left lung compliance is maintained at 10 mL/cmH2O so the suction duration remains unchanged. However, the time reference (T0)increases with the increase of the dimensionless compliance of the right lung (), so the second part of the curve shows a decline.

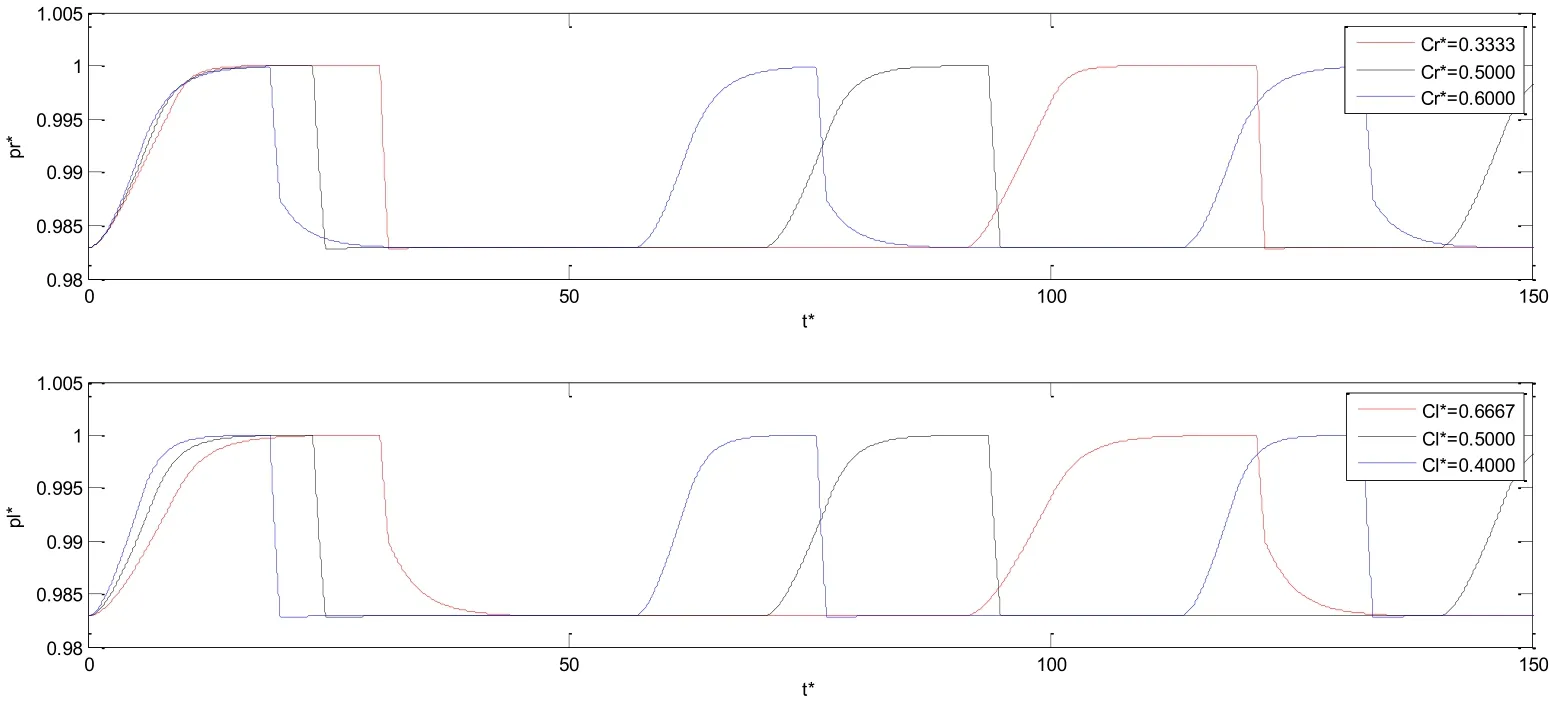
Figure 7: Influence of dimensionless compliance on dimensionless pressure of two lungs

Figure 8: Influence of dimensionless compliance on dimensionless air mass flow of two lungs

Figure 9: Influence of right lung dimensionless compliance on dimensionless peak suction flow

Figure 10: Influence of right lung dimensionless compliance on dimensionless suction duration

6.3 Influence of dimensionless air resistance on secretion clearance ventilation system with double lungs

According to Eq. (20), when the value of right lung dimensionless air resistance () is set to 1.6667, 2.0000 and 2.3333, the value of the left lung dimensionless air resistance () is 2.50, 2.00 and 1.75. The influence of dimensionless air resistance (R*) on dimensionless pressure (p*) and dimensionless air mass flow (q*) is shown in Fig. 11 and Fig. 12.

Fig. 14 shows that the curve representing dimensionless suction duration () increases with an increase in, untilreaches 2.0, which means. When, the curve fordecreases with increasing. The suction duration is determined by the lung with least air resistance. When, the suction duration remains unchanged due to the constant air resistance of the left lung. As the time reference rises with the increase of dimensionless air resistance of right lung (), the second half of the curve is falling.

Figure 11: Influence of dimensionless air resistance on dimensionless pressure of two lungs

Figure 12: Influence of dimensionless air resistance on dimensionless air mass flow of two lungs

Figure 13: Influence of dimensionless air resistance on dimensionless peak suction flow of two lungs

Figure 14: Influence of dimensionless air resistance on dimensionless suction duration

6.4 Orthogonal experiment

In order to study the working characteristics of the secretion clearance mechanical ventilation system with double lungs further, an orthogonal experiment is constructed to analyse multi-factor and multi-level systems. This is more representative and offers the possibility of reducing the work involved.

In accordance with Eq. (16) and Eq. (20), the parameters of each of the lungs are changed.Hence the dimensionless compliance of the right lung (Cr*) and dimensionless air resistance of the right lung (Rr*) are selected as two of the orthogonal experimental factors. The other factors are the dimensionless EPAP (pepap*) and the dimensionless suction pressure (ps*).Each parameter takes 5 different values. The values of the parameters and the orthogonal experimental design are shown in Tab. 2 and Tab. 3.

Table 2: Parameters value for orthogonal experimental design

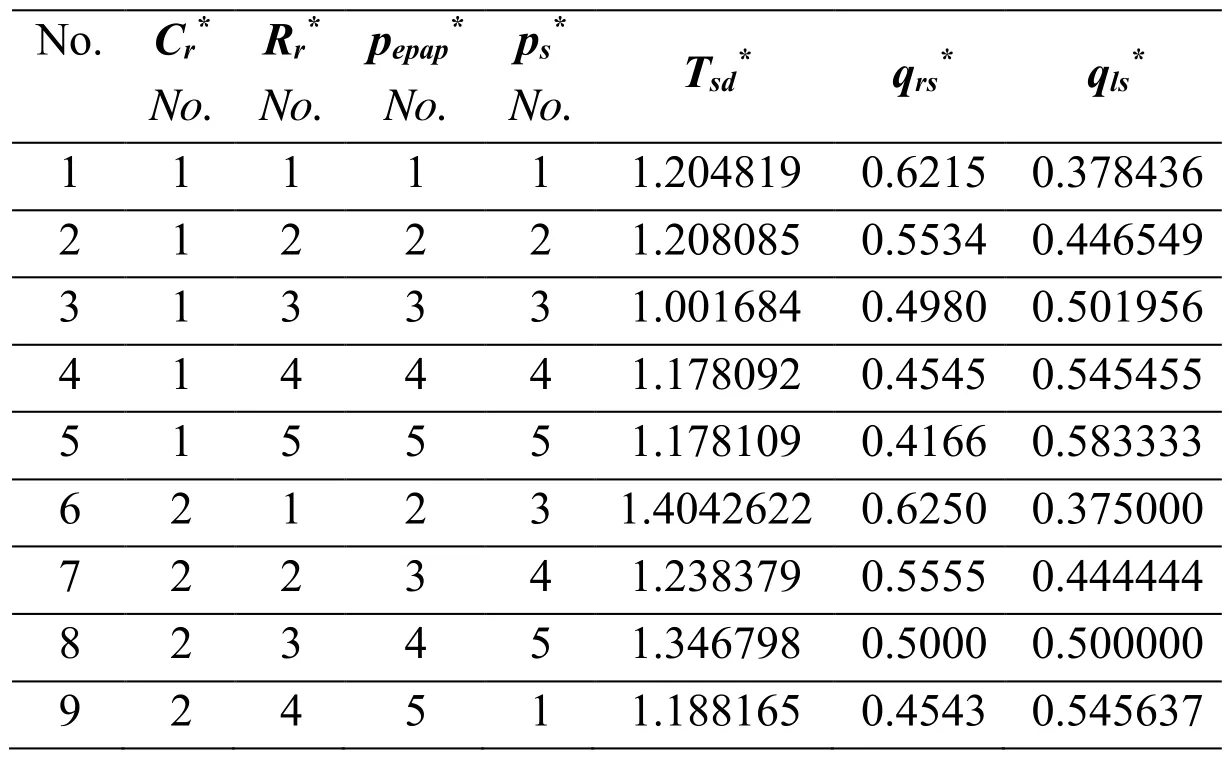
Table 3: Orthogonal experimental design table

10 2 5 1 2 1.509529 0.4165 0.583415 11 3 1 3 5 1.291465 0.6250 0.375000 12 3 2 4 1 1.254352 0.5555 0.444444 13 3 3 5 2 1.044683 0.4999 0.500084 14 3 4 1 3 1.270445 0.4530 0.546918 15 3 5 2 4 1.142631 0.4151 0.584887 16 4 1 4 2 1.230090 0.6249 0.375041 17 4 2 5 3 0.980130 0.5553 0.444614 18 4 3 1 4 1.183508 0.4987 0.501250 19 4 4 2 5 1.015568 0.4514 0.548572 20 4 5 3 1 0.811423 0.4109 0.589096 21 5 1 5 4 1.006985 0.6249 0.375026 22 5 2 1 5 1.163268 0.5544 0.445577 23 5 3 2 1 0.984196 0.4962 0.503739 24 5 4 3 2 0.741525 0.4478 0.552182 25 5 5 4 3 0.713704 0.4078 0.592146

The standard deviation of each factor is calculated by comparing the factors of the orthogonal experiment with the data for each level. The results of the orthogonal experiment are shown in Fig. 15 and Fig. 16. After finishing the orthogonal experiment,the standard deviation of each parameter for dimensionless suction duration () and dimensionless peak suction flow () are calculated. According to Eq. (30), the standard deviation of the dimensionless peak suction flow of the right lung () is the same as the dimensionless peak suction flow of the left lung (). Hence the calculation is done for the standard deviation of one lung qrs*.

When compared with other parameters, the dimensionless air resistance (R*) plays the most important role on both research objects, especially for dimensionless peak suction flow(). In Fig. 15, apart from the dimensionless air resistance (R*), the dimensionless compliance also has a great influence on the dimensionless suction duration. This is dependent on the definition of air resistance. The change of air resistance affects both flow and pressure in the system.

Figure 15: Standard deviation of dimensionless suction duration ()

Figure 16: Standard deviation of dimensionless peak suction flow (

7 Conclusion

This paper provides a novel research method for secretion clearance mechanical ventilation system with double lungs, and a new pneumatic model and mathematical model are established to represent this. The model is used to represent the working characteristics of the system and the coupling effect between the lungs is identified.

The following conclusions can be drawn from this work:

1) The output data of the experiment met the parameters of the ventilator setting and the simulation curves are consistent with the experimental curves. Hence the experimental data and simulation data are in agreement and the simulation model can be applied to further studies of the respiratory system.

2) Changes in the dimensionless compliance (C*) and dimensionless air resistance (R*)do not only change the system's dimensionless respiratory cycle time, but also change the dimensionless suction duration.

3) The relation between dimensionless compliance (C*) and dimensionless peak suction flow () is not a simple linear relationship. There is a boundary condition when the dimensionless compliance of the right lung is equal to that of the left lung(). The relationship between dimensionless air resistance (R*) and dimensionless peak suction flow () can be regarded as inversely proportional.The two parameters are approximately negative inversely proportional.

4) The relationship between the dimensionless suction duration () and the dimensionless compliance of the right lung () are approximately similar to the relationship between the dimensionless suction duration () and the dimensionless air resistance (). These two curves both first rise and then fall. In general, both the suction duration and time reference increase with an increase in compliance or air resistance. In the second part of these two curves, the suction duration remains constant, and the time reference increases. Hence the dimensionless suction duration of the two curves declines.

5) In comparison with other parameters, the dimensionless air resistance (R*) plays the most important role on both dimensionless suction duration () and dimensionless peak suction flow (). The effect of dimensionless compliance (C*)on dimensionless suction duration () is larger than that of the other parameters except for dimensionless air resistance (R*).

However, there are a number of limitations in this study. The mathematical model does not take a number of factors into consideration, namely:

The effects of the ventilator are here analysed specifically in a double-lung model, without taking into account the presence of a chest wall model, with other characteristics, which deeply influence the pressure distribution and the gas mixture flow into the lungs, and can be used in other mechanical ventilation studies and clinical medicine and treatment. The two lungs are represented in a simplified mechanical ventilation system.

Apart from the above mentioned limitations, this novel research method develops a safe and reliable research model is reliable and safe to promote the development of mechanical ventilation technology. It can be applied to other mechanical ventilation studies and in clinical medicine and treatment.

Avinash, S.; Carli, F. (2008): The role of regional anaesthesia in patient outcome: Thoracic and abdominal surgeries. Techniques in Regional Anesthesia & Pain Management, pp. 183-193.

Borrello, M. (2005): Modeling and control of systems for critical care ventilation.

Proceeding of the 2005 American Control Conference, Portland, pp. 2166-2180.

Branson, R. D. (2007): Secretion management in the mechanically ventilated patient.

Respiratory Care, vol. 52, no. 10, pp. 1328-1347.

Branson, R. D.; Johannigman, J. A.; Campbell, R. S.; Jr., D. K. (2002): Closed loop mechanical ventilation. Respiratory Care, vol. 47, pp. 427-451.

Chatburn, R. L. (2004): Computer control of mechanical ventilation. Respiratory Care,vol. 49, pp. 507-515.

Chatburn, R. L.; Mireles-Cabodevila, E. (2011): Closed-loop control of mechanical ventilation: description and classification of targeting schemes. Respiratory Care, vol. 56,no. 1, pp. 85-102.

Chmielecki, J.; Foo, J.; Oxnard, G. R.; Hutchinson, K.; Ohashi, K. et al. (2011):Optimization of dosing for EGFRmutant non-small cell lung cancer with evolutionary cancer modeling. Science Translational Medicine, vol. 3, no. 90, pp. 90ra59.

Choi, E. M.; Na, S.; Choi, S. H.; An, J.; Rha, K. H. et al. (2011): Comparison of volumecontrolled and pressure-controlled ventilation in steep Trendelenburg position for robotassisted laparoscopic radical prostatectomy. Journal of Clinical Anesthesia, vol. 23, no. 3,pp. 183-188.

Cai, M.; Wang, Y.; Shi, Y.; Liang, H. (2016): Output dynamic control of a late model sustainable energy automobile system with nonlinearity. Advances in Mechanical Engineering,vol. 8, no. 11.

Diong, B.; Goldman, M. D.; Nazeran, H. (2011): Respiratory impedance values in adults are relatively insensitiveto mead model lung compliance and chest wall compliance parameters, in Proceedings of the 26th Southern Biomedical Engineering Conference(SBEC’10), pp. 201-203.

Dyhr, T.; Bonde, J.; Larsson, A. (2003): Larsson A, Lung recruitment manoeuvres are effective in regaining lung volume and oxygenation after open endotracheal suctioning in acute respiratory distress syndrome. Critical Care, vol. 7, pp. 55-62.

Eyles, J. G.; Pimmel, R. L. (1981): Estimating respiratory mechanical parameters in parallel compartment models. IEEE Transactions on Biomedical Engineering, vol. 28, pp.313-317.

Feltracco, P.; Falasco, G.; Barbieri, S.; Milevoj, M.; Serra, E. (2011): Anesthetic considerations for nontransplant procedures in lung transplant patients. Journal of Clinical Anesthesia, vol. 23, pp. 508-516.

Gerber, V.; Robinson, N. E. (2007): Airway secretions and mucociliary function. Equine Respiratory Medicine and Surgery, pp. 55-69.

Guldfred, L. A.; Lyhne, D.; Becker, B. C. (2008): Acute epiglottitis: Epidemiology,clinical presentation, management and outcome. Journal of Laryngology & Otology, vol.122, pp. 818-823.

Hess, D. R. (2005): Patient positioning and ventilator-associated pneumonia. Respiratory Care,vol. 50, no. 7, pp. 892-899.

Huh, D.; Fujioka, H.; Tung, Y. C.; Futai, N.; Grotberg, J. B. et al. (2007): Acoustically detectable cellular-level lung injury induced by fluid mechanical stresses in microfluidic airway systems. Proceedings of the National Academy of Sciences of the United States of America, vol. 104, pp. 18886-18891.

Ionescu, C.; Derom E.; Keyser, R. D. (2010): Assessment of respiratory mechanical properties with constant-phase models in healthy and COPD lungs. Computers in Methods Programs Biomed, vol. 97, no. 1, pp. 78-85.

Karakurt, Z.; Yarkin, T.; Altinoz, H.; Atik Güngör, S.; Adigüzel, N. et al. (2009):Pressure vs. volume control in COPD patients intubated due to ARF: a case-control study.Tüberküloz Ve Toraks, vol. 57, no. 2, pp. 145-154.

Katori, H.; Tsukuda, M. (2005): Acute epiglottitis: Analysis of factors associated with airway intervention. Journal of Laryngology & Otology, vol. 12, pp. 967-972.

Koc, H.; King, J.; Teschl, G.; Unterkofler, K.; Teschl, S. et al. (2011): The role of mathematical modeling in VOC analysis using isoprene as a prototypic example. Journal of Breath Research, vol. 5, no. 3, pp. 037102.

Maggiore, S. M.; Lellouche, F.; Pigeot, J.; Taille, S.; Deye, N. et al. (2003): Prevention of endotracheal suctioninginduced alveolar derecruitment in acute lung injury. American Journal of Respiratory & Critical Care Medicine, vol. 167, pp. 1215-1224.

Morrissey, B. M. (2007): Pathogenesis of bronchiectasis. Clinics in Chest Medicine, vol.28, no. 2, pp. 289-296.

Munnur, U.; Bandi, V. D.; Gropper, M. A. (2009): Airway management and mechanical ventilation in pregnancy. Pulmonary Problems in Pregnancy-Respiratory Medicine, pp.385-403.

Niu, J. L.; Shi, Y.; Cao, Z. X.; Cai, M. L.; Chen, W. et al. (2017). Study on air flow dynamic characteristic of mechanical ventilation of a lung simulator. Science China-Technological Sciences, vol. 60, no. 2, pp. 243-250.

Redlarski, G.; Jaworski, J. (2013): A new approach to modeling of selected human respiratory system diseases, directed to computer simulations. Computers in Biology and Medicine, vol. 43, no. 10, pp. 1606-1613.

Rose, L.; Hanlon, G. (2011): Ventilation and Oxygenation Management. ACCCN's Critical Care Nursing, pp. 381-381.

Ren, S.; Cai, M.; Shi, Y.; Xu, W.; Zhang, X. D. (2017): Influence of bronchial diameter change on the airflow dynamics based on a pressure-controlled ventilation system.International Journal for Numerical Methods in Biomedical Engineering, no. 3.

Ren, S.; Shi, Y.; Cai, M.; Xu, W. (2017): Influence of secretion on airflow dynamics of mechanical ventilated respiratory system. IEEE/ACM Transactions on Computational Biology & Bioinformatics, vol. 99, no. 1.

Safdar, N.; Crnich, C. J.; Maki, D. G. (2005): The pathogenesis of ventilator-associated pneumonia: Its relevance to developing effective strategies for prevention. Respiratory Care,vol. 50, no. 6, pp. 725-741.

Shen, D. K.; Zhang, Q.; Shi, Y. (2016): Dynamic characteristics of mechanical ventilation system of double lungs with bi-level positive airway pressure model. Computational and Mathematical Methods in Medicine, vol. 2016, no. 3, pp. 1-13.

Shi, Y.; Niu, J. L.; Cai, M. L.; Xu, W. Q. (2015): Dimensionless study on dynamics of pressure controlled mechanical ventilation system. Journal of Mechanical Science and Technology, vol. 29, pp. 431-439.

Shi, Y.; Niu, J. L.; Cai, M. L.; Xu, W. Q. (2015): Dimensionless optimization study on a ventilator with secretion clearance function. Journal of Mechanics in Medicine & Biology,vol. 15, no. 3.

Shi, Y.; Niu, J. L.; Cai, M. L.; Xu, W. Q. (2016): A respiratory mechanical parameters estimation technology based on extended least squares. Journal of Mechanics in Medicine and Biology, vol. 16, no. 3.

Shi, Y.; Niu, J. L.; Cao, Z. X.; Cai, M. L.; Zhu, J. (2015): Working characteristics of a new ventilator with automatic secretion clearance function. Science China Technological Sciences, vol. 58, pp. 1046-1052.

Shi, Y.; Niu, J. L.; Cao, Z. X.; Cai, M. L.; Zhu, J. et al. (2016): Online estimation method for respiratory parameters based on a pneumatic model. IEEE-Acm Transactions on Computational Biology and Bioinformatics, vol. 13, no. 5, pp. 939-946.

Shi, Y.; Ren, S.; Cai, M. L.; Xu, W.; Deng, Q. (2011): Pressure dynamic characteristics of pressure controlled ventilation system of a lung simulator. Computational and Mathematical Methods in Medicine, vol. 10, pp. 1155-1164.

Shi, Y.; Wang, Y.; Liang, H.; Cai, M. (2016): Power characteristics of a new kind of airpowered vehicle. International Journal of Energy Research, vol. 40, no. 8, pp. 1112-1121.Shi, Y.; Wang, Y.; Cai, M.; Zhang, B.; Zhu, J. (2018): An aviation oxygen supply system based on a mechanical ventilation model. Chinese Journal of Aeronautics, vol. 31, no. 1,pp. 197-204.

Shi, Y.; Zhang, B.; Cai, M.; Zhang, D. (2016): Numerical simulation of volumecontrolled mechanical ventilated respiratory system with two different lungs. International Journal for Numerical Methods in Biomedical Engineering, vol. 33, pp. 2852.

Shi, Y.; Zhang, B. L.; Wang, Z. D.; Cai, M. L.; Shen, D. K. (2016): New Advances in Monitoring and Triggering of Mechanical Ventilation. Science China Technological Sciences, vol. 59, pp. 1791-1792.

Sturm, R. (2011): A computer model for the simulation of ber-cell interaction in the alveolar region of the respiratory tract. Computers in Biology and Medicine, vol. 41, pp.565-573.

Szaleniec, J.; Składzień, J.; Tadeusiewicz, R.; Oleś, K.; Konior, M. et al. (2012): How can an otolaryngologist benet from arti cial neural networks? Otolaryngologia Polska, vol.66, pp. 241-248.

Tehrani, F. T. (2008): Automatic control of mechanical ventilation. Part 2: the existing techniques and future trends. Journal of Clinical Monitoring and Computing, vol. 22, pp.417-424.

Tsoumakidou, M.; Siafakas, N. M. (2006): Novel insights into the aetiology and pathophysiology of increased airway inflammation during COPD exacerbations. Respiratory Research, vol. 7, no. 80, pp. 1186-1465.

Vassiliou, M. P.; Amygdalou, A.; Psarakis, C. J.; Dalavanga, Y.; Vassiliou, P. M. et al.(2003): Volume and flow dependence of respiratory mechanics in mechanically ventilated COPD patients. Respiratory Physiology & Neurobiology, vol. 135, pp. 87-96.

Wang, A.; Mahfouf, M.; Mills, G. H.; Panoutsos, G.; Linkens, D. A. (2010): Intelligent model-based advisory system for the management of ventilated intensive care patients. Part II: Advisory system design and evaluation. Computer Methods and Programs in Biomedicine, vol. 99, pp. 208-217.

Williams, K.; Hinojosa-Kurtzberg, M.; Parthasarathy, S. (2010): Control of breathing during mechanical ventilation: who is the boss? Respiratory Care, vol. 56, pp. 127-139.