关于Smarandache LCM函数的两个性质

杨明顺

(渭南师范学院 数理学院，陕西渭南714099)

定义1［1］对任意正整数n，著名的Smarandache函数S(n)定义为:满足条件n|m!的最小正整数m，即

定义2［1］Smarandache LCM函数SL(n) 定义为:满足条件 n|［1，2，…，k］的最小正整数k，其中:［1，2，…，k］表示 1，2，…，k 的最小公倍数。

定义3 算术函数Ω(n)定义为:Ω(1)=0，当n＞1且n的标准分解式为时，

关于SL(n)的性质，许多学者进行了研究，并获得了很多重要的结果［2－8］。本文利用初等方法及解析方法对的渐近性质进行了深入研究，得到了几个有趣的结论。

1 引理及证明

引理 1［9］设 x ≥ 1，b(n) 是一个数论函数是定义在［x1，xm］(xm＞ x1≥0)上的连续可微函数，则

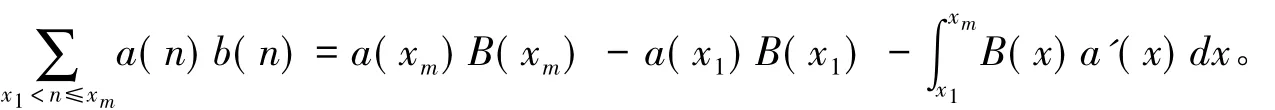
证明 由于a(x)和B(x)都是［x1，xm］上的可微函数，故a(x)、B(x)在［x1，xm］内连续，则在区间［x1，xm］上是可积的。设x1＜x2＜… ＜xm，令

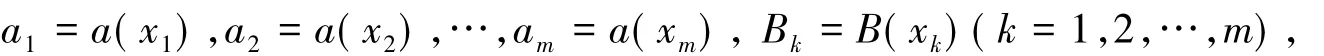
根据微分中值定理，-ξk+1∈ (xk，xk+1)，使得 B(xk+1) － B(xk)=B'(ξk+1)(xk+1－ xk)，所以 -ηk+1∈(xk，xk+1)，有 a(xk+1) － a(xk)=a'(ηk+1)(xk+1－ xk)，则

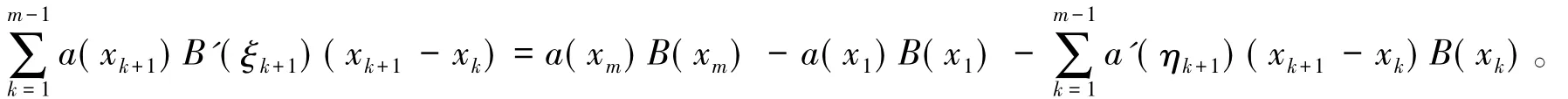
引理2［10］对任意的正整数n，当其标准分解式为时，有

引理3［11］对任意素数p，有 SL(n)=S(n)。

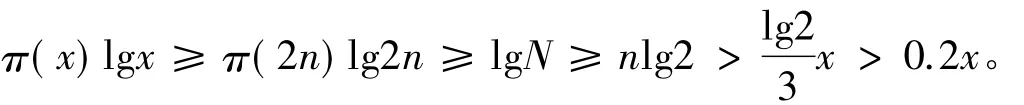
(2)由于(π(2n)－π(n))lgn≤lgN≤2nlg2，把n=2r代入该式即得r(π(2r+1)－π(2r))≤2r+1，由于 π(2r+1)≤2r，故有

任给一个正整数m，在上式中令r=0，1，2，…，m －1，从而得到m个不等式，把它们加起来即得

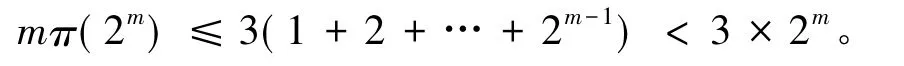
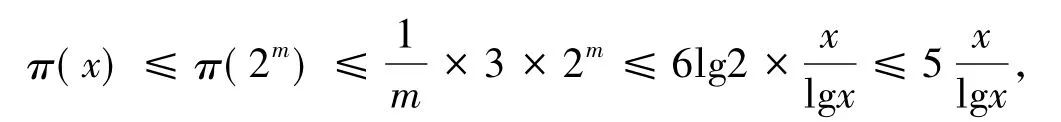
即结论的第二个不等式成立。

推论1［12］当x→∞ 时，不超过x的素数的个数π(x)渐近于

2 结论及证明

证明 经过变形可得

利用函数S( n)及SL( n)的性质以及初等与组合方法来估计式(1)中的误差项。由引理3、引理4有SL( n)－S( n)=0。所以在式(1)的误差项中，所有非0必出现在那些使SL(n)不等于素数的整数n中，即

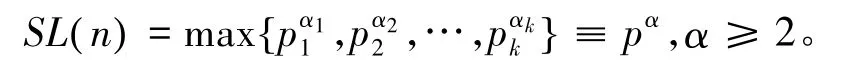
设A为区间 [1 ，x ]中所有满足上式条件 n 的集合，对任意 n ∈ A，设，其中:(p ，n1)=1。现在分两种情况讨论:设A=B+C，其中:n∈B，如果如果于是，有

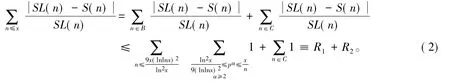
现在分别估计式(2)中的各项，首先估计R1，注意到pα≤ln4x时，有α≤4lnlnx，于是有

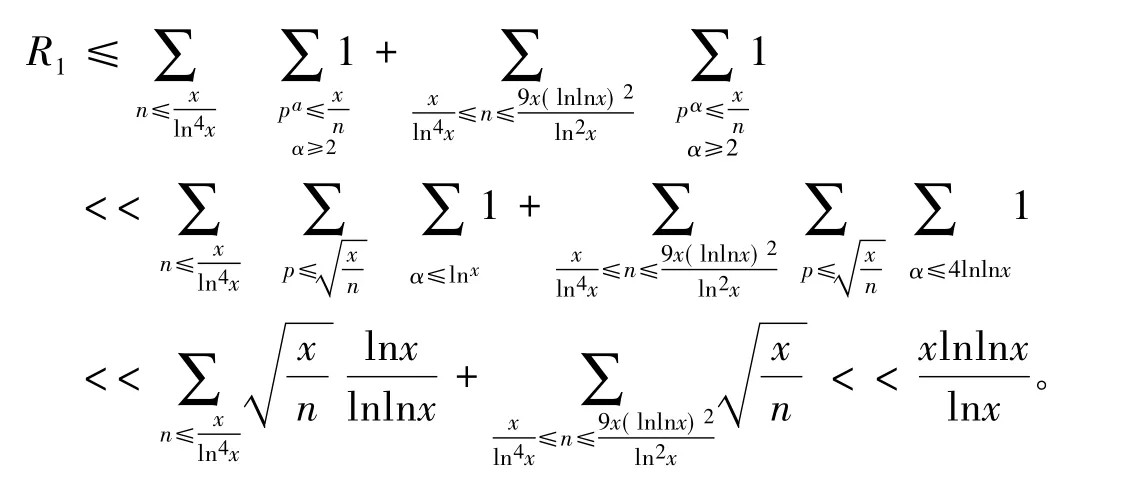
现在估计R2，注意到集合C中包含元素的个数不会超过整数的个数，其中:αi≤2lnlnx，pi于是由素数分布公式有

其中:exp(y)=ey，结合式(2)(3)可推出估计式

定理2 设k≥2是一个给定的整数，那么对任意实数x≥2，有渐近公式

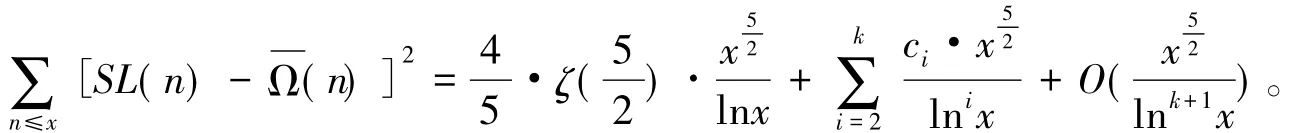
其中:ζ(s) 是 Riemannn 函数，ci(i=1，2，…，k) 是可计算的常数。

其中A包含区间［1，x］中所有那些满足存在素数p，使得p|n且的正整数n;而集合B包含区间［1，x］中所有那些满足n=p1p2p3的正整数n，其中集合C包含区间［1，x］中所有那些满足n=n1p2的正整数n，其中集合D包含区间［1，x］中所有不属于A、B和C的整数n。于是利用引理3的推论及A的定义有

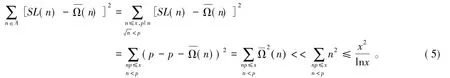
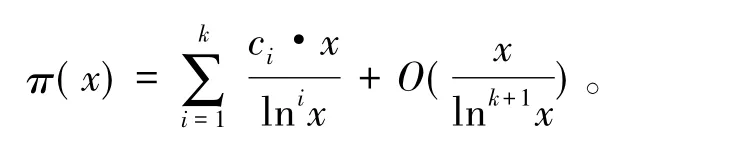
其中:ci(i=1，2，…，k)为常数且c1=1。于是有

应用引理1可得

其中:αi(i=2，3，…，k)为可计算的常数。于是注意到收敛，结合式(7)及式(8)得其中:bi(i=2，3，…，k)为可计算的常数。

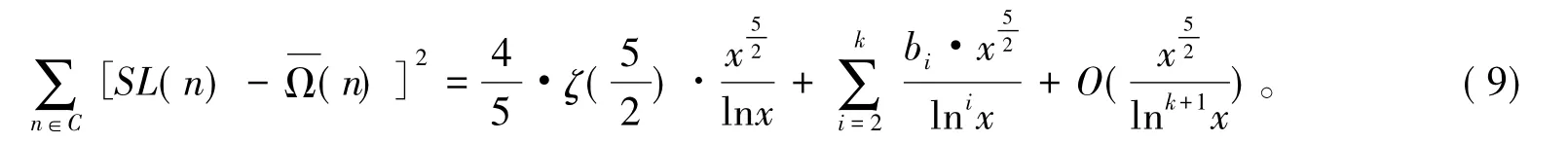
现在讨论集合D中的情况，由式(1)及集合D的定义知对任意n∈D，如果SL(n)=p是一个素数，则如果 SL(n)=p2，则或者SL(n)=pα，α≥3。无论哪种情况都有

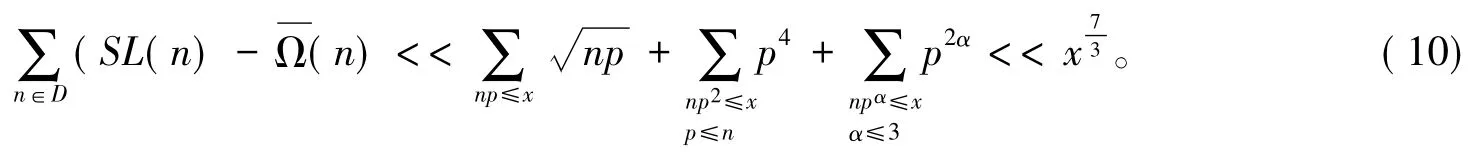
于是结合式(5)(6)(8)(9)可得

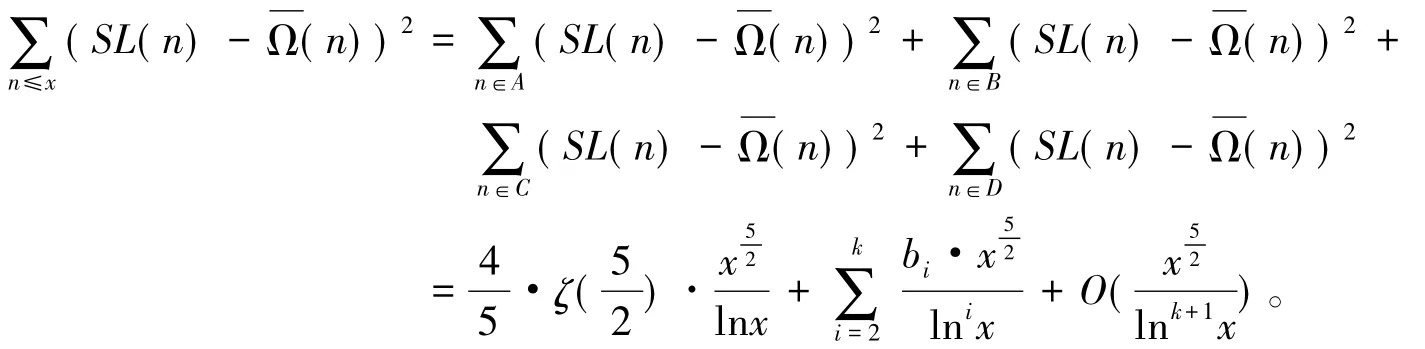
其中:bii=2，3，…，k()为可计算的常数。

［1］Smaradache F．Only Problems，Not Solutions［M］．Chicago:Xiquan Publishing House，2001．

［2］张文鹏．关于 F．Smarandache函数的两个问题［J］．西北大学学报(自然科学版)，2008，38(2):173－176．

［3］CHEN Jianbin．Value distribution of the F．Smarandache LCM function［J］．Scientia Magna，2007(2):15－18．

［4］LE Maohua．Two function equations［J］．Smarandache Notions Journal，2004，14(6):180－182．

［5］Gorski D．The pseudo－Smarandache functions［J］．Smarandache Notions Journal，2010，13(1－2－3):140－149．

［6］Sandor J．On additive anaiogues of certain arithmeticfunction［J］．Smarandache Notions Journa，2014，14(1):128－132．

［7］Liu Hongyan，Zhang Wenpeng．A number theoretic function and its mean value property［J］．Smarandache Notions Journal，2014，13(1－2－3):155－159．

［8］赵娜娜，陈斌．关于Smarandache LCM 函数对偶函数方程的可解性［J］．渭南师范学院学报，2013，28(9):14－18．

［9］张文鹏．初等数论［M］．西安:陕西师范大学出版社，2008．

［10］Liu Hongyan，Zhang Wenpeng．On the divisor products and proper divisor products sequences［J］．Smarandache Notions Journal，2002，13(1－2－3):128－133．

［11］Lv Zhongtian．On the F．Smaradanche LCM function and its mean value［J］．Scientia Magna，2007(1):22－25．

［12］闵嗣鹤，严士健．初等数论［M］．北京:高等教育出版社，2003．