基于疲劳和13°冲击性能的组装式车轮优化设计

王登峰，张 帅，汪 勇，陈 辉

(吉林大学 汽车仿真与控制国家重点实验室，长春 130022)

0 引 言

车轮是汽车行驶系中最主要的承载件，其综合性能是衡量汽车性能的重要指标之一；同时，作为非簧载质量，其轻量化程度对汽车性能有重要影响[1]。

在车轮疲劳试验性能的仿真分析上，Shang等[2]对钢制车轮冲压过程进行了仿真分析和试验验证，研究了残余应力对车轮弯曲疲劳寿命的影响；Ballo等[3]通过材料拉伸试验得到A356-T6铝合金车轮的S-N曲线，仿真分析了车轮的弯曲疲劳寿命和应变并得到了试验验证；Oery等[4]研究了轮胎参数在径向疲劳试验仿真分析中的作用，结果表明轮胎竖直刚度对径向疲劳预测有重要影响。

从Bendsøe 等[5]提出拓扑优化的均匀化方法以来，拓扑优化的方法在结构优化设计中得到了深入发展和应用[6-9]。Zhang等[10]对铝合金车轮进行了拓扑优化，并仿真分析了优化后车轮的强度和刚度。Hu等[11]以轮辋和轮缘厚度为设计变量、弯曲疲劳和径向疲劳工况的车轮最大应力为约束并以车轮质量最小为目标，对铝合金车轮进行了优化。Xiao等[12]基于弯曲疲劳试验对钢制车轮进行了多目标拓扑优化，以柔度和模态频率为目标对车轮进行轻量化设计，并进行了应力分析和试验验证。

国内外学者在车轮13°冲击性能的仿真分析上取得了不少成果。臧孟炎等[13]对铝合金车轮13°冲击过程进行仿真分析，比较了仿真和试验的车轮应变，确认了有限元模拟的有效性。尹冀等[14]基于不同应变率下的轮毂材料本构模型对车轮13°冲击试验进行了有限元模拟，结合试验验证了仿真模型的有效性。Chang等[15]对车轮13°冲击试验进行了有限元仿真，分析了车轮的应变能密度，通过试验对比得出总塑性功可以预测车轮的失效。郑玉卿等[16]用Abaqus分析了铸铝车轮的13°冲击，以等效塑性应变作为损伤指标判定车轮是否满足动态冲击测试标准。Vinothkumar等[17]使用Abaqus对车轮13°冲击进行了仿真分析，通过与试验测得的主应变对比，验证了有限元分析的正确性。闫胜昝等[18]通过仿真分析研究了充气压力对铝合金车轮冲击试验和径向载荷试验车轮应力值的影响。Tsai等[19]通过ANSYS分析了铝合金车轮的13°冲击试验，在车轮没有装配轮胎的情况下，仿真研究了轮胎吸能0%、20%和40%三种工况下铝合金车轮的应变。张响[20]模拟了铝合金车轮的低压铸造，进行了疲劳寿命和冲击试验的简化仿真分析，实现了工艺过程模拟与结构有限元模拟的仿真技术集成。Chauhan等[21]对车轮13°和90°冲击进行了仿真分析，并通过试验验证了车轮等效塑性应变和应变能密度对车轮失效预测的有效性。此外，国内外学者在车轮新材料的应用和轮胎对冲击试验仿真的影响方面也进行了研究[22-25]。

综上可知，以上研究多集中在疲劳和冲击试验的仿真分析和试验验证上，或者是研究车轮应变和应变能密度对车轮失效的预测；在优化设计中将冲击性能仅用作检验校核优化后的车轮，而不是直接作为约束条件；车轮轻量化设计时没有对车轮进行参数化，而是在参数化阶段设置多组模型进行对比或者仅将车轮厚度作为设计变量，极大减弱了车轮结构的变形能力，优化空间和效果有限。同时，以上研究仅涉及概念设计阶段基于疲劳试验的拓扑优化，没有研究参数化阶段的多目标优化；没有综合研究疲劳性能和冲击性能与车轮结构的关系；所研究的车轮均为单一材料的整体式结构，没有研究异种材料连接的组装式车轮。

1 动态疲劳试验参数设置

根据《乘用车车轮性能要求和试验方法》(GB/T 5334-2005)，车轮应满足动态弯曲疲劳试验和动态径向疲劳试验要求。

1.1 动态弯曲疲劳试验参数

车轮动态弯曲疲劳试验方法如图1所示。试验时在加载轴末端施加力F产生弯矩，车轮在恒定的弯矩作用下旋转，达到10万次循环前车轮不能出现新可见裂纹、加载点位移偏移量不能超过初始全加载位移偏移量的20%。

取加载轴长度L=1 m。试验弯矩M(N·m)和加载力F(N)满足下式：

M=(μR+d)FvS

(1)

(2)

式中：μ为轮胎与路面间的摩擦因数；R为轮胎静负荷半径(m)；d为车轮偏距(m)；Fv为车轮最大垂直静负荷(N)；S为强化试验系数。

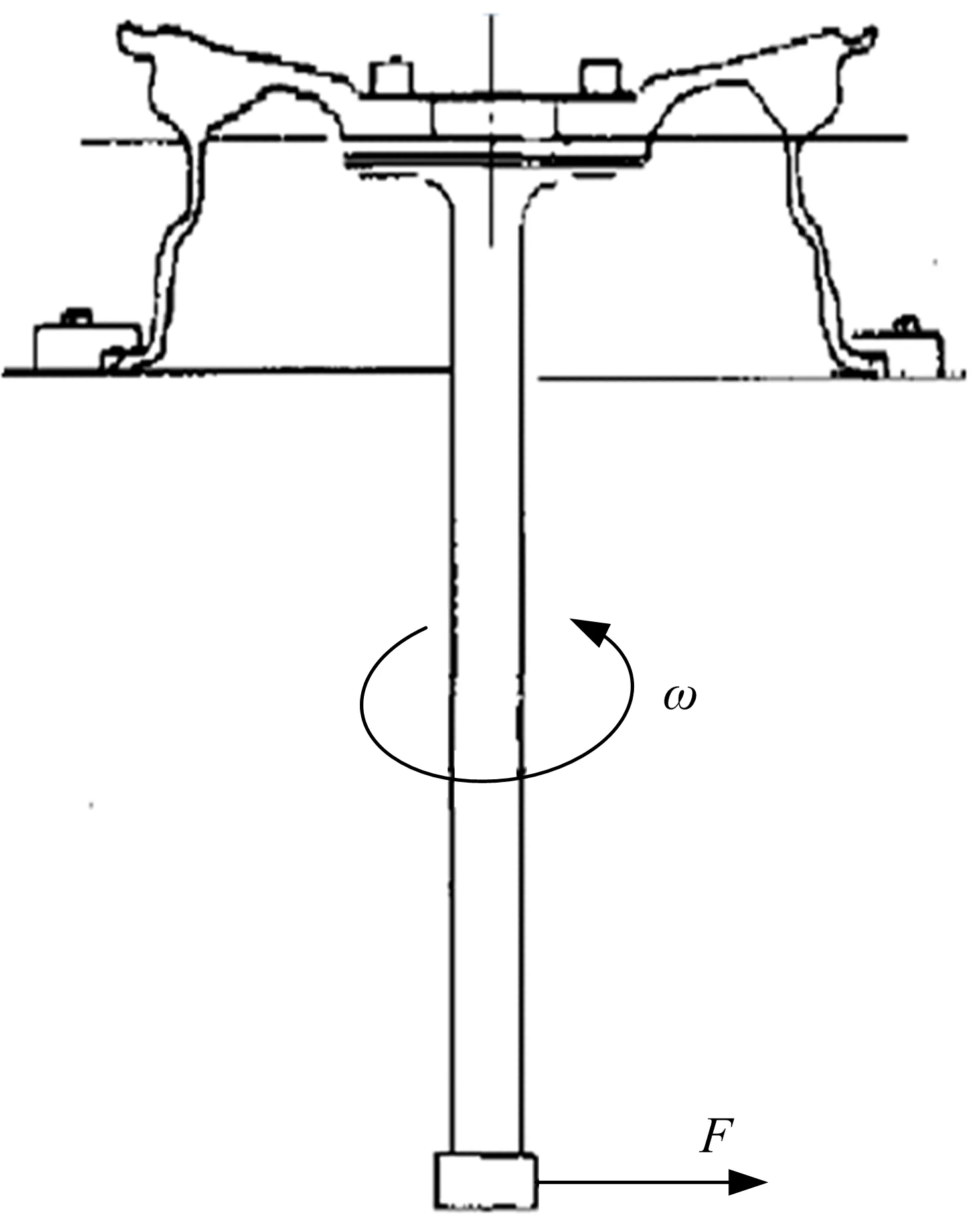
图1 车轮动态弯曲疲劳试验示意图Fig.1 Schematic diagram of wheel dynamicbending fatigue test

结合车轮型号，试验参数确定如下：μ=0.7，R=0.316 m，d=0.053 m，Fv=6027 N，S=1.6。由式(1)和式(2)可知：M=2644 N·m，F=2644 N。

1.2 动态径向疲劳试验参数

车轮动态径向疲劳试验方法如图2所示。车轮在试验台上转动时，转鼓向其传递径向负荷Fr，在循环50万次前车轮不能出现新可见裂纹。

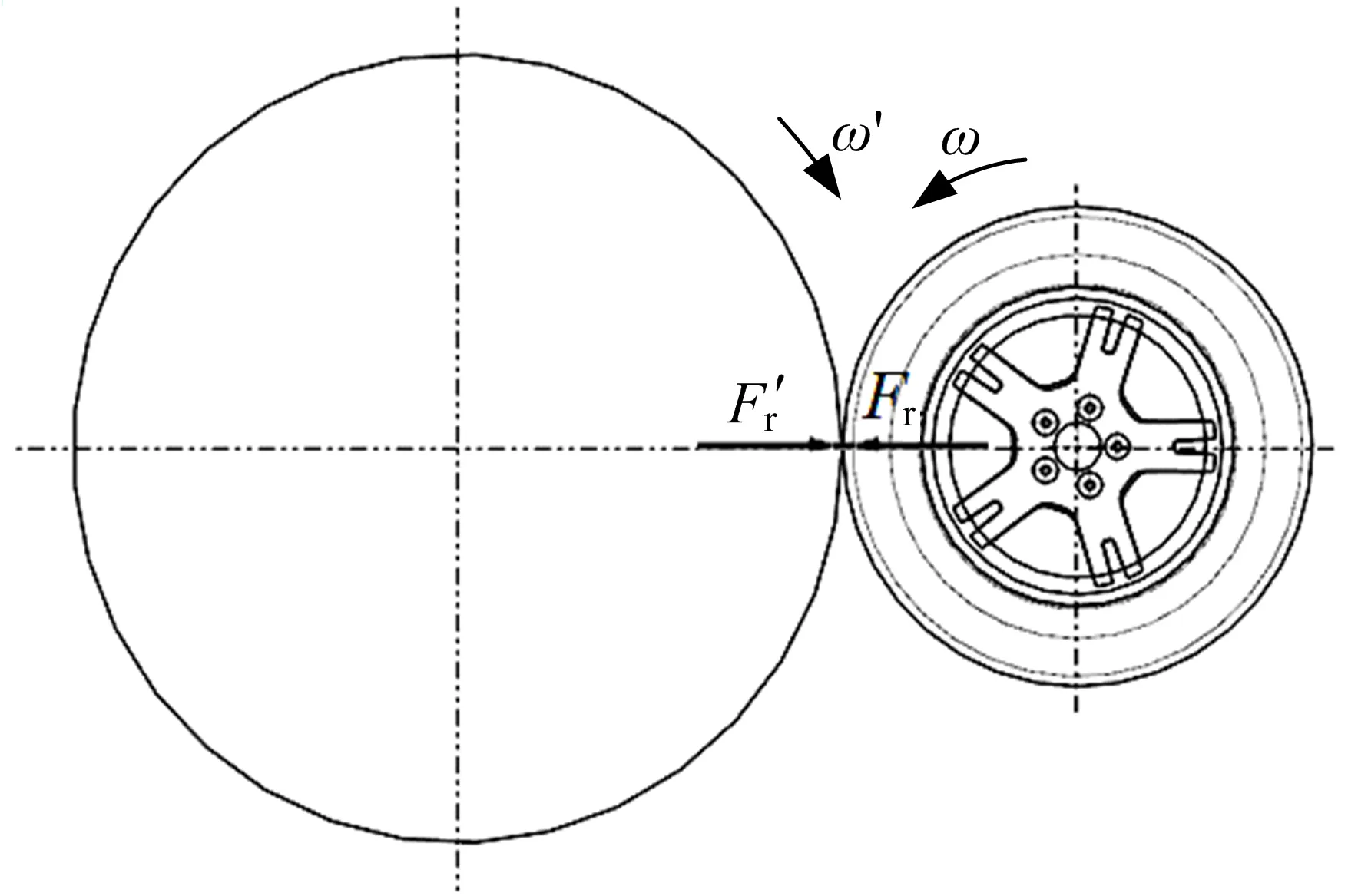
图2 车轮动态径向疲劳试验示意图Fig.2 Schematic diagram of wheel dynamic radial fatigue test

车轮的径向负荷Fr(N)，满足下式：

Fr=FvK

(3)

式中：Fv为车轮最大垂直静负荷(N)；K为强化试验系数。

结合车轮型号，试验参数确定如下：Fv=6027 N，K=2.25。根据式(3)，则Fr=13561 N。车轮充气压力选为0.45 MPa。

车轮的径向负荷通过轮胎对称加载在轮辋两侧的胎圈座上，并在2θ0角度内成余弦分布，如图3所示。

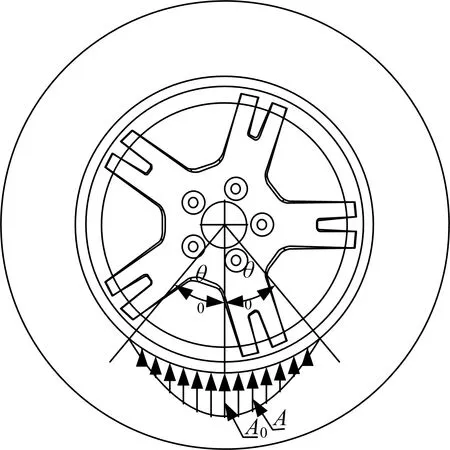
图3 车轮径向加载示意图Fig.3 Schematic diagram of wheel radial loading

在图3中设立柱坐标系，设单侧胎圈座受力为F，加载处半径为rb(mm)，加载面的宽度为b(mm)，单个加载压力为A(MPa)、与竖直方向夹角为θ(rad)，则加载压力的余弦振幅A0(MPa)推导如下：

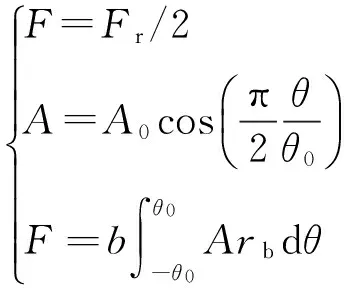
(4)

(5)

根据Stearns等[26]研究，θ0取2π/9时最能模拟载荷的真实情况。结合车轮型号，rb=202.8 mm，b=20 mm。根据式(5)，A0=1.88 MPa。

2 组装式车轮设计

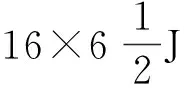
图4 车轮概念设计模型Fig.4 Concept design model of wheel

2.1 车轮联合拓扑优化建模

在车轮概念设计模型中装配1 m长的加载轴，将该模型导入HyperMesh中进行几何清理，并采用四面体单元进行网格划分。其中，轮辋单元大小为4 mm、轮辐拓扑空间单元大小为5 mm、加载轴单元大小为10 mm，允许最小尺寸均为2 mm。共离散为417049个单元，94754个节点。

设置动态弯曲疲劳试验和动态径向疲劳试验两个工况，进行车轮联合拓扑优化。动态弯曲疲劳试验工况下，加载轴和车轮安装面之间的螺栓连接用RBE2模拟，约束轮辋内侧外沿节点的全部自由度，在加载轴末端施加2644 N的力。动态径向疲劳试验工况下，约束车轮安装面上5个螺栓孔的全部自由度，胎圈座2θ0内加载振幅为1.88 MPa的余弦压力，两胎圈座之间的轮辋外表面上加载0.45 MPa的充气压力。车轮联合拓扑优化的有限元模型，如图5所示。

图5 车轮联合拓扑优化有限元模型Fig.5 Finite element model for united topologyoptimization of wheel

轮辋、轮辐和加载轴分别赋予镁合金AZ91D，铝合金6061和A3钢的材料属性。各材料参数如表1所示。

表1 材料参数Table 1 Material parameters

有限元分析时，使用材料的许用应力作为应力约束来保障车轮的强度，镁、铝合金的安全系数s取1.2来计算许用应力，材料属性见表2。

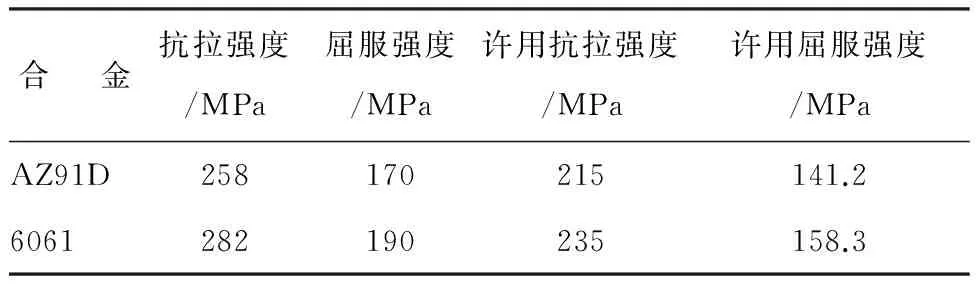
表2 镁、铝合金材料属性Table 2 Materialproperties of magnesium alloyand aluminum alloy

2.2 车轮联合拓扑优化

在优化设计中，把刚度增大问题等效为柔度减小问题来研究，柔度则用应变能来定义[29,30]。多个工况的柔度加权和即为加权柔度，如下式所示:

(6)

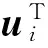
在Optistruct中进行联合拓扑优化。为了模拟动态疲劳试验时载荷的周向动态变化，添加周向对称约束[31]。为了模拟车轮的锻压工艺，添加拔模约束。为了清晰观测拓扑优化结果中的材料分布，添加最小密度单元约束，约束单元最小尺寸为2 mm。约束车轮的强度和刚度，车轮强度用许用屈服应力约束，动态弯曲疲劳试验工况的车轮刚度通过车轮节点的最大偏移量约束，动态径向疲劳试验工况的车轮刚度通过车轮的加权柔度约束。以车轮单元密度为设计变量，最大von Mises应力、节点最大偏移量为约束条件，质量最小为目标函数进行联合拓扑优化。拓扑优化的数学模型为：

式中：m(ρ)为车轮质量(t)；σb(ρ)和σr(ρ)分别为动态弯曲疲劳试验和动态径向疲劳试验工况下轮辐的最大von Mises应力(MPa)；σd为轮辐许用屈服应力(MPa)，σd=158.3 MPa；D(ρ)为动态弯曲疲劳试验工况下车轮节点的最大偏移量(mm)；D0为车轮节点许用偏移量(mm)，D0=0.8 mm；Cr(ρ)为动态径向疲劳试验工况下车轮的加权柔度(N·mm)；Cr0为车轮柔度许用值(N·mm)，Cr0=3800 N·mm；ρ为单元密度。

2.3 车轮联合拓扑优化结果

设置车轮的单元密度为0.3时，车轮联合拓扑结果如图6所示。

图6 车轮联合拓扑优化结果Fig.6 United topology optimization results of wheel

如图6所示，拓扑优化结果中车轮的材料分布由内部的应力传递路径决定，材料密度与应力值有关。动态弯曲疲劳试验时，弯矩沿着车轮安装面螺栓孔从轮辐传递到轮辋并依次递减。动态径向疲劳试验时，两胎圈座之间的轮辋表面受均匀气压，胎圈座承受了在2θ0角度内成余弦分布的径向负荷，应力沿着轮辋向轮辐扩散。所以联合拓扑优化时，轮辐根部形状受动态弯曲疲劳试验工况影响大；轮辋和轮辐交接处受动态径向疲劳试验工况影响大，该处材料密度分布均匀，在设计组装式车轮时可以设计成圆环。

2.4 组装式车轮建模

在HyperView中，将联合拓扑优化的车轮结构导出三维几何模型。参照该模型尺寸，在UG中建立拓扑优化后的组装式车轮模型，如图7所示。

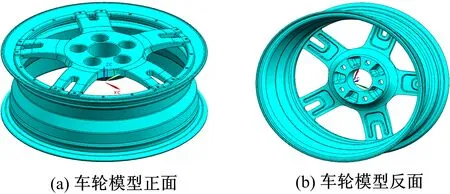
图7 组装式车轮模型Fig. 7 Assembled wheel model

3 车轮13°冲击性能分析

3.1 试验工况

根据《道路车辆轻合金车轮冲击试验方法》(GB/T 15704-2012)，车轮应满足13°冲击试验要求，试验方法如图8所示。将试验车轮和轮胎总成安装到试验机上，车轮的轴线应与铅直方向成(13±1)°角；冲锤在轮缘最高点上方(230±2)mm处，并与轮缘重叠(25±1)mm；然后释放重锤，进行冲击。冲击结束后不能有可见裂纹穿透车轮中心部分的截面，车轮中心部分与轮辋不能分离，1 min内轮胎气压不能全部泄露。

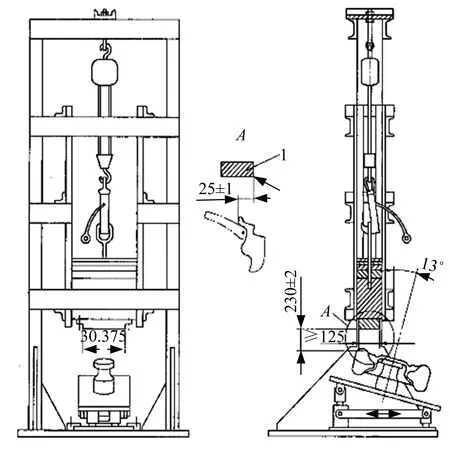
图8 车轮13°冲击试验示意图Fig.8 Schematic diagram of 13 ° impact test of wheel

冲锤质量满足下式：

m=0.6W+180

(8)

式中：m为冲锤质量(kg)；W为车轮最大静载荷(kg)。

结合车轮型号，试验参数确定如下：W=615 kg，轮胎充气压力为0.245 MPa。根据式(8)，则m=549 kg。

3.2 控制方程

车轮冲击的有限元仿真分析，属于材料非线性、几何非线性和接触非线性的问题，采用拉格朗日法描述物体的运动和变形，每个节点和整体都满足质量、动量和能量守恒。在笛卡尔坐标系Ox1x2x3中，质量守恒方程、动量守恒方程和能量守恒方程如式(9)所示：

(9)

式中：ρ0(a)为初始时刻，点ai(i=1,2,3)处的物质密度；ρ(x)为经历时间t后，点xj(a1,a2,a3,t)(j=1,2,3)处的物质密度，也记为ρ；vi为点xi处的速度；Xi为单位体积的体力；σij为应力场；u为单位质量内能；hi为热通量矢量h的分量；Vij为应变率张量。

其中，物体在运动和变形过程中的应力边界条件、位移边界条件和接触边界条件如下式所示：

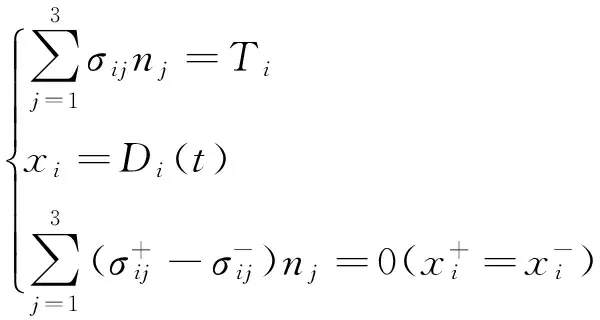
(10)

式中：σij为应力场；nj(j=1,2,3)为边界面的外法线方向余弦；Ti(i=1,2,3)为面力载荷；xi为位置坐标；Di(t)为位移函数。

通过将以上边界条件代入各节点进行运算可以得到每一个节点的运动规律和能量变化规律，即整个结构碰撞响应的特征关系。

本文采用LS-DYNA进行冲击仿真，用罚函数法处理接触问题，分别对单个部件和整体采用局部和整体沙漏控制。采用显式中心差分算法，其稳定性决定于时间步长，积分时间步长满足下式：

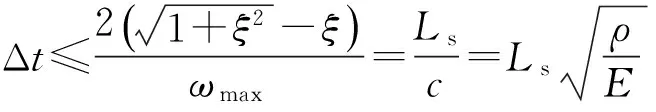
(11)

式中：ξ为系统阻尼比；ωmax为系统最大固有频率；Ls为单元特征长度；c为物质中的声速；ρ为物质密度；E为物质弹性模量。

3.3 材料模型

镁、铝合金在冲击过程中受应变硬化和应变率硬化的影响较大，因此，需要设置考虑应变率效应的镁、铝合金材料模型。

AZ91D镁合金和6061铝合金试件按照GB/T 2975-1998进行取样，并按照GB/T 228-2002进行静态拉伸试验，分别在0.003、0.01、0.1、1、10、25、100和1000 s-1应变率下测量AZ91D和6061的应力应变数据，结果如图9所示。

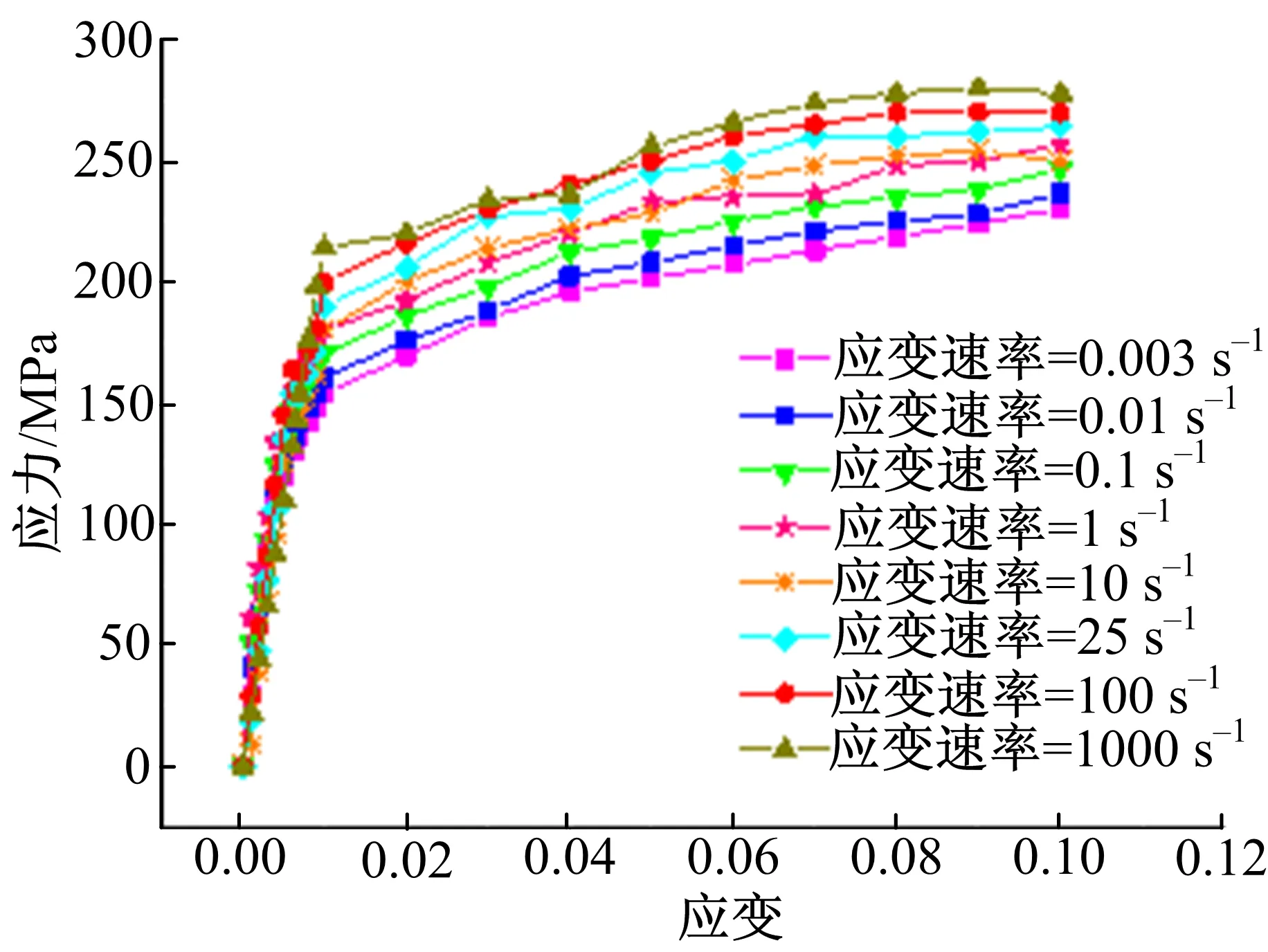
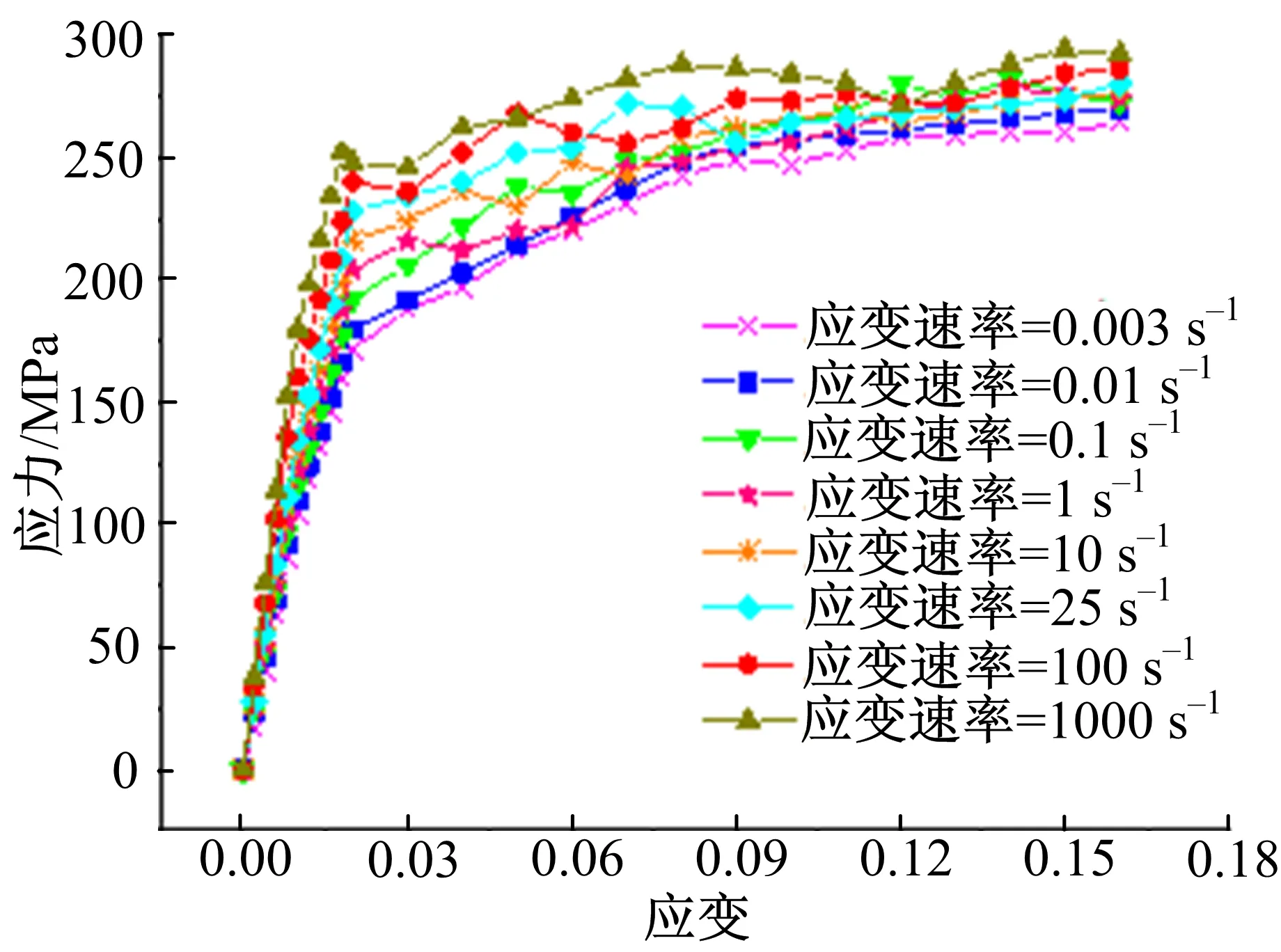
图9 车轮材料应力-应变实验曲线Fig.9 Stress-strain experimental curves of wheel materials

轮胎分为胎面、两胎侧、胎体(Carcass)和内衬层(Inner liner)5个部分建模，胎体采用各向同性弹性材料，使用MAT1材料模型；胎面、两胎侧和内衬层采用各向同性超弹性材料，使用Yeoh材料模型。

Yeoh模型适合模拟炭黑填料天然橡胶的大变形行为，并且可以用简单的单向拉伸试验的数据去模拟其他变形的力学行为。Yeoh形式可以产生典型的S形的橡胶应力-应变曲线，其表达式如下：

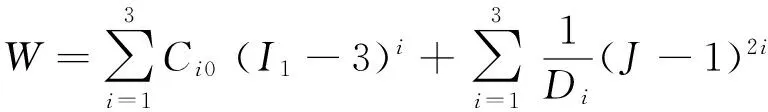
(12)

式中：Ci0和Di均为待定材料模型参数；J为弹性体积比；I1为第一阶应变不变量。

对于不可压缩材料，Yeoh形式简化为下式：

(13)

在小变形情况下，C10代表初始剪切模量；由于第2个系数C20为负，在中等变形时可反映材料的软化现象；但由于第3个系数C30为正，在大变形情况下又可描述材料的硬化现象。

依据文献[32]，胎面、两胎侧和内衬层的橡胶材料材料参数见表3。胎体的材料参数如下：密度为7.80×10-9t/mm3；弹性模量为2.07×5 MPa；泊松比为0.3。

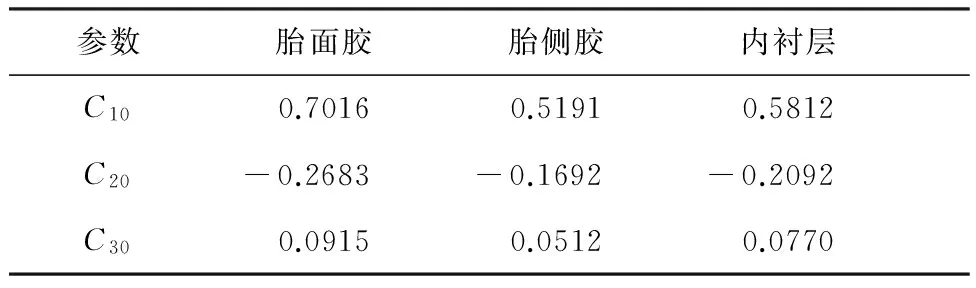
表3 各橡胶材料的Yeoh模型参数Table 3 Parameters of Yeoh model for rubber materials

3.4 边界条件

在Hypermesh中建立车轮13°冲击试验台架的有限元模型，如图10所示。

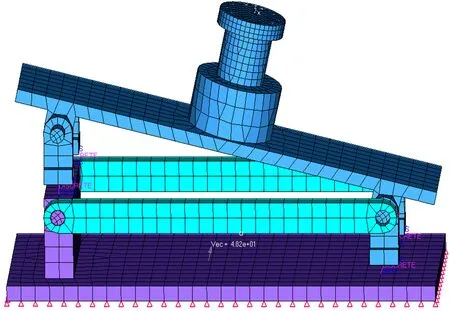
图10 车轮13°冲击试验台架有限元模型Fig.10 Finite element model of test bench in 13° impact of wheel

图10中，台架上、下支架用4个天然橡胶垫固连，并通过转动臂连接。为了避免出现较大的沙漏和质量增加、甚至负体积或节点速度过高等错误，每个橡胶垫分别用一个弹簧单元来模拟橡胶的静态变形特征和一个阻尼单元来模拟橡胶的动态阻尼特性。弹簧单元采用SDMAT1材料模型，k=326 N/mm；阻尼单元采用SDMAT2材料模型，c=500 N·s/mm。上、下支架和转动臂的销孔之间的转动使用Revolute joint功能来实现。

在Hypermesh中建立车轮13°冲击试验的有限元模型，设置冲锤正对辐条和正对窗口两种工况，如图11所示。

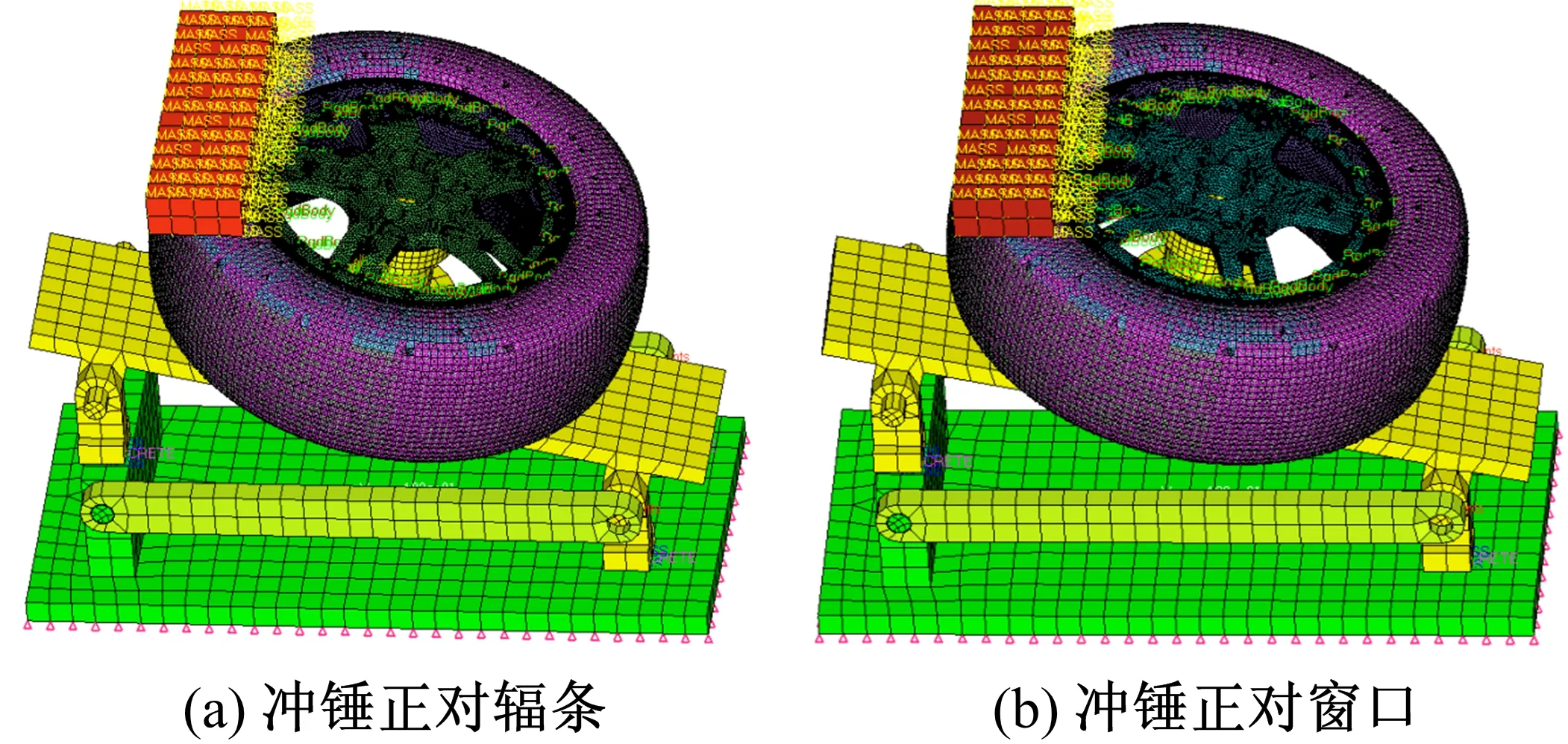
图11 车轮13°冲击试验有限元模型Fig.11 Finite element models of 13° impact test of wheel

轮辋和轮辐分别离散为边长为4 mm和5 mm的四面体单元，轮胎、试验台架和冲锤分别离散为边长为10 mm、30 mm和30 mm的四边形和三角形混合壳单元。轮辋和轮辐之间的螺栓连接用RBE2模拟。共离散为519 762个单元，118 515个节点。

AZ91D镁合金轮辋、6061铝合金轮辐和A3钢试验台架采用各向同性弹塑性材料，使用MAT24材料模型。A3钢冲锤采用刚体材料，使用MAT20材料模型。

在轮胎和轮辋安装贴合部位的接触面间定义*Contact_shell_edge_to_surface_offset来模拟预紧力，该定义采用罚函数算法、约束平动与转动、考虑失效。轮胎和轮辋中间定义*Airbag_simple_pressure_volume气囊，初始气压为0.245 MPa。

为了节省计算时间，设置冲击初始时刻冲锤在轮缘最高点上方2 mm处，则初始速度v=-2124 mm/s。冲锤配重0.549 t。整个模型都施加重力场，g=9800 mm/s2。约束下支架底板的所有自由度和冲锤的转动自由度。根据式(11)，时间步长设为10-6s。模型计算结束时间设为0.05 s。

3.5 性能分析

将两个工况下的有限元模型分别导入LS-DYNA进行计算，仿真计算后，质量增加了0.23%、能量变化了0.07%，均低于5%的要求。这证明了有限元模型的仿真结果是可信的。仿真计算中两个有限元模型的能量变化曲线如图12所示。

由图12可知，沙漏能几乎为零，总能量保持不变。随着时间的增加，动能减小、内能增大，在45 ms时冲击结束，之后各能量保持不变。

在两种工况下，冲击开始时轮胎内的气压有所降低，冲击结束时趋于稳定，如图13所示。

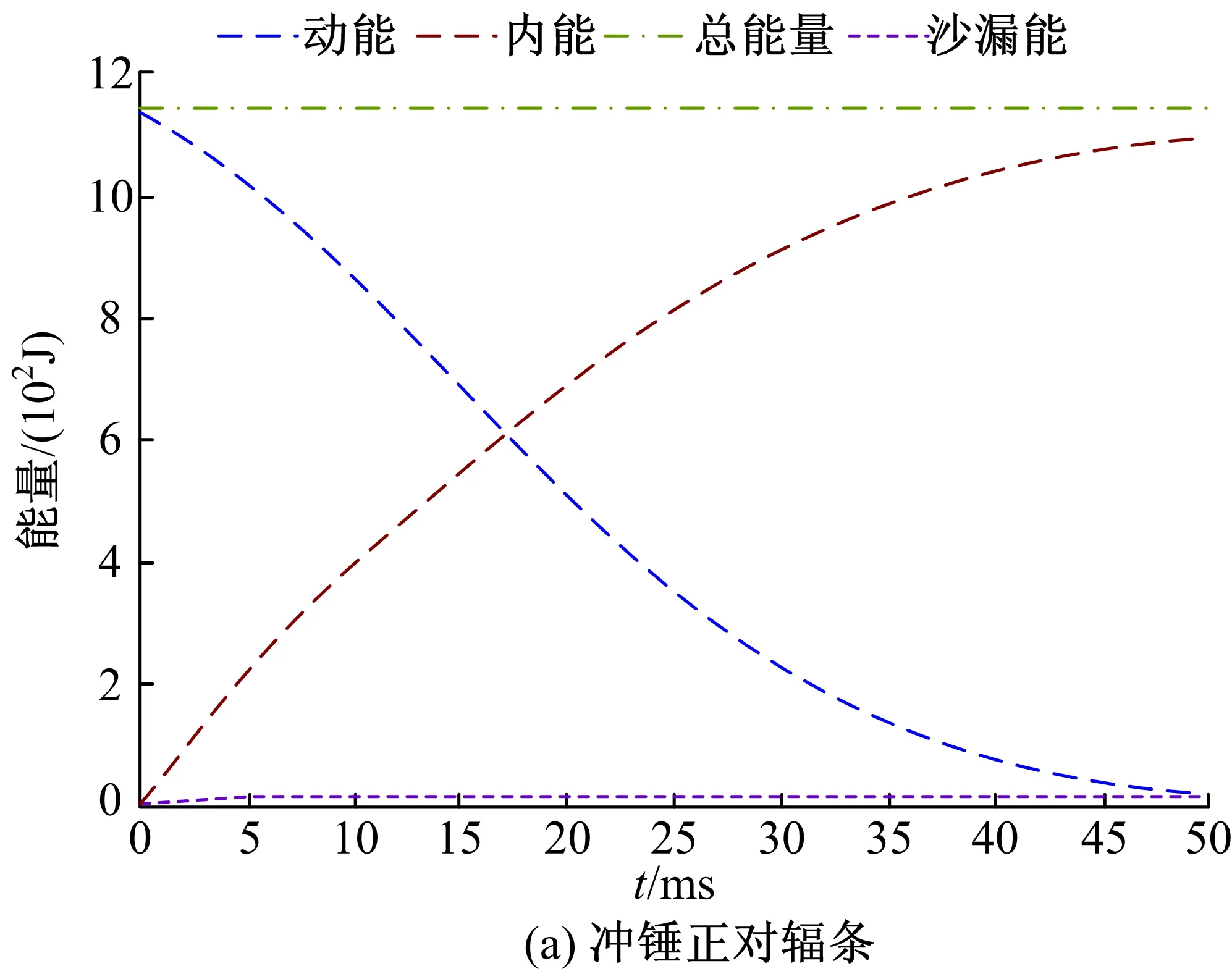
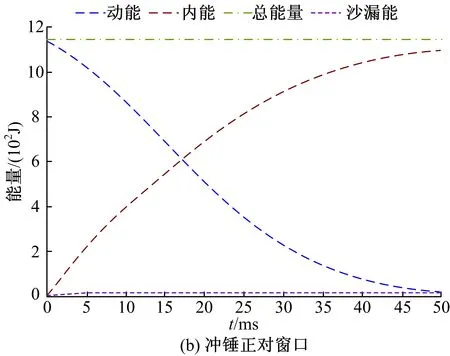
图12 仿真分析中的能量变化曲线Fig. 12 Energy variation curves in simulation analysis

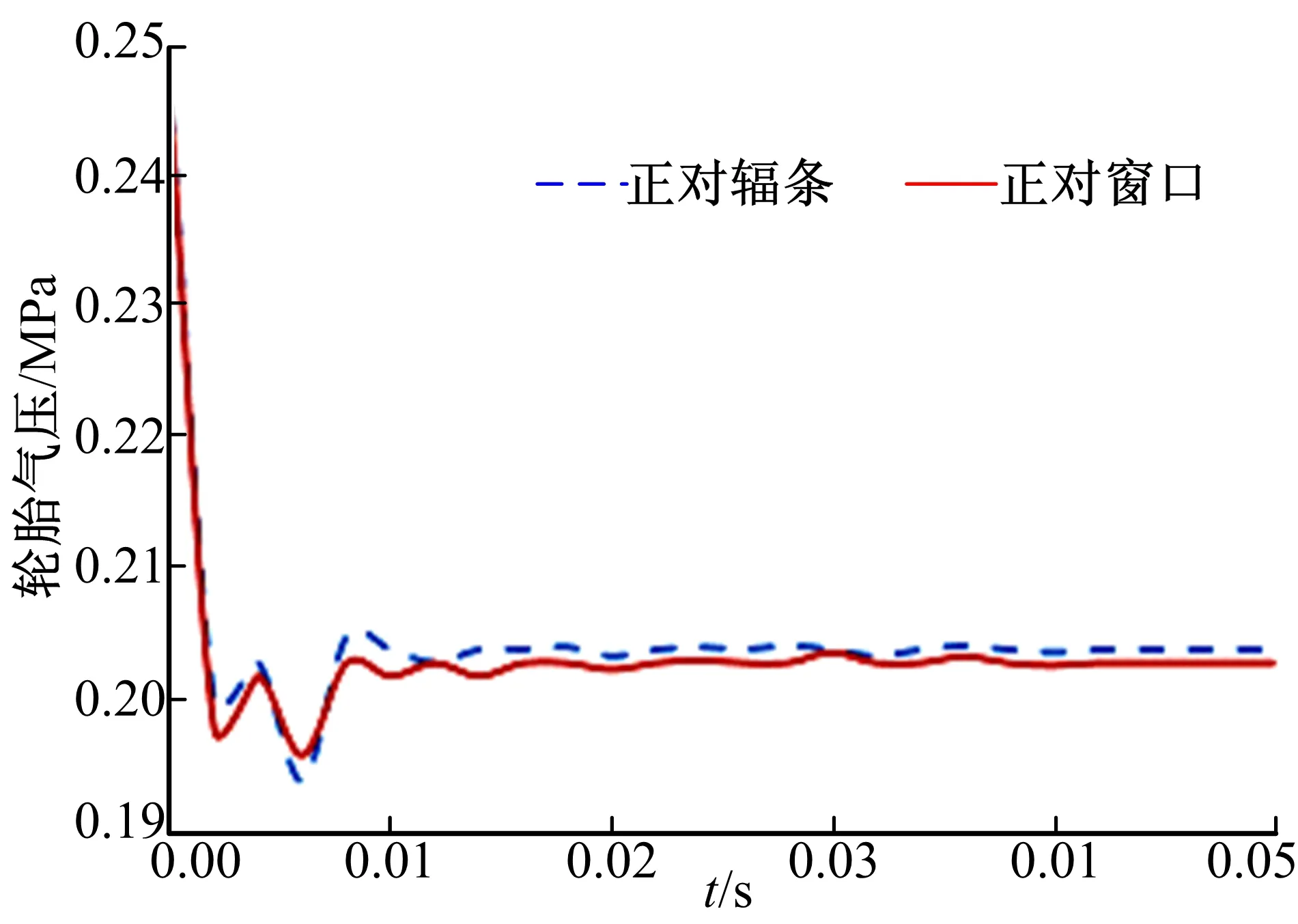
图13 车轮13°冲击中轮胎气压曲线Fig.13 Tirepressure curves in 13° impact test of wheel

车轮的最大应变发生在轮辐根部上表面，轮辋的应变很小。车轮在两种工况下的应变云图如图14所示。

由图14可知，冲锤正对辐条冲击时，该辐条根部上表面的应变最大，为7.20%；冲锤正对窗口冲击时，该窗口两侧辐条根部的应变最大，为6.53%。冲锤正对辐条冲击时，车轮的受力变形更大、损伤更严重。所以，后文的多目标优化中，将以冲锤正对辐条冲击时轮辐的应变为目标、冲锤正对窗口冲击时轮辐的应变为约束。但是轮辐的应变小于8.7%，轮辋的应变远小于8.1%，均不会产生裂纹；轮辐与轮辋连接处的应变也很小，不会发生轮辐与轮辋分离。车轮模型满足13°冲击试验要求，并有进一步的优化空间。

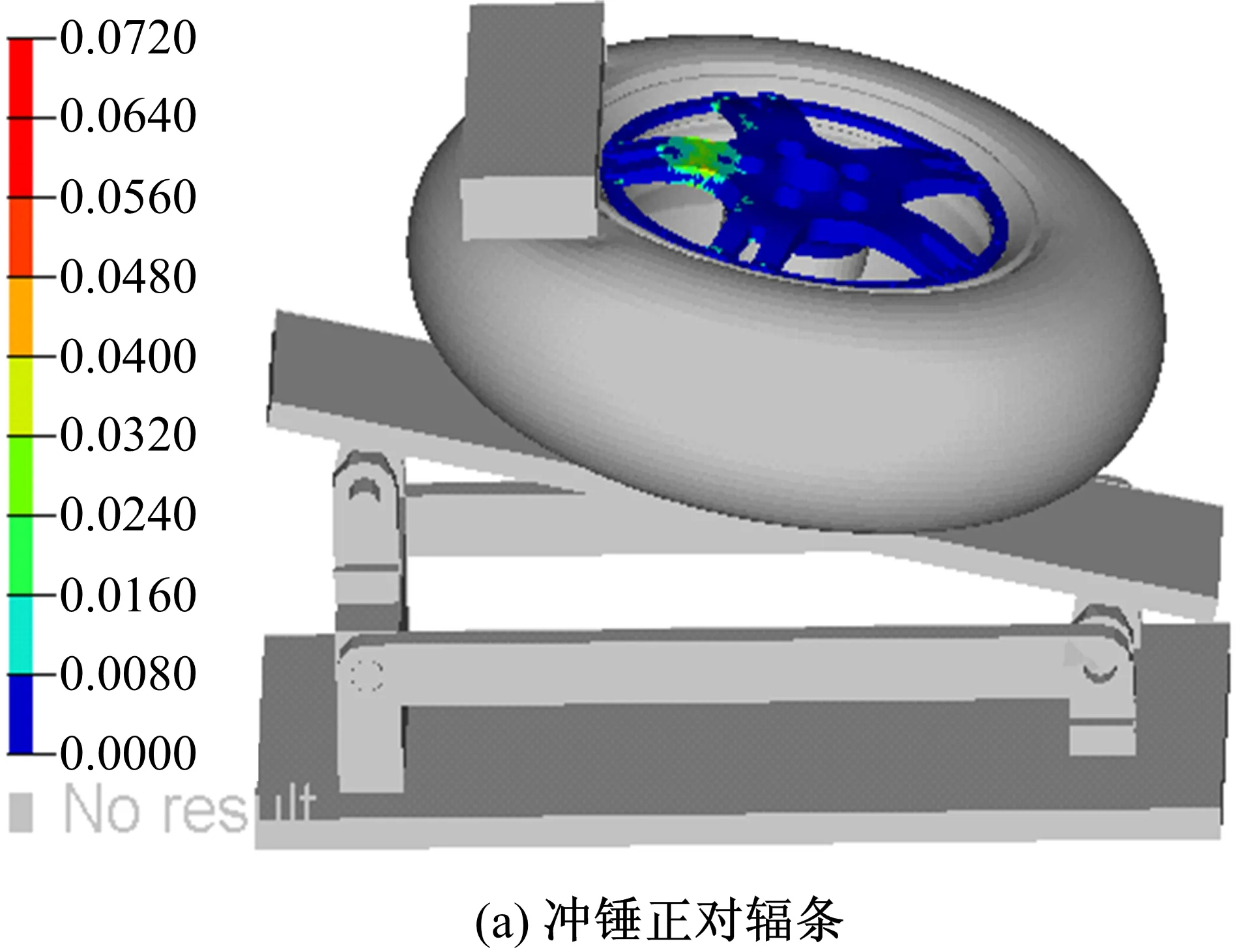
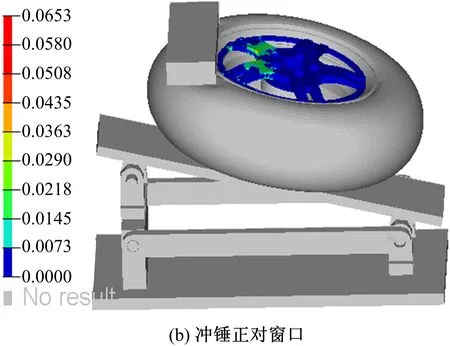
图14 车轮应变云图Fig.14 Straincountours of wheel

6061铝合金轮辐弹性变形极限的应变为0.28%，13°冲击后应变超过0.28%的轮辐单元，如图15所示。

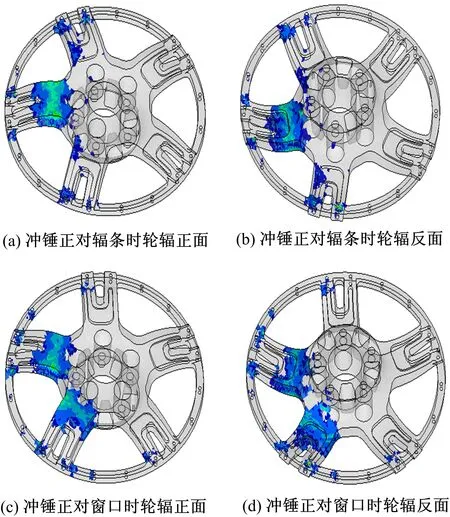
图15 应变大于0.28%的轮辐单元Fig.15 Disc elements of strain larger than 0.28%

由图15可知，大于弹性极限应变的单元多集中在轮辐根部。轮辐根部的结构尺寸对车轮13°冲击性能的影响很大，在多目标优化设计时，减小其他部位尺寸而增大轮辐根部尺寸能同时满足车轮的轻量化和13°冲击性能的提升。此外，在冲击部位的轮辐和圆环交结处、圆环螺栓孔处也聚集了大于弹性极限应变的单元。

4 组装式车轮多目标优化设计

4.1 车轮参数化建模

为了研究组装式车轮结构与13°冲击性能之间的关系，并对车轮进行多目标优化设计，需要建立参数化车轮模型[33,34]。

基于网格变形技术，采用DEP-MeshWorks软件分别对冲锤正对辐条冲击和正对窗口冲击两种工况下的车轮进行参数化，建立组装式车轮的参数化模型，定义10个厚度变量和2个形状变量(记为x1，x2，…，x12)，如图16所示。表4给出了各设计变量的取值范围。

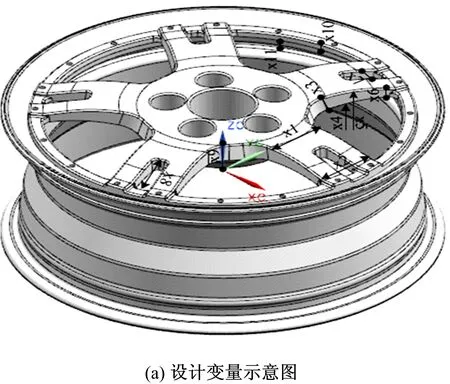
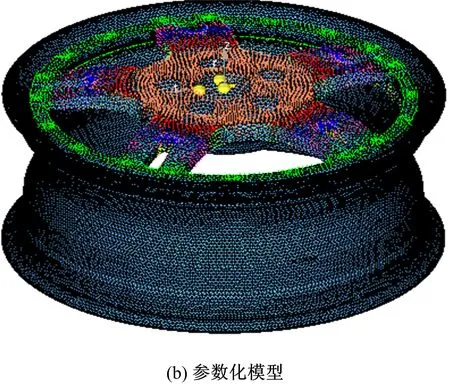
图16 车轮设计变量及参数化模型Fig.16 Design variables and parametric model of wheel表4 各设计变量及取值范围Table 4 Designvariables and range of values

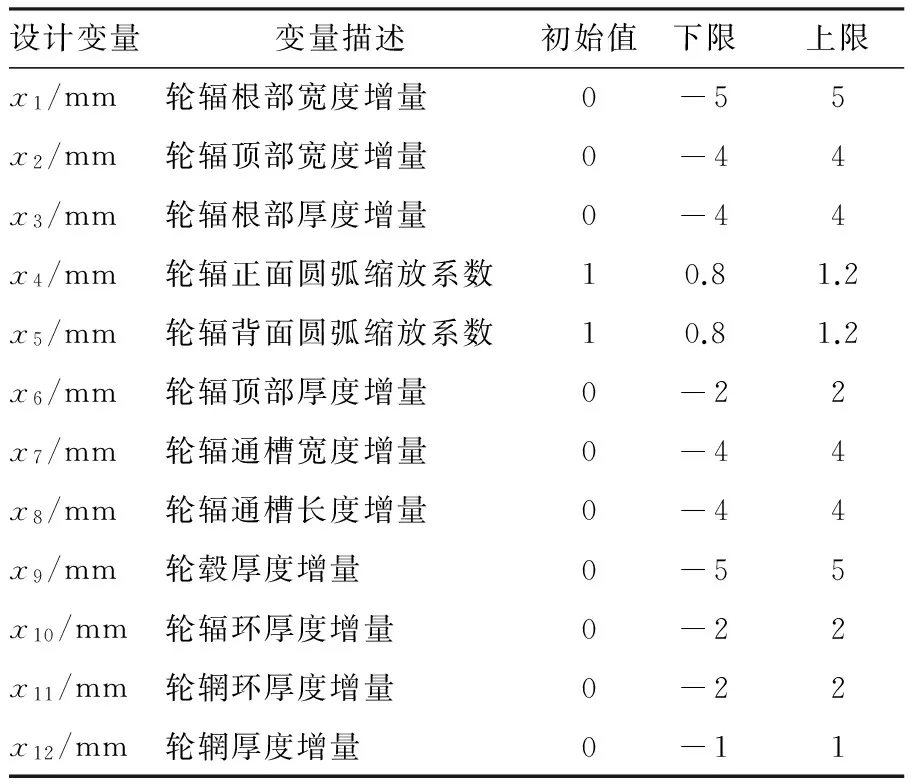
设计变量变量描述初始值下限上限x1/mm轮辐根部宽度增量0-55x2/mm轮辐顶部宽度增量0-44x3/mm轮辐根部厚度增量0-44x4/mm轮辐正面圆弧缩放系数10.81.2x5/mm轮辐背面圆弧缩放系数10.81.2x6/mm轮辐顶部厚度增量0-22x7/mm轮辐通槽宽度增量0-44x8/mm轮辐通槽长度增量0-44x9/mm轮毂厚度增量0-55x10/mm轮辐环厚度增量0-22x11/mm轮辋环厚度增量0-22x12/mm轮辋厚度增量0-11

4.2 近似模型

为了提高优化效率，使用近似模型进行多目标优化设计[35]。采用径向基RBF网络近似模型代替有限元计算来获取各设计变量和各性能指标之间的关系[36,37]。在两个有限元模型中，使用最优拉丁超立方设计方法分别采样80个试验点来拟合近似模型；另外采用Box-Behnken设计分别采样10个试验点来检验近似模型精度。通过决定系数R2检验近似模型的精度[38]，其表达式为

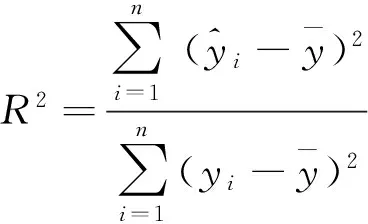
(14)

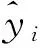
R2的值越接近1，则近似模型的拟合精度越高。各性能指标的决定系数R2值均大于92%，满足近似模型拟合精度要求。部分性能指标的近似模型精度检验结果如图17所示。

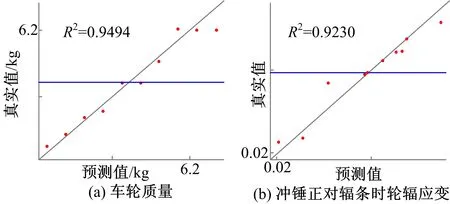
图17 部分性能指标的近似模型精度Fig.17 Surrogate model accuracy of partialperformance indexes

4.3 多目标优化设计

综合考虑车轮13°冲击的性能指标，对组装式车轮进行多目标优化设计，优化的数学模型为:

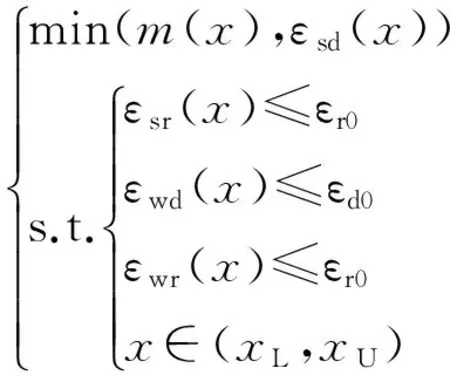
(15)

式中：m(x)为车轮质量(kg)；εsd(x)和εsr(x)分别为冲锤正对辐条冲击时轮辐和轮辋的最大应变；εwd(x)和εwr(x)分别为冲锤正对窗口冲击时轮辐和轮辋的最大应变；εd0和εr0分别为轮辐和轮辋的许用应变，εd0=8.7%，εr0=8.1%；x为设计变量，xL和xU分别为设计变量取值的下限和上限。

将13°冲击性能指标计算软件集成到多学科优化设计平台Isight软件中，建立基于径向基RBF网络近似模型和第二代非劣排序遗传算法(NSGA-Ⅱ)的组装式车轮多目标优化分析模型，如图18所示。

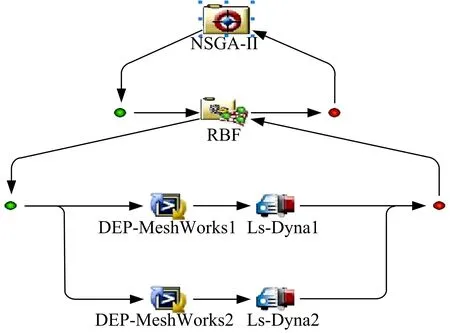
图18 车轮多目标优化分析模型Fig.18 Multi-objectiveoptimization andanalysis model of wheel

4.4 优化结果分析

经过8002次迭代，优化得到的Pareto前沿如图19所示。

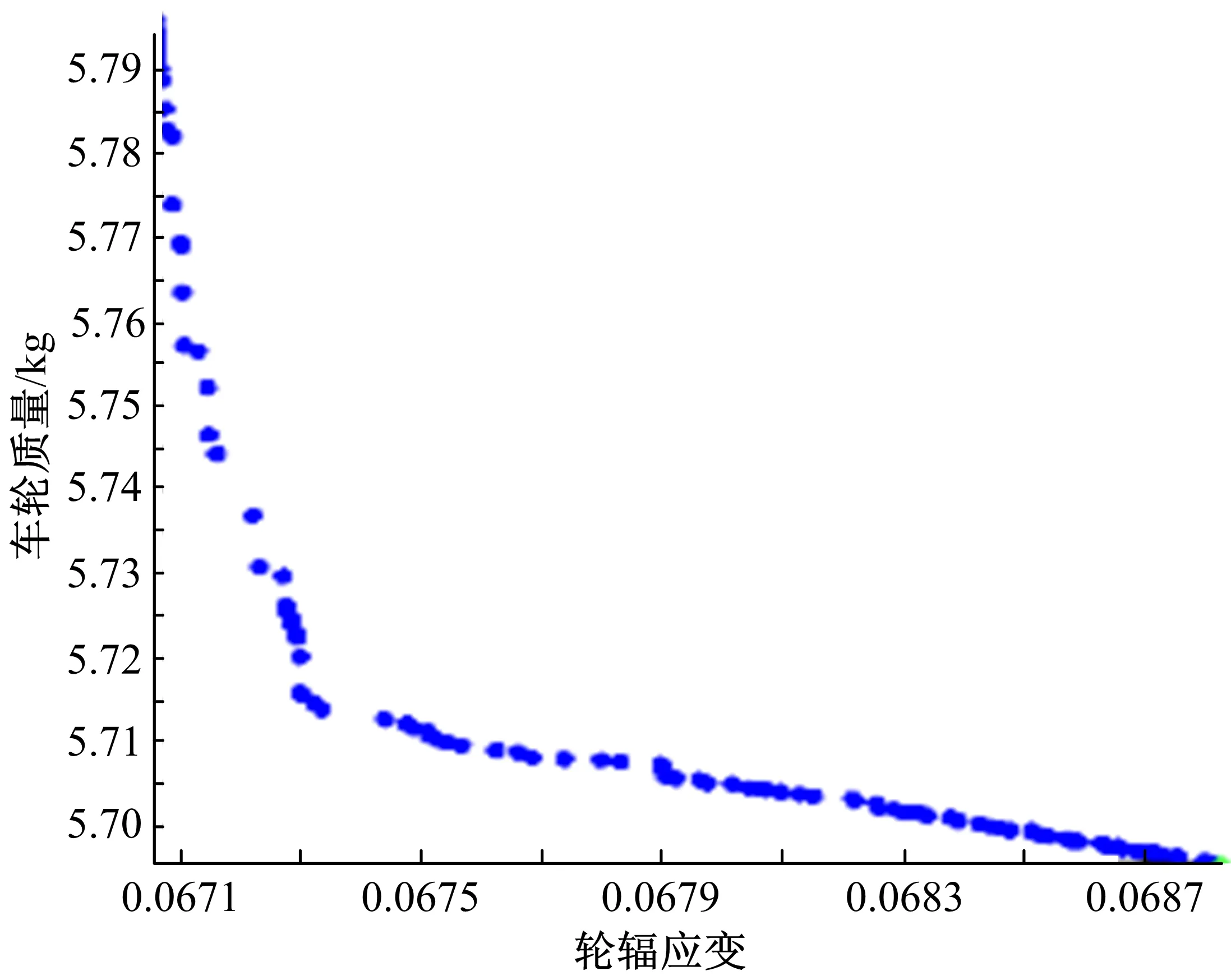
图19 Pareto前沿Fig. 19 Pareto frontier

依据图19，车轮质量和轮辐冲击应变两个目标函数是相互矛盾的，其中一个最优要以另一个最差为代价。本文优先考虑车轮的轻量化，冲击性能属于次要目标，因此要在满足车轮13°冲击性能的条件下尽量降低质量。在Pareto前沿中选取一个妥协解，如图中绿点所示。优化前后各设计变量和各性能指标的对比分别如表5和表6所示。

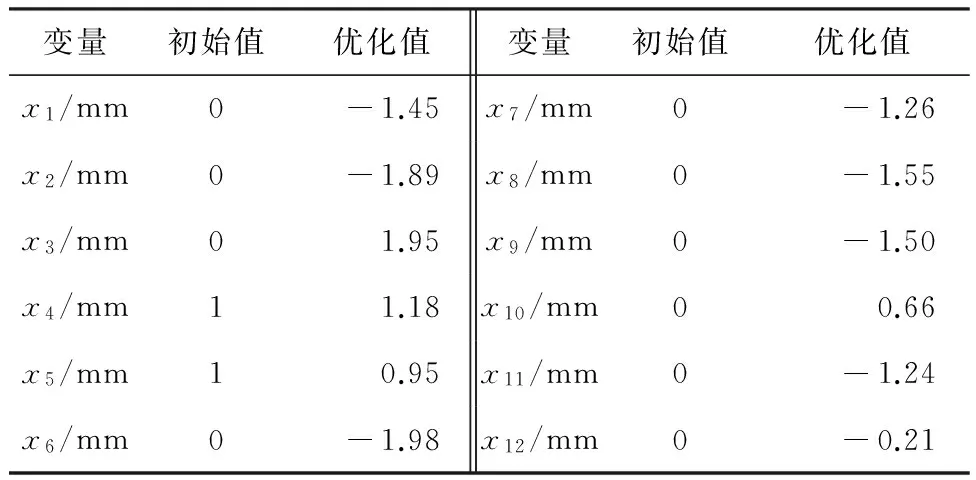
表5 优化前、后设计变量取值Table 5 Values of design variables before and afteroptimization

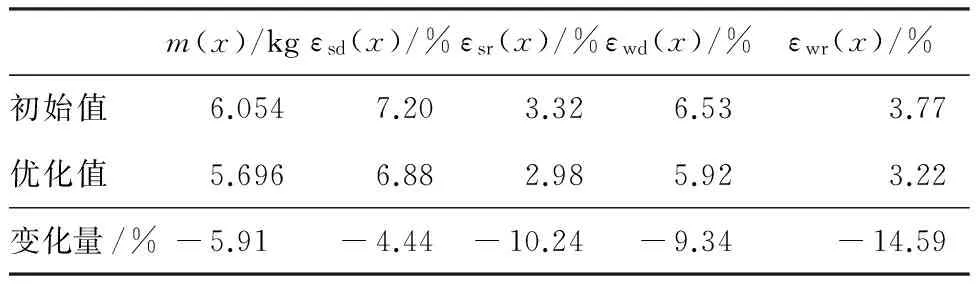
表6 优化前、后各性能值对比Table 6 Values of performance indexes before and afteroptimization

5 结 论

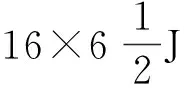
(2)建立了车轮13°冲击试验的有限元模型，并检验了模型的可信性。使用了轮胎的Yeoh材料模型，基于不同应变率下AZ91D和6061的材料本构关系分别分析了冲锤正对辐条和正对窗口冲击两种工况下车轮的应变，其中冲锤正对辐条冲击时车轮应变更大。

(3)大于轮辐弹性极限应变的单元多集中在轮辐根部。轮辐根部的结构尺寸对车轮13°冲击性能的影响很大，减小其他部位尺寸而增大轮辐根部尺寸能同时满足车轮的轻量化和13°冲击性能的提升。

(4)基于网格变形技术建立了两种工况下车轮的参数化模型，使用Isight软件集成各工况的计算软件并综合运用DOE采样、近似模型理论和NSGA-Ⅱ对车轮进行多目标优化设计，得到了Pareto前沿。在综合考虑并满足了车轮13°冲击性能的条件下选取了一个妥协解，并对比分析了优化前、后车轮各性能指标的变化，结果表明：相对于同型铸造铝合金整体式车轮，本文设计的组装式车轮减重30.65%。

(5)通过对车轮的联合拓扑优化、13°冲击性能的仿真分析和参数化建模，实现了一套基于车轮疲劳性能和13°冲击性能的结构设计流程和优化方法，为车轮多目标优化设计提供了理论和技术依据。

[1] Hirano A. Study on wheel stiffness considering balance between driving stability and weight [C]∥SAE Paper，2015-01-1755

[2] Shang D, Liu X, Shan Y, et al. Research on the stamping residual stress of steel wheel disc and its effect on the fatigue life of wheel [J]. International Journal of Fatigue, 2016, 93: 173-183.

[3] Ballo F, Frizzi R, Mastinu G, et al. Lightweight design and construction of aluminum wheels [C]∥SAE Paper, 2016-01-1575.

[4] Oery T, Sankaran R T, Nesarikar A S. Simulation and test correlation of wheel radial fatigue test [C]∥SAE Paper, 2013-01-1198.

[5] Bendsøe M P, Kikuchi N. Generating optimal topologies in structural design using a homogenization method [J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224.

[6] Jeong S H, Yoon G H, Takezawa A, et al. Development of a novel phase-field method for local stress-based shape and topology optimization [J]. Computers and Structures, 2014, 132(1): 84-98.

[7] Liu J, Ma Y. A survey of manufacturing oriented topology optimization methods [J]. Advances in Engineering Software, 2016, 100: 161-175.

[8] Deaton J D, Grandhi R V. A survey of structural and multidisciplinary continuum topology optimization: post 2000 [J]. Structural and Multidisciplinary Optimization, 2014, 49(1): 1-38.

[9] Sangree R, Carstensen J V, Gaynor A T, et al. Topology optimization as a teaching tool for undergraduate education in structural engineering [C]∥Structural Engineering Proceedings of the Structures Congress, Portland, OR，2015: 2632-2642.

[10] Zhang Z J, Jia H L, Sun J Y, et al. Application of topological optimization on aluminum alloy automobile wheel designing [J].Advanced Materials Research , 2012,562-564: 705-708.

[11] Hu J H,Liu X X, Sun H X, et al. Development and application of light-weight design of the aluminum alloy wheel [C]∥Applied Mechanics and Materials Trans Tech Publications, 2013, 310: 253-257.

[12] Xiao D, Zhang H, Liu X, et al. Novel steel wheel design based on multi-objective topology optimization [J]. Journal of Mechanical Science and Technology, 2014, 28(3): 1007-1016.

[13] 臧孟炎, 秦滔. 铝合金车轮 13°冲击试验仿真分析[J]. 机械工程学报, 2010, 46(2): 83-87.

Zang Meng-yan, Qin Tao. Simulation analysis of car A-alloy wheel 13° impact test [J]. Journal of Mechanical Engineering, 2010, 46(2): 83-87.

[14] 尹冀, 朱平, 章斯亮. 考虑应变率效应的钢制车轮冲击仿真与试验[J]. 上海交通大学学报, 2013, 47(6): 967-971.

Yin Ji, Zhu Ping, Zhang Si-liang. Simulation and experimental study of steel wheel impact test considering strain rate effect [J]. Journal of Shanghai Jiaotong University, 2013, 47(6): 967-971.

[15] Chang C L, Yang S H. Simulation of wheel impact test using finite element method [J]. Engineering Failure Analysis, 2009, 16(5): 1711-1719.

[16] 郑玉卿, 刘建峰. 基于 Abaqus 显式算法的铸铝车轮碰撞模拟[J]. 汽车工程, 2011, 33(2):152-155.

Zheng Yu-qing, Liu Jian-feng. Impact simulation of casting aluminum wheel using Abaqus/explicit [J]. Automotive Engineering, 2011, 33(2):152-155.

[17] Vinothkumar S, Srinivasan S, Nesarikar A K. Simulation and test correlation of wheel impact test [C]∥SAE Paper, 2011-28-0129.

[18] 闫胜昝, 童水光, 朱训明. 轮胎充气压力对车轮应力分布影响的数值模拟[J]. 浙江大学学报:工学版, 2009, 43(3): 565-569.

Yan Sheng-zan, Tong Shui-guang, Zhu Xun-ming. Numerical simulation on influence of tire pressure to stress distribution in wheel [J]. Journal of Zhejiang University (Engineering Science), 2009, 43(3): 565-569.

[19] Tsai G C, Huang K Y. 13° impact test analysis of aluminum alloy wheel [C]∥Advanced Materials Research, Trans Tech Publications, 2013, 631: 925-931.

[20] 张响. 铝合金车轮数字化仿真及工艺优化[D]. 浙江: 浙江大学材料与化学工程学院, 2008.

Zhang Xiang. Aluminum wheel digital simulation and process optimization [D]. Zhejiang: College of Materials and Chemical Engineering, Zhejiang University, 2008.

[21] Chauhan M R, Kotwal G, Majge A. Numerical simulation of tire and wheel assembly impact test using finite element method [C]∥SAE Paper, 2015-26-0186.

[22] 王宁, 杜林秀, 吴迪, 等. 超级钢汽车车轮强度有限元分析[J]. 东北大学学报 ：自然科学版, 2006, 27(7): 779-781.

Wang Ning, Du Lin-xiu, Wu Di, et al. FEM analysis of strength of automotive wheels made from ultra-fine grain steel [J]. Journal of Northeastern University (Natural science), 2006, 27(7): 779-781.

[23] 畅世为, 张维刚. 复合材料车轮冲击试验仿真分析[J]. 汽车工程, 2010, 32(1): 65-68.

Chang Shi-wei, Zhang Wei-gang. A simulation analysis on the impact test of composite wheel [J]. Automotive Engineering, 2010, 32(1): 65-68.

[24] Tiwari D, Arora J, Khanger R. Study of parameters affecting the impact performance of an alloy wheel and noble approach followed to improve the impact performance [C]∥SAE Paper, 2015-01-1514.

[25] Shang R, Altenhof W, Hu H, et al. Kinetic energy compensation of tire absence in numerical modeling of wheel impact testing [C]∥SAE Paper, 2005-01-1825.

[26] Stearns J,Srivatsan T S, Prakash A, et al. Modeling the mechanical response of an aluminum alloy automotive rim [J]. Materials Science and Engineering A, 2004, 366(2): 262-268.

[27] Sah S K, Bawase M A, Saraf M R. Light-weight materials and their automotive applications [C]∥SAE Paper, 2014-28-0025.

[28] Ballo F, Mastinu G, Gobbi M. Lightweight design of a racing motorcycle wheel [C]∥SAE Paper, 2016-01-1576.

[29] Collet M,Bruggi M, Duysinx P. Topology optimization for minimum weight with compliance and simplified nominal stress constraints for fatigue resistance [J]. Structural and Multidisciplinary Optimization, 2016,55(3): 1-17.

[30] Bruggi M, Duysinx P. Topology optimization for minimum weight with compliance and stress constraints [J]. Structural and Multidisciplinary Optimization, 2012, 46(3): 369-384.

[31] Rozvany G I N. On symmetry and non-uniqueness in exact topology optimization [J]. Structural and Multidisciplinary Optimization, 2011, 43(3): 297-317.

[32] 李兵. 计及复杂胎面花纹的子午线轮胎结构有限元分析[D]. 合肥: 中国科学技术大学工程科学学院, 2008.

Li Bing. Finite element structural analysis for radial tires with complex tread patterns considered [D]. Hefei: School of Engineering Science, University of Science and Technology of China, 2008.

[33] Yi G, Kim N H. Identifying Boundaries of Topology Optimization Results using basic Parametric Features [M]. New York: Springer, 2016: 1-14.

[34] Hahn Y, Cofer J I. Study of parametric and non-parametric optimization of a rotor-bearing system[C]∥Turbine Technical Conference and Exposition, American Society of Mechanical Engineers, 2014: V07AT28A001-V07AT28A001.

[35] Leifsson L, Hermannsson E, Koziel S. Optimal shape design of multi-element trawl-doors using local surrogate models [J]. Journal of Computational Science, 2015, 10: 55-62.

[36] Golzari A, Sefat M H, Jamshidi S. Development of an adaptive surrogate model for production optimization [J]. Journal of Petroleum Science and Engineering, 2015, 133: 677-688.

[37] Pan I, Das S. Kriging based surrogate modeling for fractional order control of microgrids [J]. IEEE Transactions on Smart Grid, 2015, 6(1): 36-44.

[38] Mehmani A, Chowdhury S, Messac A. Predictive quantification of surrogate model fidelity based on modal variations with sample density [J]. Structural and Multidisciplinary Optimization, 2015, 52(2): 353-373.