无线传感器网络三维节点的可行域定位

李彬,施泱,贾新春,吕晓军

(1.山西大学 数学科学学院,山西 太原 030006;2.中国铁道科学研究院,电子计算技术研究所,北京 100081)

0 引言

无线传感器网络(Wireless Sensor Network,WSN)的广泛应用使之成为21世纪最具发展前景的技术之一[1]。大多数情形,无线传感器网络在知道节点的位置信息的前提下,其侦测到的事件或采集到的数据才有参考价值。因此节点定位技术成为了无线传感器网络研究中的重要核心技术之一[2]。而受地形等因素的限制,无线传感器在实际应用中往往都分布于三维空间中。比如土壤环境监测、铁路及电网运营环境的监测等情形,都需要在大尺度范围下随机部署大量传感器。而受监测成本的影响,这些传感器中只有少部分节点装备有GPS定位装置。因此在部分节点位置已知的情形下探讨无线传感器网络节点的三维定位方法有着非常重要的现实意义。

目前针对无线传感器网络的定位通常分为两类:一种需要利用已知节点与未知节点间的距离关系(Range-Based),另一种不需要(Range-free)[3]。文献[4]提出了APIT-3D定位算法,将二维APIT定位算法推广到三维空间,有着比较理想的定位精度。但其定位精度的高低与节点密度密切相关,而且三维PIT测试有着一定的误判率。文献[5]将体积测算引入APIT-3D定位的方法中,通过体积测算来判别节点是否存在于锚节点形成四面体的内部,从而提升了节点的定位精度。但锚节点数量对此算法的定位精度和计算复杂度有着较大影响。文献[6]提出了一种改进的三维APIT算法。该算法将包含未知节点的四面体质心进行迭代,降低了网格扫描法的计算复杂程度,且定位精度有了一定的提升。文献[7]提出一种基于无线射频识别技术的室内定位算法,该算法将定位过程分为被动与主动两个阶段。在被动阶段,通过定位射频识别信标建立参考节点,用以在主动阶段进行读取比对。而在主动阶段,通过边界决策优化方法实现了移动目标的快速定位。文献[8]提出了一种基于接收信号和信号到达角度的三维目标定位方法,通过球坐标变换建立了测量值与未知位置的关系,推导出了算法的闭式解,可实现目标的快速定位。

本文提出一种基于部分节点空间位置已知(如通过GPS定位)的情况下,将未知节点可能存在的区域离散化,利用匹配算法估计无线传感器网络三维节点定位算法。

1 定位原理

需要利用距离信息来定位的算法，其测距手段主要有利用接收信息时间(70 A),利用信号接收角度(AOA)和利用接收信号强度指示值(RSSI)等几种测距方法[9-12]。

1.1 基于RSSI的定位算法分析

基于测距的定位算法通常会得到比非测距定位算法更高的定位精度,但测距技术一般需要额外的硬件支持,也就意味着更高的成本。基于RSSI的测距技术虽然不需要额外的硬件支持,但RSSI值易受到环境影响使其实际值与理论值的偏差较大,所以虽然RSSI值和距离之间理论上存在着确定的函数关系,但在实际状态下由 RSSI值所得到的节点间的距离信息并不准确。

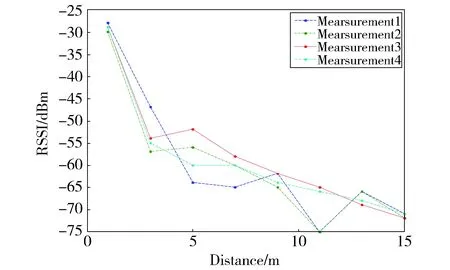
Fig.1 Relationship between distance and RSSI图1 RSSI强度随距离的变化关系实际环境曲线

图1为在相同的位置变化条件下,多次实验测量两节点间信号强度所得出的RSSI值随距离变化的曲线图。从图中可以看出,实际动态环境中RSSI值易受到外界环境干扰,其真实值将会与理论值有较大的偏差。所以虽然理论上利用RSSI值所转化得到的距离信息可以使得定位更为精确,但在实际中RSSI值只能对节点间距离进行估测。这也是我们关注非测距定位算法的原因之一。

1.2 APIT-3D定位算法

无线传感器网络节点的三维定位算法的研究有着很重要的现实意义。然而由于三维空间的复杂性,针对无线传感器网络的大多数定位算法的定位精度都不高。APIT-3D定位算法是较为经典的三维定位算法之一。

APIT-3D定位算法是将二维APIT思想扩展到三维空间中,其基本步骤是:

(1)未知节点记录所有与其可通信的锚节点位置,并任选其中4个节点组成空间四面体。

(2)若未知节点包含于该四面体内,则将这些锚节点归入到以锚节点为顶点的四面体集合内，再从可通信锚节点集中选择另一组锚节点，在所有可能组合判断结束之前重复以上步骤。

(3)使用三维网格扫描法将所有四面体集合形成的最小三维公共区域找出，然后求出此区域的质心，以此质心作为未知节点位置的估计。

Fig.2 Schematic diagram of APIT-3D图2 APIT-3D节点测试方法

三维APIT测试方法如图2所示。在图2(a)中,若节点M比对自己与节点3所收到的锚节点A,B,C,D的信号强度,对比节点M与节点3，其收到锚节点A的信号增强，而其他节点信号强度都在减弱。这意味着节点M的位置与节点3对应没有同时远离或者接近某个四面体。因而节点M是在四面体内部的。在图2(b)中,若节点M比对自己与节点2所收到的锚节点A,B,C,D的信号强度,节点M比节点2收到锚节点的信号强度都要强。这说明节点M相对于节点2靠近某个四面体。由此可知节点M在四面体外部。

APIT-3D定位算法存在几个重要缺陷:一是此方法存在误判的可能性;二是当节点密度较高时计算量增大;三是节点分布不均或较少情形下定位精度较低。

2 算法模型

2.1 极小可行域算法

定义1 可与未知节点通信的所有锚节点的公共通信范围称为可行域。

APIT-3D算法首先要找到与未知节点可通信的锚节点集,然后寻找这些锚节点通信区域形成的交集,最后用此区域的质心来估测未知节点坐标。然而不只是APIT-3D定位算法,其他质心定位算法也都需要尽可能找到一个足够精确的未知节点可能存在的空间区域,这一点也是影响到未知节点定位精度的关键。可行域中的每一点其实都可作为未知节点位置的估计。本文中给出一种可以进一步缩小可行域的算法,我们称为极小可行域算法。

为了便于理解,我们以二维情形为例说明此方法。如图3(a)中所示,未知节点与锚节点O1,O2,O3可以通信,与未知节点可通信的锚节点会形成一个公共通信范围(如图中阴影区域),改进质心算法通常以此区域的质心作为未知节点位置的估计,提高了定位精度。但这种定位算法只考虑了可通信的锚节点对未知节点定位起的作用,并未充分利用未知节点的通信信息。

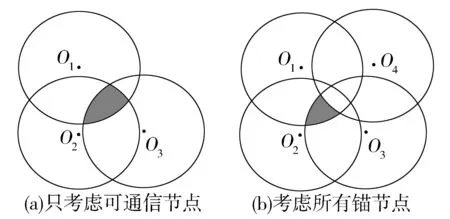
Fig.3 Schematic diagram of feasible region algorithm图3 可行域算法示意图

从图3(b)中可看出,虽然未知节点不能与锚节点O4通信,但利用锚节点O4的通信范围同样可以缩小可行域(阴影区域),以此可行域的质心估计未知节点的位置,将可提高定位精度。在图3(b)中,可行域中的节点与未知节点有相同的可通信信息。我们用0-1通信向量来表示这种可通信的性质。

定义2 设网络中有m个锚节点Oj(j=1,…,m),记T=(tj)1×m为未知节点的通信向量。

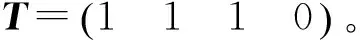
定义3 与未知节点有相同通信向量的空间位置所构成的集合称为极小可行域。

定理1 在定位未知节点时,当只得到其与锚节点可否通信的信息时,极小可行域是包含未知节点位置的最小区域。

证明不难看出,极小可行域中任一位置都与未知节点有相同的通信向量,则极小可行域中的任一位置均可能为未知节点位置;反之,若某一位置与未知节点的通信向量相同,那么由定义3可知它也一定在极小可行域中。

定位未知节点时,若能找到包含它的极小可行域将大大提高定位精度。由于锚节点在空间内常为随机分布,而极小可行域又为一空间区域,所以找出空间区域内所有与未知节点有相同通信向量的位置算法会很复杂。考虑到传感器节点的计算能力,我们将此空间区域网格离散化,选出极小可行域内足够多的离散点位置,用这些离散点系统代替可行域。

2.2 三维极小可行域定位算法

与二维极小可行域定位算法类似,假设三维空间中随机分布着若干节点,其中锚节点坐标均已知,未知节点的可行域定位算法可采用如下步骤:

设待定位节点P(x,y,z),与P可通信锚节点集{Pi(xi,yi,zi)}(i=1,2,…,k),节点通信半径为R。

节点间距为λ,则

λ称为分割细度或分辨率。这样就可在D内插入l3个比对节点(ui,vj,wk)(i,j,k=1,2,…,l)。

step3 以R为通信半径,分别讨论l3个节点的通信向量,并将之与未知节点的通信向量进行比对,选出与未知节点有相同通信向量的节点集{Qi(xi,yi,zi)}(i=1,2,…,t)。

step4 求出{Qi(xi,yi,zi)}所形成的质点系统的质心,并以质心坐标作为未知节点P(x,y,z)位置估计。

可以看出,本算法的复杂程度与分辨率λ相关,算法的复杂程度为O(l3)。分辨率越高求得的极小可行域中的点越多,定位也就越精确,但过高的分辨率也意味着更高的计算复杂度。

此外,由于本算法是在单个传感器节点上进行的,因此是一种分布式的定位方法,避免了节点间大量数据的传输而造成的能量损耗,从而延长了网络寿命。

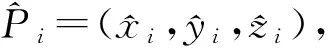
定义5 在定位算法中,为了衡量算法的定位效果,一般常用error与节点通信半径R的比值来表示精度,记为E

E=error/R.

E值越小定位效果越好。

3 实验结果分析

为了验证算法的定位性能,本文在MATLAB环境下对可行域算法和APIT-3D定位算法的定位效果进行了比对。仿真环境为长、宽、高均为100 m的空间区域。设传感器节点的通信半径R=40 m,区域D内随机分布着n个传感器节点,其中有m个锚节点,锚节点所占比例为30%,分割细度λ=2。

在仿真时,所选取的节点数量从80递增至240,重复实验50次,以实验均值进行比对。

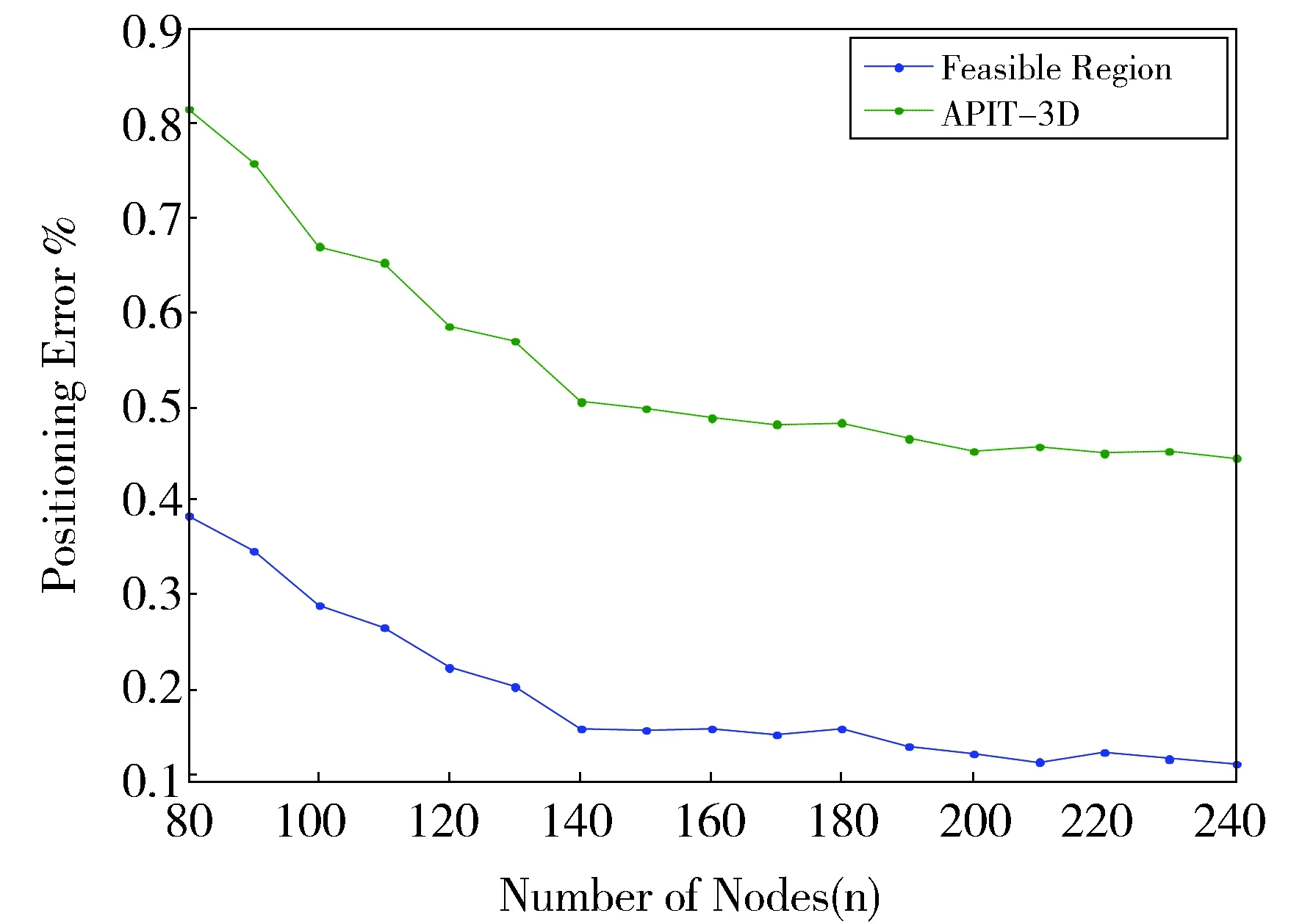
Fig.4 Effect of the number of nodes on the positioning error图4 节点数量对定位精度的影响

图4显示出节点总数量的增加可使得可行域定位算法的定位精度有一定提高,定位效果整体优于APIT-3D算法,定位效果可提升50%以上。此外,当节点数量为80时,可行域定位算法的定位精度为0.383。这说明当节点数量较少时,可行域定位算法的精度依然可靠。

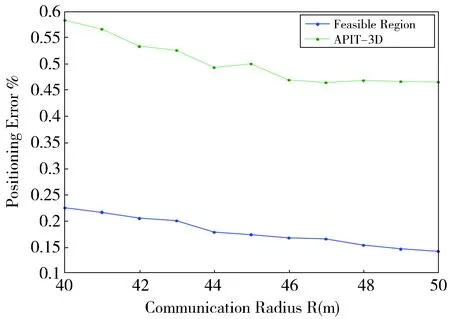
Fig.5 Effect of the communication radius on the positioning error图5 节点通信半径对定位精度的影响

在区域内随机分布节点的数量为100,锚节点所占比例为30%。实验随机生成50个网络,图5分别观察通信半径的变化对两种定位方法定位精度的影响情况。图中显示节点通信半径的增长使得未知节点集定位的平均误差也随之减小。同时,可行域定位算法的定位效果整体优于APIT-3D定位算法,相比APIT-3D定位算法的定位精度可提高60%以上。

设在100 m×100 m×100 m的空间区域内分布着120个传感器节点,其中锚节点数量为30%,节点的通信半径为30 m。对待定位节点可行域采用不同细度进行分割,分别讨论其定位精度。

Fig.6 Effect of the segmentation accuracy on the positioning error图6 分割细度对定位精度的影响

从图6中可以看出,分辨率的提升使定位误差整体趋于减小。但当分割细度小于2时,定位精度的提高并不明显,依然维持在0.22左右。这主要是由于算法是通过计算质心来求得未知节点的估计位置,即使极小可行域内插入较多的节点,其估计精度也将很难再提升。但随着细度的缩小,算法的复杂程度相应提高,这对节点的计算能力提出了挑战。所以本算法是一种适用于户外大尺度范围内的节点自定位算法。

4 结论

本文提出一种极小可行域算法用以实现无线传感网节点的空间定位。算法通过比对待定位节点与位置节点间的通信向量,求出待定位节点的极小可行域,并用极小可行域的质心作为待定位节点位置的估计。此算法是一种分布式定位算法,节点间通信消耗小,适用于户外大尺度范围的节点自定位算法。通过仿真结果可以看出,该算法有着较好的定位效果,在相同的实验条件下平均定位精度较传统APIT-3D定位算法提高约50%以上。如何与其他定位算法相结合,实现高精度、低复杂度的定位,将是我们下一步的改进方向。

[1] Naveed S,Mounir G,Kemp A H.Optimized Low Complexity Sensor Node Positioning in Wireless Sensor Networks[J].IEEESensorsJournal,2014,14(1):39-46.DOI:10.1109/JSEN.2013.2278864.

[2] Liu Y H,Yang Z,Wang X P.“Location”,Localization and Localizability [J].JournalofComputerScienceandTechnology,2010,25(2):274-297.DOI:10.1007/s11390-010-9324-2.

[3] Cheng L,Wu C,Zhang Y,etal.A Survey of Localization in Wireless Sensor Network[J].InternationalJournalofDistributedSensorNetworks,2012,8(12):962523(1-12).DOI: 10.1155/2012/962523.

[4] 刘玉恒,蒲菊华,赫阳,等.无线传感网络三维自身定位方法[J].北京航空航天大学学报,2008,34(6):647-651.DOI:10.13700/j.bh.1001-5965.2008.06.028.

[5] Shu J,Yan C,Liu L.Improved Three-dimensional Localization Algorithm Based on Volume Test Scan for Wireless Sensor Networks[J].TheJournalofChinaUniversitiesofPostsandTelecommunications,October，2012:1-6.DOI:10.1016/S1005-8885(11)60452-4.

[6] 胡伟,朱西平,文红,等.基于四面体质心迭代的三维APIT定位算法研究[J].传感技术学报,2013,26(10):1432-1436.DOI:10.3969/j.issn.1004-1699.2013.10.022.

[7] Maneesilp J.RFID Support for Accurate 3D Localization[J].IEEETransactionsonComputers,2013,62(7)：1447-1459.DOI: 10.1109/TC.2012.83.

[8] Tomic S,Beko M,Dinis R,etal.A Closed-Form Solution for RSS/AoA Target Localization by Spherical Coordinates Conversion[J].IEEEWirelessCommunicationsLetters,2016,5(6):680-683.DOI: 10.1109/LWC.2016.2615614.

[9] Martinelli F.A Robot Localization System Combining Rssi and Phase Shift in Uhf-rfid Signals[J].IEEETransactionsonControlSystemsTechnology,2015,23(5):1782-1796.DOI: 10.1109/TCST.2014.2386777.

[10] Beaudeau J P,Bugallo M F,Djuric P M.RSSI-based Multi-target Tracking by Cooperative Agents using Fusion of Cross-target Information[J].IEEETransactionsonSignalProcess,2015,63(19):5033-5044.DOI: 10.1109/TSP.2015.2448530.

[11] Tomic S,Beko M,Dinis R.RSS-Based Localization in Wireless Sensor Networks Using Convex Relaxation:Non-cooperative and Cooperative Schemes[J].IEEETransactionsonVehicularTechnology,2015,64(5):2037-2050.DOI: 10.1109/TVT.2014.2334397.

[12] 刘志平，朱丹彤，杨磊，等.狭长受限空间锚节点定位的测距仪双侧自由设站法[J].传感技术学报，2017(2)：1700-1705.