考虑钻具磨损内热源的深水钻井循环温度场研究*

刘文成 赵丹汇 赵 琥 郭朝红 姜玉雁 李志刚

(1.中海油田服务股份有限公司 河北三河 065201； 2.中国科学院工程热物理研究所 北京 100190)

井下循环温度分布是进行井壁稳定性分析和解释井筒呼吸效应的关键参数，掌握钻井作业过程中井内循环温度分布及其变化规律，对井控和安全快速钻进有重要意义。自20世纪60年代以来，国内外学者针对井下循环温度进行了研究，建立了不同的理论模型和算法[1-6]，但这些研究对机械磨损热源考虑较简单，且均针对地面钻井或固井，对于深水钻井循环温度预测的研究资料较少。

Ward等[7-8]曾对平均水深1 200 m的深水钻井循环过程进行了现场温度测量，发现井内循环流体受到海水对流的作用明显冷却，流体流变性发生变化，显著增大了循环压力，对钻井作业的安全性有很大影响。赵琥 等[9]曾建立井下循环瞬态传热模型，对深水钻进过程的循环温度场进行研究，但未分析钻进过程中钻具机械磨损对井下循环温度的影响。虽然有学者曾针对深水钻井温度场进行建模计算[10]，但该模型仅考虑了钻头水眼节流产生的机械磨损，并未考虑钻具旋转带来的机械磨损热源，计算结果也未得到实测数据的验证。因此，对深水钻井循环温度场进行准确的预测，还需要更深入的研究。

本文考虑钻具机械磨损内热源的影响，建立了深水钻井循环温度场计算模型，并将计算结果与现场实测数据进行了对比分析，结果表明本文模型具有较高的准确性，可为深水钻井循环温度场的计算预测提供借鉴。

1 瞬态传热模型的建立

1.1 基本假设

1) 套管和钻杆居中度100%，环空间隙均匀，井型为直井；

2) 循环流体、海水及地层岩石的比热、导热系数等热物性参数不随温度、压力变化；

3) 管柱和环空的尺寸与地层空间相比非常小，所以假设管柱内和环空内的流体是一维非稳态传热。

1.2 控制方程

根据以上假设，取管柱内流体、钻杆管壁、环空内流体作为研究对象，沿井深方向将管柱内流体、管柱壁、环空流体分别划分为n个控制单元。根据热力学第一定律，由外界进入单元体的净热量与外界对单元体所做的功之和等于单元体内能的增量，推导出不同单元内的温度场控制方程如下。

管柱内流体：

(1)

管柱壁：

(2)

环空流体：

(3)

式(1)～(3)中：G为循环流体体积流量，m3/s；p为单位长度压力损失，Pa/m；S为机械磨损热源项，W/m；c为比热，J/(kg·K)；T为温度，K；t为时间，s；z为控制单元长度，m；r为半径，m；h为对流换热系数，w/(m2·K)；k为导热系数，w/(m·K)；ρ为密度，kg/m3；下标p、w、a、we、ci、co分别代表管柱内、管柱壁、环空内、井壁、管柱壁内侧、管柱壁外侧。式(1)～(3)是针对地层区域推导出的传热模型，与现有研究资料[2-5]相比，该计算模型考虑了流体的轴向导热、筒壁的径向导热等因素的影响。

海域内各控制单元的传热模型与式(1)～(3)形式相同，但其中一些参数需要由海水换热条件来确定。深水作业时通常是海底注入增压流量促进环空返液，此时环空内流体的流量为循环流量与增压流量之和。对于有隔水管的工况，管柱内流体和管柱壁的控制方程与式(1)、(2)相同，环空流体的控制方程需将式(3)中的代表井壁的参数(下标为we)改为隔水管的相应参数，隔水管的温度由海水对流边界条件来确定；对于无隔水管的工况，管柱内流体的控制方程与式(1)相同，但管柱壁的控制方程需将式(2)中环空温度Ta改为海水温度Ts，环空对流换热系数hco改为海水对流换热系数hs。

1.3 热源项的计算

在钻井作业过程中，钻井泵和旋转系统分别向钻井系统提供水力学能量和机械能量,其中一些能量用于破碎岩石和携带岩屑返出井筒，剩余的能量均以热量的形式耗散掉[11]，而这些耗散的热量直接影响井下温度分布。热源项主要包括3部分：由钻井液流动黏性耗散产生的热量、钻头水眼节流磨损产生的热量和钻头破岩产生的热量。

钻井液在管柱内及环空内流动时，由于钻杆旋转的作用会形成非牛顿流体的螺旋流动，黏性耗散产生的热量主要表现在钻井液循环过程中摩阻压降的大小。Ahmed等[12]利用量纲分析方法建立了非牛顿流体层流流动时钻柱旋转与非旋转时摩阻压降比值的经验校正方法，其中旋转摩阻压降比值pLR定义为

(4)

(5)

(6)

kr=Dco/Dwe

(7)

式(4)～(7)中：τy为赫巴流体的屈服值，Pa；ua为轴向平均流速，m/s；εave为平均无量纲偏心率；n为流性指数；Ta为泰勒数，比较离心力与黏滞力的作用大小；Ei为有效偏心距，m；Li为井段长度，m；MD为井深总长，m；Rea为轴向流动雷诺数；kr为钻杆外径与井眼直径的比值；Dco为钻杆外径，m；Dwe为井眼直径，m；ω为钻头转速，rad/s；μ为流体表观黏度，Pa·s;m为井段数；i为自然数，i=1，2，…，m。

钻头水眼节流磨损产生热量导致的压力损失模型为

(8)

式(8)中：Δp为钻头喷嘴压力降，Pa；ρ为钻井液密度，kg/m3，Q为泵排量m3/s；C代表喷嘴流量系数，无因次；A为钻头水口总面积，m2。钻头喷嘴流量系数取值范围为 0.914～0.963[13]，工程应用可以取值0.95。

钻头破岩产生的热量为

dQdb=fdbFdburldt

(9)

其中

url=πDdbω

式(9)中：dQdb为摩擦功，J；fdb为摩擦系数；Fdb为钻压，N；url为钻头旋转线速度，m/s；Ddb为钻头平均直径，m；ω为转速，rad/s。

1.4 对流换热系数的计算

管柱内及环空内非牛顿流体的对流换热系数普遍采用Keller等推荐的计算方法[13]，并没有考虑钻柱旋转对流体流动产生的影响。井壁或隔水管不动，钻杆旋转时会在环形空间内形成螺旋流[14]，转速较低时为定常螺旋层流，转速增大后会产生Taylor涡，流动更为复杂，且对流传热作用明显。有很多学者针对螺旋流的流动特性，利用等效雷诺数对努谢尔数进行了修正[15-16]，即

(10)

(11)

式(10)～(11)中：Pr为螺旋流体普朗特数；ueff为等效流速，m/s；De为流道当量直径，m;uaxial为轴向流速，m/s；Reeff为等效流速对应的非牛顿流体等效雷诺数；α为旋转流动对换热影响的权重系数，取值范围为0.25～1；β、γ为实验确定的经验系数，本文取β=0.8、γ=0.4。当轴向流动为紊流时，环形旋转流对传热的贡献相对较小，α一般取0.25～0.6；当轴向流动为层流时，环形旋转流动对传热的贡献较大，α一般取0.8～1。钻井作业过程中，管柱内流体通常为紊流状态，而环空流体通常为层流，所以管柱内流体建议取0.5，环空内流体建议取1。

隔水管外侧或管柱外侧为海水对流边界条件。海水为牛顿流体，其外掠圆管的努谢尔数计算方法为[17]

(12)

式(12)中：Res为海水雷诺数；Prs为海水普朗特数；c、n为系数，根据雷诺数取值。

1.5 初始条件和边界条件

1)地层区域内，管内外流体、管柱壁、井壁的初始温度为原始地层静止温度,即

Tp|e,t=0=Tw|e,t=0=Ta|e,t=0=Tei=Tf+Gez

(13)

式(13)中：Tei为地层静止温度，K；Tf为地表静止温度，K；Ge为地温梯度，℃/100 m。

2) 海域内，管内外流体、管壁的初始温度为初始海水温度,即

Tp|f,t=0=Tw|f,t=0=Ta|f,t=0=Tg|f,t=0=Tsi

(14)

式(14)中：Tg为隔水管温度，K；Tsi为海水层初始温度，K。

3) 管柱内流体的入口温度为已知测量值,即

Tp|z=0=Tpi

(15)

4) 管内流体、环空流体及管柱壁在井底(z=zd)温度相等，即

Tp|z=zd=Tw|z=zd=Ta|z=zd

(16)

5) 采用Hansan&Kabir提出的一维准稳态传热模型[1]来计算井壁温度，地层与井壁的换热量为

(17)

当地层为恒定热流条件时，无量纲时间参数f(t)为

(18)

其中

(19)

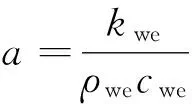
(20)

根据井壁内部导热与环空流体对流换热平衡的边界条件，可得第j时刻井壁温度为

(21)

2 模型验证及影响因素分析

采用南海深水区LS25-1-2井的钻井实测数据进行模型验证。该井隔水导管下深988.3 m，表层套管下深2 025 m，钻头尺寸φ0.444 5 m, 钻杆尺寸φ0.149 2 m,完钻深度3 430 m。作业现场地温梯度3.61 ℃/100 m，海水温跃层一般在200 m左右[10]，因此设海水在200 m深度内从28 ℃的表层温度线性降低到3.8 ℃，之后保持不变直到海底。平均钻速约为0.007 m/s，井深达到2 750 m时停止钻进，共耗时约30 h。钻井液入口温度保持22 ℃不变，循环流量为4 550 L/min，海底补充的增压流量为2 000 L/min。经实验测量，循环钻井液的物性参数如表1所示。

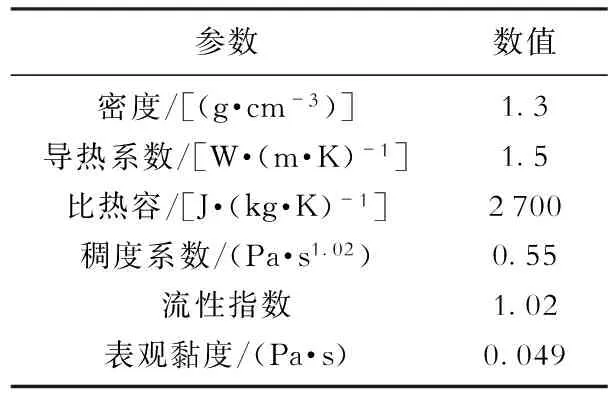
表1 LS25-1-2井钻井液物性参数Table 1 Property parameters of drilling fluid in Well LS25-1-2

考虑钻具机械磨损及流动磨损带来的内热源以及螺旋流动的影响，根据所建立的深水钻井计算模型，计算得到该井井底循环温度随时间的变化曲线，并与实测温度值进行比较，如图1所示。由图1可以看出，本文模型计算结果与实测随钻温度比较吻合，证明本文模型具有较高的精度。

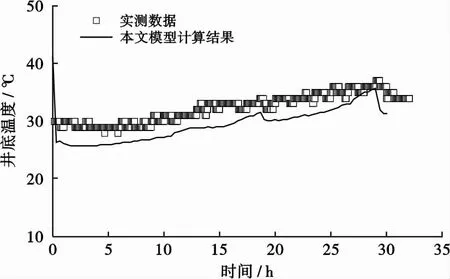
图1 LS25-1-2井模型计算井底循环温度与实测温度 数据的比较Fig .1 Comparison of bottom hole circulating temperature between calculation and measured data in Well LS25-1-2

根据实测钻压、转速、扭矩数据(图2)，沿井深分为2 000～2 500 m、2 500～2 700 m、2 700～2 800 m等3个阶段，根据数据变化特征分别取平均值或按线性变化取值，结合式(4)～(9)计算钻具旋转产生的流动摩阻及钻头磨损，并采用式(10)～(11)计算井内流体的对流换热系数，代入温度模型进行计算，结果如图3所示。从图3可以看出，该井钻进过程中若不考虑钻具磨损带来的热源影响，则计算误差非常大，比实测值低10 ℃左右；若不考虑钻柱旋转对换热系数的影响，则计算结果要比实测温度低5 ℃左右。因此，钻具机械磨损以及钻具旋转对流体换热强化的作用在钻井循环过程中是非常重要的影响因素，在分析计算井下循环温度时必须予以考虑。

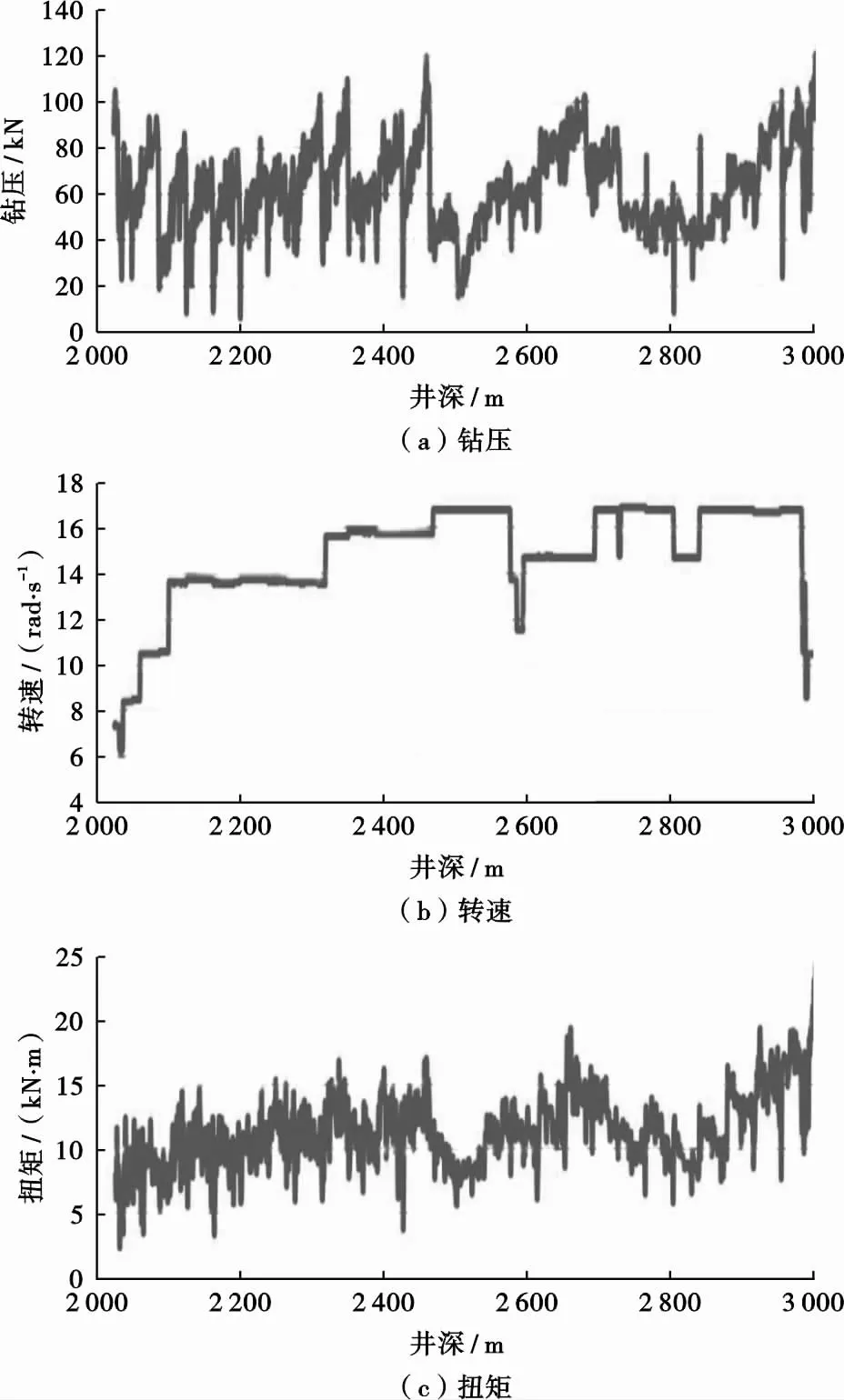
图2 LS25-1-2井钻压、转速、扭矩随井深的变化曲线Fig .2 Curves of bit pressure，drilling velocity and torque at different depths of Well LS25-1-2

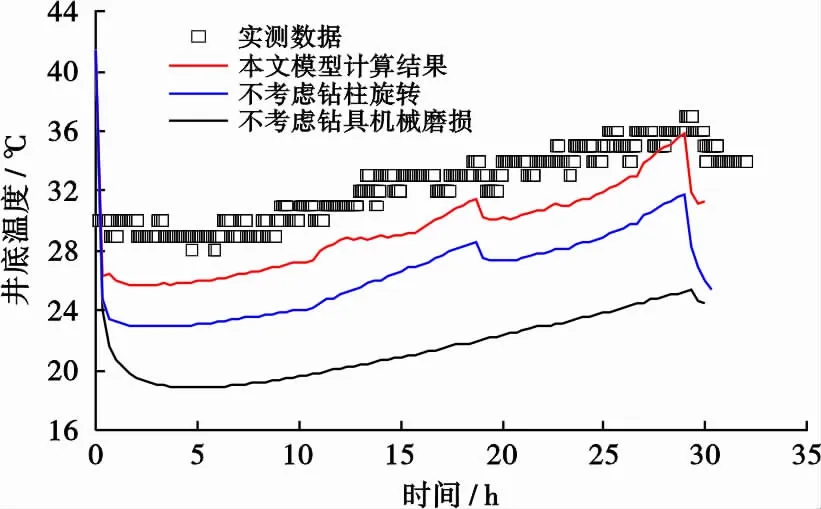
图3 钻具磨损及旋转对LS25-1-2井井底温度的影响Fig .3 Influences of drilling rig friction and rotation on bottom-hole temperature of Well LS25-1-2

图4为有无增压流量条件下计算得到的该井环空出口温度变化曲线。从图4可以看出，计算时若不考虑海底增压流量，则环空出口处的温度较高，达到25～30 ℃，高于实测温度20 ℃；若考虑海底增压流量2 000 L/min时,则环空出口温度大幅下降，约为18～20 ℃，与实测温度比较吻合。因此，在计算分析环空出口温度时必须考虑海底增压流量的影响。

图4 增压流量对LS25-1-2井环空出口温度的影响Fig .4 Influence of boosted flow on the outlet temperature of annulus in Well LS25-1-2

3 结论

1) 考虑钻具机械磨损与流动磨损带来的内热源以及螺旋流动的影响，建立了深水钻井循环温度场计算模型，该模型具有较高的计算精度，与实测数据吻合度较高。

2) 计算分析结果表明，钻头钻进磨损等带来的机械磨损热源及钻柱旋转的强化对流过程对井底循环温度影响很大，因此井底循环温度计算必须考虑钻柱旋转及钻头的机械磨损；深水钻井作业时增压流量对环空出口温度的影响较大，因此环空出口温度的计算分析必须予以考虑。

[1] KABIR C S,HASAN A R,KOUBA G E,et al.Determining circulation fluid temperature in drilling,workover,and well-control operations[J].SPE Drilling & Completion,1996,11(2):74-79.

[2] 钟兵，方铎，施太和.井内温度影响因素的敏感性分析[J].天然气工业，2000,20(2)：57-60.ZHONG Bing,FANG Duo,SHI Taihe.Sensibility analysis of the factors affecting temperature in well bore [J].Natural Gas Industry,2000,20(2):57-60.

[3] 易灿，闫振来，郭磊.井下循环温度及其影响因素的数值模拟研究[J].石油钻探技术，2007,35(6)：47-49.YI Can,YAN Zhenlai,GUO Lei.Numerical simulation of circulating temperature and it’s impacting parameters [J].Petroleum Drilling Techniques,2007,35(6):47-49.

[4] 何世明，尹成，徐壁华，等.确定注水泥与钻井过程中井内循环温度的数学模型[J].天然气工业，2002,22(1)：42-45. HE Shiming,YIN Cheng,XU Bihua,et al.Mathematical model of determining borehole circulating temperatures in cementing and drilling processes [J].Natural Gas Industry,2002,22(1):42-45.

[5] 何世明，何平，尹成，等.井下循环温度模型及其敏感性分析[J].西南石油学院学报，2002，24(1)：57-60.HE Shiming,HE Ping,YIN Cheng,et al.A wellbore temperature model & it’s parametric sensitivity analysis [J].Journal of Southwest Petroleum Institute,2002,24(1):57-60.

[6] 李梦博，柳贡慧，李军，等.考虑非牛顿流体螺旋流动的钻进井筒温度场研究[J].石油钻探技术，2014,42(5)：74-79.LI Mengbo,LIU Gonghui,LI Jun,et al.Research on wellbore temperature field with helical flow of non-Newtonian fluids in drilling operation [J].Petroleum Drilling Techniques,2014,42(5):74-79.

[7] WARD M,GRANBERRY V,CAMPOS G,et al.A joint industry project to assess circulating temperatures in deepwater wells [C].SPE Annual Technical Conference and Exhibition,New Orleans,Louisiana,2001.

[8] WARD M,GRANBERRY V,CAMPOS G,et al.A joint industry project to assess circulating temperatures in deepwater wells [J].SPE Drilling & Completion,2003,18(2):133-137.

[9] 赵琥，刘文成，赵丹汇，等.深水钻井作业井下循环温度场预测[J].中国海上油气，2017，29(3)：78-84.DOI:10.11935/j.issn.1673-1506.2017.03.013.ZHAO Hu,LIU Wencheng,ZHAO Danhui,et al.Prediction of temperature distribution in wellbores during circulation in deep water drilling operations[J].China Offshore Oil and Gas,2017,29(3):78-84.DOI:10.11935/j.issn.1673-1506.2017.03.013.

[10] 高永海，孙宝江，王志远，等.深水钻探井筒温度场的计算与分析[J].中国石油大学学报(自然科学版)，2008,32(2)：58-62.GAO Yonghai,SUN Baojiang,WANG Zhiyuan,et al.Calculation and analysis of wellbore temperature field in deepwater drilling [J].Journal of China University of Petroleum,2008,32(2):58-62.

[11] GONZALEZ M E,BLOYS J B,LOFTON J E.Increasing effective fracture gradients by managing wellbore temperatures[R].IADC/SPE 87217,2004.

[12] AHMED R M,ENFIS M S,KHEIR H M E.The effect of drillstring rotation on equivalent circulation density：modeling and analysis of field measurements [R].SPE 135587,2010.

[13] 尹文斌.钻井液水力参数优化设计及软件的研制[D].北京：中国地质大学(北京)，2005.YIN Wenbin.Drilling fluid hydraulic parameter optimum design & the development of software system [D].Beijing:China University of Geosciences,2005.

[14] KELLER H H,COUCH E J，BERRY PM.Temperature distribution in circulating mud columns [J].SPE Journal,1973,13(1):23-30.

[15] FENOT M,BERTIN Y,DORIGNAC E,et al.A review of heat transfer between concentric rotating cylinders with or without axial flow [J].International Journal of Thermal Sciences,2011,50(7):1138-1155.

[16] GAZLEY C.Heat transfer characteristics of the rotational and axial flow between concentric cylinders [ J].Journal of Heat Transfer,1958,80(1):79-90.

[17] 杨世铭.传热学[M].北京：高等教育出版社，2007.