交流绕组理论的原概念和新术语及其关系
2018-03-09I:
I:
程小华
(华南理工大学电力学院,广东广州 510640)
0 引言
交流绕组理论中的术语存在下列四个问题:(1)原概念不明。原概念就是最基本概念,其它概念均可基于它们导出。(2)有些术语命名不够准确;(3)有些术语命名虽准确,但字数过多;(4)有些术语尚未命名。譬如,“相带”这个术语命名就不够准确,应该是“极相带”,即“每极每相下的地带”。关于这一点,文献[1]有详细论述。“每相串联匝数”也不够准确,详见本文2.2节的分析。“每极每相槽数”这个术语长达6个字,一般术语超过4个字就有过长之嫌。给齿谐波下定义时所涉及的“每对极下的槽数”,一方面长达7个字,另一方面,根本不像一个术语,因此,可以认为这根本不能算作一个术语,即术语尚未命名。这些问题均参见文献[1-15]。本文试图解决以上问题。
说明:在不至混淆的情况下,本文不区别“概念”和“术语”。为了简洁,电动势简称为电势,磁动势简称为磁势,电角度简称为电角。
1 六个原概念
1.1 原概念的意义
交流绕组存在6个原概念,即最基本的概念: 极、相、槽、层、支、根。其它概念都可以基于这六个概念导出。
极,就是磁极。相,就是电相。槽,就是定子或转子的槽,包括槽形、槽数等。层,就是绕组的层。支,就是相绕组的并联支路。根,就是导体的单位,乃是绕组最基本的组成要素。一匝线圈含有两根导体。
极的取值为2,4,6,8,等偶数。相的取值一般为3,1,偶尔为6。文献[16]提到6相绕组。槽的取值则较为复杂,一般三相绕组的槽数为36,48,72,等。单相绕组的槽数为18,22,24,等。层的取值一般为1或2,取1就是单层绕组,取2就是双层绕组。偶尔会遇到单双层混合绕组。支的取值一般为自然数1,2,3,等。交流绕组的最大并联支路数与绕组的层数有关,单层绕组的最大并联支路数一般为极对数,双层绕组的最大并联支路数为极数。根的取值与槽数有关,每槽导体根数乘以槽数就是导体总根数。
1.2 支匝数
由“根”很容易引出“匝”。两根导体在端部相连即构成匝。《电机学》中经常出现“每相串联匝数”,譬如相电势有效值公式中、相磁势幅值公式中等。这一术语曾经给我带来困扰。第一次碰到这一术语时,我心里就打鼓,究竟什么是“每相串联匝数”呢?相绕组中每一条支路的匝数不都是串联着的吗?难道还有并联的匝数?所以,我把它理解成每相各条支路匝数的总和,因为它们属于同一相,而且都是串联着的。虽然早就明白它要表达的是什么意思了,但总觉着不够贴切。现在,总算找到解决办法了。那就是,引入一个术语“支”。“每相串联匝数”不就是想表达“每条支路的匝数”吗?进一步,“每条支路的匝数”可以简称为“每支匝数”,或者“支匝数”。“支匝数”的概念,简明扼要,可谓言简意赅,一目了然,不会引起误解。
2 几个新术语
本文引进几个新术语-以阶、方、带为主导。
2.1 阶
2.1.1 阶的定义
“阶”定义为“极对”,或者“对极”。阶数就是极对数。
2.1.2 阶槽数
引入“阶”的概念,有两层考虑:(1)“阶”是一个可以反映事物复杂性的一个比较抽象的概念。行列式、矩阵、微分方程、导数等,都有阶的概念。一阶绕组就是一对极的绕组,二阶绕组就是两对极的绕组。显然,两对极的绕组比一对极的绕组复杂。因此,阶的概念也反映了绕组的复杂性。(2)会给涉及“极对”、“对极”的概念带来省字、上口而且好记的好处。譬如,引言中提到的“每对极下的槽数”,引入“阶”这一术语后,可以称为“每阶槽数”,并且,可简称为“阶槽数”,不仅省字、上口、好记,而且变得像一个术语了。
2.1.3 槽谐波
顺便指出,齿谐波的定义为:“与每对极下的槽数有关的谐波叫齿谐波”。引入“阶”的概念,并且把“齿谐波”改为“槽谐波”,那么,该定义就变为:“与每阶槽数有关的谐波叫槽谐波”,比原来的定义好多了。第一,新定义把“槽谐波”与“每阶槽数”这一术语紧密关联,把记忆“槽谐波”概念变为记忆“每阶槽数”这一术语;第二,原定义前面说“槽”,后面却说“齿”,前后不一,很别扭,虽然齿数等于槽数,但毕竟拐了一下。新定义前后一致,自然多了;第三,槽谐波就是由于开“槽”而引起的。这就使得“槽谐波”这一概念可以顾名思义-便于理解、记忆。这一点很重要,因为交流绕组理论之概念难而多,非常容易搞错、遗忘。
2.2 方
2.2.1 方的定义
“方”定义为“从内部观察绕组而得到的相”,简称为“内相”。
方即内相。通常的相是外相。方与相一样,都是描述绕组整体属性的量。
方,也就是文献[16]第327页所谓的“从电机内部看”的相。文献[16]第327页下半页一连出现4次“从电机内部看”。这就是由于没有定义合适的术语,而导致不应有的繁琐。
方数,等于相数的两倍。因此,方数,就是“倍相”,或者“相倍”。六相绕组的方数为12,三相绕组的方数为6,单相电机(两相绕组)的方数为4。
2.2.2 方槽数
引入“方”的概念,有两层考虑:(1)作为“内部相”,方与“外部相”相对应。(2)在推导多种槽漏抗公式时,会碰到pq组合。这个pq,其实就是每方槽数,即Q/(2m),m是相数。如果没有引入方的概念,那么对pq组合的描述较为困难。因此有:2pq是每相槽数,pq是每方槽数。
可见:方槽数乃相槽数之半;方数乃相数两倍。
2.3 带
2.3.1 带的定义
“带”定义为“每极每相下的地带”,即文献[1]所称的“极相带”,也就是《电机学》流行教科书上所说的“相带”。
2.3.2 两个描述带宽的术语:带槽数、带电角
引入“带”的概念,有两层考虑:(1)可以简化一些旧的术语。(2)可以方便引入新术语。
关于简化旧术语。譬如,“每极每相槽数”可以简为“每带槽数”,或者“带槽数”。
带宽电角简称带电角,是用电角来描述的带宽。显然,带电角等于槽电角乘以带槽数。槽电角是槽距电角的简称,是槽宽的电角描述。
2.3.3 带谐波
文献[16]第331页提到:空间对称分布的相绕组由基波电流产生的合成磁势只存在下列次数的谐波
ν′=∓(μn∓1),(式中,n=0,1,2,3,…,∞;两个∓同正同负)
(1)
当n=0时,可求得ν′=+1,说明合成磁势的基波是一顺转波。
对空间分布120°相带绕组,以μ=3代入式(1)可得其磁势谐波含量为
ν′=∓(3n∓1)=+1;-2,+4;-5,+7;-8,+10;…;
(2)
对空间分布60°相带绕组,以μ=6代入式(1)可得其磁势谐波含量为ν′=∓(6n∓1)=+1;-5,+7;-11,+13;-17,+19;…;
(3)
对空间分布30°相带绕组,以μ=12代入式(1)可得其磁势谐波含量为
ν′=∓(12n∓1)=+1;-11,+13;-23,+25;-35,+37;…;
(4)
说明:在不影响含义正确的前提下,本文引用时对有关文字、符号作了必要调整。另外,为尊重原文,“相带”这一并不严谨的术语仍然照抄如上。
必须注意:式(1)中的μ表示“对称绕组在空间分布的相数”,属于内部相数。这个相数与通常所说的绕组相数不相同。前者是从绕组内部的空间分布来观察得到的相数,后者是从绕组外部的引出线来观察得到的相数,是外部相数。对空间分布120°相带绕组,二者相同,内外都是3相;对空间分布60°、30°相带绕组,内部相数都是外部相数的2倍。
还可以把单相电机绕组也包含进来,那就是:对空间分布90°相带绕组,以μ=4代入式(1)可得其磁势谐波含量为
ν′=∓(4n∓1)=+1;-3,+5;-7,+9;-11,+13;…;
(5)
这里请注意:单相电机绕组比较复杂。从绕组内部的空间分布来观察时,为4相绕组;从绕组外部的出线来观察时,为两相绕组;从绕组所接电源来观察时,为单相绕组。“单相”电机的命名,正是来自于这最后一点。
实际上,式(1)中的μ(对称绕组在空间分布的相数)就是“每对极下的带数”,亦即“每阶带数”。式(2)、式(3)、式(4)、式(5)所展示的谐波,可以归纳为“与每阶带数有关的谐波”。
与“槽谐波”定义为“与每阶槽数有关的谐波”比较,非常自然地想到新术语:“带谐波”-“与每阶带数有关的谐波”,带谐波即通常所称的“相带谐波”。
2.3.4 槽谐波、带谐波的关系
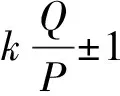
2.4 举例说明“极、相、槽和阶、方、带”概念
下面以一个Q槽4极3相60°相带的定子绕组分带展开示意图(见图1)来说明“极、相、槽和阶、方、带”的概念。图1中槽数Q一般为72、54、36等3的倍数。
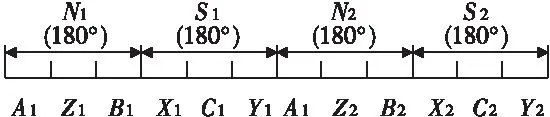
图1Q槽4极3相60°相带的定子绕组分带展开示意图
图1所示绕组,有4极(N1S1N2S2)、3相(ABC)、Q槽;有2阶(N1S1是一阶,N2S2是一阶)、6方(AZBXCY)、12带(A1Z1B1X1C1Y1和A2Z2B2X2C2Y2)。
3 结语
本文梳理出交流绕组理论的6个原概念:极、相、槽、层、支、根,引入了11个新术语:阶、方、带、阶槽数、阶带数(等于方数)、槽谐波、带谐波、支匝数、带槽数、槽电角、带电角。
最重要的新术语是阶、方、带三个,它们与原有的三个术语极、相、槽构成某种对应。
新术语的特点是,言简意赅,一目了然,既便于理解,又便于记忆。
[1] 程小华.对部分教科书中“电枢反应”和“相带”概念的辩证[J].微电机,2009.2.
[2] 许实章.电机学下册[M].北京:机械工业出版社,1981.1.
[3] 辜承林,陈乔夫,熊永前.电机学[M].武汉:华中科技大学出版社,2010.3.
[4] 吴大榕.电机学上册[M].北京:电力工业出版社,1978.
[5] 汤蕴璆,史乃.电机学[M].北京:机械工业出版社,2005.2.
[6] 陈世元.电机学[M].北京:机械工业出版社,2008.
[7] 周顺荣.电机学[M].北京:科学出版社,2002.
[8] 潘再平,章玮,陈敏祥.电机学[M].杭州:浙江大学出版社,2008.
[9] 徐德淦.电机学[M].北京:机械工业出版社,2004.
[10] 王秀和.电机学[M].北京:机械工业出版社,
2009.
[11] 戴文进,徐龙权.电机学[M].北京:清华大学出版社,2008.
[12] 张广溢,郭前岗.电机学[M].重庆:重庆大学出版社,2002.1.
[13] 李发海,朱东起.电机学[M].北京:科学出版社,2013.5.
[14] 刘慧娟,范瑜.电机学(英汉双语)[M].北京:机械工业出版社,2014.1.
[15] 阎治安,崔新艺,苏少平.电机学[M].西安:西安交通大学出版社,2006.2.
[16] 许实章.交流电机的绕组理论[M].北京:机械工业出版社,1985.
