平开门窗锁闭器对PVC建筑门窗变形性能的影响

阎玉芹 ，赵宗凯 ，杨英豪 ，马绿洲 ，高鹏刚

[1.山东建筑大学门窗与幕墙研究所，山东 济南 250101；2.山东电力研究院，山东 济南 250001；3.亚萨合莱国强（山东）五金有限公司，山东 乐陵 253600]

0 前言

五金件是门窗系统不可或缺的组成部分，五金件产品自身质量及安装使用方法对门窗的各项物理性能指标有着重要影响。目前，关于门窗物理性的研究主要集中在型材结构、玻璃结构、五金件产品自身质量等方面，对于五金件在安装使用方面对门窗性能的影响研究较少。本文分析研究了塑料平开门窗锁闭器锁闭点在门窗系统中的配置数量和安装位置对风载荷作用下门窗变形性能的影响。以塑料平开门为研究对象，在门规格尺寸确定、荷载相同的条件下，利用ANSYS软件中的 Workbench模块对在风荷载作用下门窗锁闭器锁闭点数量不同，以及锁闭器锁闭点安装位置不同2种情况下门的变形量进行了模拟分析研究。以期为平开门窗锁闭器锁闭点数量的选择、锁闭器锁闭点安装位置的确定提供理论依据。

1 锁闭器的配置对平开门窗变形性能的影响

1.1 模型设计

以常用的塑料平开门为模拟研究对象，其截面形式如图1所示。平开门宽1000 mm，高2200 mm，玻璃为5+9A+5钢化中空玻璃，型材五金槽口为欧标U槽，窗扇用3个标准合页与窗框连接。

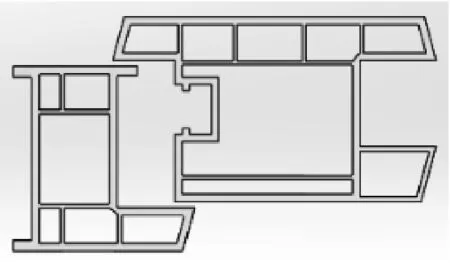
图1 塑料平开门的截面图

为了模拟分析锁闭器锁闭点数量不同对平开门窗变形性能的影响，我们选择建筑上常用的1个、2个、3个和5个锁闭点的4种锁闭器（见图2）进行模拟分析，研究采用不同数量锁闭点的锁闭器的平开门在风荷载作用下的变形情况。

图2 2种锁闭器示意

为了模拟分析锁闭器锁闭点安装位置不同对平开门窗变形性能的影响，对2个、3个和5个锁闭点锁闭器在锁闭点分布位置不同的情况下进行模拟分析（见图3）。分析2个锁闭点锁闭器时，分别将锁闭点根据图3（a）中的位置①、②、③、④、⑤五种情况对称分布在平开门上，模拟分析这5种情况下平开门在风荷载作用下的变形情况。对于3个锁闭点锁闭器，假定中间一个锁闭点的位置固定不变，分别将两边的锁闭点根据图3（b）中①、②、③、④、⑤5种情况对称分布在平开门上，模拟分析这5种情况下平开门在风荷载作用下的变形情况。对于5个锁闭点锁闭器，假定中间一个锁闭点和上下框处的锁闭点位置固定不变，分别将边框两端的锁闭点根据图3（b）中③和⑤2种情况对称分布在平开门上，模拟分析这2种情况下平开门在风荷载作用下的变形情况。

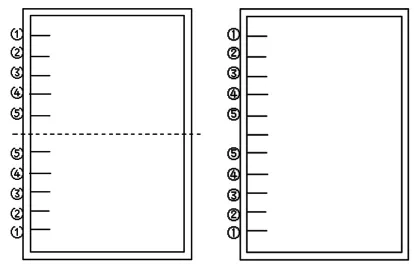
图3 锁闭点位置分布示意

1.2 有限元模拟分析

1.2.1 模型建立

（1）建模：根据塑料平开门规格尺寸和截面形状在Solidworks中创建塑料平开门三维模型（如图4所示），选用适用于欧标U槽的锁闭器，在三维模型创建过程中，根据锁闭器锁闭点数量不同，共创建了4个塑料平开门的三维模型，以.x_t的形式保存，导入ANSYS Workbench。在模型创建的过程中，以mm为长度单位。

图4 塑料平开门三维模型

（2）材料属性：门框、扇材料为PVC，五金件以及钢衬的材料为结构钢。

（3）网格划分：选用4单元的186网格划分，对局部更感兴趣的点采用更小的单元进行网格划分。

1.2.2 加载求解

在ANSYS Workbench中将塑料平开门门框的四周加固定约束，并将塑料平开门所受风载荷均匀加载到门扇上，对模型进行求解。

假设该平开门安装在济南市区高度50 m处，根据GB 50009—2012《建筑结构荷载规范》规定的风荷载计算方法，计算出该平开门所受风载荷标准值为：Wk=1.07 kN/m2。

2 模拟结果分析

对上述模型进行求解。为便于观察，获得更好的视觉效果，在模拟过程中将门扇的玻璃隐藏。图5、图6分别为1个和2个锁闭点锁闭器的变形模拟云图。

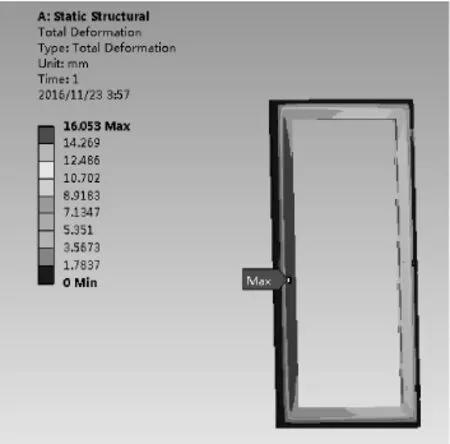
图5 1个锁闭点门框变形模拟云图

从图5可以看出，该平开门安装1个锁闭点锁闭器时，门框的最大变形出现在框的中部，最大变形量为16.053 mm，且最大变形量分布范围广，基本上覆盖整个边框。

当平开门安装2个锁闭点锁闭器，锁闭点分别分布在图3中①、②、③、④、⑤5个不同位置时，在风荷载作用下门框的最大变形量如表1所示。

表1 2个锁闭点分布在不同位置时风荷载作用下门的最大变形量

图6 2个锁闭点时变形模拟云图

由表1可以看出，当锁闭点分布在图3中的位置④时，风荷载作用下门框的变形量最小，变形量为7.9844 mm，但此时最大变形量分布范围广，整个门边框处的变形量几乎都接近最大值。当锁闭点分布在图3中的位置①、②、④、⑤处时，门的最大变形量差别不大，但在①、②处时最大变形量分布范围小，①、②处约位于距离门上部和下部1/6处。

综合考虑，建议当平开门窗选用2个锁闭点锁闭器时，2个锁闭点安装位置可以在距离门窗上下部约1/6处，这样既可保证门窗变形量相对较小，同时又能很好地保证变形的均匀性，从而也可以很好地保证门窗密封、保温等性能。

3个锁闭点锁闭器的模拟结果如图7所示。

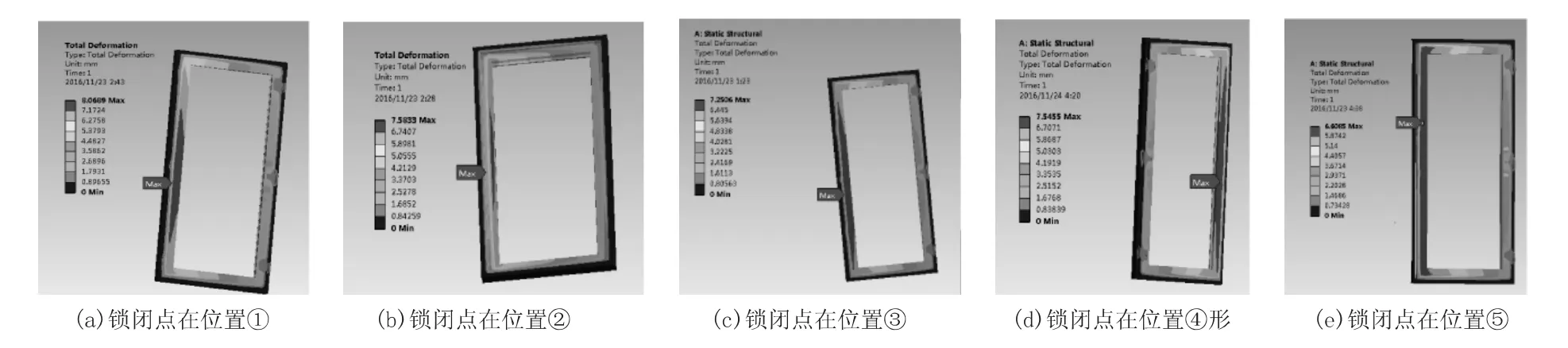
图7 3个锁闭点时的变形模拟云图

当平开门安装3个锁闭点锁闭器，锁闭点分别分布在图4中①、②、③、④、⑤5个不同位置时，在风荷载作用下门框的最大变形量如表2所示。

表2 3个锁闭点分布在不同位置时风荷载作用下门的最大变形量

由表2可以看出，当锁闭点分布在图3中的位置⑤时，门框的最大变形量最小，变形量为6.6085 mm，此时，3个锁闭点分布距离最近，接近门中间位置。从图6（a）变形云图中也可以看出，锁闭点分布在图3中的位置⑤时，门的最大变形量虽然最小，但最大变形量的分布范围最广，整个门边框处的变形量都接近最大值；当锁闭点分布在图3中的位置①、②、③、④处时，门的最大变形量差别不大，但在位置①、②处时最大变形量分布范围相对较小，①、②处约位于距离门上部和下部1/6处。

综合考虑，建议当平开门窗选用3个锁闭点锁闭器时，3个锁闭点可以按照以下方案布置：中间锁闭点安装在门窗边框中部，边上2个锁闭点安装位置①～位置②处，即约位于距离门上部和下部1/6处。

图8为5个锁闭点锁闭器的模拟结果。

图8 5个锁闭点时的模拟结果

由图8可以看出，2种情况下，平开门最大变形量差异很小，分布范围也基本相同，由此可以建议，当平开门窗选用5个锁闭点锁闭器时，5个锁闭点可以按照以下方案布置：边框中间锁闭点、上下框处锁闭点分别分布在门窗框中部，边框两端的两个锁闭点分布在位置①～位置②处，即约位于距离门上部和下部1/6处。

根据上述模拟结果，对锁闭器锁闭点数量不同时门的最大变形量进行汇总（选取不同位置时的最小值作为代表值），如表3所示。

表3 锁闭点数量不同时风荷载作用下门框的最大变形量

由表3可以看出，锁闭器锁闭点的数量从1到5个递增时，门的变形量从大到小递减，而且变化明显。因此选择多锁闭点锁闭器对减少风荷载作用下平开门窗的变形量效果显著。并且多点锁闭会使门窗受力均匀，使门窗框扇之间的密封胶条均匀产生弹性变形，从而可以大大提高门窗的密封性能和保温性能。

3 结语

通过对锁闭器锁闭点配置数量和分布位置不同情况的模拟分析发现，平开门窗锁闭器锁闭点的数量越多，在风载荷作用下门窗的变形量越小；平开门窗锁闭器锁闭点的位置分布越均匀，在风载荷作用下门窗变形量越小。在门窗设计制作过程中，可以根据门窗扇尺寸大小以及价格等因素，合理确定锁闭器锁闭点的数量，并将锁闭点进行合理分布。

在门窗五金件设计、使用中，锁闭器作为门窗的核心部件，具有重要的地位。由于门窗在使用过程中的变形会直接影响门窗的正常使用，以及门窗的密封性能和保温性能，利用ANSYS Workbench对锁闭器对平开门窗的变形性能影响问题进行模拟分析，对于门窗变形性能的研究是非常有意义的。