分层抽样设计中的样本量最优分配问题探究

陈 璟

（浙江省杭州第二中学 浙江 杭州 310051）

1 研究背景

调研是人们为了了解某种现象或达到某种目的，有计划地搜集社会上的相关信息并进行描述、分析和提出解决方案的过程。譬如在我们的校园生活中，老师和同学就常需要展开社会调研活动，如调查高三学生的平均学习时间、中小学生的网络购物观念等等。其中，调研中最重要的环节就是抽样问题。分层抽样，以其精度、费用等方面的优势，成为众多抽样方法中最常用一种。但在分层抽样中，该以什么比例抽样才能保障一定的精度和控制一定的成本是调查人员所需要考虑的问题。因此，本文将对其的抽样方式进行详细探究，重点考虑分层抽样的样本量分配问题。

本文将关于分层抽样的记号定义如下：

设总体分为L层，以h 表示层的编号，h=1，2，…，L。

N表示总体单元数，n表示样本单元数。

第h层的单元总数为Nh，满足

抽样比f=n/N，第h层的抽样比fh=nh/Nh。

第h层总体层权Wh=Nh/N，样本层权wh=nhn。

2 分层随机抽样

在实际问题中，大多数情况下我们的总体目标量是总体均值，总量和比例。其中，总量和比例都可以看成是均值的简单变化。因此，本文将重点讨论跟总体均值相关的估计量的性质。为了探究不同方法的估计效果，这里我们首先给出一个案例。

某工厂生产的机器供应全国2300家用户，想请用户对该厂机器进行评分。现在把这些用户分为本地区、本省外地区以及外省三层，每层中相关资料如表1所示(其中ch为在第h层中的单位成本费用)。

表1 案例数据说明表

我们的目标是设计分层抽样方案来估计用户对机器的平均评分。对此，我们提出如下问题：a.如何抽样操作最简便；b.如何得到精度最高的估计量；c.怎样设计抽样方案使得成本最低。

2.1 简单随机抽样

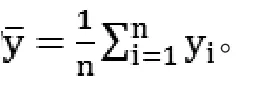
由于-y是无偏估计，因此其精度可用方差衡量，方差越小，精度越低。利用性质2，我们可得到样本量n和方差V0之间的关系为。在工厂案例中，S2未知，但可由=2.73得到。表2展示了样本量n和方差V0间的关系。可以看到，当样本量从10上升到100时，均值估计的方差下降非常迅速；而当样本量进一步扩大时，方差的下降速度变慢。

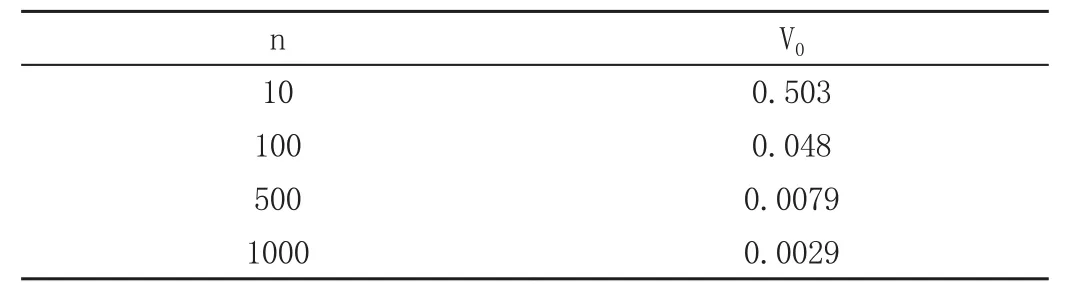
表2 简单随机抽样下n和V0的关系

2.2 分层随机抽样

在一些情况下，简单随机抽样常常不便于抽样工作的组织。而分层抽样将调研对象按某种属性（如地域、性别、类型等）划分成不同的层，再对层内总体进行抽样往往在实际中有着重要应用。如果对每一层的层内都采取简单随机抽样，就是分层随机抽样。在分层随机抽样下，我们对总体均值的样本估计有如下性质

性质1：总体均值Y-的无偏估计为

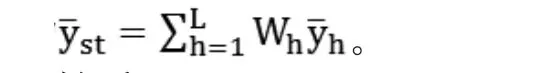
性质2：

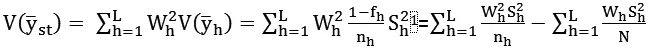
由于在分层抽样中，我们是按照单元的属性进行分层，层内单元相似而层间单元相异。同时，从上述性质可以发现，在分层随机抽样下，估计量的方差仅和层内方差有关、和层间方差无关。因此，分层抽样的估计精度一般较高。而如何确定总体样本量n和每一层的样本量nh又是分层抽样的关键。

3 分层抽样下的样本分配

实际生活中的抽样工作会受多个因素限制，例如成本等等，都会影响到样本量的选取。同时，我们收集到的问卷或者信息可能是无回答或者不完整的。因此，本文主要考虑了成本和回答率对样本分配的影响。

回答率：设每层的回答率为kh，则每层实际需抽的样本为。

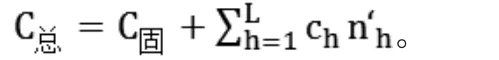
3.1 按层权分配样本的比例分配

分层抽样最直接的方法就是按照每层的层权Wh来分配样本。即，样本量的分配比例wh=nh/n与各层单位数占总体单位数的比例Wh=Nh/N一致，每一层的抽样比fh=nh/Nh等于总体的抽样比f=n/N。当我们确定总样本量n，即可得到第h层的样本量nh=nWh。

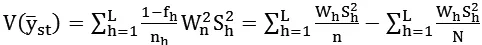
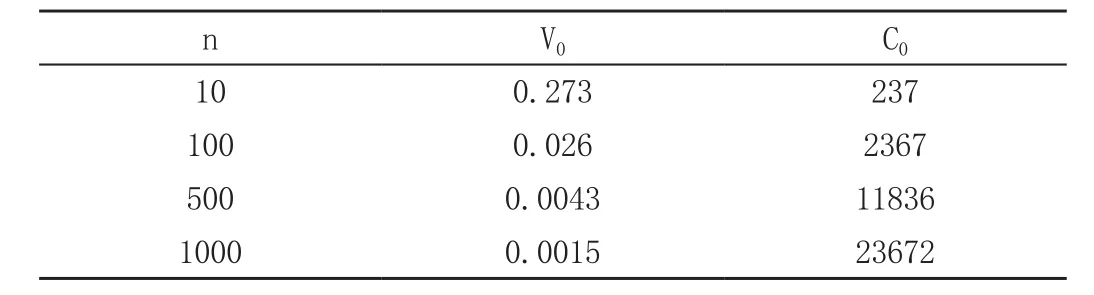
表3 比例抽样下样本量、方差和成本关系表

3.2 精度确定，成本最小的最优分配

尽管比例抽样操作简便，但没有考虑每一层的单位成本。所以，在这一部分我们将探讨如何在保证估计有效的情况下使得费用最小的样本分配方案。

由分层抽样的性质2，我们要在希望的精度下，找到nh使得所花费的总费用最小。即，

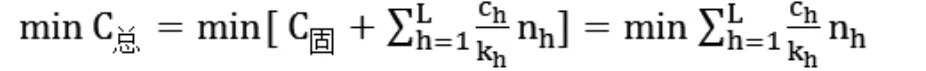
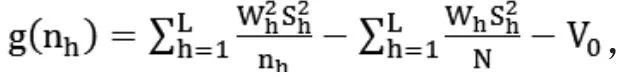
化简整理后，解得第h层的样本层权为

这个解就是考虑每层回答率和单位成本，当确定估计精度下使得总成本最少的样本分配方案。而在精度V(yst)=V0时，我们可知总样本量n为

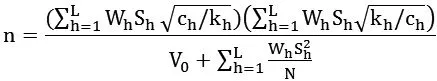
事实上，当我们用拉格朗日乘子法求出“成本固定，精度最优”时的样本分配w’h时，会发现w’h=wh。所以，按照上述比例分配样本，是能够同时满足“精度固定，成本最少”和“成本固定，精度最优”的最优分配方案。

根据如上的最优分配方案对案例中的三个层级分配样本，可得到表4。这里我们控制均值估计的精度V0和比例估计的4个值一致，并分别基于上述公式算出总样本量n和变化成本C0。可以看到，当精度相同时，最优分配相对于比例分配需要更多的样本，尤其是当需要的精度很高时。但是成本却比比例分配要少。

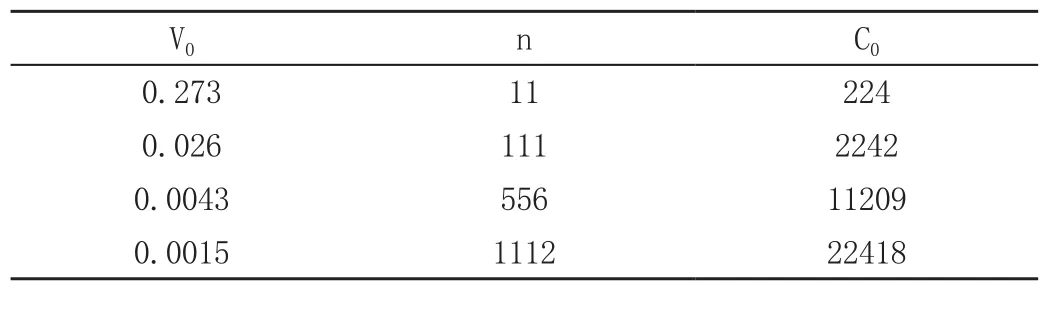
表4 最优分配下方差、样本和成本间关系表

3.3 内曼分配

若根据内曼分配来分配案例中的样本，可得表5。可以看到，当精度一致时，内曼分配所需样本数要少于比例分布和最优分配。这说明内曼分配在这几种方法中估计精度最高。但是成本C0也明显高于其他两种样本分配方法。这是由于在本例中，各层的单位成本不同。如果实际情况中的各层单位成本相同，那么内曼分配和最优分配的结果将完全一直。

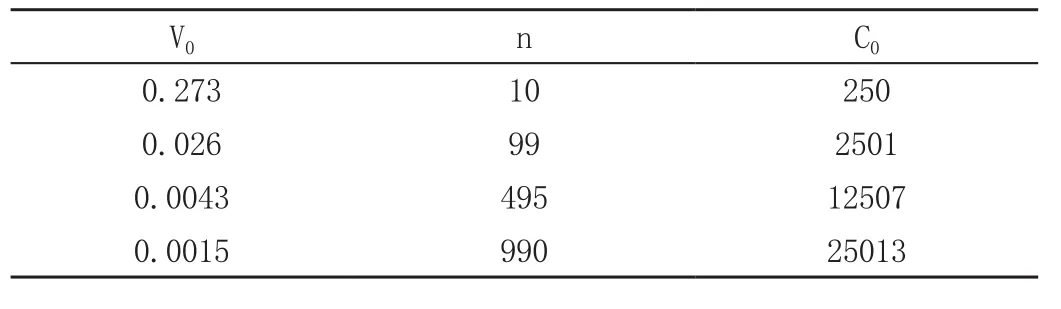
表5 内曼分配下精度、样本量和成本间关系表

4 讨论

本文重点讨论了分层抽样中的样本分配问题。希望能为广大中小学生在社会调研中选择抽样方法上提供理论依据。通过一个案例，我们讨论了不同分配方法的性质和估计效果，主要结论如下：

方差随着样本量的增加而减小，但减小的速度逐渐放慢；

分层随机抽样精度比简单随机抽样精度高；

比例分配操作简便，但估计精度不如内曼分配，成本控制效果不如最优分配；

当各层单位成本相同，最优分配就是内曼分配，且达到精度最高，成本最低的效果。

[1]王晓燕，刘建平.分层抽样样本量最优分配问题新探[J].统计与决策，2004(6)：17-18.

[2]金勇进，杜子芳，蒋妍.抽样技术[M].中国人民大学出版社，2012.