仿生学气动噪声控制研究的历史、现状和进展
2018-03-09乔渭阳陈伟杰王勋年陈正武西北工业大学动力与能源学院陕西西安709中国空气动力研究与发展中心空气动力学国家重点实验室四川绵阳6000中国空气动力研究与发展中心气动噪声控制重点实验室四川绵阳6000
乔渭阳, 仝 帆, 陈伟杰, 王勋年, 陈正武(. 西北工业大学 动力与能源学院, 陕西 西安 709; . 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 6000;. 中国空气动力研究与发展中心 气动噪声控制重点实验室, 四川 绵阳 6000)
0 引 言
随着民用航空的快速发展,飞机噪声问题已成为目前航空界普遍关心的问题之一。面对未来迅速发展的航空运输市场,特别是面对未来人类对环境保护要求的不断提高,飞机适航噪声标准进一步严格,对大型客机及其发动机的气动噪声控制,已成为目前影响飞机研制与适航取证的关键技术之一[1]。因此,国内外众多航空研究机构都将气动噪声控制列为未来航空技术发展的重要方向,投入巨大的研究力量,为使其飞机能满足未来更严格的噪声适航标准和市场竞争而进行新的努力。NASA根据美国NextGen计划将亚声速固定翼民用飞机发展计划分为N+1、N+2、N+3代,并分别制定了它们相应的评价指标,对噪声的要求是相比于第4阶段分别降低32、42、71 dB。欧洲也制订了类似的降噪计划,到2020年新飞机必须满足CO2、噪声和油耗各降低50%, NOx减少80%的环境目标[2]。可见未来民机面临着巨大的降噪要求挑战。
然而,与巨大的降噪要求相矛盾的是,目前飞机降噪技术进步的趋势趋于缓慢[1],传统的飞机气动噪声控制技术越来越困难。这是由于一方面随着发动机降噪技术的不断进步,发动机内部已经没有一个明显大的噪声源,同时发动机的噪声与飞机机体噪声相接近,这时飞机降噪必须进行很多个噪声源的同时降噪。另一方面,目前对于容易控制的单音噪声源已经有了有效的控制措施,湍流宽频噪声重要性逐渐凸显出来,由于湍流宽频噪声源机理复杂,噪声辐射与湍流、非定常流等复杂流体力学问题相互交织、互相影响,使得对湍流宽频噪声的控制非常困难。目前还严重缺乏针对湍流宽频噪声的有效控制方法。因此,不断探索和发展具有创新性的湍流宽频噪声的降噪设计理论,成为当前气动声学理论的重要发展方向[3-4]。
近年来,基于仿生学原理的降噪设计概念的出现,为降低飞机/发动机湍流宽频噪声提供了新的研究思路,获得了当代气动声学领域广泛的重视和发展。
在自然界中,许多动物已经经过了几百万年以至上千万年的生存竞争和进化,为了生存的需要,许多飞行类动物和鱼类形成了一些特殊的、超群的飞行/游动本领,这些特殊的飞行/游动本领包含着丰富多彩的对流动的控制原理。例如,大多数鸟类,包括白天活动的猫头鹰,飞行时羽毛拍打空气都会发出嗖嗖的声响,而夜行猫头鹰是一个例外,它的翅膀和羽毛有消声作用,飞起来悄无声息,显得神秘莫测。这类猫头鹰在白天、黑夜特别是在黄昏时从3~6 m高度的栖息处急速地俯冲向猎物,能够保持身体的平衡并且不发出任何可能导致猎物逃跑的声响(也称为寂静飞行)。通过对动物界中这一特殊寂静飞行本领进行深入细致的观察,研究其基本原理,并把这些原理应用到低噪声飞行器/发动机设计中去,就构成了气动声学领域特有的仿生学降噪研究方向。
自发现猫头鹰静音飞行本领和座头鲸超常的机动能力以来,人们在理论、实验与数值模拟方面开展了大量的研究以期望将动物的这些超常本领用于低噪声飞行器设计。
20世纪90年代,Howe首次公开发表了模仿猫头鹰翅膀的锯齿尾缘翼型降噪的理论分析研究结果[5-6],并给出了锯齿尾缘降噪的预测模型。在Howe的理论研究后,众多研究证实了锯齿尾缘的降噪效果。Dassen[7]、Braun[8]、Oerlemans[9]等在风力机上初步证实了尾缘锯齿的降噪效果。2010年后,针对尾缘锯齿人们做了大量的工作。如Gruber[10-14]、Chong[15-20]与Moreau[21,22]等针对NACA65、NACA0012翼型及平板开展了大量的尾缘锯齿降噪实验研究。Arina[23]与Jones[24-25]分别采用大涡模拟(LES)与直接数值模拟(DNS)研究了尾缘锯齿的降噪效果与降噪机理。此外,Finez[26]、Weckmüller[27]与Jaron[28]等还研究了尾缘锯齿对压气机叶栅与开式转子的降噪效果。Vathylakis[29]、Leon[30-31]、Avallone[32]等对尾缘锯齿结构的流场进行了详细测量。理论方面,最近Lyu[33]还提出了新的尾缘锯齿降噪模型。国内的黄迅[34]也提出一个锯齿平板对声波的散射模型。关于仿生学尾缘锯齿降噪,国内的吉林大学[35-36]、西北工业大学[37-45]、西安交通大学[46-47]、清华大学[48]、北京航空航天大学[49]、上海交通大学[50-51]等也开展了大量的研究。最近,Avallone[52]、Clark[53-54]等还提出了新型的尾缘锯齿结构和仿生学尾缘结构。
此外,模仿座头鲸鳍肢前缘凸起结构的波浪状前缘结构也得到了人们的关注。Fish首次发表了座头鲸鳍肢前缘凸起结构的流体动力学性能研究[55]。之后,大量研究者开展了波浪状前缘结构对翼型气动性能影响的研究[56-71]。Hansen[72]首次研究了波浪状前缘对翼型单音噪声的控制效果。Polacsek[73]、Gruber[74]、Clair[75]、Narayanan[76-77]、Chaitanya[78]等针对波浪状前缘降低湍流宽频噪声的效果开展了大量的实验研究。Clair[75]、Haeri[79]、Turner[80]、Kim[81]、Aguilera[82]等数值模拟研究了波浪状前缘的降噪效果与降噪机理。理论方面,Mathews[83]、Lyu[84]等提出了波浪/锯齿状前缘降低平板噪声的理论模型。国内方面,西北工业大学也开展了大量的波浪状前缘降噪的实验与数值模拟工作[85]。最近,Chaitanya[78]等还提出了新型的仿生学叶片前缘结构。
近年来针对仿生学降噪国内外开展了大量的研究,并且不断提出新型的仿生学降噪思路,推动仿生学降噪成为一个快速发展的方向。笔者对近年来的仿生学降噪工作进行了系统的梳理,回顾了仿生学气动噪声控制技术的研究历史,并详细介绍了机翼/叶片尾缘和前缘的仿生学降噪研究现状和发展动态,分析了目前仿生学气动噪声控制理论和技术的主要问题及未来的研究重点和发展方向。
1 仿生学气动噪声控制研究的历史回顾
“仿生学”概念于1960年首先由美国Steele等提出,“师法自然”是仿生学的核心,人类社会文明的起源源于人类非凡的智慧,而人类的智慧体现为学习、创新与创造,向自然学习无疑成为推动人类文明进程的重要方式,人类在学习、模仿、改造自然中不断前进,催生了生机勃勃的现代文明。“仿生学”本质上就是模仿生物的特殊本领的一门科学。“仿生学” 籍了解和研究生物的结构和功能原理,为工程技术提供新的设计思想及工作原理,并通过“仿生学”原理,研制新的机械和新技术,或解决技术上的难题。而仿生学流动控制和气动噪声控制仅仅是“仿生学”领域中非常细小的一个学科分支,它属于“力学仿生”中的一个研究方向。
1.1 寂静飞行鸟类生物学结构观察研究的回顾
尽管“仿生学”作为一门学科在20世纪60年代被确认,但是仿生学流动控制和气动噪声控制却早在20世纪初就得到人类的关注和研究。
早在1904年,德国科学家Mascha就研究了鸟类翅膀和羽毛的生态学特征[86],他首次注意到了夜行猫头鹰翅膀和羽毛的特殊性,观察到夜行猫头鹰翅膀中向上弯曲羽支形成的梳状结构和很长末梢羽小支(如图1所示),并认为这是其寂静飞行的根源。1934年,英国科学家Graham第一次全面研究了猫头鹰寂静飞行的原理[87],他仔细比较了具有寂静飞行本领的猫头鹰和不具备寂静飞行本领的老鹰的翅膀和羽毛,通过全面分析比较,他总结出具有寂静飞行本领的猫头鹰的翅膀和羽毛具有如下三个特征:1)猫头鹰翅膀上的特殊的初级羽毛呈锯齿状排列,构成翅膀前缘梳状结构,像一把梳子(如图1右下角所示);2)在翅膀后端上的特殊曳尾羽毛排列得像一条围巾的须边,构成翅膀尾缘的流苏结构(如图1右上角所示);3)猫头鹰翅膀上的其它部分和腿部都被厚实柔软的绒羽覆盖着。Graham认为上述3个独特的生态学特征,是猫头鹰能够寂静飞行的原因。但是,Graham并没有实验证实这些特殊生态学特征的降噪能力。1962年,Thorpe和Griffin等第一次真正进行了猫头鹰飞行时的噪声辐射特性实验测量分析[88],他们的实验使得人们首次认识到了在拍打飞行中夜行猫头鹰与其他飞鸟噪声辐射的区别。到了20世纪70年代,Kroeger等首次全面地研究了猫头鹰低噪声飞行特征并探讨了在低噪声飞机设计中的工程实现性,这项工作获得的许多结果,成为后来进行低噪声机翼/叶片设计的重要基础[89-90]。为精确测量猫头鹰飞行中的声学特性,Kroeger等在一个专门的实验大厅对猫头鹰飞行噪声进行测量,他们让经过训练的“大林鸮”从距离地面3 m高的栖息处向前下方食物放置处飞去,然后测量了大林鸮的飞行路线、飞行速度及其不同飞行高度时的噪声大小。这项重要的实验工作,首次证实了Graham对猫头鹰低噪声翅膀与低噪声结构的分析,他们的实验发现,当剪去猫头鹰翅膀前缘梳状结构的初级羽毛和尾缘流苏结构的曳尾羽毛,则大林鸮的飞行噪声就像与其重量和大小相同的其他类型飞鸟一样强烈,而且会影响其飞行稳定性,这时大林鸮已经不能沿着直线从栖息处飞向食物,毫无疑问,如果不是上述羽毛和翅膀的特殊结构,猫头鹰是无法获取猎物和生存的。但是,由于实验条件的限制,Kroeger等的实验只能在很短的飞行距离下测量猫头鹰的噪声,无法模拟猫头鹰在自然飞行状态下的特性,而且,他们的实验也没有与其他飞鸟噪声辐射进行比较。德国科学家Neuhaus等实验对比分析了黄褐鹰与绿头鸭的飞行噪声特性[91],他们在大型室内体育馆分别对保留和剪去翅膀前缘梳状结构后的黄褐鹰的飞行噪声特性进行了测量,在室外湖边则测量了绿头鸭的飞行噪声。 Neuhaus等通过与飞行速度、飞鸟重量的关联分析计算,发现在最大噪声幅值,绿头鸭的噪声辐射功率是猫头鹰的30倍,而在整个频率范围内比较,绿头鸭的噪声辐射功率是猫头鹰的200倍。Neuhaus等的实验进一步证实猫头鹰确实比其他鸟类飞行噪声低很多。

图1 猫头鹰翅膀的特征Fig.1 Characteristics of owl wing
随着实验测试技术的不断发展,近年来对猫头鹰低噪声辐射特性的实验测量分析更加深入细致。2009年德国科学家Geyer等在声学风洞实验测量了食雀鹰和黄褐鹰翅膀的噪声辐射特性[92]。而为了实验测量完全真实飞行状态下猫头鹰噪声辐射特性,最近(2011年),德国勃兰登堡工业大学的Sarradj等[93]采用传声器阵列技术和双通道录像技术,在野外对自由飞行状态下茶隼、哈里斯鹰、仓鹰等种类的飞鸟的噪声特性进行了实验,50多个飞行实验结果进一步证实,即便是飞行速度相同,猫头鹰的飞行噪声也要比其他鸟类低几个分贝,特别是在频率1.6 kHz以上范围,猫头鹰飞行的噪声非常低,猫头鹰捕食猎物的听觉最敏感范围为2~20 kHz,而猫头鹰滑行或拍打翅膀产生的噪声大多处于2 kHz以下,猫头鹰在2 kHz以上产生的噪声很小,对于猎物来讲,猫头鹰的飞行几乎是“寂静”的。

A/F:前缘; B/G: 尾缘;C/H: 绒毛; D/I: 孔隙度对比;E/J: 绒羽倒钩图2 猫头鹰与鸽子翅膀羽毛的对比(上:猫头鹰,下:鸽子)[94]Fig.2 Comparison of wing feathers between owl and pigeon[94] (up: owl, down: pigeon)
近年来,国内针对飞鸟的声学特殊结构也开展了相关的研究工作。吉林大学的陈坤以及中国科学院的孔德义等对猫头鹰的微观结构也进行了详细的研究[35-36,95]。他们发现雕鸮(猫头鹰的一种)较长的远端羽小枝能够延伸到相邻甚至更远的羽枝,如图3(a)所示。而普通鵟的远端羽小枝一般只延伸到相邻羽枝,如图 3(b)所示。此外,雕鸮羽毛腹面形貌的高度差要高于普通鵟的羽毛,如图 3(c,d)所示。雕鸮羽毛延长的远端羽小枝会覆盖并穿插于其他羽枝之间,形成多层的网格状多孔结构(图3a),多孔结构能有效地吸收高频声,这也与雕鸮能有效地抑制高频声的结果相一致。雕鸮这种似绒毛的柔软表面使气流流过其翅膀表面时变得柔顺,并能够减弱边界层的湍流[35]。

(a) 雕鸮羽毛腹面,(b)普通鵟羽毛腹面,(c)雕鸮羽毛腹面3D图,(d)普通鵟羽毛腹面3D图
图3雕鸮(猫头鹰)与普通鵟羽毛表面的微观结构[35]
Fig.3Themicrostructureoftheowlandthegeneralbuzzardfeathersurface[35]
1.2 飞机仿生学降噪潜力预测分析
1998年,国际著名气动声学专家英国的Lilley教授在法国图卢兹召开的第4届AIAA/CEAS国际气动声学学术会议中,发表了“猫头鹰的静音飞行研究”一文[96]。该文以气动声学基本原理和机翼湍流噪声辐射模型为指导,基于对飞机与猫头鹰的相似性分析,探索了飞行器所能实现的最低噪声水平。尽管该论文并未对仿生学降噪的基本原理进行研究,但是由于Lilley教授在国际气动声学领域巨大的影响力,也由于当时航空声学在基本理论和方法取得巨大成就的情况下进而面临进一步降低飞机噪声的巨大挑战和技术瓶颈,由此Lilley教授的这篇论文在气动声学领域产生了巨大的影响,进入21世纪之后,一直未得到重视的“仿生学气动噪声控制”很快进入了快速发展时期。
Lilley教授假设飞机飞行时具有与展翅飞行的鸟类相似的发声原理,他采用基于Lighthill气动声学理论获得的机翼远场噪声强度预测公式(Brooks和Hodgson公式[97]),并基于对猫头鹰飞行气动力学与机翼绕流气动力学的理论分析,获得了质量在1 kg到400000 kg之间的宽广范围内,类似于飞鸟展翅飞行构型的飞行物(包括飞机、滑翔机、鸟类等),其噪声辐射强度(不包含发动机噪声,仅展翅飞行鸟类及类似构型飞行器)统一的关联式:

(1)
Lilley教授发现,全尺寸的飞行数据与上述简单公式能够大致匹配,并与测量的飞鸟噪声辐射也吻合。Lilley教授认为,上述简单公式尽管是一个十分粗略的外推公式,但是它传递出十分重要的结论。它表明:对于鸟类、滑翔机、飞机来说,尽管它们的几何外形有较大的区别,但是它们的远场噪声都是遵循相似的速度关联定律。
但是,Lilley教授发现,上述研究结论对于具有“寂静”飞行能力的猫头鹰并不适用。反之,当猫头鹰翅膀的前缘及尾缘梳状羽毛切除的话,上述气动声学公式则对其是成立的。
如前所述,具有寂静飞行本领的猫头鹰的翅膀和羽毛具有三个独特的性质。例如,猫头鹰尾缘结构主要是多个分隔的部分或者类似于锯齿形尾缘,这种结构将会明显减少尾缘散射噪声甚至消除散射噪声。此外猫头鹰翅膀前缘的梳状结构减少了通过尾缘的湍流强度,对于猫头鹰翅膀这种特殊尾缘,消除了散射噪声影响之后其噪声与飞行速度关联关系则是速度的6次方。假如猫头鹰飞行速度为6 m/s 时,由于其独特的翅膀构型,其噪声比其他鸟类将会减少18 dB。类似地,对于飞机在马赫数0.3时,这样的构型能够降噪约为5 dB。Kroeger等对猫头鹰噪声的实验测试证实了猫头鹰前缘及尾缘宽频噪声特征[89]。由于空气流过鸟类身体、翅膀、尾巴以及腿部时产生的边界层内的小尺度湍流是其噪声的重要来源,并且由于这些湍流涡团较小,其产生的噪声主要集中在高频。而猫头鹰全身覆盖的厚厚的绒毛使得空气流过时能够减弱边界层气体的湍流,并且体积足够小的羽毛纤维可以吸收掉小湍流涡的能量,因此这种羽毛提供了一个能量耗散的旁路机理,使得其噪声频率范围小于与黏性耗散相关的频率范围,也使得猫头鹰辐射噪声的频谱在2 kHz以上接近截止频率,即在高频段,猫头鹰全身厚厚的羽绒起到了吸声作用。
正是由于以上三个方面独特的特性,且三种结构的组合效应,导致了猫头鹰具备了寂静飞行能力,也使得猫头鹰不会产生能够让猎物感知到的噪声。Kroeger等[89]的实验测试结果证实,对于猎物来说,在距离地面1 m范围之前,猫头鹰的飞行几乎是“寂静的”,这使得猎物并没有足够的反应时间来逃脱。
Lilley教授指出,如果猫头鹰在长期进化过程中形成的噪声抑制本领可以用于当代民用运输飞机着陆阶段的降噪,这一创举将具有非凡的意义。然而,如果我们忽视猫头鹰等生物低噪声飞行背后隐藏的特殊物理机制与科学机理研究,我们将会错失设计未来安静飞行器的黄金机会。
2 机翼/叶片尾缘仿生学降噪研究现状和发展动态
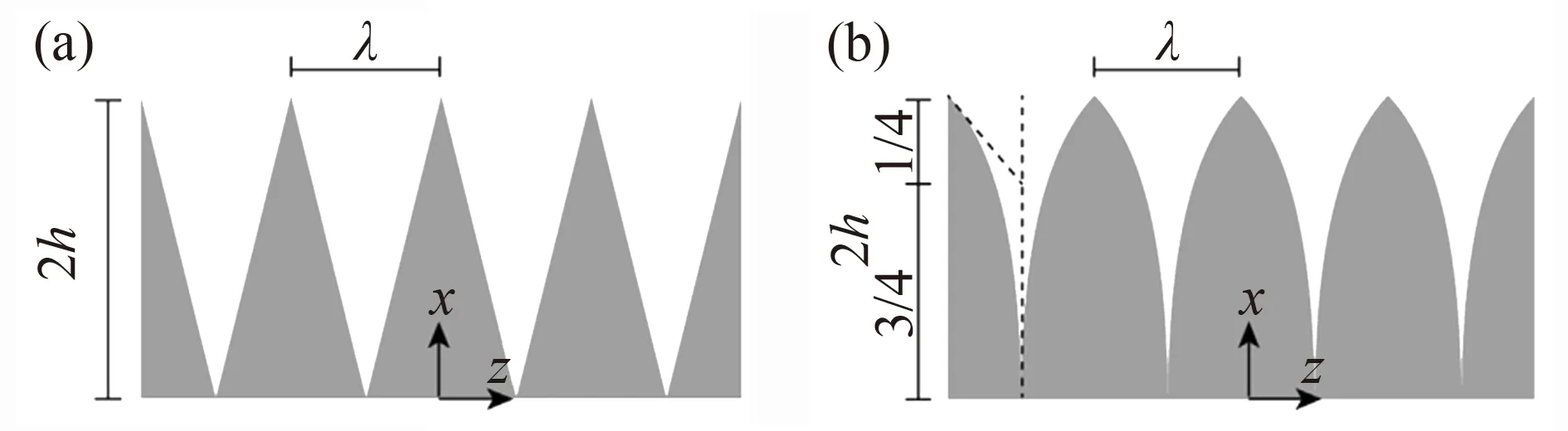
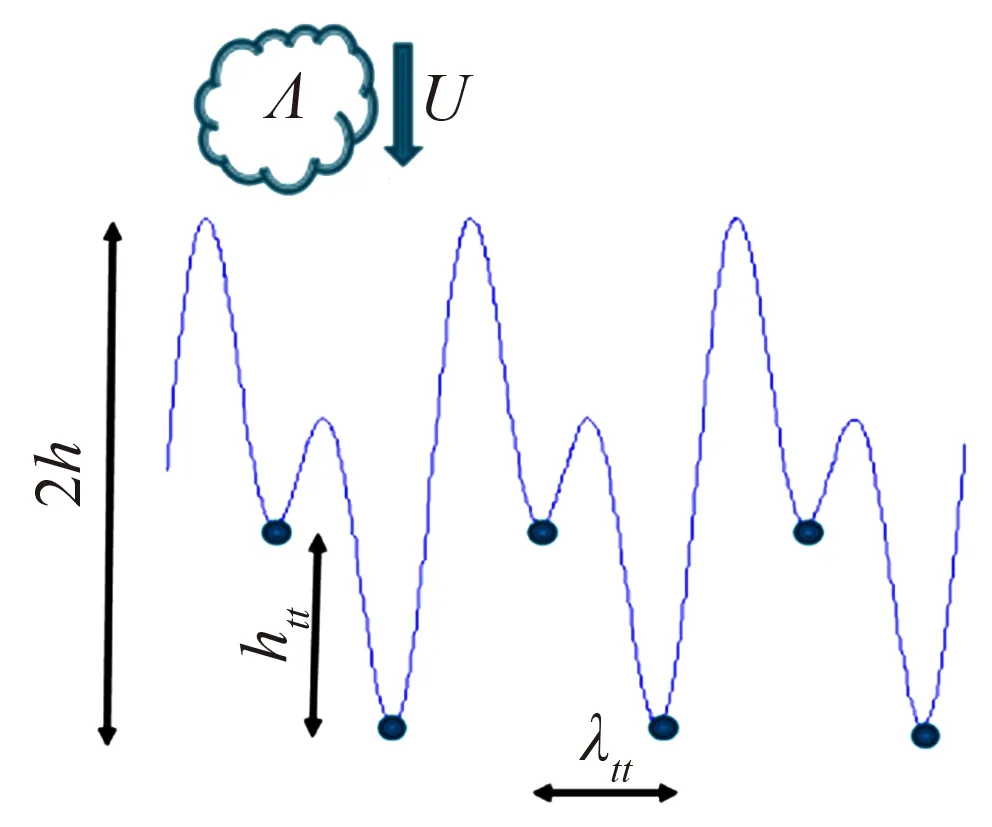
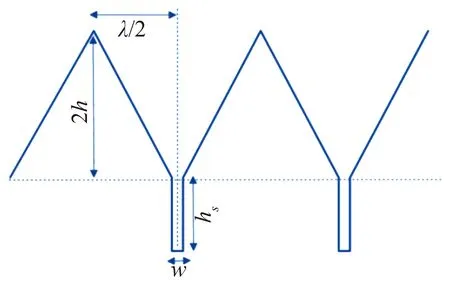
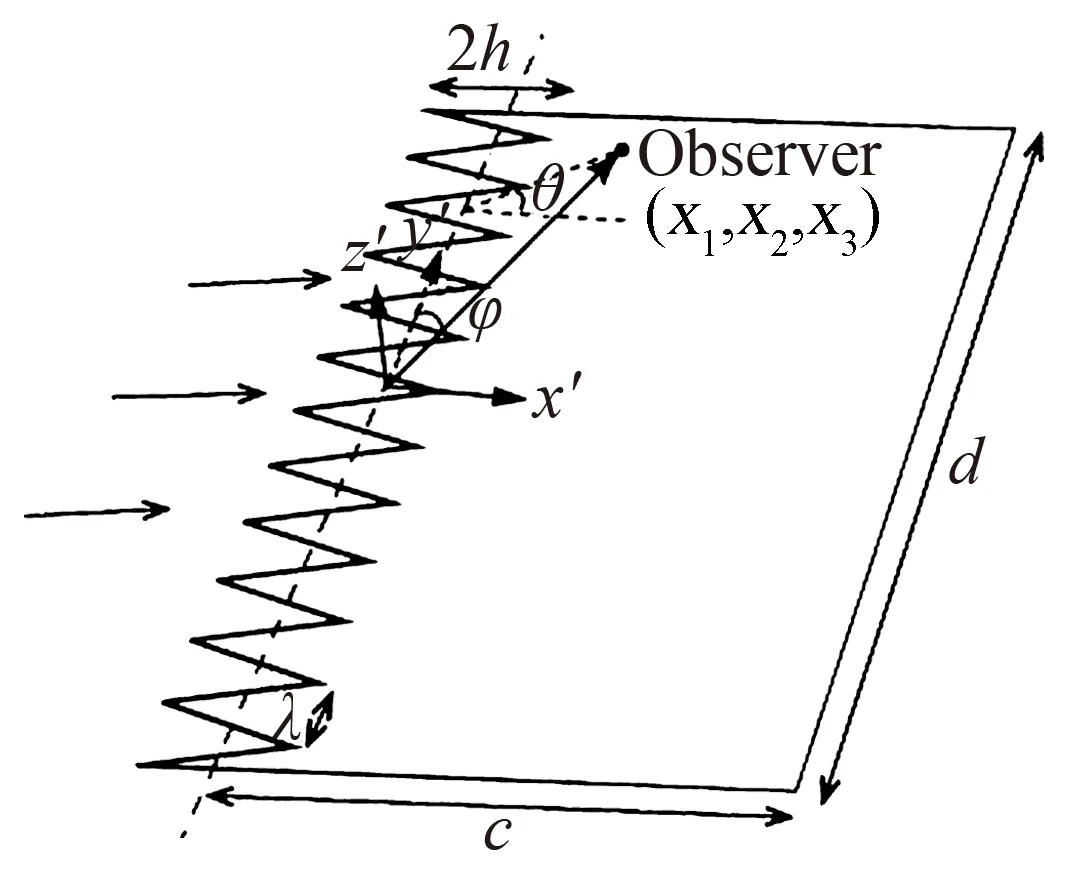
基于对具有寂静飞行能力猫头鹰生态学结构的认识,人们首先提出并发展了仿照猫头鹰翅膀尾缘构型的降噪设计方法。1991年,Howe[5-6]第一次从理论上研究了半无限长平板的锯齿尾缘造型的降噪效果和降噪机理,Howe认为,波数垂直于尾缘的阵风与尾缘干涉辐射噪声的效率高于倾斜阵风的噪声辐射效率,而锯齿形尾缘由于构成了倾斜尾缘结构因此具有降噪能力。基于这种分析,Howe给出了锯齿形尾缘降噪的预测模型(如图4所示),并将锯齿形尾缘的降噪量与锯齿间距λ和锯齿深度2h等参数关联起来。对于锯齿状尾缘,当ωh/U≫1时,降噪效果约为10lg(1+(4h/λ)2)/dB。图5是基于Howe模型的尾缘锯齿降噪效果预测。

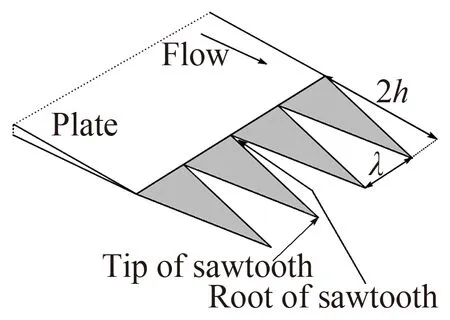
图4 Howe尾缘锯齿理论模型与锯齿参数[6]Fig.4 Theory model of serrated trailing edge of Howe and definition of trailing edge serrations parameters[6]
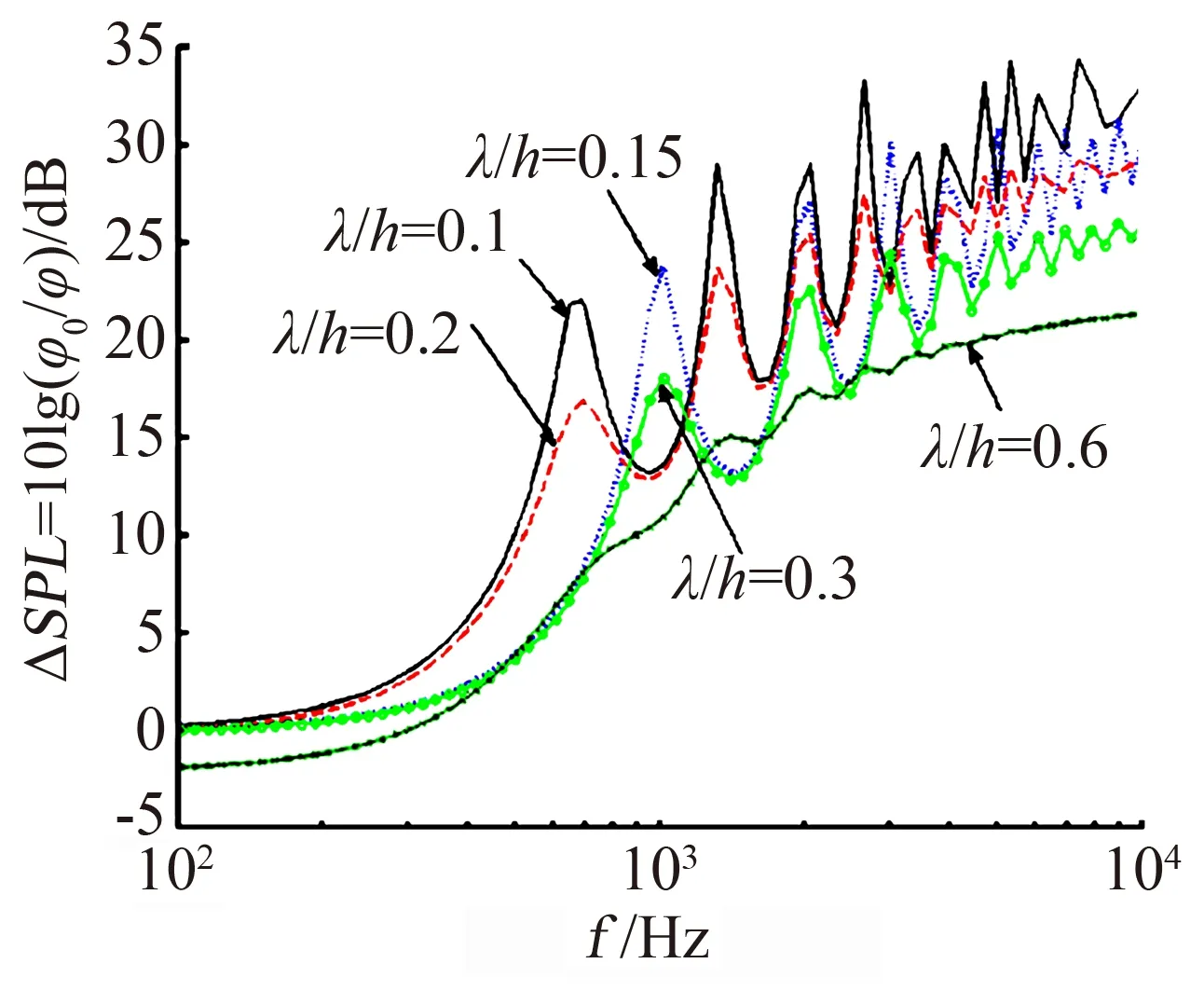
图5 基于Howe模型的降噪效果预测[39] Fig.5 Noise reduction predicted using Howe’s model[39]
在Howe的开创性研究工作之后,许多研究人员采用实验和数值模拟的方法,对锯齿形尾缘降噪的原理和方法展开了深入的研究,众多的研究成果证实了锯齿形尾缘构型降低机翼/叶片尾缘噪声的有效性,其中Dassen[7]、Braun[8]和Oerlemans[9]等的研究成果证实了锯齿形尾缘设计能够有效降低风力机叶片的尾缘噪声(图6),对总声压级的降噪量可达3 dB左右。


(a) 尾缘锯齿降低翼型噪声的实验 (b) 尾缘锯齿在风力发电机上的应用
图6锯齿形尾缘降噪的实验研究及应用[10]
Fig.6Experimentalstudyoftrailingedgeserrationsandits’application[10]
表1列举了自Howe提出锯齿尾缘降噪理论以来,针对锯齿形尾缘降噪效果和降噪机理的主要研究工作。总结分析可以发现,早期的研究工作大部分主要着眼于锯齿形尾缘的降噪效果,对其降噪机理并未给以太多的关注,针对仿生学降噪机理的研究较为缺乏。近年来,国内外的许多研究者逐渐将研究工作的重点放在仿生学流动控制与降噪机理方面。
下面分别从嵌入式尾缘锯齿降噪研究、切开式尾缘锯齿降噪研究和真实叶片尾缘锯齿降噪研究、尾缘锯齿降噪流动与声学物理机制研究等四个方面,评述过去十多年来仿生学尾缘构型降噪研究工作的进展情况。
2.1 嵌入式尾缘锯齿降噪研究
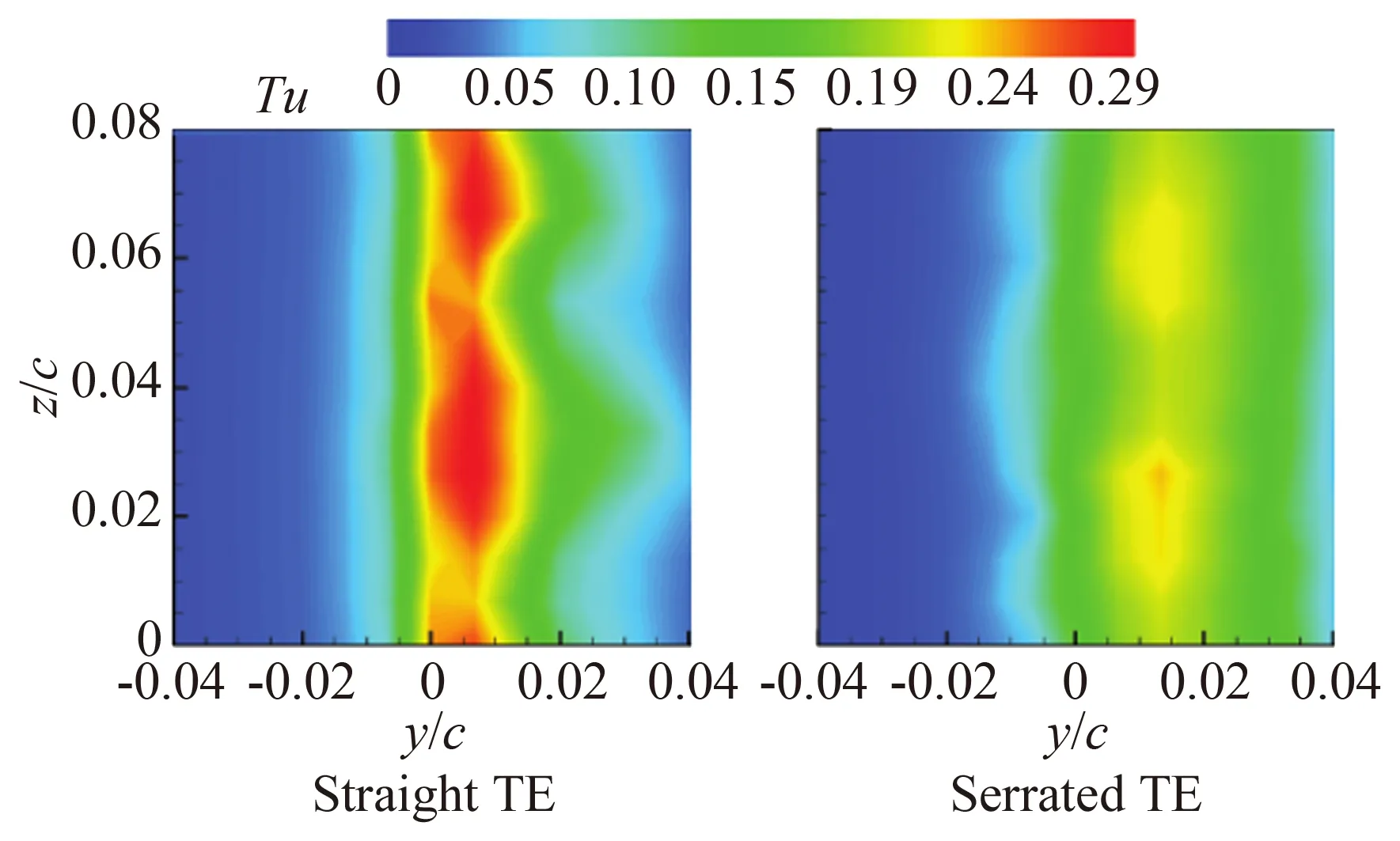
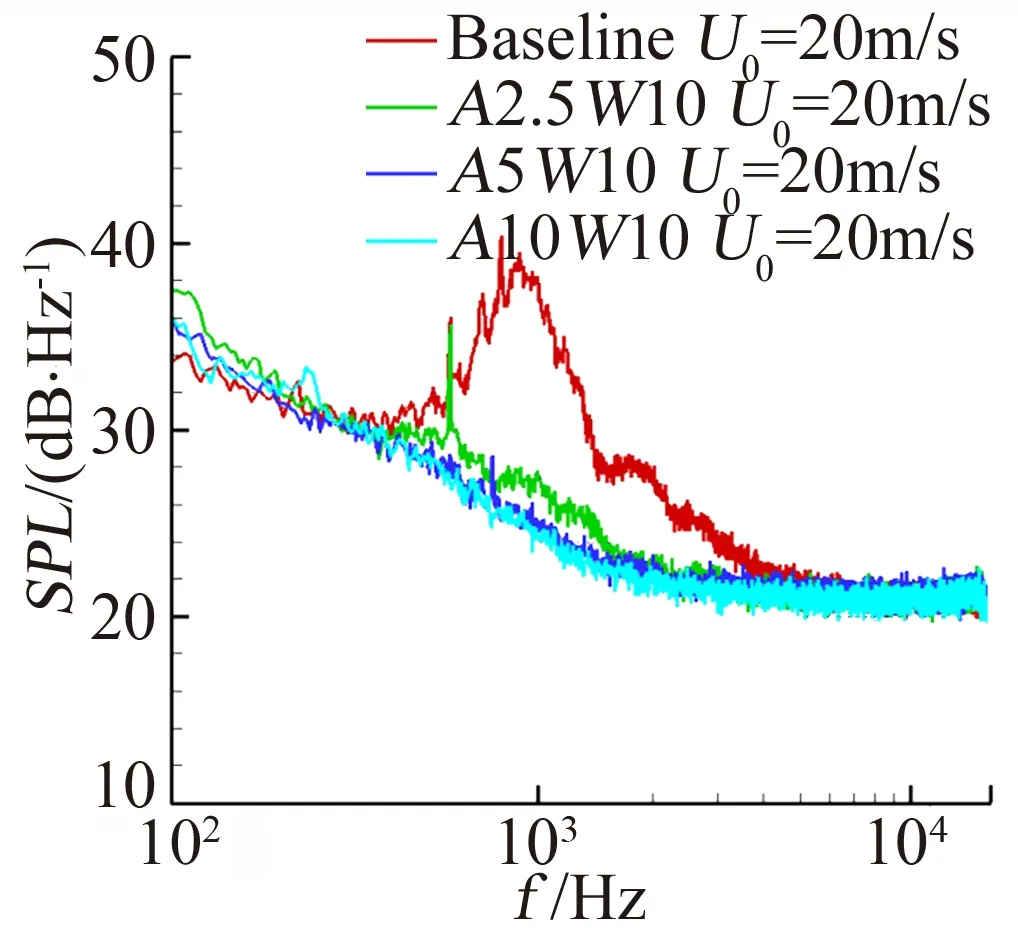
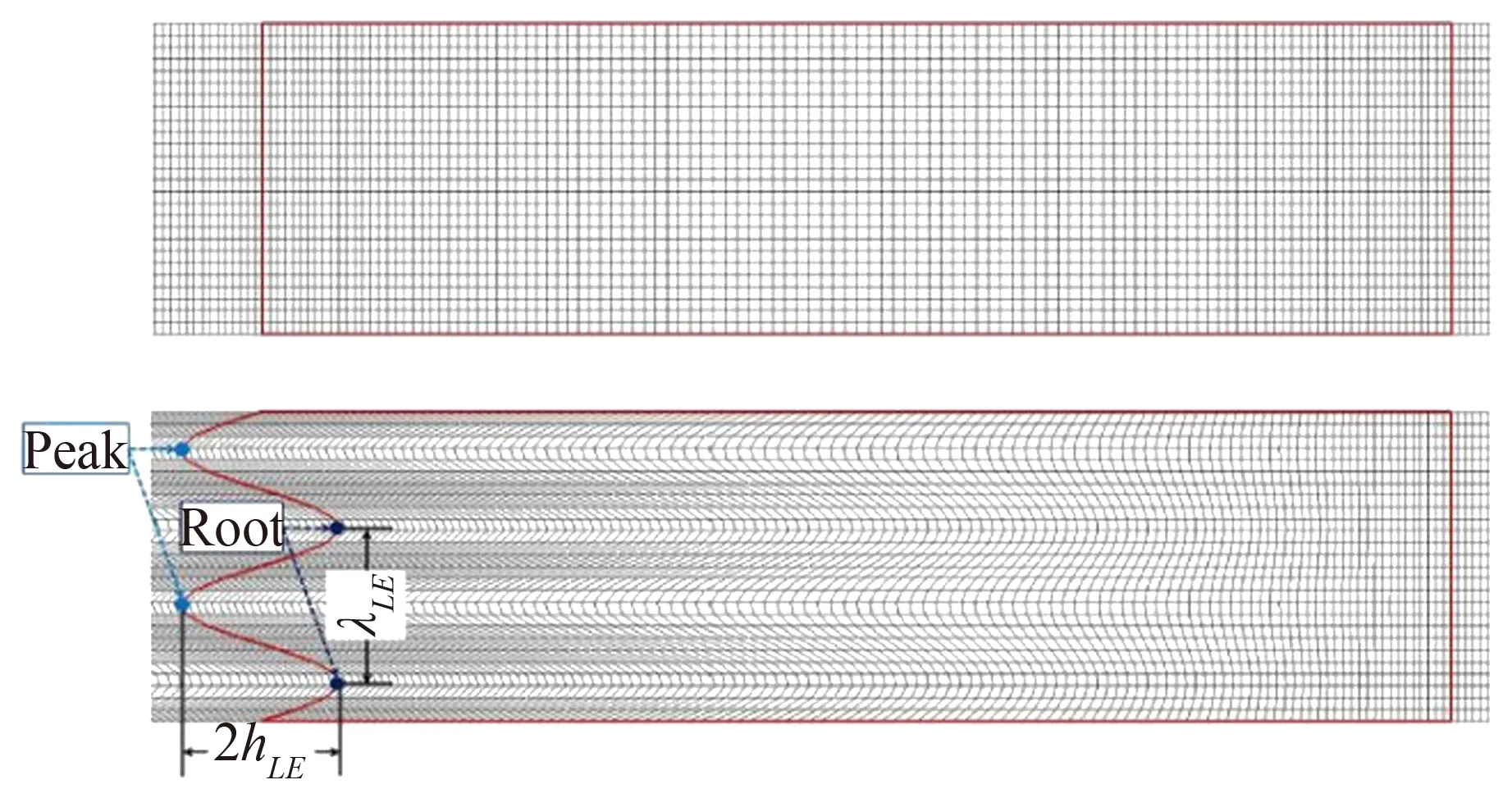
所谓嵌入式的锯齿形尾缘,就是在实际翼型或叶片尾缘,增加一个锯齿形尾缘,并嵌入到原来翼型或叶片,该锯齿尾缘实际上是由一个薄平板构成。而所谓切开式锯齿形尾缘,即通过对基础叶片的直尾缘直接切割,从而构成锯齿形尾缘结构(如图7所示)。

(a) 嵌入式 (b) 切开式
图7锯齿形尾缘[16]
Fig.7Serratedtrailingedges[16]
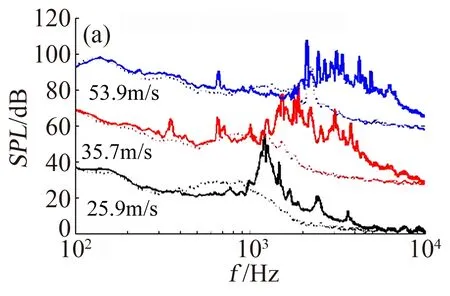
Gruber等[10-14]采用NACA65翼型作为基础叶型,针对嵌入式尾缘锯齿(不破坏叶片原有几何,在直尾缘之后附加锯齿形尾缘结构)的降噪机理进行了大量研究 (如图6a所示),得到了丰富的研究结果。Gruber等[10]首先通过理论和实验方法比较了锯齿形尾缘和开缝式尾缘的降噪效果,结果表明采用这两种结构都能显著降低噪声5 dB左右。此外当频率超过某个临界值时,锯齿形尾缘的降噪效果不再明显,噪声反而有可能增加,这个频率对应fδ/U0≈1(δ为尾缘处的边界层厚度,U0为主流速度)。Gruber等[10-14]设计了多种不同尺寸结构的尾缘锯齿,并实验研究了尾缘锯齿的降噪机理。他们发现: 1) 锯齿形尾缘设计能够有效降低低频范围内的尾缘噪声,同时会增大高频范围内的尾缘噪声,临界频率对应的斯特劳哈尔数约为1。Gruber等认为该现象可能是由于锯齿根部由压力面向吸力面的微射流引起的,如图8所示; 2)锯齿尺寸λ/h越小,即锯齿越尖锐,降噪效果就越好。这与Howe理论的结论相同,然而,研究发现, Howe的理论严重高估了锯齿形尾缘的降噪效果,尤其是在高频范围内;3)当h/δ>0.5时,对于0.01 表1 尾缘锯齿的降噪研究Table 1 Studies on noise reduction using trailing edge serrations (a) 直尾缘 (b)锯齿尾缘 (a) 湍流涡输运速度的对比 (b) 展向相关性的对比 Jones等[24-25]采用DNS的方法对Gruber实验中观察到的降噪现象进行了进一步的研究。数值模拟结果表明,锯齿形尾缘能够有效降低尾缘噪声,最高可达9 dB左右。研究发现,长的锯齿(更尖锐)相比短的锯齿降噪效果要好。此外,Jones指出锯齿形尾缘并未明显改变尾缘上游叶片表面的流动现象(如雷诺应力、湍流谱和展向相干性等),这表明尾缘噪声的降低仅仅是由于声散射过程本身的变化和锯齿区域局部流场的变化引起的。Jones等认为锯齿形尾缘降噪的机理在于锯齿结构产生了大量的马蹄形涡,该马蹄形涡促进了尾迹的混合,从而使尾缘区域的展向相干性降低。 Finez等[26]研究了嵌入式尾缘锯齿在压气机叶栅上的降噪效果(如图10所示),同样得到了可观的降噪量(最大可达5 dB)。在整个频率范围内,锯齿形尾缘的降噪表现和Gruber等的实验结果相似。实验测量结果表明锯齿形尾缘使叶片的阻力增大了14%,锯齿间的微射流现象使叶片尾迹变得更宽,但是速度亏损变小。Finez等给出了三个可能的降噪机理:1) 微射流现象将锯齿吸力面的边界层“抬高”,使得边界层距离叶片表面更远,根据Ffowcs Williams的理论,该现象能够降低固体壁面对各种波的散射效率;2) 锯齿结构降低了由Kutta条件产生的展向脱落涡的展向相干性,根据Howe理论这有助于降低尾缘噪声;3) 根据Howe的锯齿尾缘降噪理论,当尾缘不再与来流方向垂直时,声散射效率会有效降低。 图10 锯齿形尾缘结构降低压气机叶栅噪声的实验[26] Fig.10 Experiment of compressor cascade noise reduction with trailing edge serrations[26] 2012年,Moreau等[21]以平板为对象,研究了中低雷诺数范围下(Re=1.6×105~4.2×105)尾缘锯齿对平板噪声的影响。Moreau对比了长度相同但宽窄不同的两种锯齿结构,一种是2h=30mm、λ=3 mm、λ/h=0.2,另外一种是2h=30 mm、λ=9 mm、λ/h=0.6。Moreau发现锯齿长度相同时,λ较大的宽锯齿对平板的降噪效果更好,如图11所示。 Moreau在后续的工作中用相同的锯齿还研究了更低雷诺数下(Re=1×105~1.3×105)锯齿的降噪效果[22],如图12所示。可以看出,宽锯齿对平板的降噪效果明显好于窄锯齿。同时,Moreau发现窄锯齿在低雷诺数下会产生较强的单音噪声。为了揭示锯齿降噪以及窄锯齿产生额外单音的机理,Moreau测量了平板下游1mm处速度脉动沿展向的分布,见图13。从图13中可看出,尾缘锯齿结构明显改变了尾缘附近的流动,这里正是尾缘噪声的声源区域。对比图12与图13可以发现,湍流脉动在频域内的分布与尾缘噪声的频谱是紧密相关的。可以推测尾缘锯齿是通过改变尾缘附近局部湍流流场而影响尾缘噪声的。对比图13(a)与图13(c)可以看出,对于直尾缘平板,尾缘附近具有强烈的湍流场,湍流脉动非常强烈,而采用宽锯齿后,低频范围内(<1 kHz)湍流脉动强度明显得到降低。宽锯齿可以降低尾缘附近的低频湍流强度,进而降低平板的宽频噪声。对于窄锯齿情况,从图13(b)可以看出在300 Hz与400 Hz附近处有强烈的湍流脉动,而这正好对应图12中的两个单音噪声。与单音噪声频率相一致的这两个强的速度脉动来自于锯齿尖部的涡脱落,窄锯齿会使沿平板展向产生强烈的涡脱落,进而产生强烈的单音噪声。 图11 宽、窄锯齿降噪效果的对比(1/3倍频程)[21] Fig.11 Comparison of noise reduction effects between narrow and wide serrations (1/3 octave)[21] Moreau[21-22]的实验结果表明,宽锯齿能够在整个关心的频率范围内有效降低尾缘噪声,在单音噪声存在时,宽锯齿能够降低总声压级达13 dB。而窄锯齿设计则基本没有降低尾缘噪声,甚至部分结果显示窄锯齿设计显著增大了尾缘噪声。Moreau指出,尾缘锯齿结构显著改变了尾缘区域的流动,这是尾缘噪声降低的主要原因。Moreau认为这甚至比尾缘锯齿对声辐射效率的影响更为重要。在较低的雷诺数下,窄锯齿在齿尖处能够诱发大量的旋涡,这是窄锯齿未能降噪反而增大噪声的原因所在。许影博等[49]的实验结果也表明,较宽的尾缘锯齿降噪效果稍优于窄锯齿,该结果与Gruber等[10]的研究结果不同。 Chong等[15-20]对切开式尾缘锯齿的降噪效果和降噪机理进行了大量的实验研究,与Gruber[10]、Jones[24-25]和Finez[26]等不同,Chong重点研究了尾缘锯齿对单音噪声的抑制效果和抑制机理。他们发现,切开式锯齿形尾缘的降噪效果整体上要优于嵌入式的锯齿形尾缘,并给出了切开式锯齿形尾缘诱发的流向对涡的物理图画(如图14所示)。Chong指出,对于尾缘噪声中不同机制产生的单音噪声,并且锯齿形尾缘都能够进行有效的抑制:1) 尾缘锯齿可以通过微射流现象减弱钝尾缘下游脱落涡的展向相干性,从而抑制由钝尾缘脱落涡产生的单音噪声,并且尾缘锯齿越大,该抑制效果越好;2) 尾缘锯齿能够通过抑制尾缘附近的层流分离泡现象,来减弱层流分离泡对T-S不稳定扰动波的放大效率,从而抑制由不稳定扰动波与尾缘干涉产生的不稳定单音噪声,并且锯齿结构越大,层流分离泡越接近尾缘区域,该抑制效果越好。 (c) wide serration 图13脉动速度谱沿展向的分布(平板下游1mm位置,y=0对应锯齿尖位置,U0=9m/s)[22] 图14 锯齿形尾缘结构产生的流向对涡[17] Fig.14 Counter-rotating vortexes around the serrated trailing edge[17] Chong针对层流翼型不稳定单音噪声进行了专门研究,并研究了尾缘锯齿对于这种不稳定单音噪声的影响[15-20]。在低雷诺数下,当来流是二维流动,湍流度很低时,尾缘噪声会表现出一种独特的窄带特征:噪声频谱会有宽频的凸峰,且此凸峰上会有数个高幅值的单音。与这种噪声特性相对应的翼型边界层主要是层流,而且有可能处于不稳定状态。在某些状态下,流动中的不稳定性(如T-S波)会在边界层中发展、增大,并在尾缘辐射出声,即Brooks提出的机翼自噪声产生的第二种机理。Chong发现尾缘锯齿可以显著降低翼型的不稳定单音噪声。图15是不同尾缘锯齿对不稳定单音噪声的影响[18]。国内陈伟杰等[45]在低湍流度来流情况实验中也观察到类似的现象,实验发现在大迎角状态下,尾缘锯齿可以极大降低翼型不稳定单音噪声,如图16所示。然而,在0°迎角状态下,尾缘锯齿可能会增大翼型噪声。 西北工业大学的仝帆、纪良等[37-44]采用数值模拟与实验的方法研究了尾缘锯齿对SD2030翼型以及涡轮叶栅的降噪效果。研究发现尾缘锯齿可以降低层流边界层分离-涡脱落噪声约16 dB,同时可以降低中低频范围内宽频噪声,高频范围内噪声稍有增大。研究发现,尾缘锯齿可以促进翼型压力面与吸力面气流的混合(如图17所示),抑制尾缘处层流边界层涡脱落现象,显著降低翼型升力脉动。此外,尾缘锯齿可以降低尾缘附近低频湍流脉动强度与翼型表面压力脉动幅值,并改变尾缘附近翼型表面压力脉动的相位。同时,尾缘锯齿也有利于尾缘附近涡量强度的减弱,并能有效降低尾缘处涡的展向相关性,以上几种因素的共同作用使得翼型自噪声降低。此外,清华大学的黄乾[48]数值模拟研究了尾缘锯齿对NACA0018翼型的降噪效果,获得了1.5 dB的降噪量。 (a) S1 (2h=20 mm,λ=4.9 mm) (b) S2(2h=20 mm,λ=8.5 mm) (c) S3(2h=10 mm,λ=4.3 mm) (d) S4(2h=20 mm,λ=18.7 mm) (a)U0=40 m/s (b)U0=60 m/s 图16尾缘锯齿对不稳定单音噪声的抑制(10°迎角) Fig.16Instabilitytonalnoisesuppressionwithtrailingedgeserrations[45] (a) 尾迹速度分布 (b) 湍流强度分布 Arina等[23]通过LES模拟并耦合FW-H方程的混合计算方法,研究了切开式锯齿尾缘对NACA65微弯叶片尾缘噪声的降噪。研究结果表明,锯齿形尾缘有效降低了低频范围内的尾缘噪声,最大可达10 dB,但是却增大了高频范围内的尾缘噪声。该结果与Gruber等[10]的实验结果相似。他们认为,锯齿形尾缘结构对尾缘附近流动的影响是噪声降低的主要原因,锯齿结构在尾缘附近产生了强烈并且结构复杂的旋涡流动现象,同时降低了尾缘附近的展向相干性。 国内外学者还研究了尾缘锯齿对真实叶片的降噪效果[27-28,46-47,98]。2016年,德国宇航院(DLR)的Jaron等[28]针对“洁净天空联合技术计划”中空客设计的AI-PX7开式转子,开展了尾缘锯齿降低开式转子干涉单音噪声的最优化研究,尾缘锯齿位于前面转子尾缘以减弱前面转子的尾迹,如图18所示。噪声计算通过定常计算结果和分析噪声预测模型完成。研究表明,尾缘锯齿可以降低开式转子干涉单音噪声约0.5 dB。不过,Jaron指出,这种通过定常计算结果和分析噪声预测模型进行的噪声预测不能够准确预测绝对的降噪量,这是由于锯齿周围流场强烈的三维特征造成的,进行更准确的噪声预测需要高精度的非定常模拟。采用尾缘锯齿后,前面转子尾迹速度亏损的幅值与相位沿转子展向产生明显振荡,Jaron等[28]认为速度亏损相位沿展向的振荡是噪声抵消的重要物理机制。同时,Jaron等还指出,宽频噪声也是开式转子的重要噪声源,尾缘锯齿对开式转子宽频噪声也将会产生影响,未来的工作是评估尾缘锯齿对开式转子宽频噪声的影响。 图18 针对AI-PX7开式转子的尾缘锯齿设计[28]Fig.18 Trailing edge serrations for AI-PX7 open rotor[28] 最近,Ryi[98]实验研究了常规尾缘锯齿与倾斜尾缘锯齿对缩比尺寸风力机转子噪声的影响,如图19所示。实验结果表明,常规尾缘锯齿可以成功降低风力机转子噪声2.79 dB(A),倾斜式尾缘锯齿可以降低风力机转子噪声2.22 dB(A)。 图19 带锯齿形尾缘的风力机缩比转子模型[98] Fig.19 Scaled model of wind turbine with trailing edge serrations[98] 在国内方面,吉林大学的陈坤[35]将尾缘锯齿用于轴流风机,获得了4.9 dB的降噪效果。西安交通大学的刘小民等[46]研究了尾缘锯齿对离心风机的降噪效果,数值模拟结果表明,尾缘锯齿可以降低离心风机噪声多达9.8 dB,采用仿生尾缘可以改变各截面尾迹涡的脱落位置,增大涡间距离,减小脱落涡对尾迹流动的扰动,降低叶片表面的压力脉动,最终使得尾迹涡引起的气动噪声显著减小。此外,上海交通大学郭晋之等[50-51]还研究了锯齿形尾缘对喷嘴噪声的影响。 为研究尾缘锯齿的降噪机理,近年来许多学者对锯齿尾缘结构的流场进行了详细测量[29-32],Vathylakis等[29]通过壁面传感器和液晶显示技术研究了锯齿尾缘的降噪机理,他们的实验研究结果表明,锯齿形尾缘能够增大尾缘附近的对流效应,但是锯齿结构附近的流向涡对流速度和展向相干性并没有得到很大的改变。Vathylakis等指出,锯齿两侧的倾斜壁面是噪声降低的关键所在,沿着倾斜壁面的涡对流速度要明显低于直尾缘叶片的流向涡对流速度,而这应和贴近倾斜壁面的旋涡流动现象有关,但是他们并未给出该旋涡流动现象的具体描述。Avallone等[31-32]利用时间分辨的层析粒子测速技术对带有尾缘锯齿的NACA0018翼型流场进行了详细测量与分析,测量了尾缘锯齿结构附近的湍流边界速度分布、三维涡结构、湍流脉动的频谱与空间分布、流动的展向相关性、流向对流速度分布、压力脉动源项分布等。Avallone的测量结果表明,中等迎角下,尾缘锯齿结构平均流场的一个主要特征是沿着锯齿边缘的流向对涡结构(图20),该对涡结构是由于翼型两侧的压力场以及锯齿边缘处的混合层引起的。该对涡结构会影响来流湍流感受到的尾缘锯齿结构的实际有效角度,这会导致尾缘锯齿的实际降噪效果不如理论预测结果。Avallone等[32]指出,在中等迎角下,尾缘锯齿已经导致较强的速度扰动,锯齿周围流场呈现出明显的三维性,湍流对流速度、壁面附近速度自功率谱与展向相关尺度均是流向位置的函数。这意味着在预测尾缘锯齿噪声时,分析模型中常用的翼型尾缘处是统计恒定不变的湍流流动分布这一假设(“冻结湍流”假设)需要进行进一步的修正以更好地预测尾缘锯齿结构的噪声。 图20 粒子图像测速仪与尾缘锯齿附近的流向对涡结构[32]Fig.20 PIV set-up and streamwise vortexes around the trailing edge serrations[32] 在理论研究方面,最近剑桥大学的Lyu[33]基于Amiet的尾缘噪声理论发展了一个预测尾缘锯齿噪声的半分析模型,该模型预测结果比Howe的尾缘锯齿模型更接近实验测量结果。Lyu指出,两个无量纲的几何参数主要影响尾缘锯齿的降噪效果:k1×2h与lz(f)/b,其中k1是弦长方向的波数,2h是锯齿的长度,b是锯齿的周期,lz(f)是翼型表面压力脉动的展向相关长度。研究发现,当k1×2h与lz(f)/b都远大于1时,远场噪声可以获得降低。这意味着在尾缘锯齿边缘处,保证不同散射压力波间显著相位差的最重要的一个参数是锯齿的根部到尖部的长度。此外,如果这些相位差的空间范围(即b)与展向方向的相关尺度相比足够小,辐射的声波之间将发生破坏性干涉,引起噪声的降低。 基于Lyu[33]的尾缘锯齿噪声预测模型, Fischer[99]提出了一种新的基于RANS的快速计算模型来预测尾缘锯齿的降噪效果,并通过对LN118翼型的风洞实验验证了该模型的有效性。该模型通过耦合Fischer提出的壁面压力计算模型与Lyu发展的尾缘锯齿远场噪声辐射模型对尾缘锯齿的降噪效果进行预测。风洞实验结果表明,尽管该模型预测的声压级比测量值小3 dB左右,但该模型可以较准确地预测不同尾缘锯齿结构的噪声差异,因而可以用于尾缘锯齿结构的最优化设计。 2017年,黄迅[34]基于Fourier展开与Wiener-Hopf方法提出了一个理论模型,该模型可以研究在均匀流情况下锯齿平板对声波的散射,如图21所示。研究发现锯齿状的平板相比正弦状平板可以更有效地抑制散射波,较大的锯齿波长与幅值可以更为有效地降低散射波。相比于锯齿波长,锯齿幅值对于散射波的影响更为重要。此外,锯齿对高频率下的入射波更为有效。该模型经过扩展也可以用来研究各种形状的前缘、尾缘造型对翼型前缘噪声和尾缘噪声的影响。 除了尾缘锯齿结构,近年来国外学者还提出模仿猫头鹰翅膀的新型仿生学结构,即小鳍栅栏结构与小鳍轨道结构,如图22所示[53]。2014年,Clark等[54]在研究猫头鹰结构时,实验中偶然发现模仿猫头鹰翅膀有柔软羽毛覆盖这一特征的“华盖”结构(如图23所示)可以降低翼型表面压力脉动多达30 dB。基于这个发现,Clark等[53]提出了可以模拟这种“华盖”结构效果并更适用于翼型的小鳍栅栏结构与小鳍轨道结构。小鳍栅栏结构与小鳍轨道结构安装在尾缘的上游,在边界层湍流被尾缘散射成声之前改变边界层湍流的特征。Clark等的实验结果表明,这些新型结构可以降低尾缘宽频噪声多达10 dB,如图24所示,并且这些仿生学结构的降噪效果对结构的参数不是很敏感,这意味着这些结构可以带来稳健的降噪效果。此外,这些结构在不同迎角下(从零升力迎角开始扩展9°迎角范围),均有良好的降噪效果,同时这些结构对翼型气动性能的影响非常小。 1000 Hz 2000 Hz 3000 Hz (a) 小鳍栅栏结构 (b) 小鳍轨道结构 图23 模仿猫头鹰柔翅膀的“华盖”结构[54]Fig.23 Canopy configuration similar to downy coating on the surface of the feather of owl[54] 图24 小鳍栅栏结构的降噪效果(翼型中间展向位置采用小鳍栅栏结构)Fig.24 Noise reduction effects of finlet fence (finlet fence is used in the mid-span)[53] 2017年, Avallone等[52]还研究了不同于常规尾缘锯齿结构的熨斗状锯齿,如图25所示。Avallone等的数值模拟结果表明,相比于常规的尾缘锯齿结构,熨斗状锯齿可以带来额外约2 dB的降噪效果[52]。研究发现,熨斗状锯齿可以带来额外降噪的原因是熨斗状锯齿可以使锯齿两侧的流体更加柔和的混合,进而降低锯齿根部的声源强度,如图26所示。 图25 常规尾缘锯齿与熨斗状锯齿[52] Fig.25 Conventional (a) and iron-shaped (b) trailing-edge serrations[52] 图26 声源等值面的对比(400 Hz)[52] Fig.26 Comparison of iso-surface of noise sources (400 Hz)[52] 叶片仿生学前缘降噪概念来自于人类对寂静飞行猫头鹰翅膀结构的认识以及座头鲸鳍肢前缘结构的认识。 20世纪70年代初,Hersh等[100-101]第一次公开发表了模拟猫头鹰翅膀前缘梳状结构降低机翼/叶片湍流噪声的研究结果(如图27所示),他们设计的锯齿形前缘结构降低了螺旋桨和机翼的噪声,实验测量结果表明前缘锯齿结构可以降低噪声4-5 dB。1972年,Arnd等[102]进一步实验研究了前缘锯齿构型对螺旋桨叶片降噪的效果,他们实验发现,前缘锯齿结构除了降低叶片湍流边界层脱落产生的随机噪声之外,由于前缘锯齿对螺旋桨叶片流场的控制,也可以降低螺旋桨旋转噪声。1974年,GE公司的Smith和Sowers等[103]首次将前缘锯齿构型用于风扇/压气机叶栅降噪,通过对多种流动状态和锯齿构型的实验研究,他们发现采用6%弦长的锯齿构型设计可以有效降低叶栅噪声,同时也保证气动损失也最小。2011年,俄罗斯空气动力研究所的Kopiev[104]将锯齿结构用于机翼前的缝翼,他们实验研究了锯齿形缝翼对机翼气动性能与噪声的影响。实验结果表明锯齿形缝翼可以在70°~130°极方位角内降低宽广频率范围内的机翼噪声。2016年,德国勃兰登堡州工业大学的Geyer[105]还研究了模仿猫头鹰前缘梳状结构的翼型对前缘干涉噪声的影响(如图28所示),研究发现梳状结构可以降低翼型低频范围内的噪声,而高频范围内的噪声稍有增大。 图27 模仿猫头鹰翅膀的前缘锯齿构型[100-101]Fig.27 Leading edge serrations that imitate owl feathers[100-101] 图28 模仿猫头鹰的前缘梳状结构翼型[105] Fig.28 Airfoil with leading edge serrations that imitate owl feathers[105] 众所周知,无论是为了适应不同来流方向(来流迎角)的需要,还是机翼加温除冰需要,或者叶片增强抗冲击的需要,飞机机翼和发动机叶片的前缘都是相对厚实的钝头形状,因此在机翼和叶片前缘构造如图27、图28所示的具有尖锐锯齿形状的猫头鹰翅膀前缘梳状结构,其工程实现和应用都具有一定难度和局限。近年来,针对机翼和叶片前缘降噪,人们逐渐将研究工作重点瞄准对座头鲸鳍肢的前缘凸起结构的模仿。1995年,在国际著名的Journal of Morphology上, Fish等[55]首次发表了对座头鲸鳍肢前缘凸起结构的流体动力学性能研究,他们发现座头鲸具有与其庞大体积不相称的敏捷的机动能力,并首次对座头鲸鳍肢的前缘凸起(我们称之为波浪状前缘结构)做了详细的测量。其后很多研究者研究了波浪形前缘翼型/叶片的空气动力学特性[56-60],研究结果表明,这些波浪状前缘起着类似于增升装置的作用,可以控制流过鳍肢的水流,在大的迎角下保持升力。 由于前缘锯齿造型无疑会对叶片和叶型流场造成明显影响,因此除了研究前缘锯齿降噪性能之外,许多研究者还对前缘锯齿控制叶片和叶型流场的特性进行了研究,1981年Collins等[61]研究了前缘锯齿结构控制机翼边界层的情况,他们发现,在没有增大叶型阻力的情况下,采用前缘锯齿可以增大NACA0012叶型升力12%,增大NACA2412叶型升力22%。之后,采用前缘锯齿结构控制低雷诺数机翼流场并增大升力成为低雷诺数叶型研究的重要内容。 表2列举了近年来针对前缘锯齿/波浪形仿生学结构降噪效果和降噪机理开展的主要研究工作。下面分别从前缘锯齿/波浪形仿生学构型对气动性能的影响、对层流边界层不稳定噪声的影响、对湍流干涉噪声的影响等三个方面,评述过去十多年来研究工作的进展情况。 图29 座头鲸鳍肢前缘的特殊结节结构[106] Fig.29 Special tubercles on pectoral flipper leading edges of humpback whales [106] 表2 仿生学波浪形前缘降噪研究Table 2 Studies on noise reduction using bionic wavy leading edges 如前文所述,波浪形前缘受启发于座头鲸鳍肢,被认为是一种增升减阻装置[55]。座头鲸鳍肢及其解剖学分析如图30所示。在Fish早期的形态学研究之后,许多学者开始研究波浪形前缘对翼型气动及水力性能的影响。大多数研究表明,波浪形前缘可以推迟失速的发生,增加过失速状态升力,减小过失速状态阻力并可以减小层流分离泡的长度,但是也会降低翼型预失速状态下的气动性能[62-71]。 图30 座头鲸鳍状肢解剖学分析[55] Fig.30 Anatomical analysis of humpback whale pectoral flipper[55] 图31 模仿座头鲸鳍肢的风力发电机桨叶及机翼前缘锯齿结构[62] Fig.31 Wind turbine blades and airfoil that imitate humpback whale pectoral flipper[62] Miklosovic等实验研究了波浪形前缘对翼型气动性能的影响,发现波浪形前缘可以将失速角推迟近40%,并且可以增加升力,减小阻力[62]。Zhang等实验研究了低雷诺数状态下一定迎角范围内正弦形前缘凸起结构对翼型气动性能的影响,发现波状凸起可以有效地抑制翼型失速,翼型过失速状态下气动性能得到大幅度提高,阻力系数减小了20%,升力系数增加了25%,升阻比最大增加39.2%。然而,波形凸起一定程度上损害了预失速状态下的气动性能[59]。波浪形前缘类似于小尺度的旋涡发生器,可以诱导流向涡的产生,增强边界层内的动量和能量交换,控制边界层的分离,提高翼型气动性能。 2011年,Fish[111]等构想了未来的应用前缘锯齿结构的飞机模型,如图33所示。由于前缘锯齿结构可以增加升力,减小阻力,并可以改善失速性能,提高飞行稳定性,所以可以考虑减少缝翼、襟翼等增升装置的使用,这样就可以大大降低飞机起飞及进场时的增升装置噪声。 图32 直叶片和波状前缘叶片示意图[59]Fig.32 Sketch of airfoil with straight leading edge and wavy leading edge[59] 图33 飞机及螺旋桨的前缘锯齿结构[111]Fig.33 Aircraft and propeller with wavy leading edges[111] 近年来,Shinichiro(2009)[65]和Cranston(2012)[66]等在低速风洞中实验分析了前缘锯齿结构对机翼的流动控制和增升特性。特别是,Corsini等(2013)[60]研究了正弦形波浪前缘提高风扇抗失速特性的能力(如图34所示),他们的研究结果表明,对于三维风扇叶片,正弦形波浪前缘可以明显提高风扇的抗失速能力,特别是在风扇峰值压比状态,采用波浪形前缘还可以小幅度提高风扇效率。 图34 仿生学波浪前缘风扇叶片[60] Fig.34 Bionic fan blade with wavy leading edges[60] 除了气动性能方面的研究,波浪形前缘也用于降低翼型尾缘自噪声和前缘干涉噪声。Brooks 指出层流边界层-涡脱落噪声是翼型尾缘噪声的主要产生机制之一[112]。从本质上来讲,涡脱落噪声是由翼型表面层流边界层的不稳定性引起的。不稳定T-S波与尾缘干涉辐射噪声,声波向上游传播,加强边界层内的不稳定性,完成声学反馈回路。层流边界层不稳定噪声由窄带的单音噪声主导。许多学者对层流边界层不稳定噪声的产生机理及其降噪进行了研究[72,85,107,113-117]。Longhouse实验测量了某型低速轴流风扇的气动和声学性能,并采用波状锯齿以降低涡脱落噪声[107],研究表明,无论将锯齿放置于前缘,中间弦向位置还是吸力面尾缘均可以显著地降低涡脱落噪声。Hansen 等实验研究了波浪形前缘对NACA0021翼型层流边界层噪声的影响,发现振幅越大波长越小降噪效果越明显[72]。乔渭阳等实验研究了波浪形前缘对NACA0012翼型不稳定噪声的影响,也发现振幅越大波长越小越能显著降低不稳定单音噪声[85]。不稳定噪声的降噪机制与波谷处的流向涡有关,流向涡的产生增强了边界层内的动量交换,影响了边界层的稳定性,能削弱甚至能完全破坏声学反馈回路。 (a) 实验设置 (b) 波浪前缘翼型 (c) 波浪前缘幅值的影响 (d) 波浪前缘周期的影响 采用波浪形前缘的研究重点是降低湍流与翼型/叶片干涉的噪声。许多研究者发现,仿照座头鲸的波状前缘结构,既可以使翼型的失速性能得到改善,同时还能够有效降低湍流与机翼/叶片前缘干涉噪声。2011年,法国宇航院(ONERA)Polacsek等[73]实验研究了湍流与NACA651210独立翼型干涉噪声,发现在实验速度范围内,采用正弦波浪结构,能够有效降低湍流-翼型干涉噪声3~4 dB。2012年Gruber等[74]研究发现,在串列翼型上同时应用波状前缘与尾缘锯齿结构,可以降低翼型噪声5~8.5 dB,进一步研究表明,其降噪效果主要是来自于下游翼型前缘与上游叶片尾迹干涉噪声的降低,波浪形前缘可以减弱翼型对来流湍流的响应。2012年,Clair等[118]实验和数值模拟研究了波浪形前缘对湍流-翼型干涉噪声的影响,他们的研究结果表明,波浪形前缘能够有效降低湍流-翼型前缘干涉噪声3~4 dB。 2013年,Roger等[119]采用扩展的Amiet前缘噪声理论,研究了波状前缘结构以及多孔介质材料对湍流-翼型干涉噪声的抑制效果,研究发现,波浪状前缘结构可以在斯特劳哈尔数(基于翼型弦长)1~40范围内有效降低湍流-翼型干涉噪声,针对湍流条件下的湍流-翼型干涉,波状前缘结构可以降低湍流-翼型干涉噪声达到10 dB;针对圆棒尾迹-翼型干涉,波状前缘结构可降低噪声5~6 dB。 近年来,英国南安普顿大学声学与振动研究所(ISVR)针对波浪形前缘降噪机理和降噪关键设计参数进行了系统的实验和数值模拟研究工作[75-81, 108-109,120]。2013年,Clair等[75]首先采用实验测量与CAA数值模拟的方法,系统研究了正弦形波浪前缘结构对湍流-翼型前缘干涉噪声的抑制效果,研究发现,在对翼型气动性能没有显著影响的条件下,在实验速度范围内,波浪形前缘结构可以降低噪声3~4 dB。2013年,Lau等[108-109]采用高精度数值模拟方法,研究了波状前缘对阵风-翼型干涉噪声的影响,他们针对波浪形前缘结构参数(波长、峰高等)进行了详细的参数化计算分析,研究发现,波状前缘大小(波峰高度A)与阵风纵向波长(λ)的比值(A/λ)是影响波状前缘降噪效果最重要的参数,而波浪前缘的波长参数对阵风-翼型干涉噪声降低效果影响不大。他们认为,波状前缘结构能够降低翼型阵风干涉噪声的原因可能在于波浪状前缘导致不同展向位置对来流阵风的响应时间不一致,引起叶片表面压力脉动减小,从而降低翼型阵风干涉噪声。 2014年,Haeri等[79]采用数值模拟方法,分别研究了入射湍流与直前缘平板干涉噪声以及入射湍流与波浪状前缘平板的干涉噪声,研究结果表明,波浪状前缘平板可以最大降低噪声3.7 dB。图36是直前缘平板与波浪前缘平板声场的对比。研究发现,波浪状前缘可以降低平板表面压力脉动的相关尺度,并且导致平板前缘附近涡的变形,他们认为这正是波浪状前缘降低湍流干涉噪声的物理机制所在。此外,他们还发现,波浪前缘幅值增大到一定程度后,继续增大就不会进一步增大降噪量。 (a) 直前缘平板声场 (b) 波浪前缘平板声场 2015年,Narayanan等[76-77]用实验的方法研究了波浪状前缘对湍流-翼型(平板)前缘干涉宽频噪声的抑制效果,图37是其仿生学波浪前缘平板与波浪形翼型实验件。实验结果表明,在频率小于300 Hz的范围,波浪形前缘的降噪效果并不明显,但是在中等频率范围内(300~4000 Hz),波浪形前缘可以显著降低湍流-翼型干涉宽频噪声,波浪前缘最大可以降低湍流-平板干涉宽频噪声约9 dB,而相同的波浪前缘结构对真实NACA65翼型的湍流-翼型干涉噪声的降噪效果要稍小,约为7 dB(如图38所示),他们的研究结果还表明,波浪前缘的波浪幅值是影响降噪的关键参数,而波浪前缘周期对降噪效果影响较弱,随着波浪幅值增加,降噪效果也相应增加。 (a) 仿生学波浪前缘平板 (b) 仿生学波浪前缘翼型 图38 仿生学波浪前缘对平板与翼型的降噪效果[77]Fig.38 Noise reduction effects of bionic wavy leading edge on flat plate and airfoil[77] 2016年,ISVR的Kim等[81]通过求解全三维无黏Euler方程,数值研究了波浪形前缘对平板翼型-湍流干涉噪声的影响,来流湍流为数值合成的均匀各向同性湍流,如图39所示。他们主要系统地研究了锯齿振幅对降噪效果的影响,因为他们同样认为锯齿振幅是提高降噪效果的关键参数,研究发现声功率降噪量几乎与锯齿振幅成正比。他们指出波浪形前缘降噪机制主要包括两个方面:由几何倾斜而引起的“源截止效应”以及翼型前缘的相位干涉效应。 Turner(2016年)[120]采用高精度数值模拟的方法对波浪前缘的降噪机理进行了研究,并给出了波浪前缘附近涡系的物理解释,如图40所示。 最近,ISVR的Chaitanya等[78]还提出了新型仿生学结构——双周期波浪前缘结构(图41)以及开槽式波浪前缘结构(图42)。研究表明,这些新型仿生学结构可以进一步增大降噪效果。 (a) 合成来流湍流 (b) 网格 (c) 降噪效果 图40 波浪前缘附近涡系的物理描述[120]Fig.40 Physical description of the vortices system around the wavy leading edge[120] 图41 双周期波浪前缘结构[78]Fig.41 Double-wavelength wavy leading edge structure[78] 图42 开槽式波浪前缘结构[78]Fig.42 Slitted-root wavy leading edge structure[78] 剑桥大学Mathews等[83](2015年)和Lyu等[84](2016年)采用理论分析的研究方法研究了波浪形前缘结构对湍流-翼型干涉噪声的抑制效果与抑制机理。Mathew[83]通过考虑前缘压力散射这一问题来分析湍流与翼型的干涉噪声,发展了既能够预测涡干涉又能够预测湍流干涉的前缘锯齿噪声辐射模型,该模型进一步确定了前缘锯齿的降噪效果(如图43所示)。不过,Mathew也指出,确定降低噪声的最佳前缘锯齿形状是很困难的。Lyu[84]基于Fourier展开与Schwarzschild方法,对Amiet的经典前缘噪声预测模型进行了发展,发展的新模型能够考虑前缘为锯齿形的情况,可以预测锯齿前缘对二维平板(或翼型)湍流干涉噪声的降噪效果。在中高频率范围,模型的预测结果与实验结果吻合非常好,可以准确预测出前缘锯齿对翼型5~10 dB的降噪效果,如图44所示。此外,Lyu还用发展的前缘锯齿噪声预测模型对前缘锯齿的长度(2h)与周期(b)进行了初步的参数化研究,研究发现,当锯齿长度小于1/3湍流流向积分尺度时,几乎没有降噪效果,随着锯齿长度增大,降噪效果变得明显;锯齿周期b很大时,几乎没有降噪效果,只有当锯齿周期b小于湍流流向积分尺度时,高频才能够观察到噪声降低,锯齿周期b越小,降噪效果越明显。Lyu认为,前缘锯齿的降噪机理与尾缘锯齿的降噪机理相同,即锯齿结构存在时叶片表面的散射压力产生破坏性干涉,进而降低叶片辐射噪声。 图43 直前缘与波浪前缘散射压力的对比[83]Fig.43 Comparison of the scattered pressure by the straight leading edge and wavy leading edge[83] 图44 前缘锯齿对翼型-湍流干涉噪声影响的理论研究[84]Fig.44 Theoretical study on the effects of serrated leading edge on the airfoil-turbulence interaction noise[84] 2015年,Narayanan 等实验研究了波浪形前缘对平板翼型-湍流前缘干涉噪声的影响,来流湍流为采用湍流格栅生成的均匀各向同性湍流[77]。研究发现降噪效果在低频不明显,而在500~8000 Hz的中频范围内较明显,如图45所示。他们同时对锯齿振幅和波长进行了参数化研究,发现声功率降噪量对锯齿振幅比较敏感,而对锯齿波长不敏感。Lau等采用高精度数值方法研究了波浪形前缘对翼型-阵风干涉噪声的影响,得到了相似的结论[121]。 图45 波浪形前缘对翼型-各向同性湍流干涉噪声的影响的实验研究[77]Fig.45 Experimental study on the effects of wavy leading edge on airfoil-isotropic turbulence interaction noise[77] Aguilera采用了数值方法研究了波浪形前缘对翼型-各向异性湍流干涉噪声的影响[82]。来流湍流为采用湍流合成方法生成的全三维无散均匀各向异性湍流(如图46所示),声场采用线化Euler方程直接数值求解。此文主要研究了中等尺度湍流对波浪形NACA0012翼型噪声辐射的影响,此中等尺度的湍流类似于航空发动机风扇尾迹内的各向异性湍流。Aguilera主要关注声源附近湍流结构的变形及速度谱、翼型表面的非定常压力及其谱密度、声源处速度脉动和压力脉动的相干以及不同各向异性程度下声源的展向相关性。数值研究结果表明,湍流长度尺度的些许变化就可以非常明显地改变波峰和波谷处声源频谱形状。最大声源总是位于波谷处,此声源主要受横向速度脉动的影响。为了减小波峰和波谷声源的相关性,湍流流向长度尺度与锯齿振幅之比以及湍流展向长度尺度与锯齿波长之比应分别满足如下条件:lx/(2hw)<1,lz/λw≤0.5。 相对于实验中湍流格栅生成的均匀各向同性湍流以及数值生成的均匀各向异性湍流,圆柱尾迹区的非均匀各向异性湍流在工程应用中更为普遍。乔渭阳等[122]研究了波浪形前缘对圆柱-翼型干涉噪声的影响。研究表明,前缘锯齿振幅越大波长越小降噪效果越明显,降噪效果主要集中在卡门涡街脱落频率之后的中高频段,最大降噪量约为4 dB(如图47所示)。值得注意的是,由于设计的锯齿振幅有限(弦长的10%),波浪形前缘对脱落涡主频噪声降噪效果不明显,可以预测,更大的锯齿振幅可以降低脱落涡主频噪声。 (a) 各向异性湍流入射平面 (b) 波浪形前缘翼型及湍流长度尺度示意图 (a) 实验装置 (b) 波浪前缘的降噪效果 本文总结分析和评述了到目前为止过去十多年来仿生学气动噪声控制技术的发展。可以看出,尽管国内外的仿生学降噪研究工作取得了很大进展,但是,目前针对湍流噪声的仿生学降噪理论和技术的认识仍然具有明显的不足,如果以降低飞机/航空发动机湍流宽频噪声的目标来看,目前的仿生学降噪理论与实际工程应用仍然存在着巨大差距,仿生学降噪理论仍然处于学术探索阶段。笔者认为仿生学气动噪声控制理论和技术目前的主要问题及研究的重点在以下几个方面: 1) 对仿生学构型的降噪机理仍不透彻,没有达到统一的认识。关于尾缘锯齿的设计仍未给出统一的指导规律,有关锯齿长度、锯齿周期等对宽频噪声降噪效果影响规律既有与Howe的理论一致的研究结论,也有相互矛盾的结论。例如Chong等研究结果表明,尽管锯齿周期越小时,对宽频噪声的降噪效果越好,但同时由于钝尾缘效应产生的脱落涡单音噪声越大,最终的效果是锯齿周期较大反而比较好。不同的研究者针对不同的对象得出的结论有所不同,对尾缘锯齿降噪的研究还未成熟,对尾缘锯齿降噪的规律仍未取得统一的认识。近年来,随着对航空发动机风扇转静干涉、对转开式转子叶片相互干涉等叶片尾迹湍流与下游叶片前缘干涉噪声问题的关注,即“湍流-叶片干涉噪声”,国际上许多研究机构都开始重视采用仿生学前缘构型进行噪声控制,许多研究结果都表明,波浪形或者锯齿形前缘结构能够有效降低湍流-叶片干涉噪声。但是,类似于尾缘降噪研究,由于湍流问题本身复杂性,而仿生学构型往往牵涉到非常微小尺度的湍流细节和发声过程,使得目前对前缘仿生学构型的降噪机理仍不透彻,对于波浪形前缘和锯齿形前缘影响湍流发展以及湍流发声过程的物理机制也还没有达到完全统一的认识。 2) 到目前为止,几乎所有研究工作及其理论都是针对二维翼型、二维叶片或者二维平面叶栅,仅有的成功工程应用是对风力发电机叶片,就作者对国内外研究状况的认识,还未见到应用仿生学原理进行三维机翼/叶片宽频噪声的研究。而众所周知,真实飞机机翼、航空发动机叶片(风扇、压气机、涡轮等)具有强三维流动的基本特征,特别是发动机叶片构型采用强三维构型设计,毫无疑问,强三维叶片构型和强三维的流动过程,会显著影响仿生学构型的流动和声学原理,也会影响到仿生学构型的降噪机理。 3) 针对飞机气动噪声问题,最为关心的是飞机在起飞/降落阶段的气动噪声辐射,因此针对飞机机体气动噪声研究,普遍关心的是飞行速度比较低(马赫数0.3范围)、雷诺数较低的气动噪声问题,Lilley教授对飞机与展翅飞翔鸟类的类比研究也是针对低速低雷诺数飞行状态。但是,必须注意的是,目前飞机主要噪声源仍然是航空发动机噪声,而不论是飞机起飞、降落还是巡航状态,发动机内部气流的速度远高于展翅飞翔鸟类的飞行速度,针对发动机气动噪声问题必须考虑到高速、高雷诺数的流动状态。众所周知,高速高雷诺数状态湍流运动的脉动频率远大于低雷诺数湍流,而旋涡尺度、湍流相干尺度等都远小于低雷诺数湍流,毫无疑问,针对高速高雷诺数湍流控制及其湍流噪声控制将需要更为精细化的仿生学构型,这是仿生学气动噪声控制必须重视和面对的问题。 综上所述,基于仿生学的气动噪声控制原理及其工程应用,仍然需要做更为深入的研究,特别是,由于3D打印等高精机械加工技术的不断进步,开展能够精细模拟生物特殊构型的新型仿生学降噪结构的创新研究,特别值得持续关注和研究。用著名的Lilley教授的话结束本文,“如果我们忽视猫头鹰等生物低噪声飞行背后隐藏的特殊物理机制与科学机理研究,我们将会错失设计未来安静飞行器的黄金机会”。 [1]Qiao W Y, Wang L F, Aero-engine aeroacousitcs[M]. Xi’an: Northwestern Polytechnical University Press, 2016: 1-10. (in Chinese)乔渭阳, 王良锋. 航空发动机气动声学(第二版)[M]. 西安: 西北工业大学出版社, 2016: 1-10 [2]Zhu Z Q, Lan S L. Study of airframe noise and its reduction for commercial aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 406-421. (in Chinese)朱自强, 兰世隆. 民机机体噪声及其降噪研究[J]. 航空学报, 2015, 36(2): 406-421 [3]Logue M M, Atassi H M. Passive control of fan broadband noise[C]//15th AIAA/CEAS Aeroacoustics Conference. AIAA 2009-3149 [4]Moreau A, Enghardt L. Ranking of fan broadband noise sources based on an experimental parametric study[C]//15th AIAA/CEAS Aeroacoustics Conference. AIAA 2009-3222 [5]Howe M S. Aerodynamic noise of a serrated trailing edge[J]. Journal of Fluid and Structures, 1991, 5(1): 33-45 [6]Howe M S. Noise produced by a sawtooth trailing edge[J]. Acoustical Society of America Journal, 1991, 90(1): 482-487 [7]Dassen T, Parchen R, Bruggeman J, et al. Results of a wind tunnel study on the reduction of airfoil self-noise by the application of serrated blade trailing edges[R]. Germany: NLR, NLR TP 96350, 1996 [8]Braun K A, Van der Borg N J C M, Dassen A G M, et al. Noise reduction by using serrated trailing edges[C]//European wind energy conference, Germany. Dublin, 1997 [9]Oerlemans S, Fisher M, Maeder T, et al. Reduction of wind turbine noise using optimized airfoils and trailing-edge serrations[J]. AIAA Journal, 2009, 47(6): 1470-1481 [10]Gruber M. Airfoil noise reduction by edge treatments[D]. University of Southampton, 2012 [11]Gruber M, Azarpeyvand M, Joseph P F. Airfoil trailing edge noise reduction by the introduction of sawtooth and slitted trailing edge geometries[C]//Proceedings of 20th International Congress on Acoustics. Sydney, 2010: 23-27 [12]Gruber M, Joseph P F, Chong T P. Experimental investigation of airfoil self noise and turbulent wake reduction by the use of trailing edge serrations[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2010-3803 [13]Gruber M, Joseph P, Chong T. On the mechanisms of serrated airfoil trailing edge noise reduction[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2011-2781 [14]Gruber M, Joseph P F, Azarpeyvand M. An experimental investigation of novel trailing edge geometries on airfoil trailing edge noise reduction[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2013-2011 [15]Chong T P, Joseph P, Gruber M. An experimental study of airfoil instability noise with trailing edge serrations[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2010-3723 [16]Chong T P, Joseph F, Gruber M. On the airfoil self-noise reduction by trailing edge serrations of non-insertion type[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2012-2185 [17]Chong T P, Vathylakis A, Joseph P, et al. On the noise and wake flow of an airfoil with broken and serrated trailing edges[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2011-2860 [18]Chong T P, Joseph P F. An experimental study of airfoil instability tonal noise with trailing edge serrations[J]. Journal of Sound & Vibration, 2013, 332(24): 6335-6358 [19]Chong T P, Joseph P F, Gruber M. Airfoil self noise reduction by non-flat plate type trailing edge serrations[J]. Applied Acoustics, 2013, 74(4): 607-613 [20]Chong T P, Vathylakis A. On the aeroacoustic and flow structures developed on a flat plate with a serrated sawtooth trailing edge[J]. Journal of Sound & Vibration, 2015, 354(10): 65-90 [21]Moreau D J, Brooks L A, Doolan C J. On the noise reduction mechanism of a plate serrated trailing edge at low-to-moderate Reynolds number[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2012- 2186 [22]Moreau D J, Doolan C J. Tonal noise from trailing edge serrations at low reynolds number[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2013-2010 [23]Arina R, Rinaldi R D R, Iob A. Numerical study of self-nosie produced by an airfoil with trailing edge serrations[C]//18th AIAA/CEAS Aeroacoustics Conference. AIAA 2012-2184 [24]Jones L E, Sandberg R D. Numerical investigation of airfoil self-noise reduction by addition of trailing-edge serrations[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2010-3703 [25]Jones L E, Sandberg R D. Acoustic and hydrodynamic analysis of the flow around an aerofoil with trailing-edge serrations[J]. Journal of Fluid Mechanics, 2012, 706(43): 295-322 [26]Finez A, Jondeau E, Roger M, et al. Broadband noise reduction of a linear cascade with trailing edge serrations[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2011-2874 [27]Weckmüller C, Guerin S. On the influence of trailing-edge serrations on open-rotor tonal noise[C]//18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO. AIAA2012-2124 [28]Jaron R, Moreau A, Guerin S, et al. Optimization of trailing-edge serrations to reduce open-rotor tonal interaction noise[C]//Proceeding of the ISROMAC, 2016 [29]Vathylakis A, Chong T P. On the turbulent boundary layers developed on flat plate with a serrated trailing edge[C]//19th AIAA/CEAS Aeroacoustics Conference. AIAA 2013-2107 [31]Leon C A, Avallone F, Pröbsting S, et al. PIV investigation of the flow past solid and slitted sawtooth serrated trailing edges[C]//AIAA Aerospace Sciences Meeting, AIAA Scitech, 2016 [32]Avallone F, Pröbsting S, Ragni D. Three-dimensional flow field over a trailing-edge serration and implications on broadband noise[J]. Physics of Fluids, 2016, 28(117101): 3818-3831 [33]Lyu B, Azarpeyvand M, Sinayoko S. Prediction of noise from serrated trailing edges[J]. Journal of Fluid Mechanics, 2015, 793: 556-588 [34]Huang X. Theoretical model of acoustic scattering from a flat plate with serrations[J]. Journal of Fluid Mechanics, 2017, 819: 228-257 [35]Chen K. Morphology, flight kinematics and bionics of silent flight owl[D]. Jilin University, 2012. (in Chinese)陈坤. 三种鸮形态学、飞行运动学特征规律及其仿生研究[D]. 吉林大学, 2012 [36]Sun S M, Ren L Q, Xu C Y. Research on coupling sound absorption property of owl skin and feather[J]. Noise and Vibration Control, 2008, (3): 119-123. (in Chinese)孙少明, 任露泉, 徐成宇. 长耳鸮皮肤和覆羽耦合吸声降噪特性研究[J]. 噪声与振动控制, 2008, (3): 119-123 [37]Ji L, Qiao W Y, Wang L F, et al. Experimental investigation of airfoil trailing-edge noise reduction in a normal indoor test bed[J]. Journal of Propulsion Technology, 2015, (5): 703-712. (in Chinese)纪良, 乔渭阳, 王良峰, 等. 普通室内机翼尾缘噪声降噪的实验研究[J]. 推进技术, 2015, (5): 703-712 [38]Qiao W Y, Ji L, Xu K B, et al. An Investigation on the near-field turbulence and radiated sound for an airfoil with trailing edge serrations[C]//19th AIAA/CEAS Aeroacoustics Conference. AIAA 2013-2112 [39]Ji L, Qiao W Y, Tong F, et al. Experimental and numerical study on noise reduction mechanisms of the airfoil with serrated trailing edge[C]//20th AIAA/CEAS Aeroacoustics Conference, Atlanta, Georgia. AIAA 2014-3297 [40]Qiao W Y, Ji L, Tong F, et al. Experimental and numerical study on noise reduction mechanisms of the linear cascade with serrated trailing edge[C]//20th AIAA/CEAS Aeroacoustics Conference, Atlanta, Georgia. AIAA 2014-3349 [41]Tong F, Qiao W Y, Wang L F, et al. Noise reduction mechanism of bionic airfoil trailing edge serrations[J]. Acta Aeronautica et Astronautica Sinica, 2015, (9): 2911-2922. (in Chinese)仝帆, 乔渭阳, 王良锋, 等. 仿生学翼型尾缘锯齿降噪机理[J]. 航空学报, 2015, (9): 2911-2922 [42]Tong F, Qiao W Y, Wang L F, et al. Numerical study of fan turbulence broadband noise’s characteristics[J]. Journal of Aerospace Power, 2016, (4): 894-902. (in Chinese)仝帆, 乔渭阳, 纪良, 等. 尾缘锯齿降低叶栅噪声的数值模拟[J]. 航空动力学报, 2016, (4): 894-902 [43]Tong F, Qiao W Y, Ji L, et al. Experimental study on the turbomachinery trailing edge noise reduction[C]//Proceedings of ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, South Korea. GT 2016-56453 [44]Tong F, Wang X N, Wang L F, et al. Experimental study on airfoil noise reduction with trailing edge serrations under various incoming flow conditions[C]//Proceedings of the 3nd Symposium on Fluid-Structure-Sound Interactions and Control. Perth, Western Australia, 2015, A027 [45]Chen W J, Qiao W Y, Tong F, et al. Blade boundary layer instability noise with trailing edge serrations[J]. Acta Aeronautica et Astronautica Sinica, 2016, (11): 3317-3327. (in Chinese)陈伟杰, 乔渭阳, 仝帆, 等. 尾缘锯齿结构对叶片边界层不稳定噪声的影响[J]. 航空学报, 2016, (11): 3317-3327[46]Liu X M, Tang H, Wang X, et al. Noise reduction mechanism of bionic coupling blade based on the trailing edge of Goshawk wing[J]. Journal of Xi’an Jiaotong University, 2012, 46(1): 35-41. (in Chinese)刘小民, 汤虎, 王星, 等. 苍鹰翼尾缘结构的单元仿生叶片降噪机理研究[J]. 西安交通大学学报, 2012, 46(1): 35-41 [47]Gong W Q, Wang F, Tian Z L, et al. Experimental study of the effect of serrated blade trailing edge on axial fan noise reduction in an outdoor air conditioner[J]. Journal of Engineering Thermophysics, 2011, 32(10): 1681-1684. (in Chinese)宫武旗, 王芳, 田镇龙, 等. 叶片锯齿尾缘对降低空调室外机气动噪声影响的试验研究[J]. 工程热物理学报, 2011, 32(10): 1681-1684 [48]Huang Q. A numerical study of the flow around airfoils with serrated trailing edges and aerodynamic noise based on large eddy simulation[D]. Beijing: Tsinghua University, 2015. 黄乾. 基于大涡模拟的锯齿尾缘翼型流动分析及气动噪声预测[D]. 北京: 清华大学, 2015 [49]Xu Y B, Li X D. An experiment study of the serrated trailing edge noise[J]. Acta Aerodynamica Sinica, 2012, 30(1): 120-124. (in Chinese)许影博, 李晓东. 锯齿型翼型尾缘噪声控制实验研究[J]. 空气动力学学报, 2012, 30(1): 120-124 [50]Guo J Z, Ou-yang H, Tian J, et al. Analysis of aerodynamic acoustic characteristics of chevron nozzles[J]. Noise and Vibration Control, 2013, 33(5): 204-209. (in Chinese)郭晋之, 欧阳华, 田杰, 等. 锯齿形尾缘喷嘴气动声学实验及数值分析[J]. 噪声与振动控制, 2013, 33(5): 204-209 [51]Guo J Z. Investigation on mixing enhancement and noise reduction mechanism of chevron nozzle[D]. Shanghai Jiao Tong University, 2013. (in Chinese)郭晋之. 锯齿形尾缘喷嘴射流增混与降噪机理研究[D]. 上海交通大学, 2013 [52]Avallone F, Velden W C P V D, Ragni D. Benefits of curved serrations on broadband trailing-edge noise reduction[J]. Journal of Sound & Vibration, 2017, 400: 167-177 [53]Clark I, Alexander W N, Devenport W J, et al. Bio-inspired trailing edge noise control[C]//21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX. AIAA 2015-2365 [54]Clark I, Devenport W J, Jaworski J, et al. The noise generating and suppressing characteristics of bio-inspired rough surfaces[C]//20th AIAA/CEAS Aeroacoustics Conference. AIAA 2014-2911 [55]Fish F E, Battle J M. Hydrodynamic design of the humpback whale flipper[J]. Journal of Morphology, 1995, 225: 51-60 [56]Miklosovic D S, Murray M M, Howle L E. Experimental evaluation of sinusoidal leading edges[J]. Journal of Aircraft, 2007, 44(4): 1404-1408 [57]Van Nierop E A, Alben S, Brenner M. How bumps on whale flippers delay stall: an aerodynamic model[J]. Physical Review Letters, 2008, 100(5): 1-4 [58]Yoon H S, Hung P A, Jung J H, et al. Effect of the wavy leading edge on hydrodynamic characteristics for flow around low aspect ratio wing[J]. Computers & Fluids, 2011, 49(1): 276-289 [59]Zhang X, Zhou C, Tao Z, et al. Numerical study on effect of leading-edge tubercles[J]. Aircraft Engineering & Aerospace Technology, 2013, 85(4): 247-257 [60]Corsini A, Delibra G, Sheard A G. The application of sinusoidal blade-leading edges in a fan-design methodology to improve stall resistance[J]. Proceedings of the Institution of Mechanical Engineers Part A Journal of Power & Energy, 2013, 228(3): 255-271 [61]Collins F G. Boundary-layer control on wings using sound and leading-edge serrations[J]. AIAA Journal, 1981, 19(2): 129-130 [62]Miklosovic D S, Murray M M, Howle L E, et al. Leading-edge tubercles delay stall on humpback whale (Megaptera novaeangliae) flippers[J]. Physics of Fluids, 2004, 16(5): L39-L42 [63]Johari H, Henoch C W, Custodio D, et al. Effects of leading-edge protuberances on airfoil performance[J]. AIAA Journal, 2007, 45(11): 2634-2642 [64]Hansen K L, Kelso R M, Dally B B. Performance variations of leading-edge tubercles for distinct airfoil profiles[J]. AIAA Journal, 2011, 49(1): 185-194 [65]Shinichiro I T O. Aerodynamic influence of leading-edges serrationos on an airfoil in a low Reynoldys number[J]. Journal of Biomechnical Science and Engineering, 2009, 4(1): 117-123 [66]Cranston B, Laux C, Altman A. Leading edge serrations on flat plates at low reynolds number[C]//AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. AIAA 2012-0053 [67]Yoon H S, Hung P A, Jung J H, et al. Effect of the wavy leading edge on hydrodynamic characteristics for flow around low aspect ratio wing[J]. Computers & Fluids, 2011, 49(1): 276-289 [68]Weber P W, Howle L E, Murray M M, et al. Computational evaluation of the performance of lifting surfaces with leading-edge protuberances[J]. Journal of Aircraft, 2011, 48(2): 591-600 [69]Favier J, Pinelli A, Piomelli U. Control of the separated flow around an airfoil using a wavy leading edge inspired by humpback whale flippers[J]. Comptes rendus-Mécanique, 2011, 340(1): 107-114 [70]Zhang M M, Wang G F, Xu J Z. Aerodynamic control of low-reynolds-number airfoil with leading-edge protuberances[J]. AIAA Journal, 2013, 51(8): 1960-1971 [71]Natarajan K, Sudhakar S, Paulpandian S. Experimental studies on the effect of leading edge tubercles on laminar separation bubble[C]//Aerospace Sciences Meeting. AIAA 2014-1279 [72]Hansen K, Kelso R, Doolan C. Reduction of flow induced tonal noise through leading edge tubercle modifications[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2010-3700 [73]Polacsek C, Reboul G, Clair V, et al. Turbulence-airfoil interaction noise reduction using wavy leading edge: An experimental and numerical study[C]//Inter-Noise and Noise-Con Congress and Conference, 2011 [74]Gruber M, Joseph P, Polacsek C, et al. Noise reduction using combined trailing edge and leading edge serrations in a tandem airfoil experiment[C]//18th AIAA/CEAS Aeroacoustics Conference, 2012 [75]Clair V, Polacsek C, Garrec T L, et al. Experimental and numerical investigation of turbulence-airfoil noise reduction using wavy edges[J]. AIAA Journal, 2013, 51(51): 2695-2713 [76]Narayanan S, Joseph P, Haeri S, et al. Noise reduction studies from the leading edge of serrated flat plates[C]//20th AIAA/CEAS Aeroacoustics Conference, 2014 [77]Narayanan S, Chaitanya P, Haeri S, et al. Airfoil noise reductions through leading edge serrations[J]. Physics of Fluids, 2015, 27(2): 1-17 [78]Chaitanya P, Narayanan S, Joseph P, et al. Leading edge serration geometries for significantly enhanced leading edge noise reductions[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2016-2736 [79]Haeri S, Kim J W, Narayanan S, et al. 3D calculations of aerofoil-turbulence interaction noise and the effect of wavy leading edges[C]//20th AIAA/CEAS Aeroacoustics Conference, 2014 [80]Turner J M, Wook K J. Aeroacoustic source mechanisms of a wavy leading edge undergoing vortical disturbances[J]. Journal of Fluid Mechanics, 2016, 811: 582-611 [81]Kim J W, Haeri S, Joseph P F. On the reduction of aerofoil-turbulence interaction noise associated with wavy leading edges[J]. Journal of Fluid Mechanics, 2016, 792: 526-552 [82]Aguilera F G, Gill J R, Angland D, et al. Wavy leading edge airfoils interacting with anisotropic turbulence[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2017-3370 [83]Mathews J, Peake N. Noise generation by turbulence interacting with an aerofoil with a serrated leading edge[C]//21st AIAA/CEAS Aeroacoustics Conference. Dallas, AIAA 2015-2204 [84]Lyu B, Azarpeyvand M, Sinayoko S. Noise prediction for serrated leading-edges[C]//22nd AIAA/CEAS Aeroacoustics Conference. Lyon, France, AIAA 2016-2740 [85]Chen W, Qiao W, Wang X, et al. An experimental and numerical investigation of airfoil instability noise with leading edge serrations[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2016-2956 [86]Mascha E. Uber die Schwungfedern[J]. Zeitschrift Fur Wissenschaftliche Zoologie, 1904, 77: 606-651. (in German)[87]Graham R R. The silent flight of owls[J]. Journal of the Royal Aeronautical Society, 1934, 38(286): 837-843 [88]Thorpe W H, Griffin D R. The lack of ultrasonic components in the flight noise of owls compared with other birds[J]. Ibis, 1962, 104(2): 256-257 [89]Kroeger R, Grushka H D, Helvey T C. Low speed aerodynamics for ultra-quiet flight[J]. University of Tennessee Space Institute, 1972. doi: 10. 1016/0022-460X(71)90105-2 [90]Gruschka H D, Borchers I U, Coble J G. Aerodynamic noise produced by a gliding owl[J]. Nature, 1971, 233(5319): 409-411 [91]Neuhaus W, Bretting H, Schweizer B. Morphologische und funktionelle Untersuchungen uber den ‘lautlosen’ Flug der Eulen (Strix aluco) im Vergleich zum Flug der Enten (Anas platyrhynchos)[J]. Biologisches Zentralblatt, 1973, 92: 495-51. (in German)[92]Geyer T, Sarradj E, Fritzsche C. Silent owl flight: experiments in the aeroacoustic wind tunnel[C]//Fortschritte der Akustik-NAG / DAGA, 2009 [93]Sarradj E, Fritzsche C, Geyer T. Silent owl flight: bird flyover noise measurements[J]. AIAA Journal, 2011, 49(4): 769-779 [94]Bachmann T, Klän S, Baumgartner W, et al. Morphometric characterisation of wing feathers of the barn owl Tyto alba pratincola and the pigeon Columba livia[J]. Frontiers in Zoology, 2007, 4(1): 1-15 [95]Kong D Y, Liang A P, Chu J K, et al. Study on mechanism of silent flight of owls[J]. Applied Physics, 2015, 5(11): 137-146. (in Chinese)孔德义, 梁爱萍, 褚金奎, 等. 猫头鹰的静音飞行机理研究[J]. 应用物理, 2015, 5(11): 137-146 [96]Lilley G M. A study of the silent flight of the owl[C]//4th AIAA/CEAS aeroacoustics conference. AIAA 1998-2340 [97]Brooks T F, Hodgson T H. Trailing edge noise prediction from measured surface pressures[J]. Journal of Sound & Vibration, 1981, 78(1): 69-117 [98]Ryi J, Choi J S. Noise reduction effect of airfoil and small-scale rotor using serration trailing edge in a wind tunnel test[J]. Science China Technological Sciences, 2017, B37: 1-8 [99]Fischer A, Bertagnolio F, Shen W Z, et al. Noise model for serrated trailing edges compared to wind tunnel measurements[J]. Journal of Physics: Conference Series, 2016, 753: 022053 [100]Hersh A S, Hayden R E. Aerodynamic sound radiation from lifting surfaces with and without leading edge serrations[R]. Washington: National Aeronautics and Space Administration. NASA CR-114370, 1971 [101]Hersh A S, Sodermant P T, Hayden R E. Investigation of acoustic effects of leading-edge serrations on airfoils[J]. Journal of Aircraft, 1974, 11(4): 197-202 [102]Arndt R E A, Nagel R T. Effect of leading edge serration on noise radiation from a model rotor[R]. AIAA 72-655, 1972 [103]Smith E G, Sowers H D. Cascade tests of serrated leading edge blading at high subsonic speeds[R]. NASA CR 2472, 1974 [104]Kopiev V, Zaitsev M, Belyaev I, et al. Noise reduction potential through slat hook serrations[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2011-2909 [105]Geyer T F, Wasala S H, Cater J E, et al. Experimental investigation of leading edge hook structures for wind turbine noise reduction[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2016-2954 [106]Chen W J, Wang X N, Qiao W Y, et al. Rod-airfoil interaction noise reduction using leading edge serrations[C]//21st AIAA/CEAS Aeroacoustics Conference. AIAA 2015-3264 [107]Longhouse R E. Vortex shedding noise of low tip speed, axial flow fans[J]. Journal of Sound & Vibration, 1977, 53(1): 25-46 [108]Lau A S H, Haeri S, Kim J W. The effect of wavy leading edges on aerofoil-gust interaction noise[C]//19th AIAA/CEAS Aeroacoustics Conference, 2013 [109]Lau A S H, Haeri S, Kim J W. The effect of wavy leading edges on aerofoil-gust interaction noise[J]. Journal of Sound & Vibration, 2013, 332(24): 6234-6253 [110]Chong T P, Vathylakis A, Mcewen A, et al. Aeroacoustic and aerodynamic performances of an aerofoil subjected to sinusoidal leading edges[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2015-2200 [111]Fish F E, Weber P W, Murray M M, et al. The tubercles on humpback whales’ flippers: application of bio-inspired technology[J]. Integrative & Comparative Biology, 2011, 51(1): 203-213 [112]Brooks T F, Pope D S, Marcolini M A. Airfoil self-noise and prediction[R]. NASA, 19890016302 [113]Mcalpine A, Nash E C, Lowson M V. On the generation of discrete frequency tones by the flow around an aerofoil[J]. Journal of Sound & Vibration, 1997, 222(5): 753-779 [114]Sandberg R D, Sandham N D, Joseph P F. Direct numerical simulations of trailing-edge noise generated by boundary-layer instabilities[J]. Journal of Sound & Vibration, 2007, 304(3- 5): 677-690 [115]Sandberg R D, Jones L E, Sandham N D, et al. Direct numerical simulations of tonal noise generated by laminar flow past airfoils[J]. Journal of Sound & Vibration, 2009, 320(4): 838-858 [116]Kingan M J, Pearse J R. Laminar boundary layer instability noise produced by an aerofoil[J]. Journal of Sound & Vibration, 2009, 322(4-5): 808-828 [117]Jones L E, Sandberg R D. Numerical analysis of tonal airfoil self-noise and acoustic feedback-loops[J]. Journal of Sound & Vibration, 2011, 330(25): 6137-6152 [118]Clair V, Polacsek C, Reboul G, et al. Numerical simulation of turbulence interaction noise applied to a serrated airfoil[C]//Proceedings of the Acoustics, 2012 [119]Roger M, Schram C, Santana L D. Reduction of airfoil turbulence-impingement noise by means of leading-edge serrations and/or porous material[C]//19th AIAA/CEAS Aeroacoustics Conference, 2013 [120]Turner J, Kim J W. Towards understanding aerofoils with wavy leading edges interacting with vortical disturbances[C]//AIAA/CEAS Aeroacoustics Conference. AIAA 2016-2952 [121]Lau A S H, Haeri S, Kim J W. The effect of wavy leading edges on aerofoil-gust interaction noise[J]. Journal of Sound & Vibration, 2013, 332(24): 6234-6253 [122]Chen W J, Qiao W Y, Tong F, et al. Experimental investigation of wavy leading edges on rod-airfoil interaction noise, Journal of Sound and Vibration. (in press)

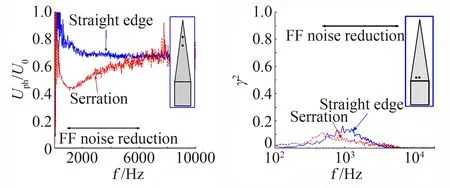

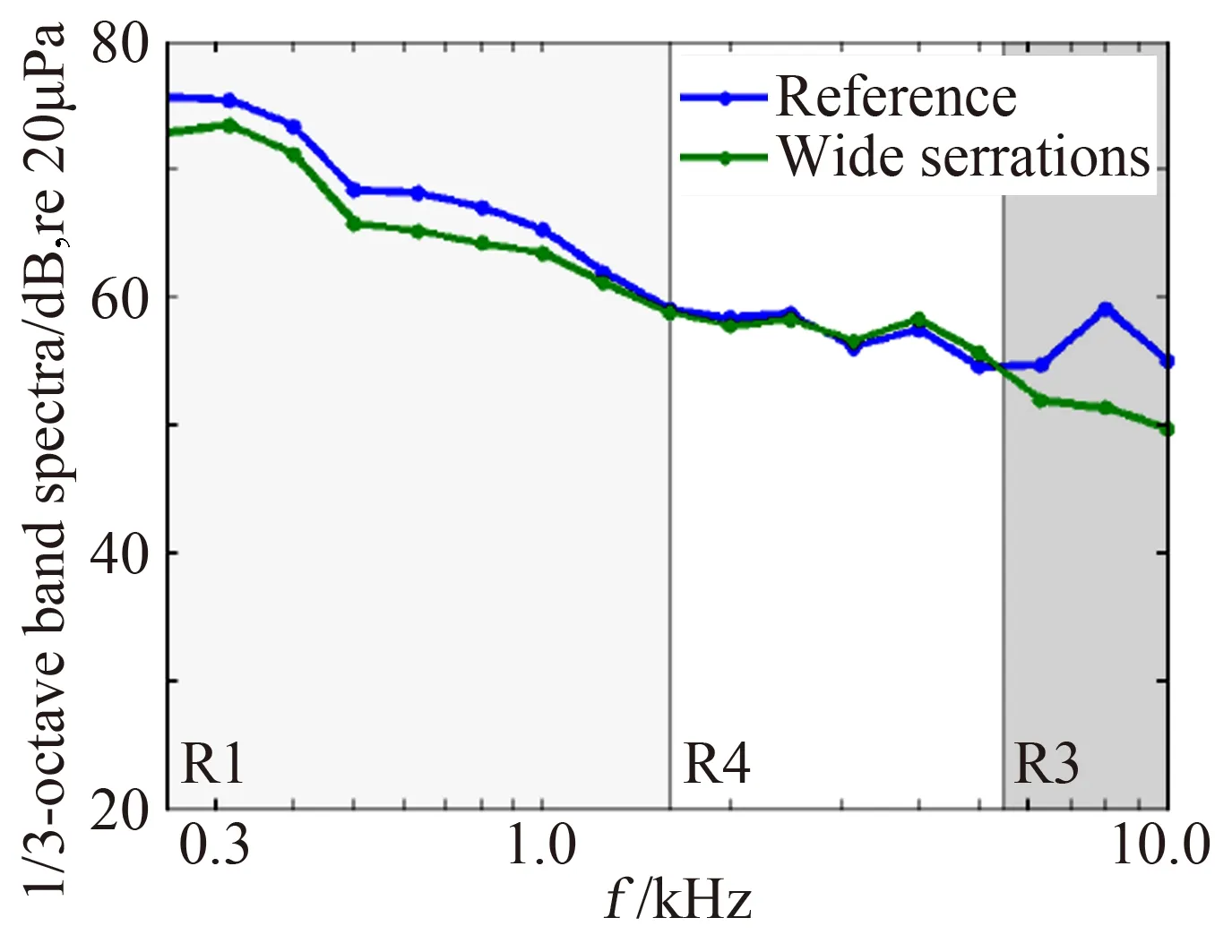

2.2 切开式尾缘锯齿降噪研究
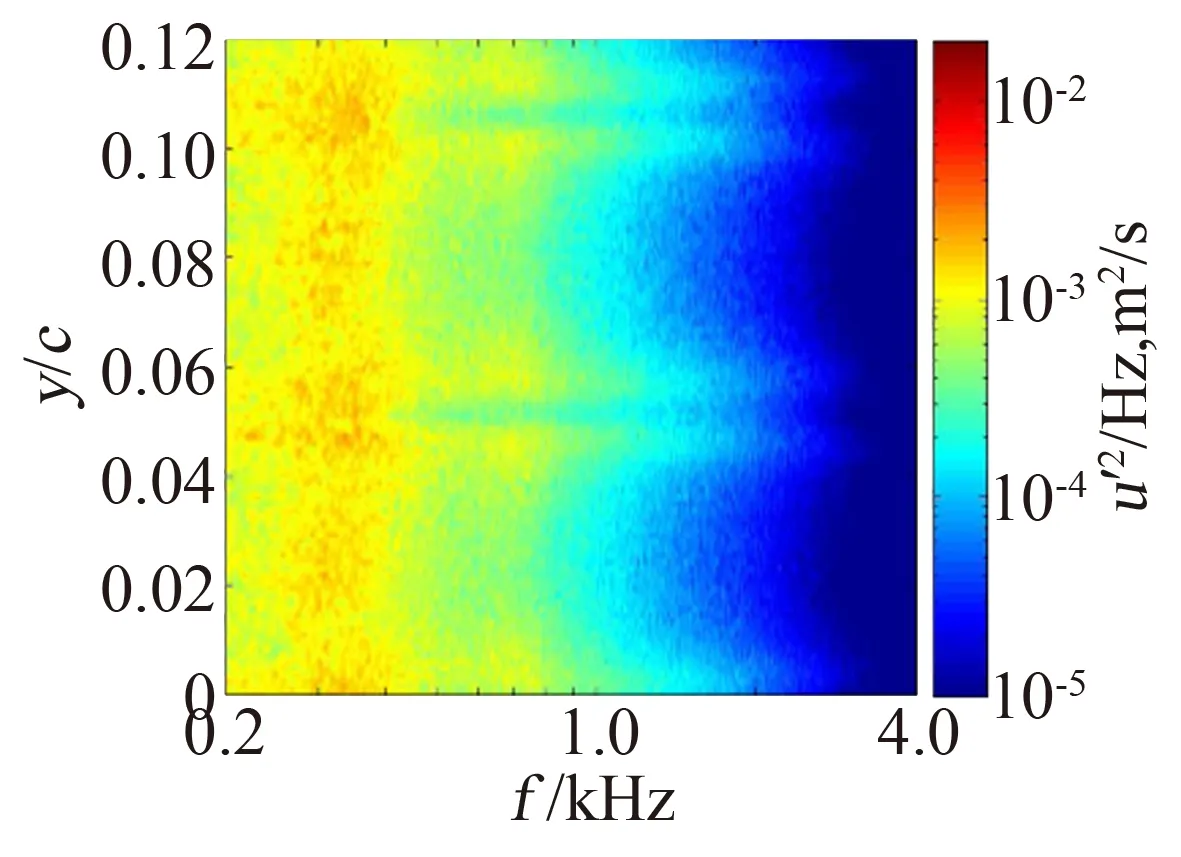
Fig.13Distributionofspectrumoffluctuationvelocityalongthespanwisedirection(1mmdownstreamoftheplate,y=0correspondstoserrationtiplocation)





2.3 真实叶片尾缘锯齿降噪研究

2.4 尾缘锯齿降噪流动与声学物理机制研究



3 机翼/叶片前缘仿生学降噪研究现状和发展动态





3.1 波浪形前缘对气动性能影响的研究




3.2 波浪形前缘对层流边界层不稳定噪声影响的研究



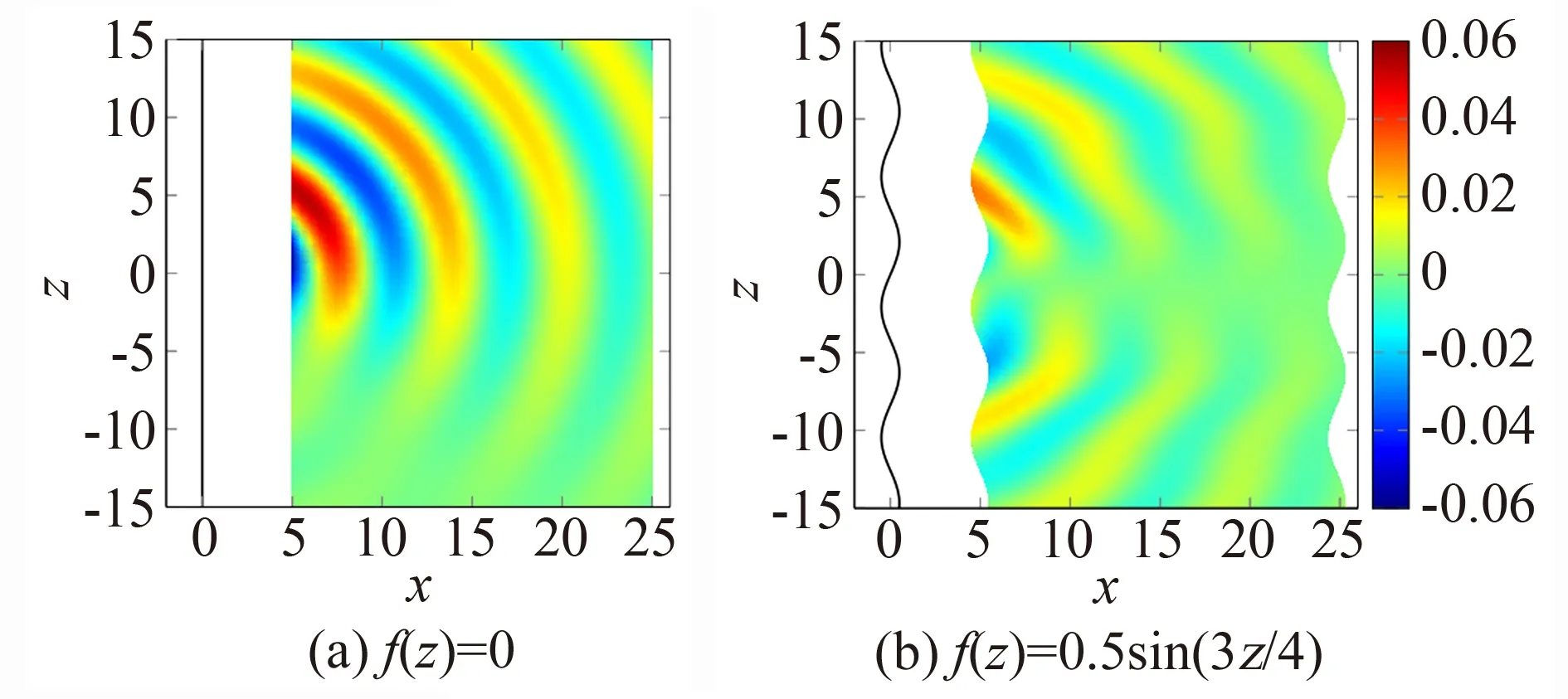
3.3 波浪形前缘对湍流干涉噪声影响的研究
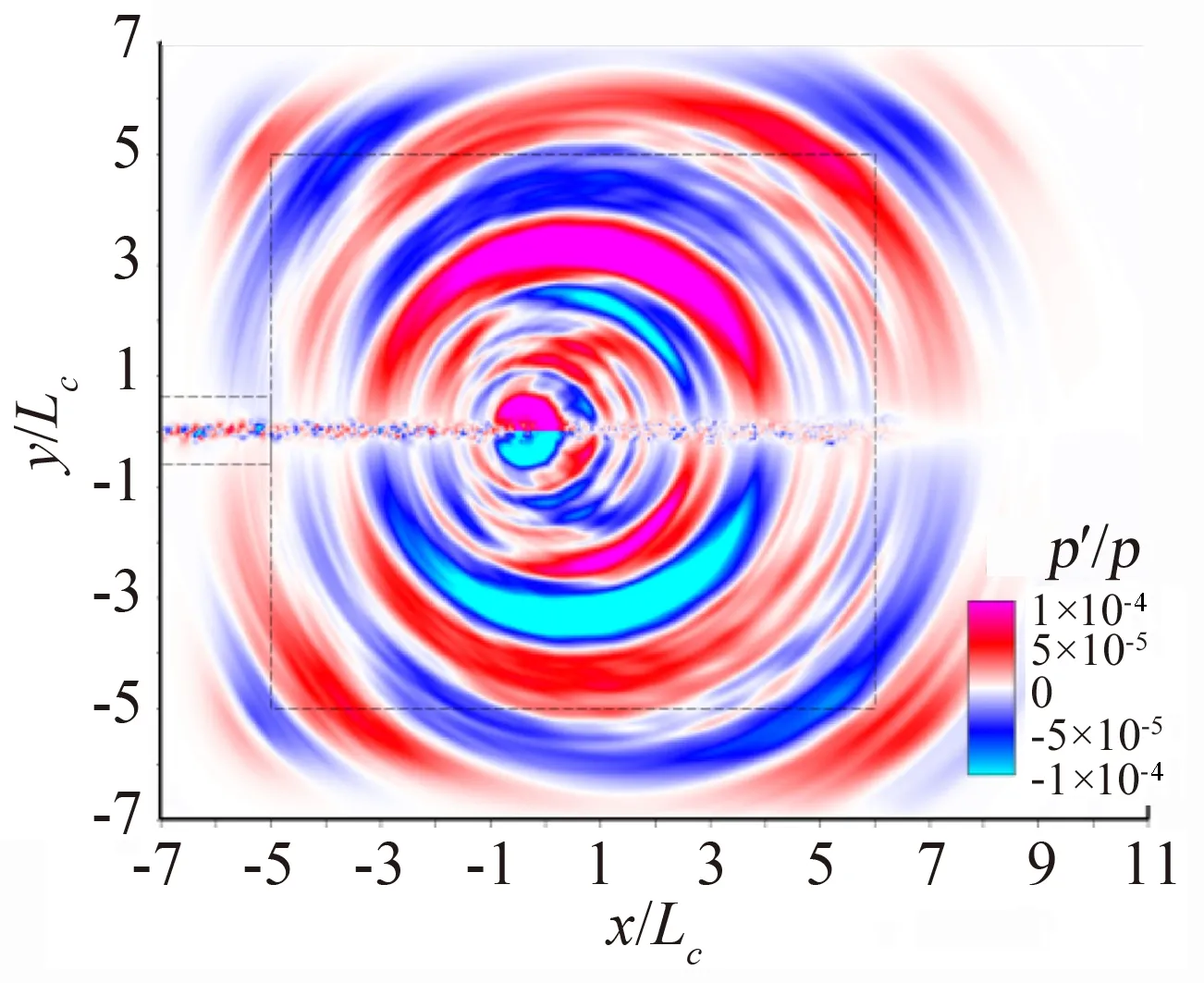
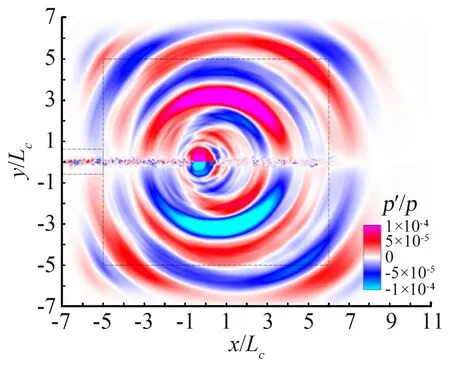


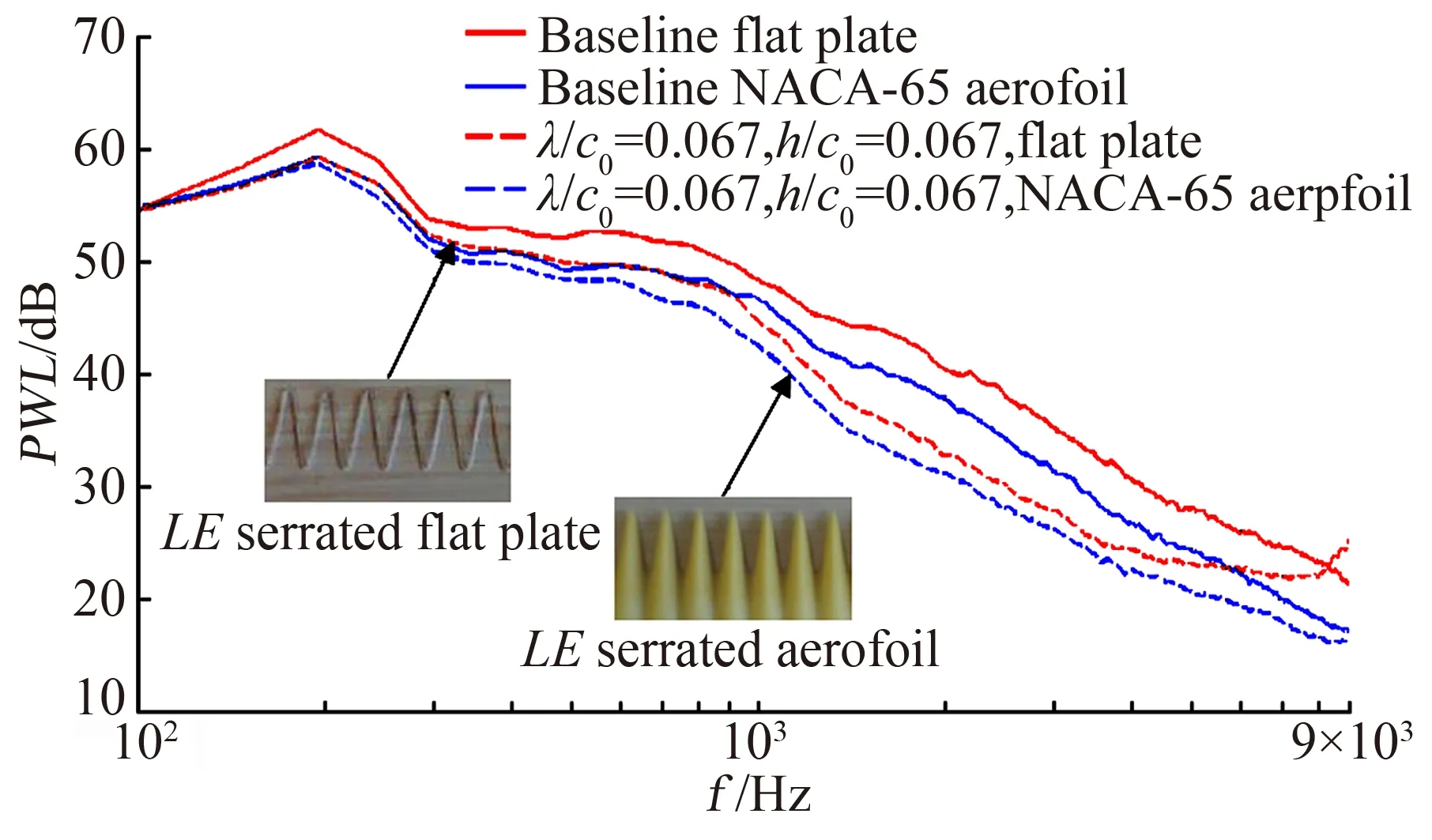
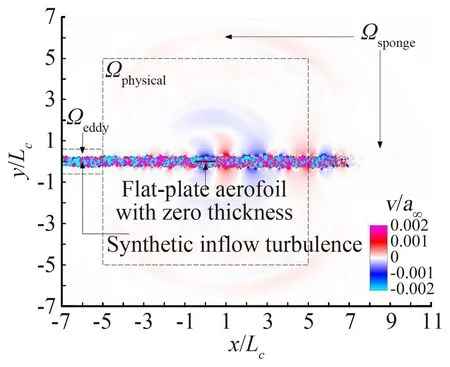






4 总 结
