跨声速风洞现代试验设计方法应用研究
2018-03-09曹军义张征宇黄叙辉中国空气动力研究与发展中心高速空气动力研究所四川绵阳6000西安交通大学机械学院陕西西安70049
李 多, 曹军义, 张征宇, 黄叙辉(. 中国空气动力研究与发展中心 高速空气动力研究所, 四川 绵阳 6000;. 西安交通大学 机械学院, 陕西 西安 70049)
0 引 言
目前,风洞试验主要采取传统的单变量方法(One Factor at a Time, OFAT)开展,其原理是在一次试验中选择一个自变量(如迎角)进行改变,并保持其它自变量不变,通过测量响应变量(如气动力和力矩),来得到自变量和响应变量的关系。但以美国为代表的航空航天发达国家发现,OFAT方法存在很多缺陷。例如一个自变量的改变必定会导致另外的自变量发生变化,如迎角在改变过程中会引起侧滑角的改变,这是OFAT风洞试验方法数据的误差来源之一[1]。同时,OFAT方法还存在忽略了试验中各变量间的交互作用、试验结果表示不直观以及需要采集的数据点较多而导致的试验成本高效率低等缺陷[2-4]。
1997年,美国航空航天局(NASA)兰利研究中心开始倡导使用现代试验设计方法(Modern Design of Experiment,MDOE)来代替OFAT方法。MDOE方法的原理是:每次试验中改变多个变量的值,同时考察多个变量与气动力、力矩间的关系,其核心是响应面法(Response Surface Method, RSM)。MDOE方法的优势是:1) 需要较少的数据点,成本低;2)提供了一个自变量影响响应变量的更全面的观察而不是普通数据图的表示方法:响应仅是一个自变量的函数,其余变量被固定在定值;3) 能给出除物理设置外的各自变量的响应值;4) 不仅能精确估计出设计空间某个特定点上的响应值,同时还能给出该响应值的不确定度,从而显著减小试验结果的不确定度;5) 能够很好的表示出变量之间的交互作用;6) 不需要知道响应曲面的具体数学形式[5]。
本文在我国2.4 m跨声速风洞中开展了MDOE试验,研究试验中涉及的试验区间确定、子区间划分、数据点数量选取、数据点在子区间的分布等具体问题,验证MDOE方法在降低试验成本、优化试验结果表达、体现变量间交互作用等方面的优势。
1 试验设计
选择迎角a和侧滑角β为两个自变量,阻力系数CD为相应的响应变量,试验区间为迎角-4°~8°,侧滑角-5°~5°。由于变量的个数为2,试验区间可以表示成一个笛卡尔坐标系的平面,其中x轴代表迎角,y轴代表侧滑角,区间中每个数据点表示迎角与侧滑角的不同组合。
1.1 子区间划分
为了避免响应面模型中增加高阶项,必须将试验区间划分为不同的子区间,最后通过整合所有的毗邻的变量子区间,就能够得到一个精确且连续的响应面方程[6]。考虑到正负区间的不对称因素及大迎角范围非线性严重的特点,将迎角区间划分为3个子区间,如图1及表1所示。

图1 子区间划分Fig.1 Subspace divide

表1 子区间划分Table 1 Subspace divide
1.2 数据量确定
数据点的个数决定了模型的精度与所采取方法的效率,必须精确计算。Box和Draper给出了一个计算每个子区间试验点数n的方程[7]:

(1)
式中,ta代表置信区间的半宽,查统计手册为1.96,γ为试验精度,取0.0001,p代表回归模型中参数的个数等于6,σ为数据标准差,以精度最高的滚转力矩为例,其标准差不大于0.00007,代入式(1)中可求得:

(2)
因此在本试验中,每个子区间指定12个数据点,共需要36个数据点。
1.3 数据点分布
在各子区间内,数据点的分布方式不同导致方差不同。本文采用中心复合试验设计方法(central composite design, CCD)分布各子区间的试验点[8],其中独立变量经过线性编码按-1、1来进行分布。式(3)说明了转换过程[9]。

(3)
图2表示了编码CCD方法中点的分布,除了四个拐点与星点外,重复性被指定在设计中心来抑制预测方差,由于每个子区间内有12个数据点,所以在设计中心重复点的数量是4。
12个数据点为每个子区间提供12个自由度,其在子区间内的分配方法如表2所示。

图2 数据点分布Fig.2 Data points distribution

表2 自由度分配Table 2 Degree of freedom distribution
1.4 试验设计总结
图3显示了36个数据点在试验区间的分布,共有29个点,其中三个点重复了4次,两个点重复了2次,其中重复2次的数据点用来确保各子区间响应面模型的独立性。

图3 数据点在试验区间分布Fig.3 Data points distribution in experiment space
2 试验数据处理
2.1 响应面模型建立
开展风洞试验获取36个数据点上的气动系数后,建立了阻力系数CD的响应面模型,如图4所示。
从图4的响应面模型中看出:采用MDOE试验方法后,每个子区间内仅需12个数据点就能得到气动系数的响应值,而OFAT方法则需要45个数据点,试验结束后耗气量结果对比显示,MDOE方法的耗气量仅占OFAT方法的50%,降低了成本;MDOE风洞试验方法提供了一个迎角和侧滑角影响各气动系数的更全面的观察而不是普通数据图的表示方法:响应仅是迎角的函数,侧滑角被固定在定值;MDOE试验方法打破了单变量方法侧滑角被物理固定在整数角度(2°、4°、6°等)的局限性,给出了整个设计区间的响应值,在设计区间内,迎角和侧滑角可以以任意小数角度进行组合;最后,MDOE试验方法很好的表示出了两个变量迎角和侧滑角之间的交互作用,以图4(a)为例,若想减小阻力系数CD,在只减小迎角的情况下CD变化不明显,但如果在减小迎角的同时增大侧滑角,则CD的值会急剧下降。
气动系数在各子空间内响应面模型的多项式构成如表3所示,多项式构成中包含的项用“√”标出。

(a) -4°~0°

(b) 0°~4°
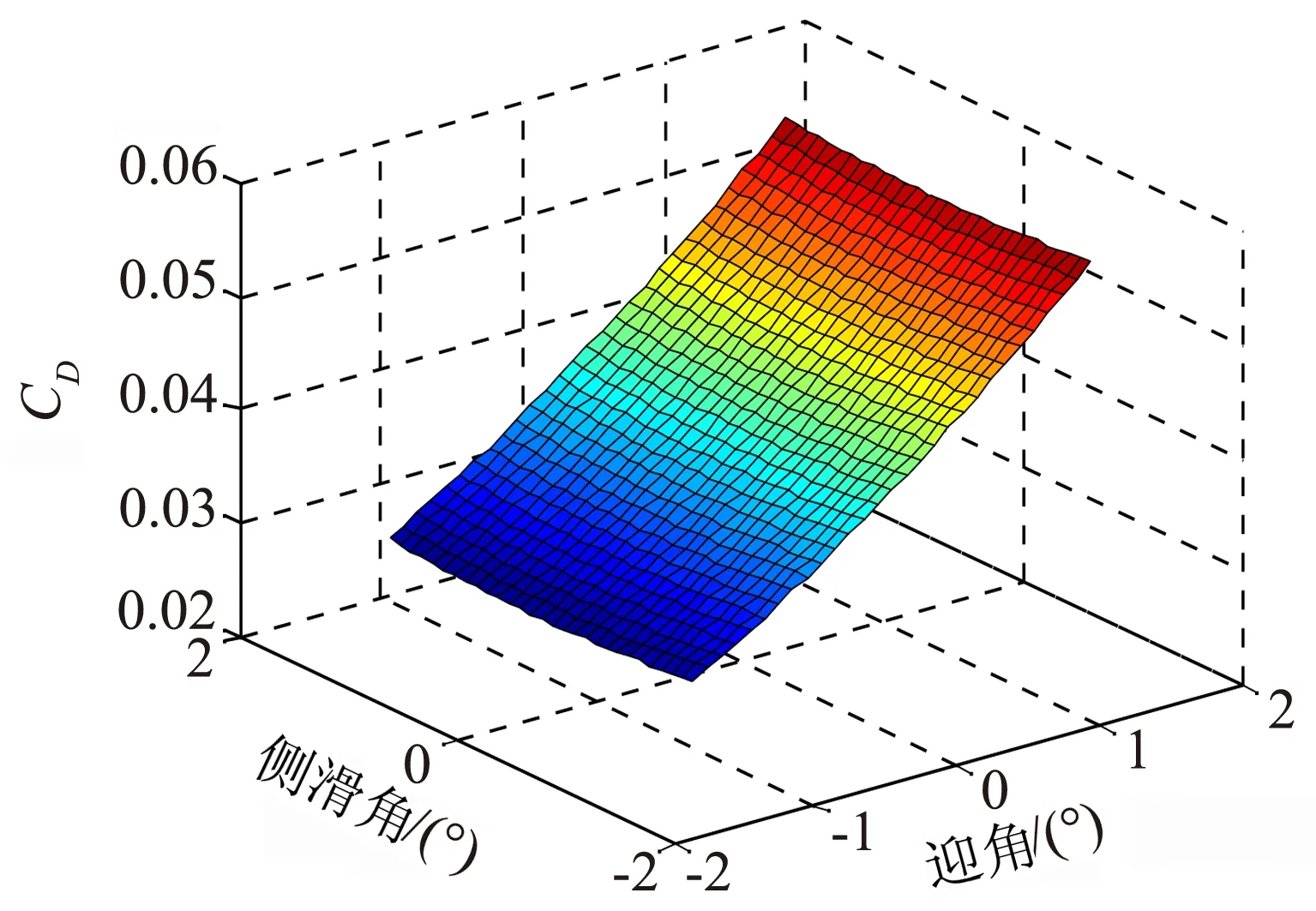
(c) 4°~8°

表3 响应面多项式构成Table 3 Polynomial composition of response surface
2.2 方差分析
以0~4°迎角范围内阻力系数CD为例,说明响应面回归的过程,方差分析表如表4所示[10]。
首先观察ANOVA表中的总效果,对应回归项的P值为0.000(即<0.001),表明本模型总的来说是有效的,对应失拟项的P值为0.512,其值远比临界值0.05大,即表明本模型没有失拟现象。
最后观察各项效应的显著性,可以看出迎角、迎角*迎角、侧滑角*侧滑角三项高度显著,而侧滑角、迎角*侧滑角两项不显著(P值>0.05),应将其删除。
从改进后的方差分析表5中可以看出,各项效应均为显著,同时与全模型方差分析表中的数据相比R-Sq(调整)的值略有上升而s的值略有下降,数据表明改进后的模型比原模型更准确。

表4 方差分析Table 4 Analysis of variance
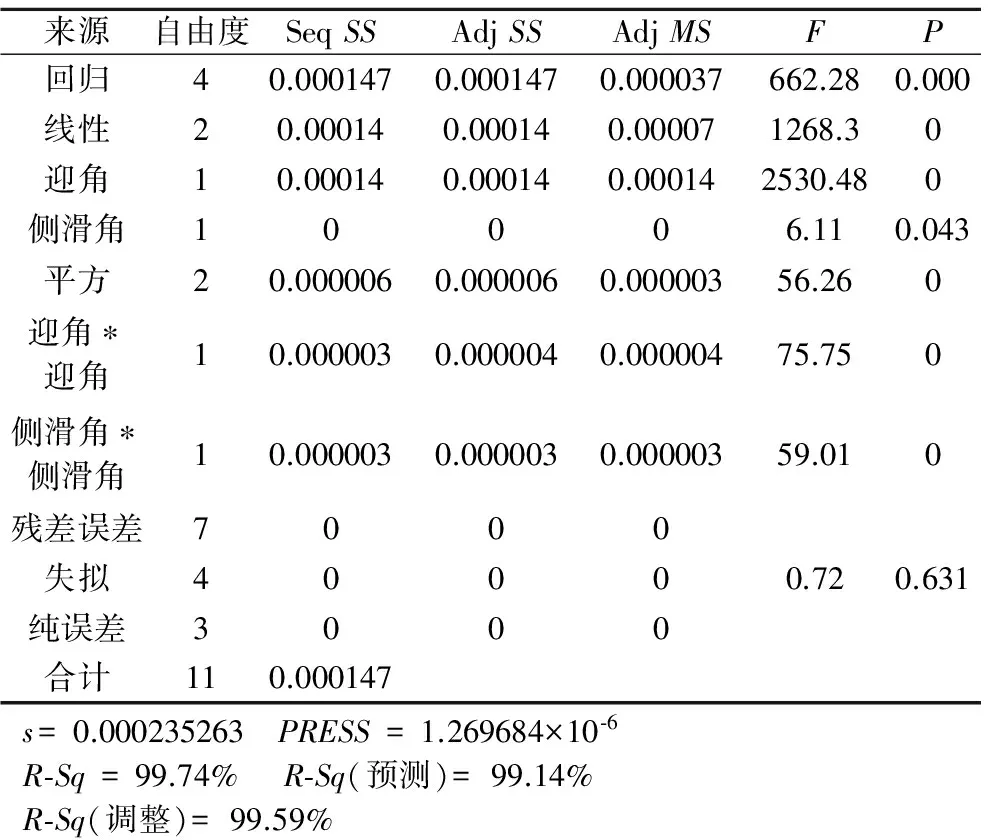
表5 方差分析改进Table 5 Secondary analysis of variance
2.3 模型验证
为了验证所建立响应面模型的准确性,在每个子区间β=0°的曲线上选取5个额外的试验点检验其是否能够落在拟合曲线的95%置信区间内,检验结果如图5所示,其中蓝色曲线代表上下置信区间,黑色曲线代表本试验拟合曲线,红色点代表检验点。
从图5中看出,在每个子区间内,中间范围的点检验结果较好,而边界地区的点检验结果较差,也反映了中心复合设计方法在中心区域误差较小而边界处误差较大的特点。但基本上所有的点都能落入95%置信区间内,说明响应面模型精度足够。

(a) -4°~0°

(b) 0°~4°

(c) 4°~8°
3 结 论
通过本次试验的开展,主要得到以下结论:
1) 对比得出,MDOE风洞试验方法仅需传统单变量试验方法20%的测量数据量即可完成试验,所需的吹风时间约占传统单变量试验方法的50%,同时在试验结果表达、更多响应值的提供、不确定度估计、交互作用体现等方面较单变量方法更有优势;
2) 方差分析结果表明,迎角对气动系数的影响比侧滑角更为显著,正确反映了该类飞行器的气动特性变化规律;
3) MDOE风洞试验方法能够以气动系数响应面模型和方差分析表的形式提供更为详细、全面的风洞试验数据,在飞行器风洞试验的方案设计及数据分析中具有较为广阔的应用前景。
[1]张江, 秦永明, 马汉东. 亚跨超风洞现代试验设计方法研究[J]. 空气动力学学报, 2015, 33(3): 384-391
[2]战培国. MDOE风洞试验方法研究[J]. 航空科学技术, 2011(6): 11-14
[3]张江, 秦永明, 马汉东. 风洞 MDOE 的形式实验设计方法研究[J]. 空气动力学学报, 2016, 34(1): 59-69
[4]唐志共, 王文正, 陈功, 等. 气动模型在现代气动试验设计中的应用研究[J]. 空气动力学学报, 2017, 35(2): 172-176
[5]Kaymaz I, McMahon C A. A response surface method based on weighted regression for structural reliability analysis[J]. Probabilistic Engineering Mechanics, 2005, 20(1): 11-17
[6]Garrent J H. Where and why article neural networks are applicable in civil engineering[J]. Journal of Computing in Civil Engineering, ASCE, 1994, 8(2): 129-130
[7]Erickson G E. Analysis of a split-plot experimental design applied to a low-speed wind tunnel investigation[R]. NASA/TM-20130218013
[8]De Loach R. Applications of modern experiment design to wind tunnel testing at NASA langley research center[C]//36thAIAA Aerospace Sciences Meeting&Exhibit, Reno, Nevada, January 1998, AIAA-1998-0713
[9]Landman D, Simpson J, Vicroy D, et al. Efficient methods for complex aircraft configuration aerodynamic characterization using response surface methodologies[C]//44thAIAA Aerospace Sciences Meeting & Exhibit, Reno, Nevada, January 2006, AIAA-2006-0922
[10]马逢时, 周暐. 六西格玛管理统计指南: MINITAB使用指导[M]. 北京: 中国人民大学出版社, 2013.
