基于自适应积分滑模的舰载机纵向航迹最优控制
2018-03-08陈志刚陈俊锋
陈志刚,韩 维,张 勇,陈俊锋
(1.海军航空工程学院 飞行器工程系,山东 烟台 264001; 2.海军装备研究院,上海 200436)
0 引言
固定翼舰载机在进舰着舰过程中要求严格按预定的下滑轨迹飞行,以提高着舰成功率,保证着舰安全。着舰过程中,影响舰载机安全着舰的主要因素包括航母的六自由度运动和舰尾流干扰。航母的运动会导致舰载机的理想着舰点产生较大偏差,舰尾流干扰使得舰载机的着舰下滑轨迹偏离理想轨迹。舰载机着舰失败和着舰事故大多数是由纵向航迹控制性能不好造成的。因此,纵向航迹控制在舰载机着舰控制系统中具有重要作用。
文献[1]以F-18舰载机为对象,研究了以PID控制器为核心的纵向着舰引导控制律。文献[2-3]通过引入模糊控制对传统的PID着舰引导控制律进行改进,实现了控制器参数在线最优调节,提高了航迹控制精度。现代控制方法也被广泛用于飞行航迹控制中,如最优控制、滑模控制、自适应控制等。线性二次型调节器(LQR)是基于线性系统的最优控制方法,被大量应用于飞机的飞行控制[4-6]。文献[7]提出一种新的积分滑模控制与自适应模糊相结合的控制律用于无人机着舰飞行控制,具有较好的控制精度和鲁棒性。文献[8]将自适应控制和模糊参数整定结合,构建了舰载机着舰的航迹控制系统。文献[9]提出了一种基于非线性动态逆的滑模控制方法,并用于舰载机纵向着舰飞行控制系统,达到了很高的着舰航迹控制精度。
本文通过分析舰载机着舰纵向运动模型,基于LQR和自适应积分滑模控制方法设计舰载机自动着舰纵向航迹控制律,并计算分析初始高度误差和甲板运动对航迹控制的影响。
1 舰载机纵向着舰模型
1.1 舰载机运动模型
舰载机在进舰着舰过程中按一定的下滑角保持匀速直线运动,其纵向动力学和运动学方程组用线性小扰动状态方程[10]表示为:

(1)
其中:v为速度扰动量,V*为舰载机着舰过程中的基准飞行速度,α为迎角扰动量,θ为俯仰角扰动量,q为俯仰角速度扰动量,h为高度扰动量,γ为航迹角扰动量,δe为升降舵偏角,δT为推力变化量。
1.2 航母运动模型
在舰载机着舰过程中,航空母舰沿着斜角甲板中心线方向匀速前进。但由于海面上的风、海浪等因素的影响,航空母舰还会进行复杂的摇晃运动。因此,航空母舰在海面上的运动是六自由度运动。其中,理想着舰点的高度变化主要受航空母舰的纵摇和垂荡运动的影响。
在工程实践中,航空母舰的海上运动可以用谐波形式的振荡来近似表示,如公式(2)所示,而运动的随机性则用随机相位来描述。
(2)
式中,Θ和Z分别表示纵摇运动(°)和垂荡运动(m),AΘ和AZ分别表示纵摇运动和垂荡运动的幅值,ωΘ和ωZ分别表示纵摇运动和垂荡运动的角速度,φΘ和φZ分别表示纵摇运动和垂荡运动的随机相位。
理想着舰点的高度变化为:
dh=Z+Θ·LTD
(3)
式中,LTD表示航母纵摇中心与理想着舰点的距离。
1.3 舰尾流模型
舰载机着舰过程中,舰尾流对飞行姿态和着舰精度会产生很大的扰动。根据美军标MIL-HDBK-1797中的工程化模型,舰尾流由自由大气紊流分量、尾流稳态分量、尾流周期分量和尾流随机分量组成。
2 纵向航迹控制律设计
舰载机自动着舰系统[1,10]中,通过测量舰载机在惯性测量系统中的高度,与理想下滑轨迹相比较,得到着舰高度偏差,经航迹控制律计算给出飞行姿态角指令并发送给舰载机。通过飞行控制系统(AFCS)来控制舰载机飞行姿态以跟踪飞行姿态角指令,使舰载机飞行高度不断跟踪理想下滑轨迹,完成对飞行高度的纠偏。同时通过进场动力补偿系统(APCS)来控制舰载机的推力大小,使舰载机在低动压飞行状态下能快速准确地调整飞行迎角并保持恒定。在舰载机着舰前13s左右,在着舰航迹控制律中引入甲板运动信号,使得舰载机在着舰的最后阶段实时跟踪理想着舰点,保证着舰精度。在着舰过程中,舰载机受到舰尾流的持续干扰,航迹控制律应实现抗舰尾流干扰的功能。
舰载机纵向着舰控制系统如图1所示。在自动着舰控制律中,AFCS和APCS分别采用自抗扰控制(ADRC)方法进行设计。
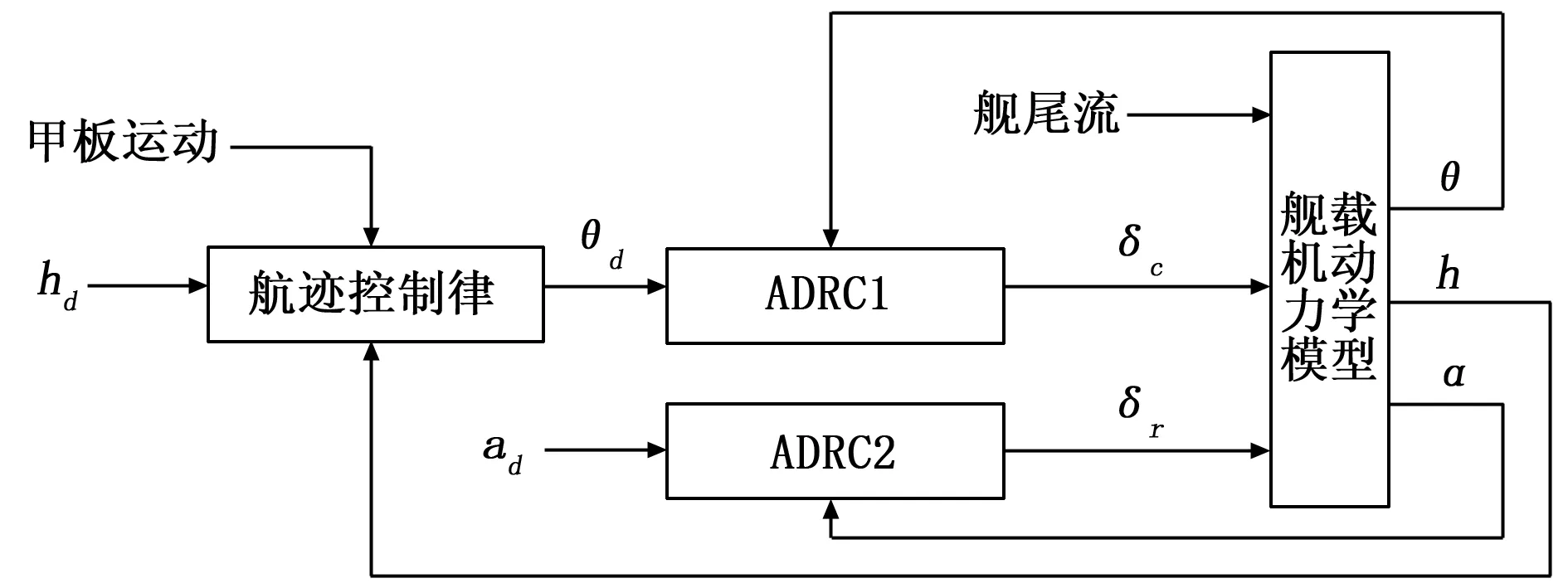
图1 系统设计框图
2.1 纵向航迹运动模型
舰载机进舰着舰过程中,高度变化率与航迹角及飞行姿态角之间有如下关系[10]:
(3)
若理想高度为hd,舰载机高度误差为:
e=h-hd
舰载机着舰纵向航迹控制律的主要目的是通过控制俯仰角θ来消除高度误差,使高度误差e在有限时间内趋于0。令控制量u=θ,则:
(4)
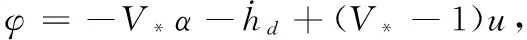

(5)

对式(5)的系统,将控制量u分为u0和u1两部分,即u=u0+u1,其中u0是标称控制量,用来控制系统(5)的标称模型,u1用来抵消不确定项φ对标称模型的影响。
2.2 线性二次型最优控制
先考虑系统(3)的标称模型,即:
(6)
对标称模型(6),采用线性二次型调节器(LQR)[11]可使e在有限时间t=tf<∞内收敛到e=0的任意小邻域内。
控制量u0应使下述二次型积分代价函数最小:
(7)
式中,Ptf≥0,Q≥0,R>0。
对系统(6),LQR控制器可设计为:
(8)
式中,P(tf)=Ptf,P(t)是满足如下Riccati微分方程的解:
(9)
2.3 自适应积分滑模控制
为了抵消不确定项φ对标称模型的影响,使系统(6)能够在控制律(8)的作用下在有限时间t=tf<∞内收敛到e=0的任意小邻域内,采用积分滑模控制[12],定义滑模面如下:
s=e+ξ
(10)
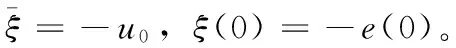
对式(10)取微分,可得:
(11)
为使t≥0时,s=0一直成立,可设计如下控制律:
u1=-ksign(s)
(12)
式中,k的取值范围由定理1给出。
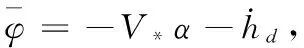
证明:取Lyapunov函数:
(13)
对式(13)求导可得:
|s|[C+(V*-1)u0M-V*k]≤-|s|η≤0
(14)
式(14)证明了当存在不确定项时,滑模面s=0也是可达的,且由于s(0)=0,保证了t≥0时,s=0一直成立。

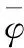
(15)

(16)
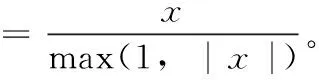
3 仿真计算
仿真计算以某舰载机[15-16]为算例飞机,考虑中等海况下的甲板运动,舰尾流采用美军标MIL-HDBK-1797中所描述的舰尾流工程化模型[17]。舰载机基准着舰速度为67.3m/s,下滑角为3.5°。
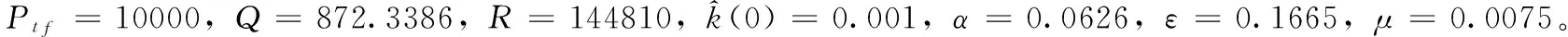
图2~图4是初始高度误差分别为0m,-10m和-20m时在本文航迹控制律作用下舰载机实际航迹和理想航迹的对比曲线。
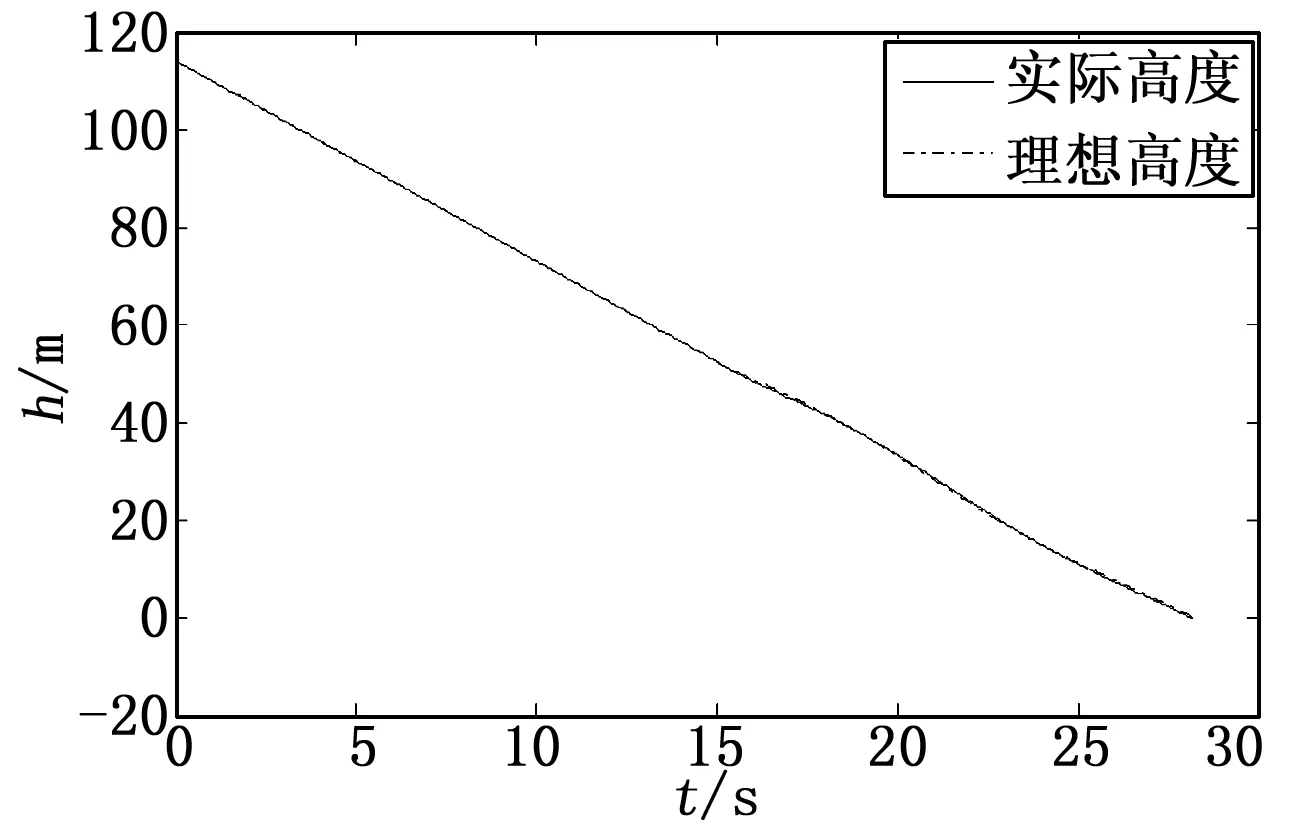
图2 初始误差为0 m时舰载机实际高度和理想高度曲线
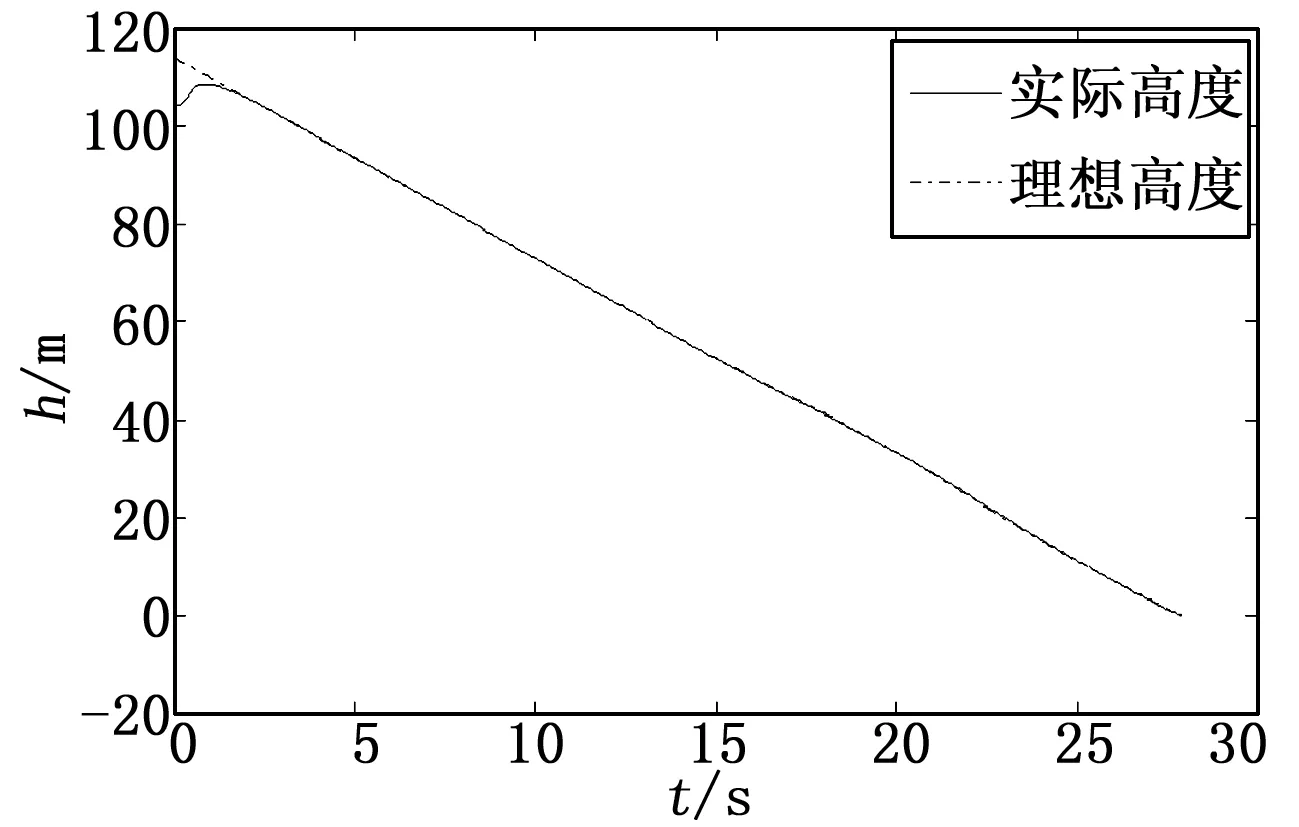
图3 初始误差为-10 m时舰载机实际高度和理想高度曲线
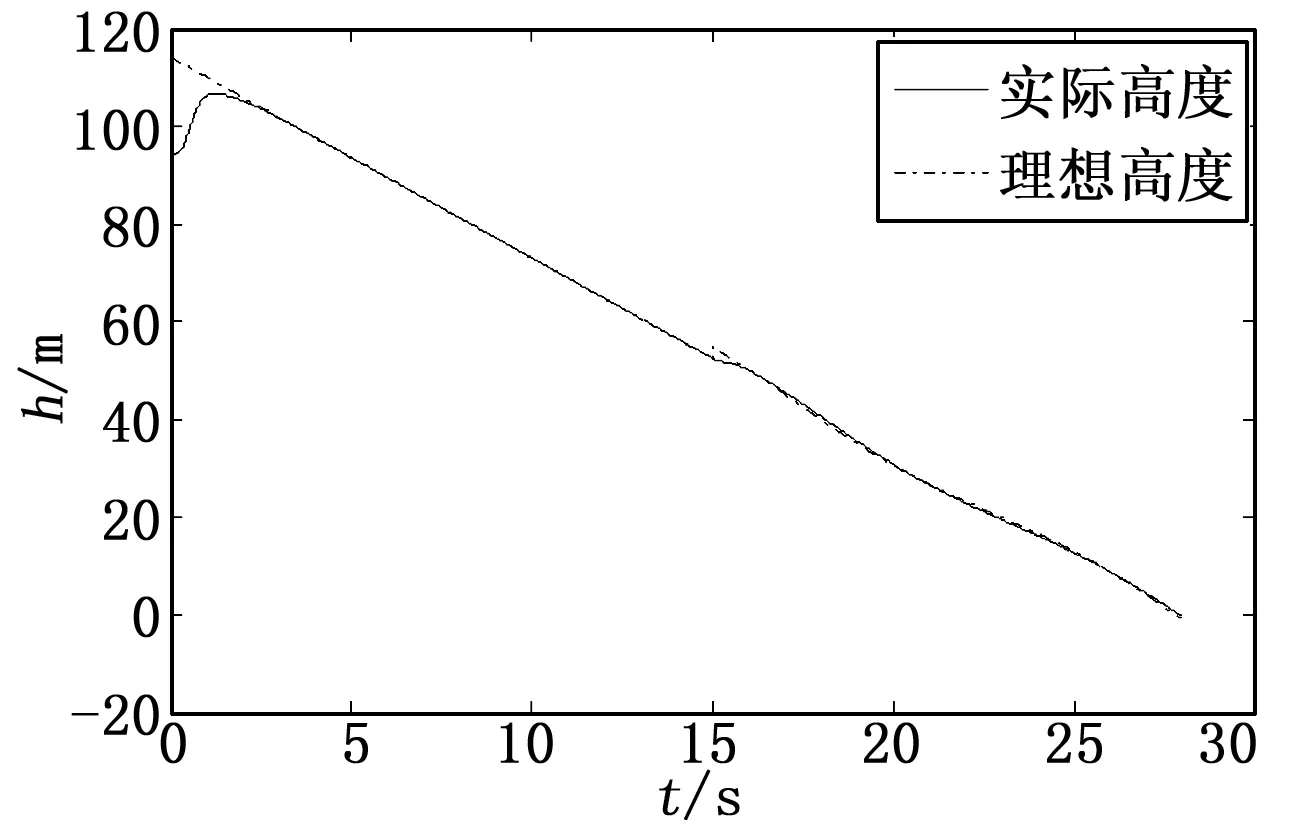
图4 初始误差为-20 m时舰载机实际高度和理想高度曲线
由图2~图4可知,不同的初始高度误差下,舰载机能快速完成航迹纠偏。着舰过程中,舰载机下滑轨迹基本没有受到舰尾流的干扰。着舰前13s时,由于引入甲板运动信息,理想着舰轨迹发生变化,航迹控制律能够使舰载机实际下滑轨迹很好地跟踪理想轨迹,从而保证着舰成功。
4 结论
本文结合自适应积分滑模和LQR设计了舰载机自动着舰的纵向航迹控制律,以实现着舰轨迹的精确控制。仿真结果表明,所设计的纵向航迹控制律不仅可以消除舰尾流扰动和航母甲板随机运动的影响,而且可以实现航迹偏差的修正,使舰载机能够严格按照理想下滑轨迹着舰。
[1] 彭 兢.舰载飞机进舰着舰的自动引导和控制研究[D].北京:北京航空航天大学, 2001.
[2] 彭秀艳,王志文,吴 鑫.舰载机纵向自动着舰控制[J].智能系统学报,2011,6(2):172-177.
[3] 邓 娟,颜振萍,艾剑良.模糊控制技术在自动着舰控制系统中的应用[J].系统仿真学报,2012,24(3):645-650.
[4]SubramanianRG,ElumalaiV.RobustMARCaugmentedbaselineLQRfortrackingcontrolof2DoFhelicopter[J].RoboticsandAutonomousSystems, 2016, 86: 70-77.
[5]ZhiYF,LiGS,SongQ,etal.FlightcontrollawofunmannedvehiclesbasedonrobustservolinearquadraticregulatorandKalmanfiltering[J].InternationalJournalofAdvancedRoboticSystems, 2017, 14(1):1-7.
[6]ChrifL,KaddaZM.AircraftcontrolsystemusingLQGandLQRcontrollerwithoptimalestimation-Kalmanfilterdesign[J].ProcediaEngineering, 2014, 80: 245-257.
[7] 郑峰婴,龚华军,甄子洋.基于积分滑模控制的无人机自动着舰系统[J].系统工程与电子技术,2015,37(7):1621-1628.
[8] 焦 鑫,江 驹,王新华,等.基于模型参考模糊自适应的舰尾流抑制方法[J].南京航空航天大学学报,2013,45(3):396-401.
[9] 朱齐丹,孟 雪,张 智. 基于非线性动态逆滑模的纵向着舰系统设计[J].系统工程与电子技术,2014,36(10):2037-2042.
[10] 杨一栋,余俊雅.舰载飞机着舰引导与控制[M].北京:国防工业出版社,2007.
[11] 张洪钺,王 青.最优控制理论与应用[M].北京:高等教育出版社,2006.
[12]UtkinV,ShiJ.Integralslidingmodeinsystemsoperatingunderuncertainty[A].Proc.ofthe35thConf.DecisionandControl[C].Kobe,Japan, 1996: 4591-4596.
[13]HarmoucheM,LaghroucheS,ChitourY.Robustandadaptivehigherorderslidingmodecontrollers[A].Proc.ofthe51stConf.DecisionandControl[C].MauiHawaii,USA, 2012: 6436-6441.
[14]WangL,ShengYZ,LiuXD.Anoveladaptivehigh-orderslidingmodecontrolbasedonintegralslidingmode[J].InternationalJournalofControl,Automation,andSystems, 2014, 12(3): 459-472.
[15] 满翠芳.舰载机自动着舰控制技术研究[D].南京:南京航空航天大学,2010.
[16] 陈俊锋,韩 维,胡洋.基于高阶滑模的舰载机着舰动力补偿系统仿真[J].飞行力学,2015,33(1):26-29.
[17] 崔 玫. 舰载机全自动着舰引导飞控系统设计[D]. 哈尔滨:哈尔滨工程大学, 2013.
[18] 符 曦.系统最优化及控制[M].北京:机械工业出版社,1995.
