基于定子电阻自适应的MRAS系统对比研究
2018-03-07李坤蒋林杨俊翔刘康宁
李坤,蒋林,杨俊翔,刘康宁
( 西南石油大学电气信息学院,四川 成都 635029 )
0 引言
无速度传感器控制是交流调速系统的一个研究热点,大量的无速度传感器控制方法可运用于矢量控制系统,这些控制方法各具特点和适用范围。其中,模型参考自适应法因其原理简单、易于实现且具有较好的鲁棒性,具备较好的研究价值。本文结合相关文献推导三种MRAS系统各自的参考模型和可调模型,以此构成矢量控制系统。基于电机内部变量的稳态关系,绘制出转速误差与实际转速、负载的三维关系图,分析辨识转速对电机定子电阻的敏感性。基于MATLAB仿真平台,对三种转速辨识的MRAS系统工作在低速状态时,系统对于定子电阻变化的鲁棒性做了仿真对比分析。
1 概述
传统的模型参考自适应系统(MRAS)以电压模型作为参考模型,电流模型作为可调模型进行转速辨识。电压模型中含有纯积分环节和定子电阻。积分环节使得系统存在积分初值和直流偏移的问题。采用新的积分策略和选择不含积分环节的参考模型均可以解决纯积分环节带来的影响。文献[4]提出,用一阶滤波器环节代替纯积分环节,并设计相应的补偿环节来补偿由滤波器造成的幅值和相位误差,但该方法只能抑制不能消除直流分量误差。文献[5]提出了以反电动势作为输出量的MRAS系统,该方法消除了参考模型中的纯积分环节,改善了系统的控制性能,但参考模型仍含有定子电阻,系统存在对定子电阻鲁棒性差和低速性能较差的问题。文献[6-7]将电机转速和定子电阻作为时变参数,通过在线辨识电机的定子电阻,进而减小定子电阻变化对系统的影响,提高系统的转速辨识精度。文献[8]提出了一种基于瞬时无功功率的MRAS系统,该方法去掉了定子电阻带来的影响,对定子电阻有较好的鲁棒性,系统能获得较好的转速辨识精度。文献[9]提出以异步电机本身作为参考模型的基于定子电流MRAS系统来辨识电机的转速,该系统同样避免了定子电阻的存在,不含积分运算和电势的计算,系统能够获得良好的低速性能。上述文献均未对基于转子磁链、无功功率和定子电流三种MRAS系统对定子电阻鲁棒性做系统的理论分析和对比仿真验证。
2 异步电机数学模型
异步电机在αβ坐标系下的动态数学模型为:
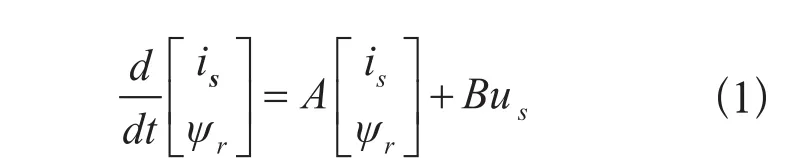
式中:us、is分别为定子电压、电流矢量,ψr为转子磁链矢量,其中
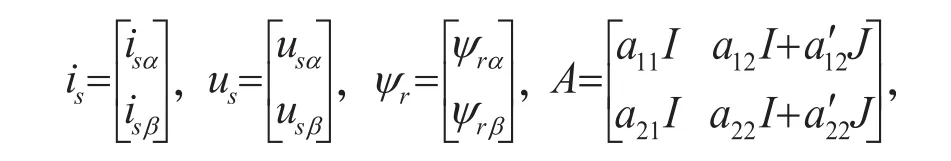

3 模型参考自适应系统
模型参考自适应系统主要由转速辨识机构、参考模型和可调模型三部分组成。其转速辨识原理为:估算转速反馈到含有转速变量的可调模型中,改变可调模型的输出推算值,使推算值与期望值之间的误差趋近于零,进而实现模型参考自适应系统的自适应控制。
3.1 基于转子磁链的转速辨识方法
计算转子磁链的电压模型:
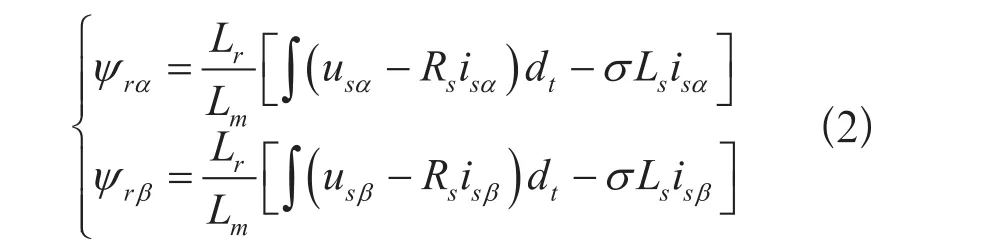
电流模型:
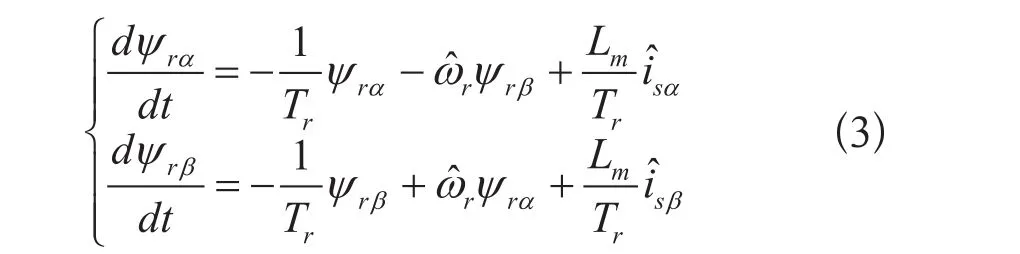
式(2)不含转速信息,可将式(2)计算得到的转子磁链作为期望值,将式(3)作为输出转子磁链估算值的可调模型。根据超稳定性理论,取自适应律为比例积分。图1为基于转子磁链的MRAS转速辨识系统框图。其转速辨识公式为:
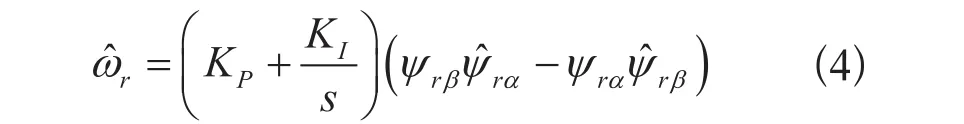
由MRAS理论可知,利用模型参考自适应法对电机进行转速辨识时,系统的转速辨识精度与参考模型的准确性息息相关。电压模型中含有积分运算和定子电阻,给系统带来积分初始值和直流偏移的问题,同时定子电阻随电机的温度和频率变化而发生改变,从而影响电机转速辨识精度。电机运行在低速状态下,定子电阻所占压降较大,造成转速估算误差较大,或可导致控制系统无法稳定运行。基于转子磁链的MRAS转速辨识系统,如图1所示。
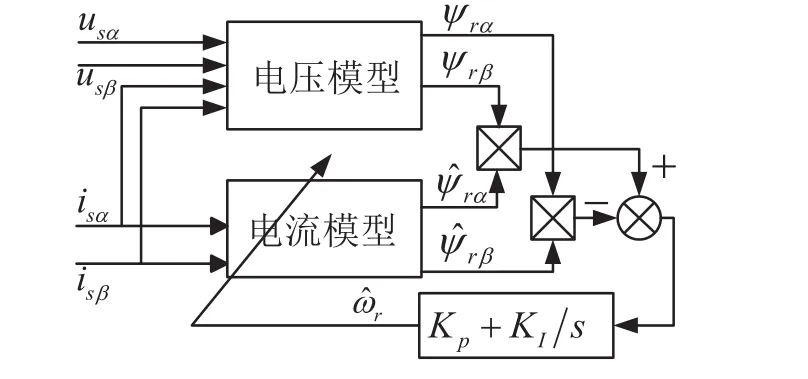
图1 基于转子磁链的MRAS转速辨识系统
3.2 基于无功功率的转速辨识方法
由异步电机在两相静止坐标系下的状态方程,推出电机的反电动势方程为:
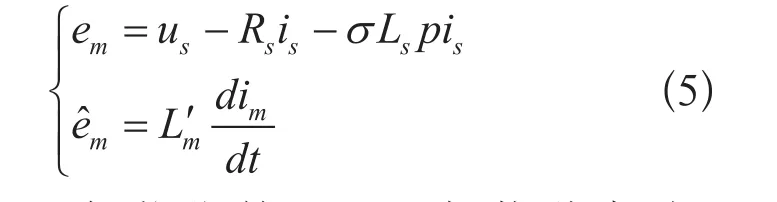
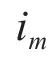
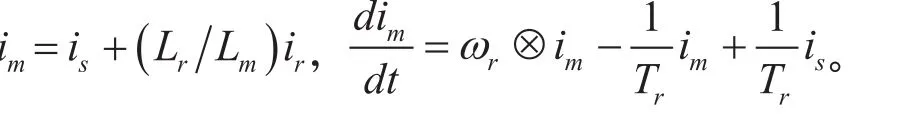
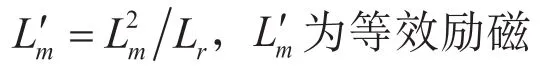
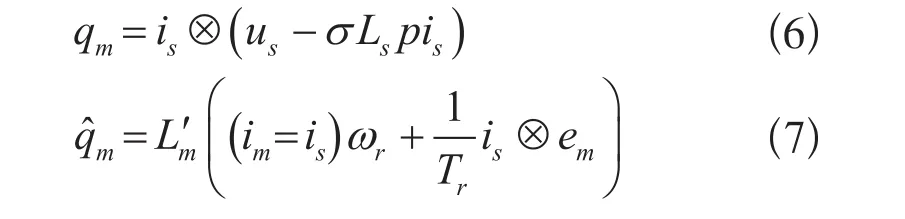
在αβ坐标系下,式(6)和式(7)可改写为:
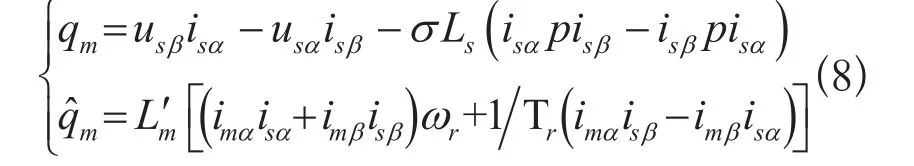
同理,自适应律选为PI控制,可得基于无功功率的MRAS系统转速辨识机构,如图2所示。
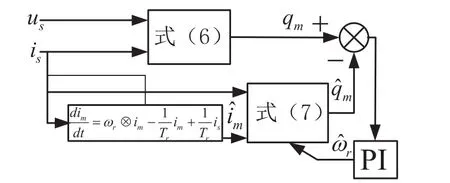
图2 基于无功功率的MRAS系统转速辨识
系统转速辨识公式为:
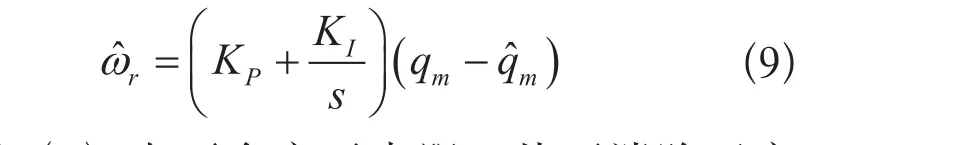
式(6)中不含定子电阻,从而消除了定子电阻对系统的影响,增强了系统对定子电阻的鲁棒性,减小了电机参数变化对系统的影响,同时去除参考模型中的积分运算,加快系统的响应和收敛速度,提高系统转速辨识精度。
3.3 基于定子电流的转速辨识方法
基于定子电流的MRAS系统的结构,如图3所示。其原理是将电机本身作为参考模型,电机定子模型和转子磁链电流模型结合在一起,共同作为系统的可调模型。用可直接测量的电机定子电流作为参考变量,与定子电流模型估算的定子电流进行差值比较,电流矢量差值信号经自适应调节机制后输出估算转速,估算转速反馈至可调模型更新估算的定子电流大小,使定子电流估算值无限逼近真实值。当系统稳定后,电机估测转速应等于电机的实测转速。
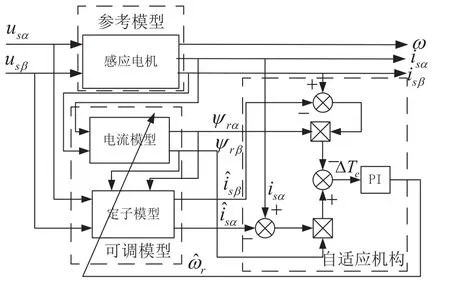
图3 基于定子电流MRAS系统转速辨识
两相静止坐标系下的感应电机定子模型:
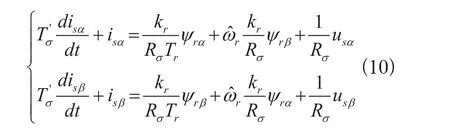
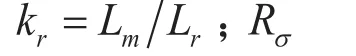
由式(10)可知,要得到估算定子电流,需得到电机的转子磁链。由于计算转子磁链的电流模型相比电压模型更适合于低速,故采用式(3)计算得到转子磁链。
自适应机构:
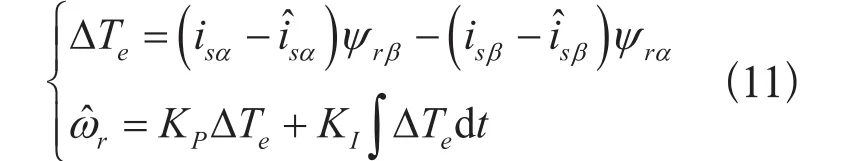
基于定子电流的MRAS系统以电机本身作为参考模型,以可直接测量的定子电流作为参考变量,消除了以电压模型作为参考模型时系积分运算和定子电阻给系统带来的影响。故该方法可获得较好的低速性能且拓展了系统的调速范围。
4 辨识转速对定子电阻敏感性分析
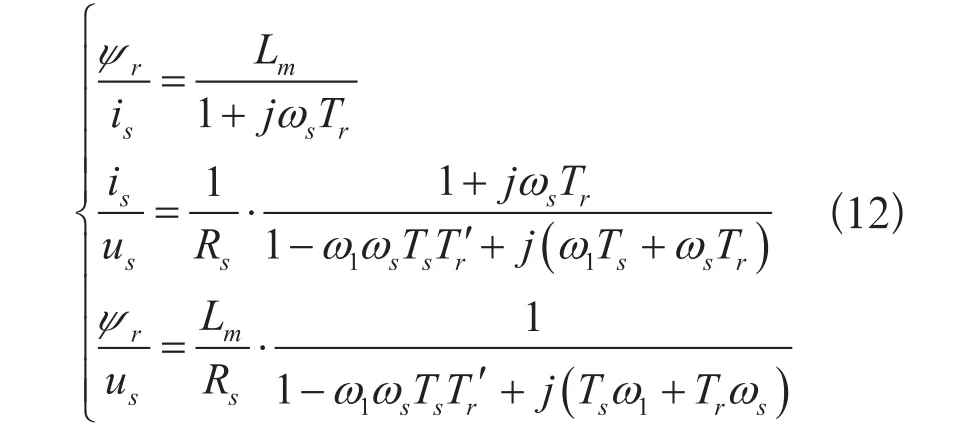
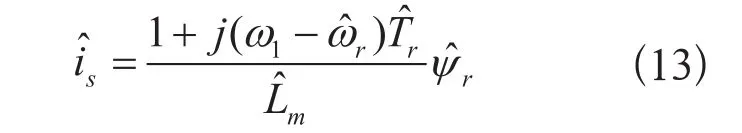
估算转子磁链与定子电压的关系为:
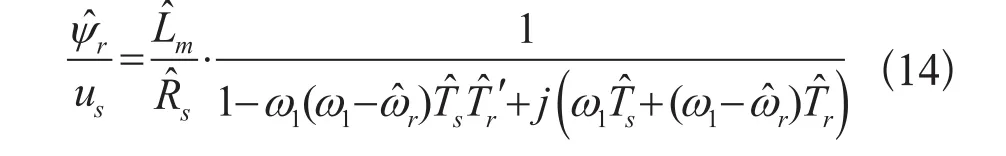
联立式(12)第二行与式(14),得到实际定子电流与估算磁链的关系为:
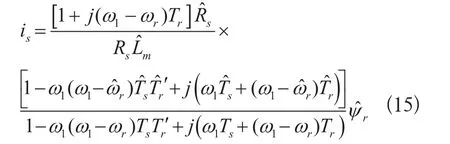
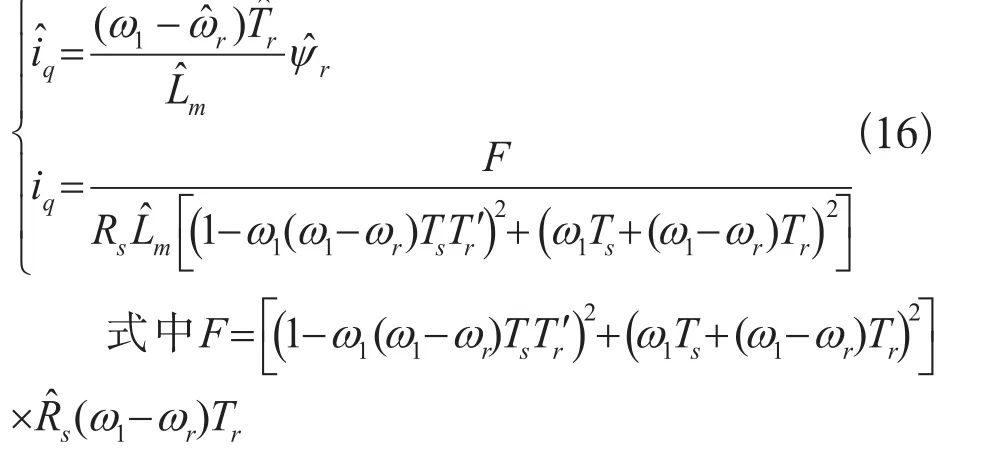
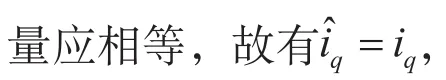
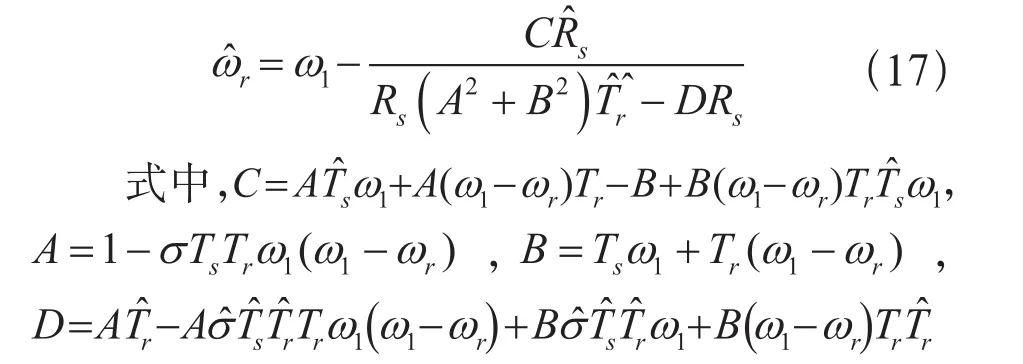
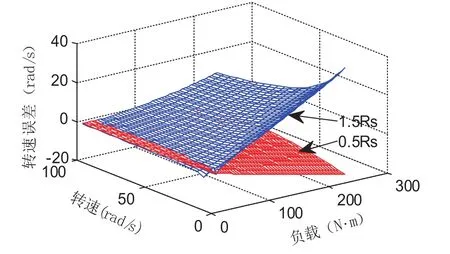
图4 辨识转速对定子电阻的敏感性三维图
由图4可知,电机运行的转速越低,负载转矩越大,系统的转速误差越大,即定子电阻对转速的辨识精度的影响越大,将影响整个系统的控制性能。
5 仿真研究
模型参考自适应系统如图5所示。
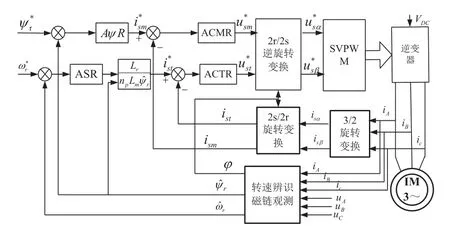
图5 基于MRAS的无速度传感器矢量控制系统
在MATLAB仿真平台上搭建基于三种转速辨识方法的异步电机MRAS系统。电机参数如下:额定功率:15 kW,额定电压:380 V,额定频率:50 Hz,定子电阻:Rs=0.4 Ω,定子自感:Ls=0.087 H,转子电阻:Rr=0.5 Ω,转子自感:Lr=0.088 H,互感:Lm=0.085 H,极对数:P=2,转动惯量:J=0.87 kg.m2,阻尼系数:0.001 kg.m2/s,转子时间常数:Tr=0.176,电机漏磁系数:σ=0.0 563。
图6~图8为电机在低速状态下的转速响应。给定转速为50 r/min。电机空载启动,t=1 s时突加50 N·m负载,在t=2 s时实现负载突变,负载为-50 N·m。t=3 s时电机转速由50 r/min改为-50 r/min,实现电机的正反转。由图可知,三种转速辨识方法的控制系统均可在低速状态下运行,具有较好的稳定性。基于转子磁链的模型参考自适应系统转速超调量较大,为40 %,且当电机实现反转后,转速稳态误差为5 r/min。基于定子电流的MRAS系统转速超调量最小且动态响应最好。
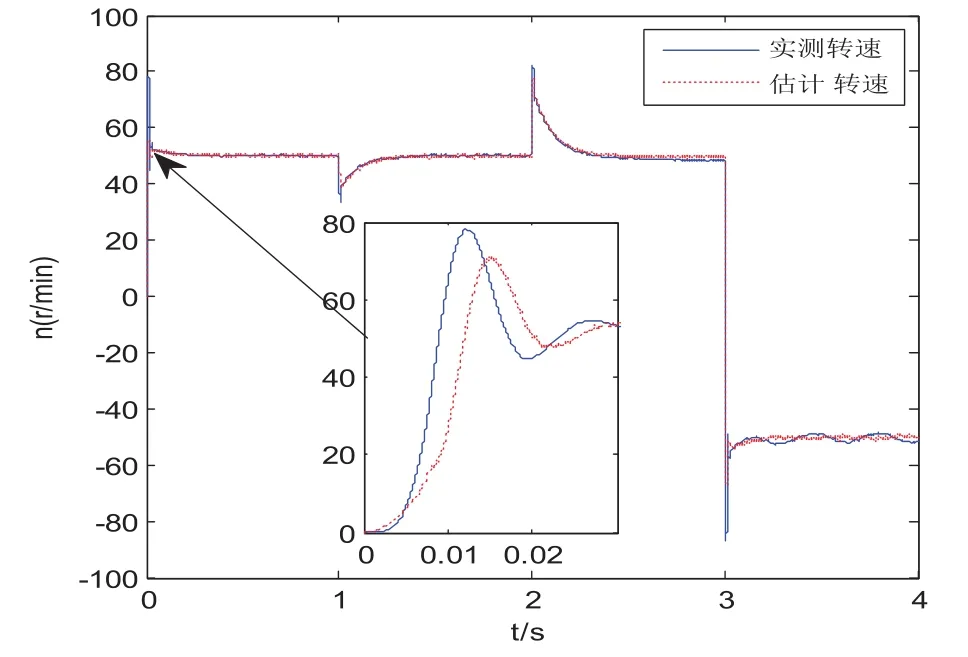
图6 基于转子磁链MRAS系统转速响应
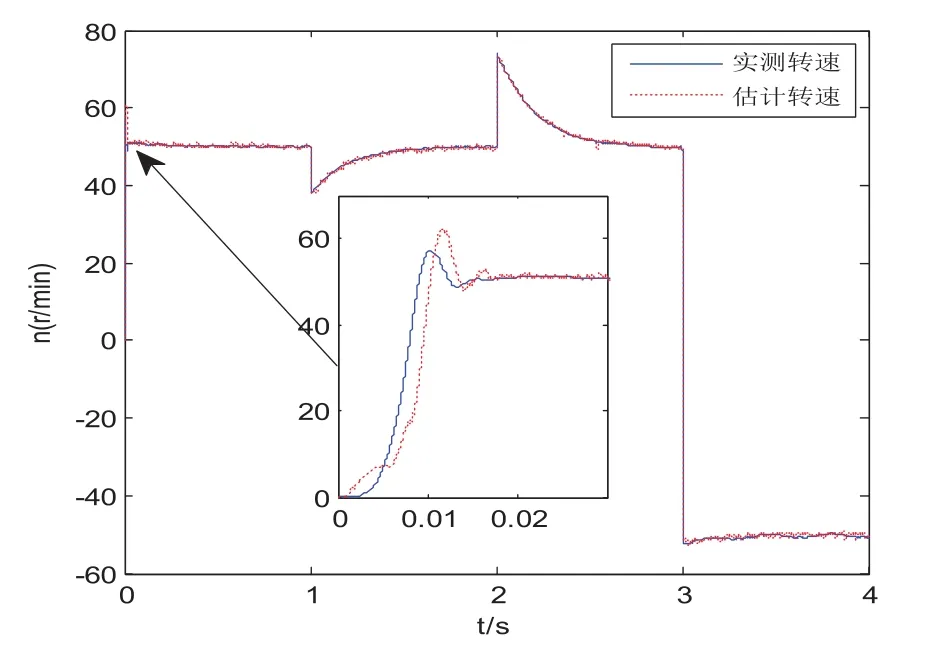
图7 基于无功功率MRAS系统转速响应
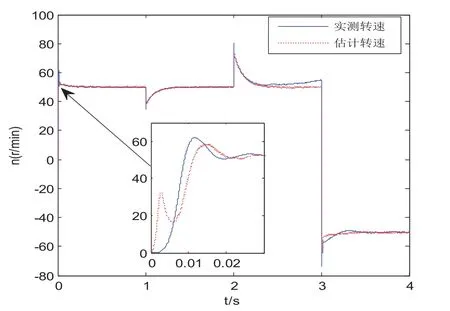
图8 基于定子电流MRAS系统转速响应
在实际工程中,电机的定子电阻因电机温度变化等原因而发生改变。假设定子电阻增加至1.2 Rs,其他参数不变。图9~图11为定子电阻为1.2 Rs时三种MRAS系统在低速状态下的转速响应图。仿真时间为3 s,电机在给定转速为50 r/min时空载启动,在t=1.5 s时突加10 N·m的负载。基于转子磁链的MRAS系统,无论空载还是带载情况下其转速波动都较大,在实际的运行工况中该系统已不能正常工作。且估测转速不能较好跟随实际转速,系统的跟随性能较差。由图10可知基于无功功率MRAS系统的超调量为30 %,超调量较大。在t=0.5 s时实测转速达到稳定,在t=1.5 s突加10 N·m后,估算转速能够跟踪实际转速且能快速恢复稳定,转速稳态误差为2 r/min。由图11可知,基于定子电流MRAS系统的超调量为6%,在t=0.1 s时电机转速达到稳定,转速误差为1 r/min。
因此,由对比分析可知,基于定子电流的MRAS系统对定子电阻变化具有良好的鲁棒性;其次为基于无功功率的MRAS系统;而传统的MRAS系统对定子电阻变化的鲁棒性较差。
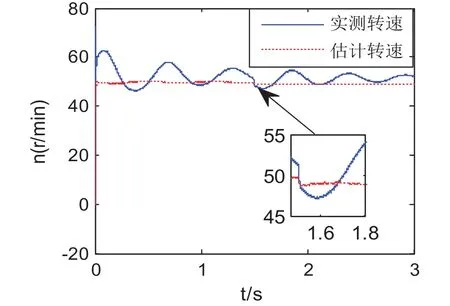
图9 基于转子磁链MRAS系统转速响应(1.2 Rs时)
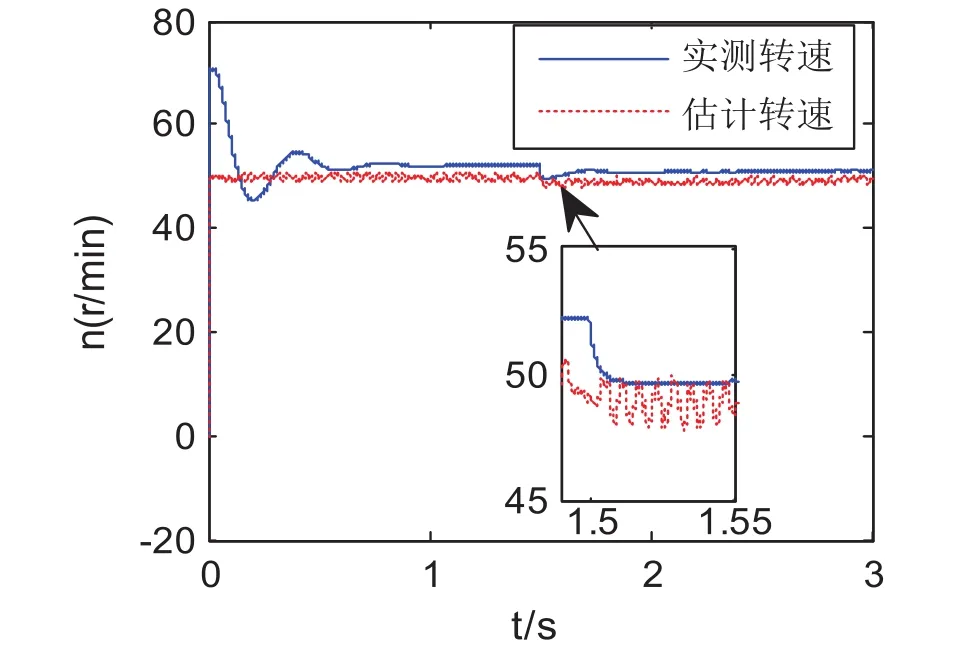
图10 基于无功功率MRAS系统转速响应(1.2 Rs时)
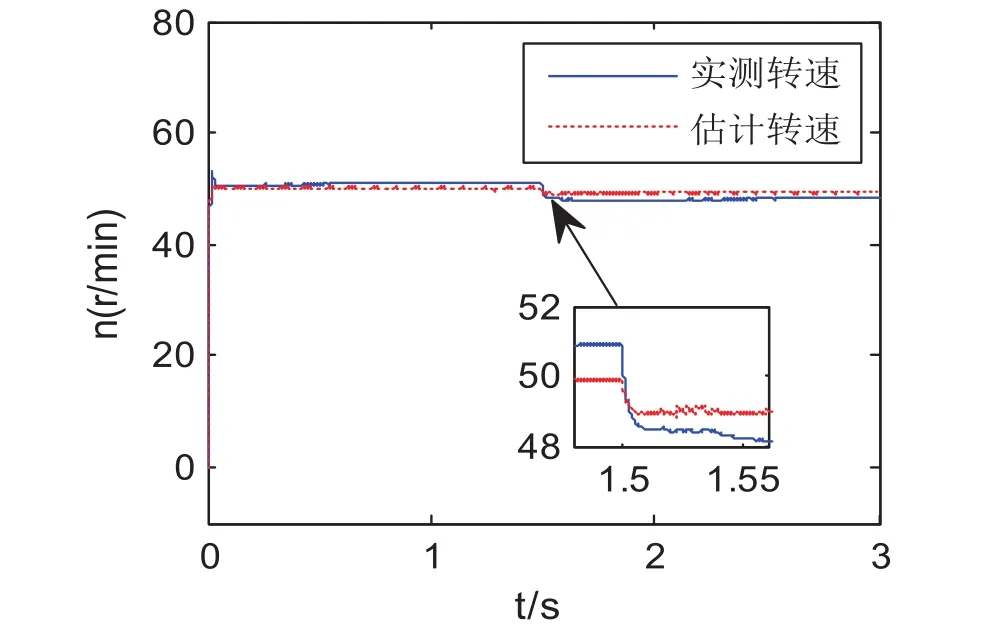
图11 基于定子电流MRAS系统转速响应(1.2 Rs时)
6 结语
结合感应电机的数学方程,推导基于三种转速辨识方法的MRAS系统各自的参考模型及可调模型,从理论上分析参考模型中定子电阻存在的影响以及辨识转速对定子电阻的敏感性。仿真结果表明:电机工作在低速状态下时,三种MRAS系统表现出对定子电阻不同的鲁棒性。基于定子电流的MRAS系统对定子电阻变化表现出良好的鲁棒性,基于无功功率的MRAS系统次之,而传统的MRAS系统对定子电阻的鲁棒性最差。
[1]周有为,刘和平,刘述喜.感应电动机无速度传感器矢量控制综述[J].微电机,2006,39(4).57-60.
[2]Kumar R, Das S, Syam P Review on model reference adaptive system for sensorless vector control of induction motor drives [J]. Electric Power Applications, IET, 2015,9(7): 496-511.
[3]电力拖动自动控制系统:运动控制系统[M].北京:机械工业出版社,2003.
[4]王 高 林,陈 伟,杨 荣 峰,等.无 速 度 传 感 器 感 应电机改进转子磁链观测器[J].电机与控制学报,2009,13(5):638-642.
[5]Haron A R, Idris N R N. Simulation of MRAS-based speed sensorless estimation of indu-ction mot-or drives using MATLAB/SIMULINK[C]. 2006 IEEE International Power and Energy Conference. IEEE, 2006,10(4):411-415.
[6]刘 丽 娟,童 军,乔 江,等.一 种 在 线 辨 识 定 子 电阻的MRAS转速估算方法[J].电机与控制应用,2015,42(10):1-5.
[7]廖晓钟.感应电机多变量控制[M].北京:科学出版社,2014.
[8]Wu Z, Zhi D, Ying J. Research on speed estimation algorithm for induction motor drive[C]. Power Electronics and Motion Control Conference, 2004. IPEMC 2004. The 4th International. IEEE, 2004, 5(3): 1387-1392.
[9]王丙元,冯辉.基于定子电流的模型参考自适应感应电机转速估算[J].电机与控制学报,2013,17(9):48-56.
[10]邓歆.异步电机全阶磁链观测器的设计分析及其应用研究[D].武汉:华中科技大学,2010:75-79.
