基于滑模观测器的PMSM模型预测控制

李超，朱军，孙顺新

（ 1.山东医学高等专科学校附属医院，山东 临沂 276000;2.临沂市恒源热电集团有限公司，山东 临沂 276000;3.天元建设集团有限公司，山东 临沂 276000 ）

0 引言

随着全球经济的快速发展，电动车成为了新能源背景下的重要产物。其驱动核心——永磁同步电机（Permanent magnet synchronous motor）的控制成为研究的关键。永磁同步电机具有体积小，结构简单，效率高，输出转矩大，过载能力强等优点，传统PMSM控制方法为PI控制，其参数调整依赖于操作者的经验，在电汽车的驱动中已经不能满足交流伺服系统的高性能要求。

预测函数控制（Predictive Functional Control，PFC）作为一种模型预测控制方法，具有控制量计算方程简单，实时控制计算量小，跟踪精度高等特性，已经广泛应用于现代生产过程控制中。近年来，国内研究学者对该模型预测控制进行了大量的研究。本文针对PMSM控制系统的控制精度及动态响应要求的问题，提出了带扰动补偿的PMSM模型预测控制策略。利用模型预测控制方法，设计预测速度控制器，提高了电流环跟踪精度和电机启动性能。为提高系统的抗扰性能，设计离散滑模扰动观测器，有效地估计外部扰动并对系统进行前馈补偿，提高了系统的鲁棒性。仿真及实验结果验证了该方法的有效性。

1 数学模型

以PMSM为控制对象，假定永磁体无阻尼作用且空间磁场呈正弦分布，忽略磁滞和涡流损耗的条件下，P采用id=0的矢量控制方式的数学模型为

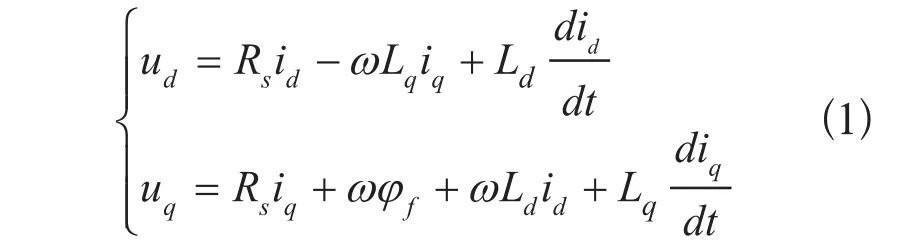
PMSM转矩方程为：

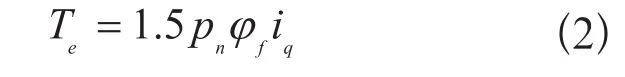
PMSM运动方程为：

式中：ud，uq分别为d，q轴电压；id，iq分别为d，q轴电流；Ld，Lq分别为d，q轴电感；且Ld=Lq；Rs为定子电阻；Te为电磁转矩，pn为电机的极对数；φf为永磁体与定子交链的磁链；TL为负载转矩；J为转动惯量；ω，ωr分别为转子的电角速度和机械角速度；B为粘滞系数。

2 离散扰动观测器设计

为提高动态精度与电机控制系统的抗扰动能力，将离散扰动观测器实时估计的扰动观测值引入速度环的控制中。

永磁同步电机参数发生变化时运动方程（3）式可描述为：

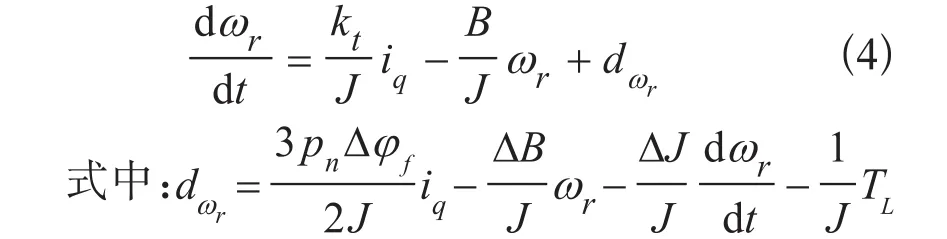
令x=ωr作为状态变量，u=iq为输入变量，d= 为扰动变量，Y=ωr为输出变量，则对式（4）进行离散化可得：

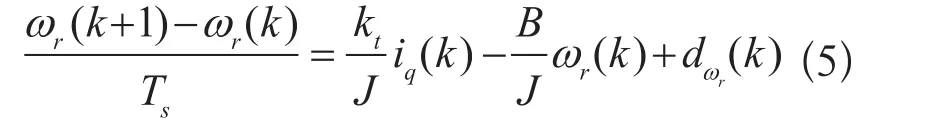
则式（5）可以整理成如下式：

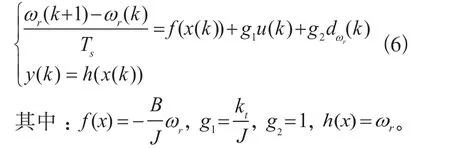
构建非线性干扰估计式：

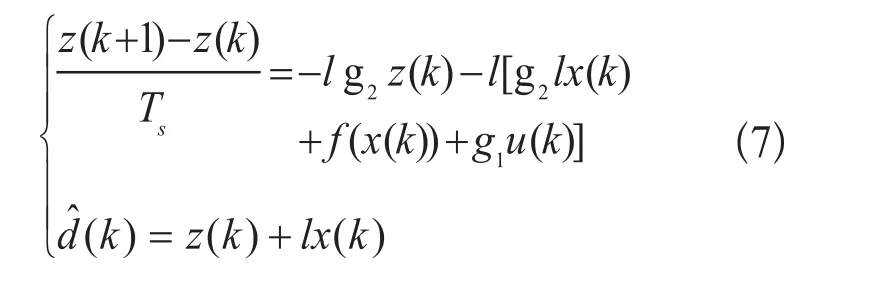
其中： 和z分别为扰动变量 的估计变量和非线性干扰观测器的内部状态变量，l为扰动观测器的增益矩阵。

3 速度预测函数控制器设计

3.1 预测函数控制模型

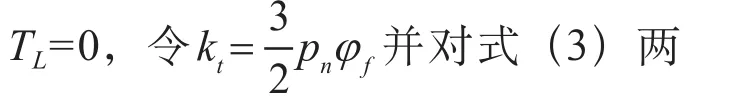
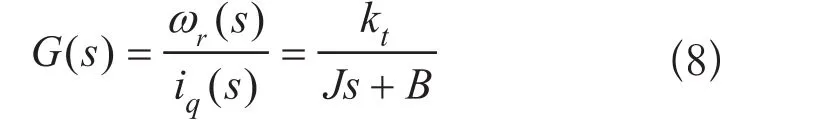
预测函数是一类基于模型的计算机算法，但是计算机只能处理离散的信号，因此需要对永磁同步电机模型进行离散化处理，利用零阶保持器对其进行离散处理，后对（8）式求Z传递函数，可得：

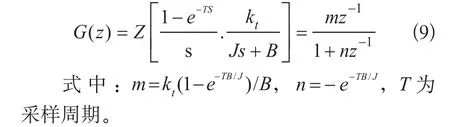
对式（9）求差分方程得：

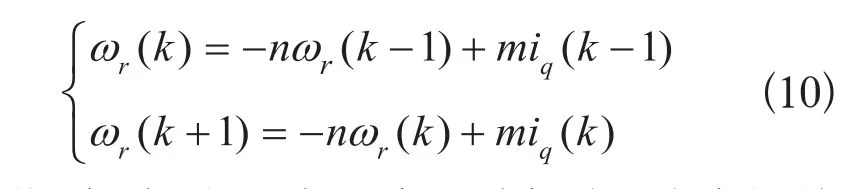
将（10）中两式相减得到永磁同步电机转速的预测模型为：

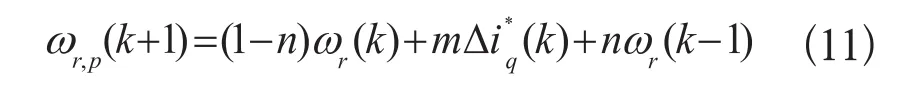
式中：ωr,p(k+1)为(k+1)T时刻预测模型的预测转速，ωr(k+1)是kT时刻ωr(k+1)的实际转速，Δi*q(k)为kT时刻q轴的电流增量。

3.2 滚动优化

通常情况下，考虑到对象的动态特性，一般希望系统输出沿着期望的轨迹，平滑过渡到参考值。按照稳定性的要求，参考轨迹采用一阶指数形式，表达式为：

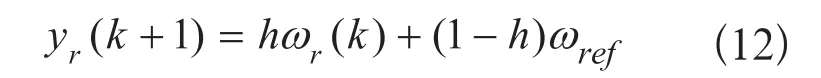
式中：ωref为设定值，h=e-T/τ，τ为参考轨迹时间常数。

3.3 反馈校正

由于系统存在着外部扰动和模型失配的影响，因此需要对转速进行反馈校正，采用转速误差直接对预测输出进行补偿，补偿量为实际转速和预测转速的误差e(k)=ωr(k)-ωr,p(k)，在(k+1)T时刻经过校正后系统的预测输出转速为：

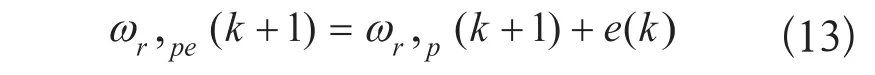
在此基础上需要确定最优控制律，通常选用二次型性能指标，二次性能指标采用输出预测误差和控制量的加权，不仅可使预测输出最大程度的接近期望输出，同时又可避免控制增量剧烈变化，二次性能指标函数为：

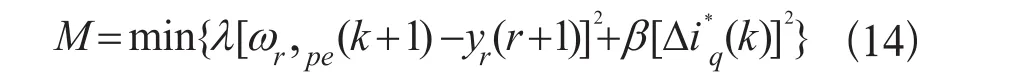
式中：λ和β分别为预测误差输出和控制量变化的加权系数，分别表示对跟踪误差及控制量变化的抑制作用。

由此得到优化控制函数如下：

求解优化控制函数M对于Δiq*(k)的导数，并根据极值求解条件求得控制量的增量：

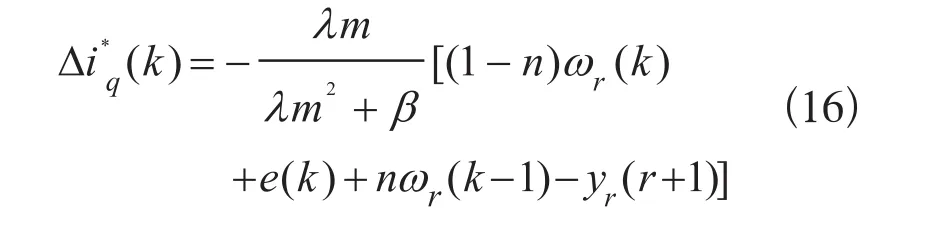
则在kT时刻实际的控制量为：

4 仿真实验

PMSM调速系统原理如图1所示。采用MATLAB/Simulink搭建了系统仿真模型，选用PMSM的参数见表1。

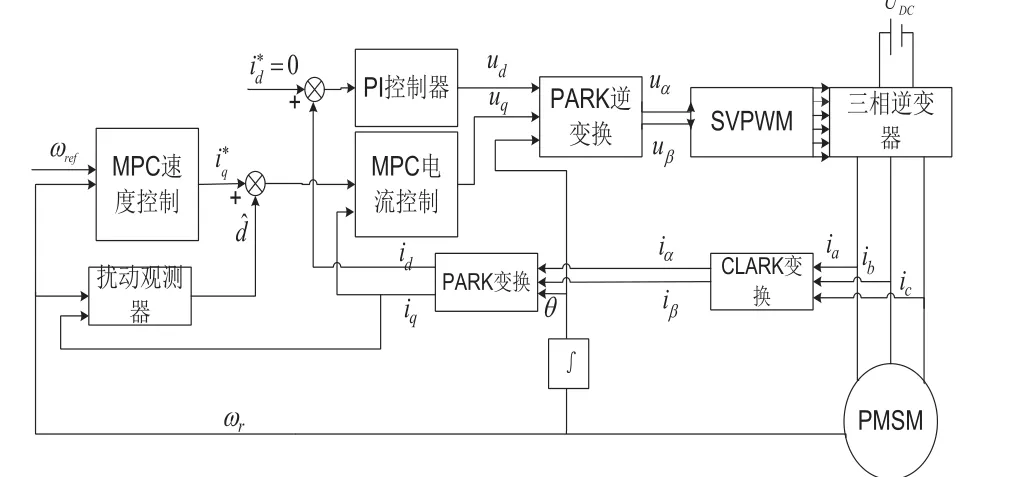
图1 PMSM控制系统结构

表1 永磁同步电机参数

为更好的验证本文设计控制系统的转速响应以及抗扰动性能，将其与传统PI控制器，以及不带扰动补偿的双预测函数控制器进行比较，仿真的结果验证了方法的有效性。

图2为本文控制方法未加载时对应的速度响应曲线，图中可见在未加载时始能迅速达到给定值且速度平稳。

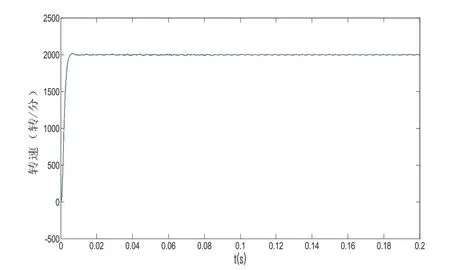
图2 转速响应仿真曲线

图3 为电流响应曲线，可见电流响应速度快，正弦度较好。图4为系统转速曲线，从图中分析可以得出，该方法具有较好的抗扰性能。

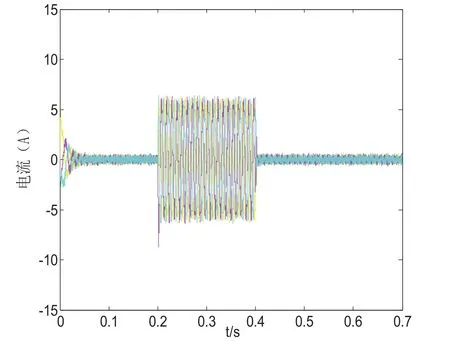
图3 加载和减载时定子电流仿真曲线

图4 加载和减载时的转速仿真曲线

图5 所示扰动观测值曲线，达到了较为理想的效果。从仿真结果可见，该调速系统的转速控制方法，具有转速无超调，响应速度快，抗扰动性能强等一系列优点。

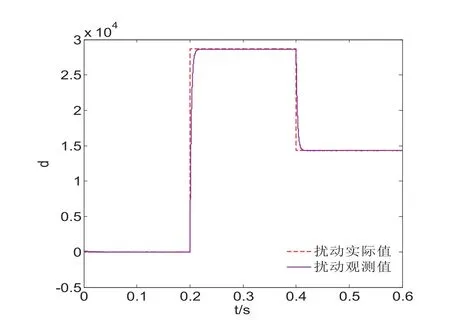
图5 扰动实际值与扰动估计值仿真曲线

5 结语

本文利用模型预测控制理论设计了PMSM双环预测控制器，提高了系统的电流跟踪精度和转速控制精度。针对系统的鲁棒性问题，设计了滑模观测器，估计系统扰动对控制量进行补偿，提高了系统的鲁棒性。仿真结果表明该方法显著提高了系统的动态性能和静态性能，达到预期效果。

[1]毛永乐，杨家强，赵寿华.带负载转矩估算的非线性观测器内嵌式永磁同步电机无位置传感器控制策略[J].中国电机工程学报，2016，36(8)：2252-2254.

[2]陆婋泉，林鹤云，韩俊林.永磁同步电机的扰动观测器无位置传感器控制[J].中国电机工程学报，2016，36(5)：1387-1388.

[3]Matteo Carpaneto, Paolo Fazio, Mario Marchesoni.Dynamic Performance Evaluation of Sensorless Permanent-Magnet Synchronous Motor Drives With Reduced Current Sensors[J]. IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, 2012,59(12):4579-4582.

[4]符慧，左月飞，刘闯.永磁同步电机转速环的一种变结构PI控制器[J].电工技术学报，2015，30(12)：237-238.

[5]王东文，李崇坚，吴尧.永磁同步电机的模型预测电流控制器研究[J].电工技术学报，2014，29(1)：73-75.

[6]牛里，杨明，刘可述.永磁同步电机电流预测控制算法[J].中国电机工程学报，2012，32(6)：131-137.

[7]杨洪金，井元伟，肇和平.非线性系统观测器的设计：LMI方法[J].信息与控制，2011，40(4)：433-435.

[8]Yang J, Member.do. Sliding-Mode Control for Systems With Mismatched Uncertainties Via a Disturbance Observer[J].IEEE Transactions on Industrial Electronics 2013, 60(1):4398-4407.

[9]Chen W H, Member. A Nonliner Disturbance Observer for Robotic Manipulators[J]. IEEE, 2000, 47: 1943-1947.

[10]邓永停，李洪文，王建立.基于预测函数控制和扰动观测器的永磁同步电机速度控制[J].光学精密工程，2014，22(6)：1598-1605.

[11]刘旭东，李珂，孙静，等.基于广义预测控制和扩展状态观测器的永磁同步电机控制[J].控制理论与应用，2015，22(12)：1055-1065.

[12]YANG J,LIU H X,LI S H. Nonlinear Disturbance Observer Based Robust Tracking Control for a PMSM Drive Subject to Mismatched Uncertainties[C].//31th Chinese Control Conference H F, China: IEEE Transactions on Industrial Electronics,2012: 222-227.

[13]侯利民，张化光，刘秀翀.带ESO的自适应滑膜调节的SPMSM自抗扰-无源控制[J].控制与决策，2010，25(11)：1651-1654.