多轴联动木工雕刻机加工速度衔接的研究与仿真1)

2018-03-07王发利边继龙张俸铭葛林马辉陈广俊

东北林业大学学报 2018年2期

王发利边继龙张俸铭葛林马辉陈广俊

(东北林业大学，哈尔滨，150040) (哈尔滨雅智科技有限公司)

随着精雕市场需求的日益增长、科技的发展和制造技术的进步，传统的手工雕刻已经被自动化雕刻系统取代，木工雕刻机已成为木工雕刻行业的首选工具。而传统的三轴数控系统雕刻机，工件加工需多次装夹完成，存在精度差、效率低、速度慢等缺点。多轴数控加工中心集先进的结构设计技术、计算机控制、高性能伺服驱动和精密加工技术于一身，广泛应用于木工雕刻、金属切削、模具等行业，制造水平显著提高[1]。笔者阐述的新型多轴联动木工数控雕刻机主要用于工艺扇窗等材料的加工，能够高质量地完成雕刻、切割、镂空、打孔等工艺要求。木工数控雕刻机运动控制系统的核心功能是根据数控指令，驱动伺服系统按指定规律运动。在数控加工领域，数控系统多工作在位置控制模式。此时数控指令由大量小段直线和圆弧确定，运动控制系统依照指令中给定的坐标，驱动刀具沿指定轨迹运动，近似拟合出形貌。根据微积分原理，任意连续可微曲线可通过线段逼近，所以研究线段的执行运动是控制系统的核心问题。

在处理多段直线轨迹过程中，由于运动速度无法突变，就需要考虑当前段与前后段的衔接，这项工作被称为速度衔接，也称作前瞻速度规划或速度控制等。衔接的目标是在前后相邻两段末速度与初速度差异不超过机构设计指标的情况下，尽可能提高运动速度。很显然，速度衔接算法的优劣对加工质量与效率有着很大影响。

对速度衔接问题，国内学者进行了不少研究。早期曹荃[2]等将无拐点的相邻路径段作为整体合并处理，但无法推广到一般情况。叶佩青[3]、王宇晗[4]等人在国内较早提出了小段衔接的数学模型，前者在建立拐角模型的时候采用了圆弧近似的方法，后者用几何法给出了小线段过渡时初末速度的约束条件，建立了衔进给速度的递归不等式模型。任锟[5-6]等采用三次样条曲线拟合离散加工路径，发现高曲率点，根据加减速特性预估拐点处的最优速度。此后的不少研究[7-16]都是对前述几种方法的实现与细节优化。这些算法的共同特点：①适应性低。这些算法均将加工设备各轴的加速度视为统一定值，不随时间变化。而在多轴联动数控系统中，各轴允许的加速度可能有很大差别，现有算法并未深入探讨这一问题。此外，由于伺服电机具有一定的瞬时加速能力，在段间衔接时，可以采用较高的加速度以提高运动效率并减少速度波动。这种能力在快速成型[13]等高速、轻载且对运动速度平稳性要求较高的应用中有着重要意义。②计算量大。现有算法都以前后两条线段夹角作为加减速衔接参数，这就需要三角函数和较多的开方运算。文献[3]、[6]、[17]采用二阶或高阶曲线拟合刀轨时需要解非线性方程或方程组，致使低端嵌入式处理器难以实现实时多轴控制，极大地限制了算法的应用范围。

本研究基于矢量分析和最优化方法，提出了一种速度衔接算法，可高效灵活地实现任意多轴速度衔接。与现有算法相比，具有以下特色与优势：①在理论上，作为文献[4]算法的推广，支持任意多个加速度上限不同的运动轴，并支持段内和衔接时设置不同的加速度，使得算法具备了极大的灵活性。②在求解方法上，本研究算法直观性强，计算简单，仅需要四则运算和一次开方运算即可完成，不需要三角函数运算，五轴控制也可以在低端嵌入式处理器中实时完成。

1 任意多轴联动速度衔接算法

1.1 速度衔接的基本原理

速度衔接问题本质上是一个最优化问题，是在当前段和前后若干段速度、加速度、位移等条件的约束下，求解每一段的初速度(入口速度)和末速度(出口速度)，令各段运动速度最高。对于步进和伺服电机而言，都有一定瞬间改变运动速度的能力(下文称为瞬时换向，简称换向)，这种能力最常体现在电机启动时，在负载合适的情况下，电机可以以一定转速(对步进电机而言是步进频率)直接瞬时启动，例如本研究中步进电机允许启动速度约为1rad/s。同样，电机在运动过程中也可以瞬时改变速度，此时瞬时加速度是正常加(减)速过程中加速度的几十倍至上百倍。对负载轻，且对速度稳定和效率要求较高的应用，应当充分利用瞬时换向能力，使相邻两段都能以较高速度运动。根据上述分析，速度衔接时的约束条件主要包括：①初速度、末速度大于0且小于等于数控指令规定的该段运动速度(简称标称速度)；②以初速度开始，通过加(减)速，在该段位移内能加(减)速到末速度；③前一段末速度矢量与当前段初速度矢量各分量差的绝对值不超过对应轴的换向速度上限。

从上述约束条件可以看出，初速度主要受到上段和本段标称速度，本段末速度和加速度的约束，而本段末速度又受下段速度的约束。很显然在初次进行一段速度衔接时，只能暂不考虑下段，仅根据本段情况做出最保守的衔接，是不可能做到最优的，所以速度衔接必然是一个迭代过程。

1.2 初次速度衔接处理

初次速度衔接处理是指在没有后段信息的情况下，求解上段出口速度和当前段入口速度。初次速度衔接处理的已知条件是：①本段和上段基准轴标称速度，速度以步进频率表示，基准轴是指频率最高的轴。在多轴联动的情况下，求出基准轴初、末速度，自然可以按比例求出其他轴速度；②系统加速度，即单位时间步进频率的变化率；③本段和上段位移，以步为单位；④各轴换向速度上限。

根据上述条件还可以推出本段初速度上限和上段末速度上限，都是针对各自基准轴而言的。初速度上限Vmax由基准轴最大换向速度(V0)、加速度(a)、位移(s)和标称速度(V)决定：

(1)

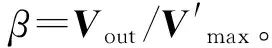
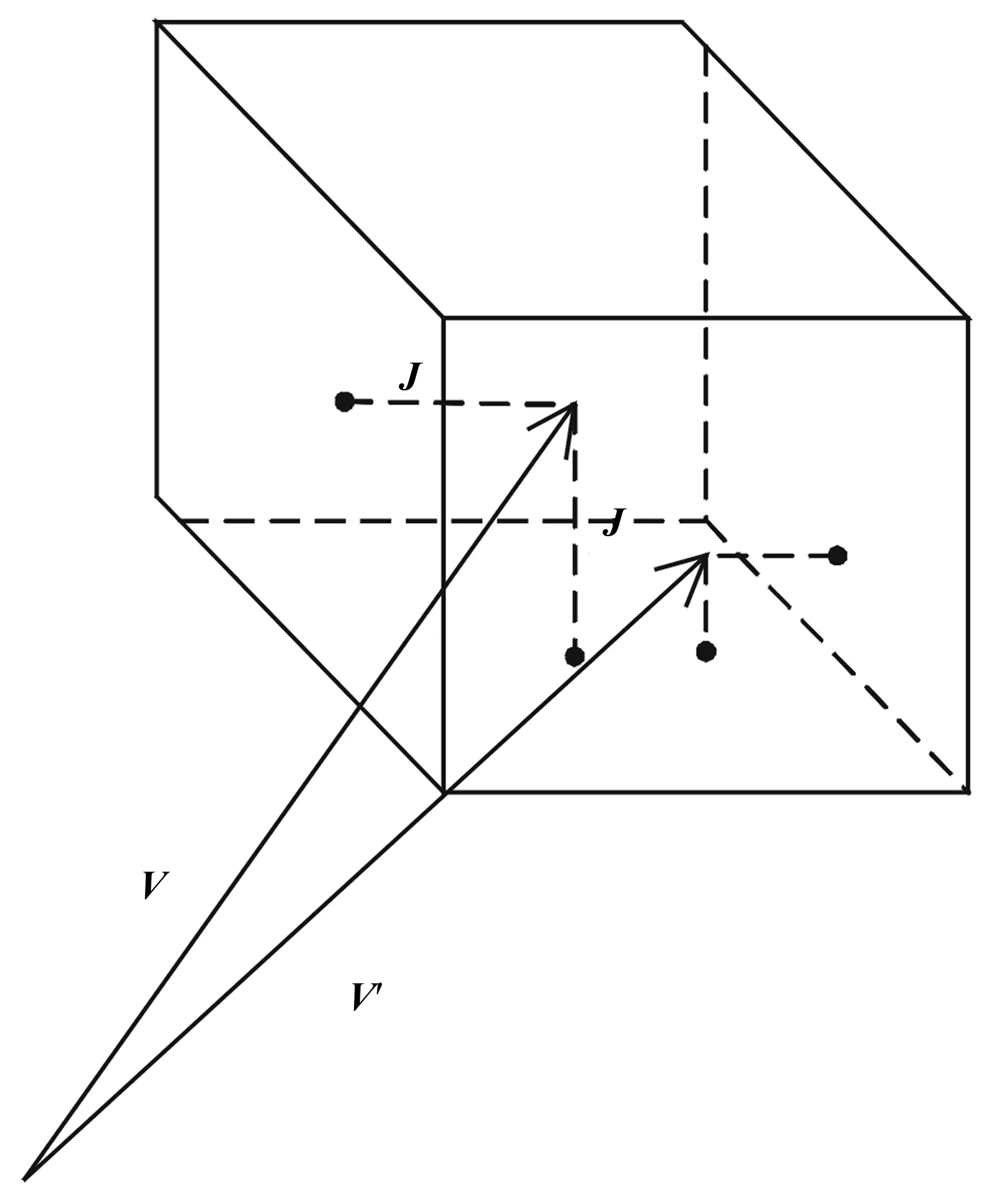
图1 两段均无需减速

1.2.1 同向衔接处理

同向衔接是指前后两段速度矢量各分量方向均相同(含速度分量为0的情况)时，进行衔接计算的过程。此时对速度衔接的约束条件为：

(2)

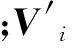
同向衔接的任务就是在约束条件下，求出最大的α和β。从几何角度看，对于n轴联动的系统来说，相当于以2Ji为边长，在n维空间构造一个长方体，若将其中心置于向量V顶点处时，与向量V′没有接触，则将其中心沿向量V滑动，直至与向量V′接触。通过几何关系可以看出，2个向量间的关系有3种情况。第1种情况如图1所示，两个速度向量距离较小，都不需要减速即可完成衔接；第2种情况如图2所示，前后两段中V′需要减速，V不需要减速；第3种情况如图3所示，是两段都需要减速。第1种情况要求各轴速度分量差的绝对值都小于最大换向速度，初速度就是初速度上限，末速度就是上段末速度上限。第2种情况，其中一个向量穿过了长方体。此时应当存在一个轴i，使得两个向量满足式(3)的条件：

(3)

式中:i≠j。实现时可按公式(3)的条件对所有i进行穷举，如不存在这样的轴，则将V与V′互换，再穷举一次。第3种情况下应存在两个轴，使得两个向量满足公式(4)的条件：

(4)

在实现时，可对i、j进行穷举，对满足条件的α和β还应进行校验，条件如公式(5)所示：

(5)

式中:k≠i,j。这个条件表示向量与长方体的边直接接触，而不是和长方体边的延长线接触。

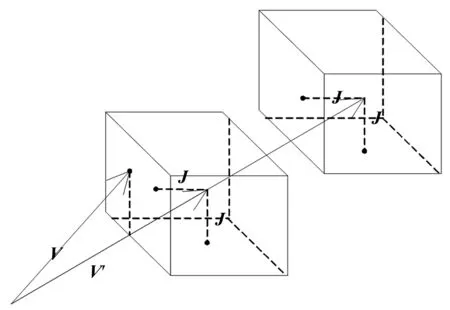
图2 一段减速，另一段不减速

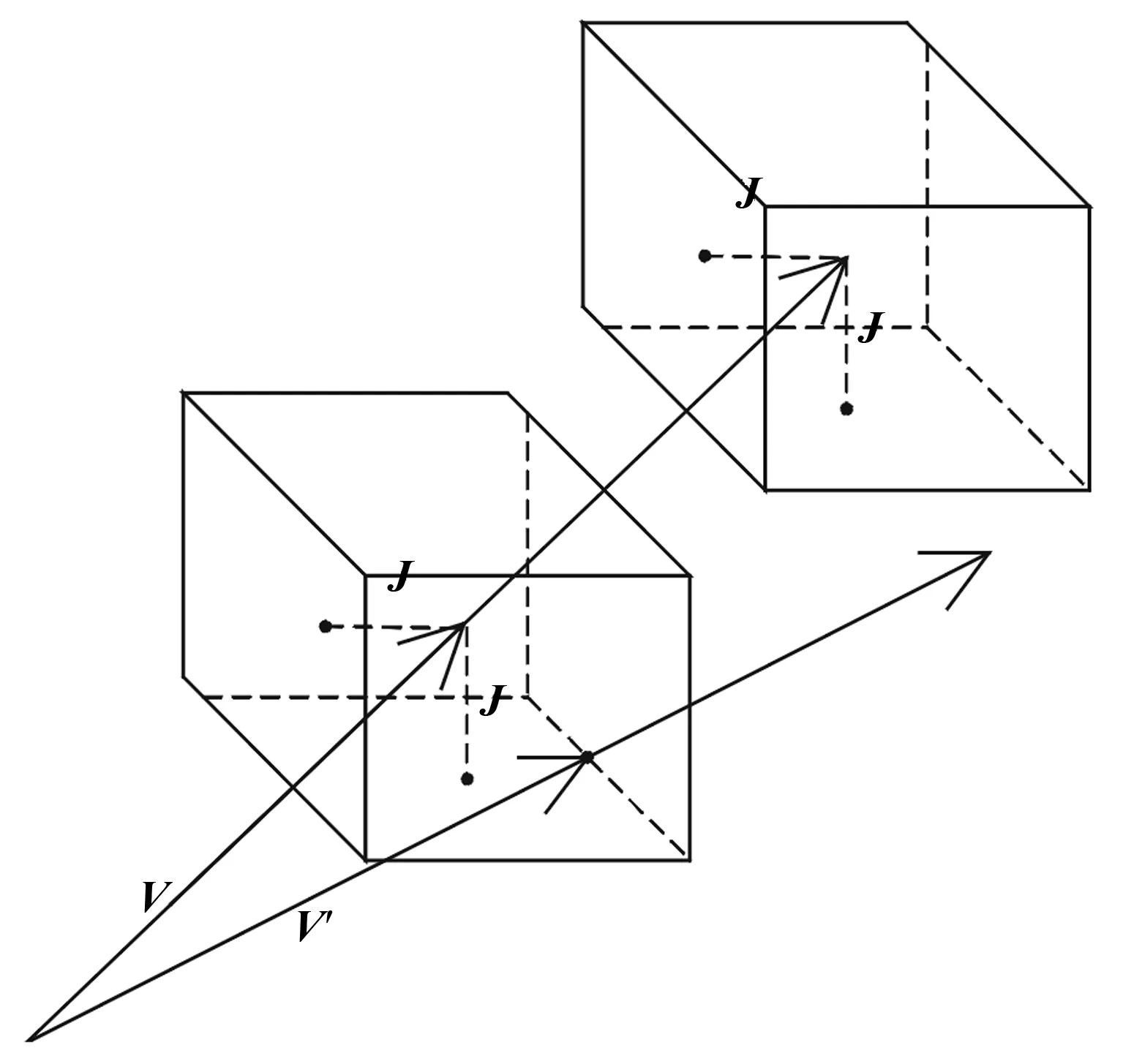
图3 两段均需减速

1.2.2 反向衔接处理

(6)

式中：i表示枚举所有运动方向相同的分量；j表示枚举所有运动方向相反的分量。若以α为横轴，β为纵轴，可以看出，对于同向运动的分量而言，约束条件对应两条斜率为正的平行线所夹区域，而对于反向运动的分量而言，约束条件对应一条斜率为负的直线的左侧区域。综上，目标函数的定义域是公式(6)定义的区域和正方形区域α、β∈(0,1]的交集。显然这一区域非空，因为当α、β都取足够接近于0的值时，必然能够满足约束条件。

根据上述分析，反向衔接处理问题实质上是一个有限区域内二元函数f(α,β)=αβ的极大值问题。根据初等微积分原理，极值或出现在驻点上，或出现在区域边界上。通过求偏导数可知，函数f(α,β)在整个二维平面上只有一个驻点(0,0)，这个驻点显然不是函数极大值，不符合要求。所以函数的极大值必然存在于区域边界，这样反向衔接处理问题转换为根据约束条件求定义域边界线段，以及求各线段上目标函数最大值的问题。第一步是反向衔接处理算法的核心，为保存区域各顶点，需要定义一个双向链表，各顶点在链表中按顺时针顺序存储。求解边界线段具体步骤如下：

①初始化。链表初始节点为A、B、C和D，它们的坐标分别为(0,0)、(0,1)、(1,1)、(1,0)。②如图4所示，遍历各个速度分量，对同向运动的分量逐个进行处理，即求两条平行线与原有区域的交点。③处理截距为正的直线，即图4中的L1，由点A开始，沿顺时针方向遍历所有边，求L1与各边的交点E和F；④将第一条与L1相交的边的起点A和第二条与L1相交的边的终点C间的所有链表节点(图4中的B)，删除。⑤将L1的两个交点E和F插入链表中。⑥处理截距为负的直线L2，由点A开始，沿逆时针方向遍历所有边，求L2与各边的交点。⑦将第一条与L2相交的边的起点A和第二条与L1相交的边的终点F间的所有链表节点(图4中的D)，删除。⑧将L2的两个交点(图中G和H)插入链表中。⑨如图5所示，遍历各个速度分量，对反向运动的分量逐个进行处理。⑩由点A开始，沿顺时针方向遍历所有边，求L3与各边的交点。将第一条与L3相交的边的起点B和第二条与L3相交的边的终点E间的所有链表节点(图4中的C，D)删除。将L3的两个交点(图5中F，G)插入链表中。在求交点时，区域的边可根据其两个顶点，用直线方程的两点式表示。但需要注意对水平和垂直两种特殊情况的处理，当两点α值相等时，直线退化为α=α0；当两点β值相等时，直线退化为β=β0。

图4 同向运动分量的约束特性

在求出约束条件定义的区域后，求目标函数最大值可分为以下几步：①设区域某条边为α(α0,β0)、β(α1,β1)，根据边界直线方程，将α用β表示(反之亦可)，代入目标函数，可得到一个二次函数f(β)。②根据二次函数极值定理，若二次函数极值落在(β0,β1)范围内，则求该极值m0。③求线段端点β0和β1对应的函数值m1和m2。④比较m1和m2，若m0存在，则同时比较m0，以其最大值m为本段最大值，并记录该最大值对应的点(α,β)。⑤按上述步骤遍历区域所有边，求出最大的m值所对应的点(α,β)。

图5 反向运动分量的约束特性

1.3 迭代处理

当一条运动指令与下一条运动指令衔接后，由于出口速度可能提高，其能够达到的最高速度也可能提高，就有可能以更高入口速度与上段进行衔接。因此进行初次衔接处理后，应回溯前几段运动，根据改变后的约束条件进行修正，这就是迭代处理。当前段衔接处理后，前一段进行迭代处理需要满足以下条件：①当前段最大允许初速度(Vmax)提高。由于衔接处理只依赖前后两条速度矢量和最高换向速度，如果速度矢量没有改变，就不影响前一条。②两段属于反向衔接，或两段属于同向衔接，但原来的关系为两段均不需减速或前一段需要减速而后一段不需要减速。

迭代处理的过程就是根据上述条件，在本段修正后检查前段是否需要修正，若需要修正则继续回溯，直至满足以下情况：①不需修正；②达到最大回溯阈值；③前段已经开始执行。为提高系统执行效率，没有必要无限向前迭代，回溯阈值可取运动指令缓存队列长度1/4和1/6之间较小的值。

2 实验验证

本实验验证是在五轴木工雕刻机上进行花型图案雕刻。如图6所示，通过线段逼近得到大量小段直线确定出运动控制指令，雕刻机运动控制系统依照指令中的坐标驱动道具沿指定轨迹运动拟合出花型形貌，如图7所示。

实证方面，已有文献对金融开放与经济增长之间的关系并没有统一的定论，对于金融开放与经济增长关系的实证研究既存在正相关关系的结论，又存在负相关关系的结论。还有部分学者给出了混合的研究结果：金融开放带来的正向增长效应只在特定发展阶段或收入水平的国家显著可见[11]。就此本文猜测金融开放对经济增长不仅仅是简单的线性影响，从而提出研究假设1：

仿真实验为多个连续线段相接，如图8所示，是加工某木材轮廓的加工路径。该路径具有典型的尖锐拐角，根据本方法依据尖锐拐角对加工路径进行分段控制，实现拐角前后的速度光滑平稳的减速和加速，实际加工初始参数如下：

①各段目标速度(Vi)=2 000 mm/min；②X、Y轴最大启动速度(J)=120 mm/min；③加速度(a)=600 mm/s2。

图6 五轴木工雕刻机

图7 木工雕刻机雕刻花型图案

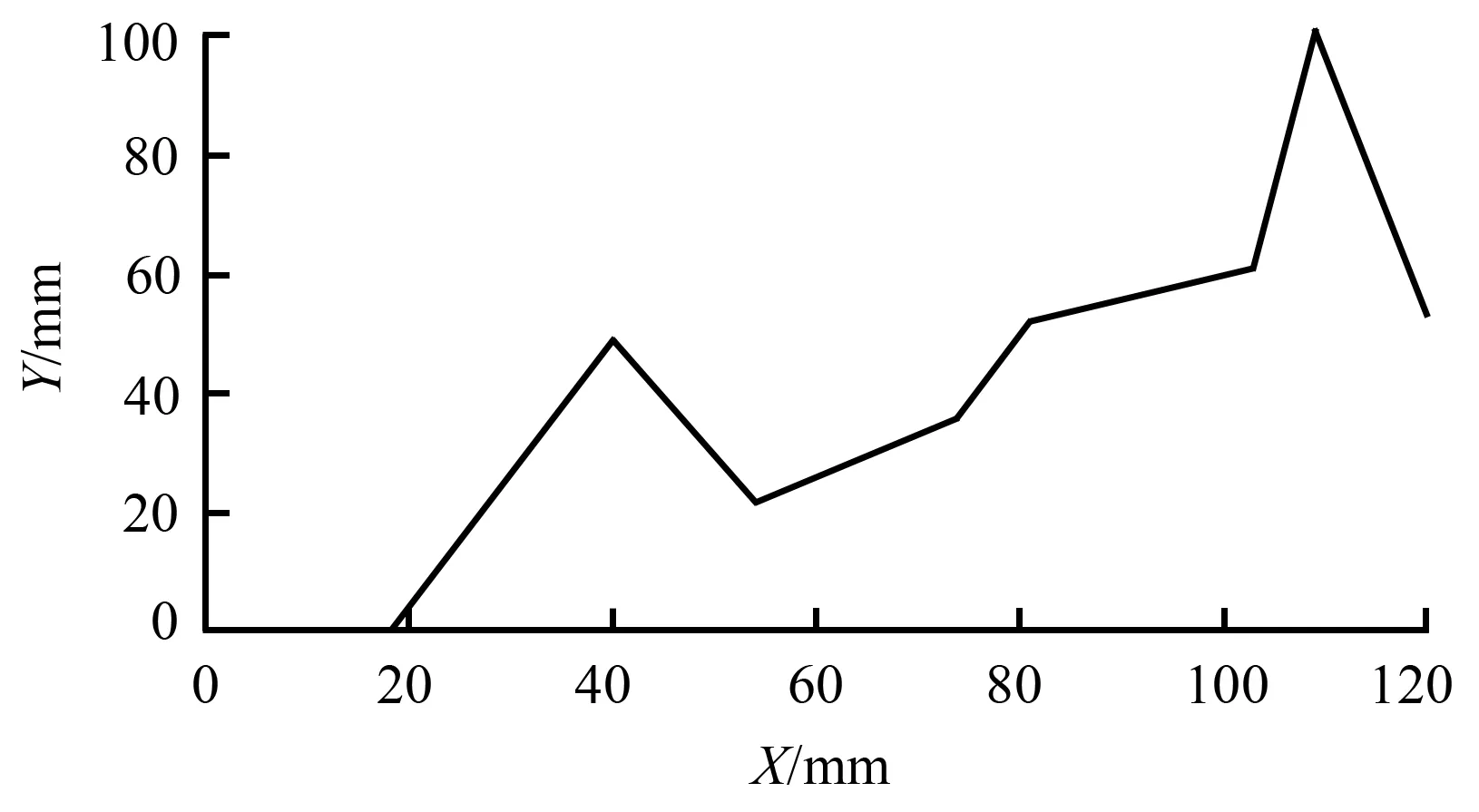
图8 实际加工路径

根据本算法，将加工路径分成7段，具体步骤为：

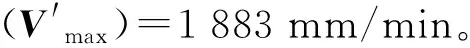
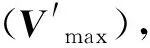
图9 上限速度Vmax分解图

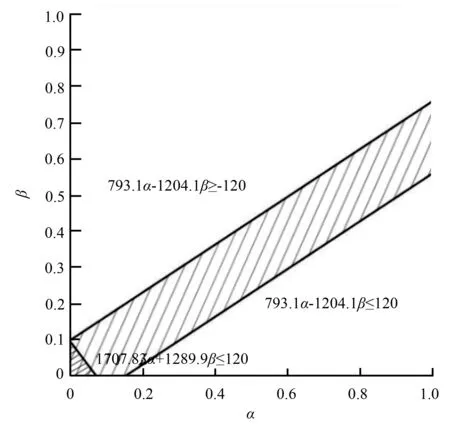
图10 有限区域图

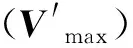
由以上数据可得出这两段同向衔接属于第三种情况，即两个方向速度都需要减小，所以将以上数据带入公式(2)解方程组得出α=0.06,β=0.13。

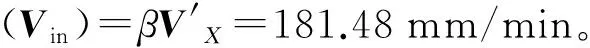
③迭代处理。在本段修正后确定前段的速度，进行回溯修正，直到前段速度无需修正时，最后对于这条加工路径在相同的初始加速度(a)下，分别给出传统控制和本研究速度衔接算法的速度曲线，在加工时间和速度衔接方面的对比如图11、图12所示。

在相邻曲线段衔接处，通过动力学参数以及几何误差约束限制了衔接点处的速度大小。在传统速度衔接下，衔接点处由于存在方向突变，允许的速度非常小，每次都需要在段内进行加减速，段间衔接速度为0，速度平滑性差，加工时间较长。

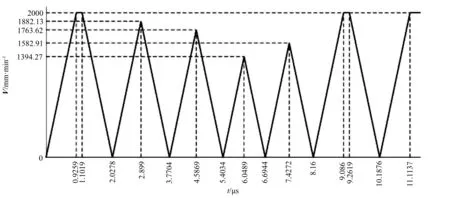
图11 传统速度衔接算法速度曲线

本研究提供的任意多轴速度衔接算法不存在以上缺点，如图12所示。该方法在段间平滑连接处能避免加减速，在尖锐拐角处能根据机床动力学约束尽量以较高的速度通过，速度平滑性好，尽可能使速度波动控制在较小范围内，保证高效率、高连续性。

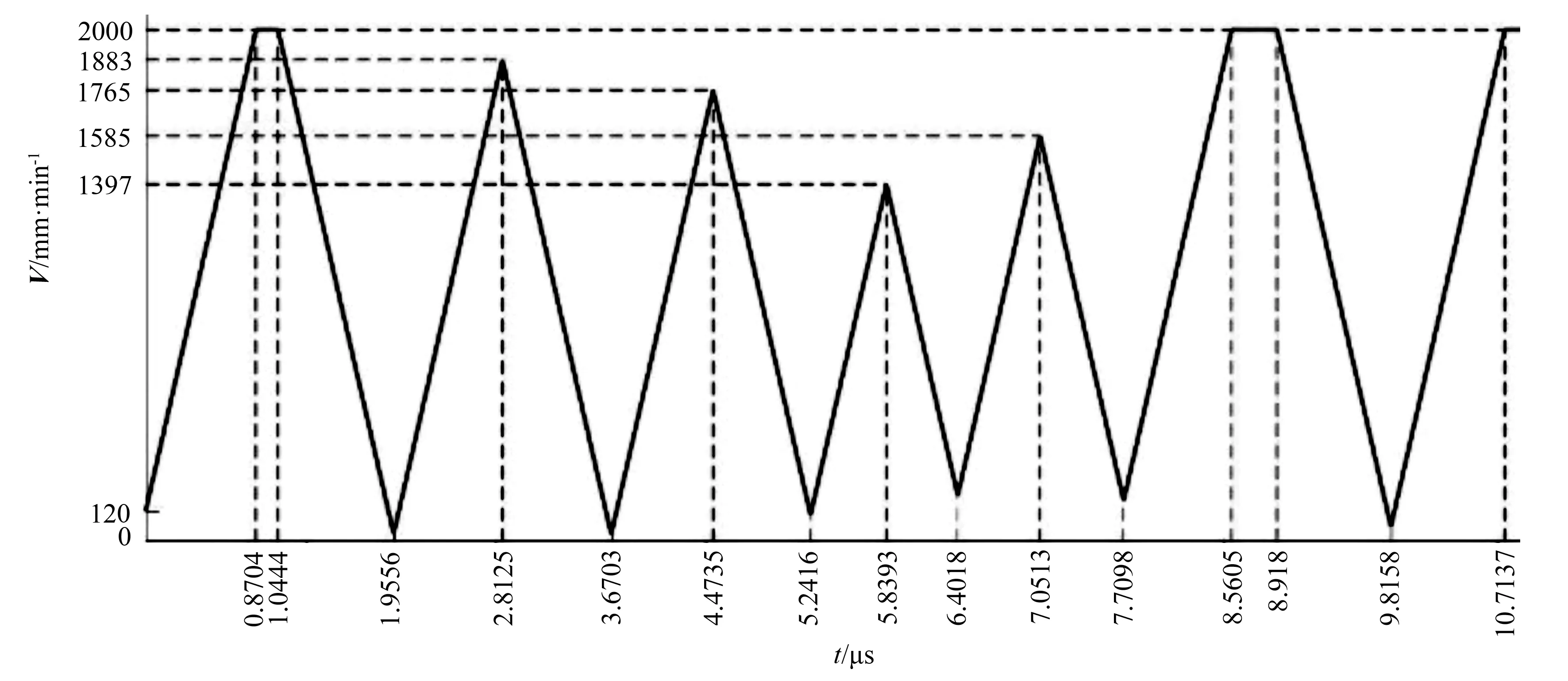
图12 本研究的速度衔接算法速度曲线

在实验验证时，已知条件入口速度值的设定是比较保守的，在本段与下一段衔接后，由于下一段的实际出口速度可能提高，其能够达到的最高速度也可能提高，就有可能以更高的入口速度与上段进行衔接。因此利用迭代的思想，求出出口速度后，可根据出口速度重新计算出提高后的最高速度，再将最高速度与前段的最高速度在不同轴上进行分解，求出所对应的α和β，进而求出最高速度提高后本段的入口速度和上一段的末速度；再重复以上迭代过程，直至达到最大回溯阈值或前段已经开始执行时。迭代前后的数据对比如表1所示，本研究速度衔接算法经过迭代后的速度曲线如图13所示。

④实验验证总结。由图11、图12、图13速度变化曲线对比，可以看出传统的速度变化衔接需要从0开始加速且每段的拐点处末速度也为0。而本研究的速度变化策略则不需要从0开始加速且可以在每段拐点处以较大速度通过。同时还可以看出，通过迭代使相同的运动轨迹所需的时间更少，在拐点处可以以更大的速度通过以及每段的最大速度上限得到了提高。

图13 迭代后速度变化曲线

迭代前VmaxV'maxVoutVin迭代后VmaxV'maxVoutVin2000.002000.0060.6464.402000.002000.0060.6464.401582.522000.00177.77162.601583.202000.00148.80162.541397.001585.50184.68182.051396.261584.66177.50179.781765.001396.00105.90181.481765.861397.10222.50249.591883.001764.0030.13126.681885.561767.3066.15112.222000.001883.0032.0099.882000.001882.4265.1566.15

3 结束语

通过将段间加速度由定值推广到变量，建立了基于多轴联动数控技术的木工雕刻机加工过程中速度衔接的通用数学模型。在此基础上给出了简明高效的段间衔接算法，并以线性加减速衔接为例，给出了实验结果，证明了算法的有效性。同时本研究提出的算法特别适于低成本控制器和步进电机组成的数控系统，目前已在哈尔滨康远多维科技有限公司生产的K100型五轴数控雕刻机中投入应用，与基于传统算法的开源数控系统GRBL相比，速度效率提高20%以上。未来将在本研究基础上，将衔接算法与S型加减速等加减速衔接算法结合，进一步提高运动平稳性。

[1] ROTH D, BEDI S, ISMAIL F, et al. Surface swept by a toroidal cutter during 5-axis machining[J]. Computer-Aided Design,2001,33(1):57-63.

[2] 曹荃，韩明，肖跃加，等.快速原型制造系统中自适应轨迹特征的插补算法[J].中国机械工程,1997(5):56-57.

[3] 叶佩青，赵慎良.微小直线段的连续插补控制算法研究[J].中国机械工程,2004,15(15):1354-1356.

[4] 王宇晗，肖凌剑，曾水生，等.小线段高速加工速度衔接数学模型[J].上海交通大学学报,2004,38(6):901-904.

[5] 任锟.高速数控加工的前瞻控制理论及关键技术研究[D].杭州：浙江大学机械与能源学院,2008.

[6] 任锟，傅建中，陈子辰.高速加工中速度前瞻控制新算法研究[J].浙江大学学报(工学版),2006,40(11):1985-1988.

[7] 曹宇男，王田苗，陈友东，等.插补前S加减速在CNC前瞻中的应用[J].北京航空航天大学学报,2007,33(5):594-599.

[8] 胡磊，林示麟，徐建明，等.S曲线加减速速度控制新方法[J].组合机床与自动化加工技术,2010(1):22-26.

[9] 马朝阳,张承瑞.实时前瞻功能的NURBS动态插补算法[J].组合机床与自动化加工技术,2008(5):7-10.

[10] 彭学军，肖跃加，韩明，等.快速原型制造系统中切片数据拟合算法的研究[J].华中科技大学学报(自然科学版),2000,28(5):27-29.

[11] 张园，陈友东，黄荣瑛，等.高速加工中连续微小线段的前瞻自适应插补算法[J].机床与液压,2008,36(6):1-4.

[12] 李建刚，张婷华，李泽湘，等.数控加工中的连续多段直线轨迹B-Spline拟合[J].哈尔滨工业大学学报,2008,40(10):1606-1608.