未知正弦信号的功率谱熵检测性能分析
2018-03-07夏文杰蔡志明
夏文杰 蔡志明
(海军工程大学水声工程教研室,湖北武汉 430033)
1 引言
功率谱熵作为表征信号复杂度的非线性特征量,已经用于运动物体的检测[1]、转子振动故障分析[2]、无线电频谱感知问题[3]、语音信号端点检测[4]、诊断气液两相流流型变化[5]、水声脉冲信号检测[6]、船舶轴频电场线谱提取[7]等信号处理领域。对于噪声而言,混乱程度高,其功率谱熵大;对于信号而言,混乱程度低,其功率谱熵小。该方法利用信号与噪声之间功率谱熵大小的差异,判断是否存在信号。通过对接收数据进行离散傅里叶变换得到功率谱,对其归一化后再做功率谱熵分析,并以此作为检测统计量。此方法可在无先验信息及低信噪比条件下,实现单频或调频信号脉冲的检测。
本文针对白高斯噪声中的正弦信号,从理论上对功率谱熵检测方法进行分析,计算得到零假设H0和备择假设H1下检测统计量的概率密度函数,并给出虚警概率Pfa,检测门限γ、检测概率Pd的相应表达式。根据纽曼皮尔逊准则,在给定虚警概率条件下,可求出相应的检测门限以及检测概率。将检测门限和检测概率的理论计算结果和蒙特卡洛实验仿真结果进行对比,吻合度较好,验证了理论的合理性和准确性。当Pfa=10-4、SNR=-13 dB时,Pd大约等于0.5,该方法检测性能要优于能量检测。对海试数据进行处理分析,通过该方法能在低信噪比条件下有效检测信号。
2 功率谱熵
2.1 定义
Shannon把熵的概念引入信息论中,表示信息系统中描述信息的能力。一个系统有序程度越高,熵就越小,所含的信息量就越大;反之,系统的无序对应熵值大。信息对应不确定性,而不确定性在概率论中是用随机事件或随机变量来描述的。
X是取值为有限的随机变量,其概率分布律为P{X=xi}=pi,i=1,2,…,n。熵定义为:
(1)
式中,a为对数底数,可取2、e、10。本文取为e以便数学演绎。
使用Shannon信息熵概念定量地计算信号功率谱的不确定性,即从频域角度定义的信息熵,可度量被测信号在频域上的复杂程度,这就是所谓的功率谱熵。利用功率谱熵表征和提取信号与背景噪声的不确定性差异。具体地,若被测数据中不含信号,其功率谱熵值就应较大;否则功率谱熵值较小。在实际中,被测数据总是有限长的,必然存在栅栏效应从而导致谱泄露。当谱泄露时,该方法的性能有所下降,但仍然在可接受的范围内。为简便这里假设信号未发生谱泄露。
2.2 检测统计量构造
整个检测过程可看为一个二元假设检验问题:
H0:x(n)=w(n)
H1:x(n)=s(n)+w(n)
n=0,1,2,…,N-1
(2)
式中,x(n)表示观测值,s(n)表示信号,w(n)为加性噪声,N为样本长度,取偶数。
针对正弦信号,s(n)可表示为:
s(n)=Acos(ω0n+φ)
(3)
式中所有参数均未知,A为幅度,ω0=2πf0/fs为归一化角频率, f0和fs分别为信号频率和采样率,φ为相位。基于功率谱熵检测的步骤如下:
(1)利用离散傅里叶变换得到信号功率谱密度的估计:
(4)
式中,X(k)为信号的离散傅里叶变换。
(5)
式中,p(k)表示第k个功率谱在总功率谱中占的比值。
(3)计算出相应的功率谱信息熵,简称功率谱熵H:
(6)
其中,
Yk=p(k)ln[p(k)]
(7)
(4)H作为检测统计量T:
(8)
式中,γ为检测门限。当T[x(n)]大于γ时,则认为接收数据中不存在正弦信号;当T[x(n)]小于γ时,则认为接收数据中存在正弦信号。
3 功率谱熵检测的概率密度分布
根据功率谱熵的定义,检测统计量T[x(n)]是由每个频点的功率谱值经过若干变换得到Yk后再相加而来。Yk是一个随机变量,其两两之间具有一定的相关性,但是随着采样点数N的增加,两两之间的相关性将减弱。当N足够大(实际上只要N达到256)时,Yk之间足以解除因归一化产生的线性相关,根据中心极限定理,检测统计量T[x(n)]将近似服从正态分布。零假设和备择假设的数字特征有所不同,且由于相关性的原因对于两种假设的方差需要进行修正,将在下面进行讨论。
3.1 零假设
H0假设下有:
x(n)=w(n),n=0,1,2,…,N-1
(9)

k=0,1,…,N-1
(10)
式中,
(11)
对于白噪声序列,每个点之间都是相互独立的随机变量,因此w(n)的离散傅里叶变换W(k)对于每一个离散频率k而言,可以看作是相互独立的随机变量的线性组合,其结果仍为随机变量[8-9]。因为高斯分布的线性组合仍然是高斯分布,所以W(k),WR(k),WI(k)也服从高斯分布。WR(k)和WI(k)的均值、方差为[8]:
E[WR(k)]=E[WI(k)]=0
(12)
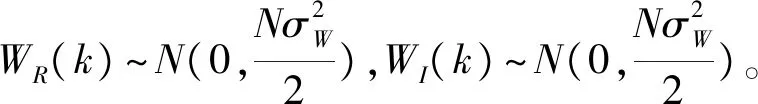
w(n)的功率谱估计为:
(13)
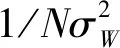
(14)
根据检验统计量的构造,还须将PX(k)进行归一化:
(15)
可知,p(k)服从参数为N的指数分布,即p(k)~Exp(N)。
对于Yk概率密度函数可用随机变量的函数中的定义法求出。利用定义法求Yk的概率密度函数时,需要用到y=xlnx的反函数。但y=xlnx在其定义域内不具有单调性:在x∈(0,1/e)时,y单调递减;在x∈(1/e,+)时,y单调递增。y的最小值在x=e-1时取到,ymin=-e-1。根据反函数的定义y=xlnx(x>0)不存在反函数。考虑到y=xlnx是分段单调的,这里把y=xlnx分为两段,再分别在其单调区间内求反函数。
在区间(0,1/e)时,y=xlnx的反函数为:
(16)
其中x+lnx=y的解为x=wrightOmega(y),为便于书写,记x=s1(y)。
当y<0时,根据复对数运算法则:
lny=ln|y|+j(arg(y)+2πk),k∈Z
(17)
式中,Z表示整数。这将导致多值性的出现,不满足函数唯一性的要求。解决复对数多值性的一般办法是取主值进行运算,将arg(y)对π求模得到主值,用ARG(y)表示,ARG(y)∈(-π,π)。上式化为:
lny=ln|y|+jARG(y),k∈Z
(18)
此时满足函数值唯一性的性质。
同理可求在区间(1/e,+)时,y=xlnx的反函数为:
x=exp(lambertw(0, y)), y∈(-1/e,+)
(19)
其中xex=y的解为x=lambertw(0, y),记x=s2(y)。
根据随机变量的函数分布中的定义法可得求Yk的分布函数和概率密度函数:
(1)Yk的分布函数
由定义法和数形结合法可得Y的分布函数:
(20)
(2)Yk的概率密度函数
由变限积分的求导公式对分布函数FYk(y)求导可得Yk的概率密度函数:
(21)
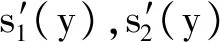
(22)
根据随机变量Yk的概率密度函数,分段积分可求出其均值E[Y0]和方差D[Y0]。检验统计量的均值和方差为:
μ0=E[T]=-NE[Y0]
D[2(Y0+Y1+…+YN/2-1)]=
2ND[Y0](1+(N/2-1)ρYiYj)
(23)
式中, ρYiYj为Yi、Yj间的相关系数(i≠j)。Yk之间产生相关性的原因有两个方面:
(24)
式中,cov(Yi,Yj)为Yi与Yj的协方差(i+j=N-1)。为消除此相关性,取p(k)进行功率谱统计时,仅取前一半。
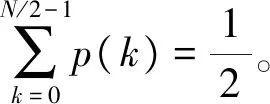
(25)
这里,M为除p(i)外其他所有随机变量(j≠i;i, j≤N/2-1)之和,可得
(26)

图1 随机变量之间的相关系数
表1给出了一些常用采样点数的Yk之间的相关系数。

表1 Yk之间的相关系数
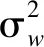

图2 检验统计量T均值和方差理论计算结果和蒙特卡洛仿真结果比较
3.2 备择假设
H1假设下有:
x(n)=s(n)+w(n),n=0,1,2,…,N-1
(27)

=
WR(k)-jWI(k),k=0,1,…,N-1
(28)
为了便于分析,假设没有谱泄露,认为信号的能量全部集中在k=Nω0/2π处。
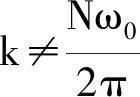
fp(k′)(y)=N(1+SNR)exp(-N(1+SNR)y),y>0
(29)
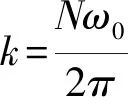
(30)

(31)
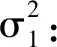
μ1=E[T]=-(N-2)E[Yk′]-2E[Yk″]
D[2(Y0+Y1+…+YN/2-1)]=
4[(N/2-1)D[Yk′]+D[Yk″]+
(N-2)(2+(N-4)ρk′)D[Yk″]+
(32)
式中, ρk′为Yk′间的相关系数,ρk″为Yk′与Yk″的相关系数。与3.1节中一样,相关系数用统计的方法得到。Yk′和Yk″的均值、方差可根据相应的概率密度函数求出。观察式(29)、(31)可知,当信噪比较低时,两式形式相差不大,检测统计量T在H1假设下仍可近似认为服从高斯分布,显然,当信噪比较高时,k″在频谱中占主要成分,不满足中心极限定理,T的分布需进一步分析。
4 功率谱熵检测接收机工作特性曲线
根据3.1,3.2节的分析,检测统计量T服从如下分布:
(33)
采用纽曼皮尔逊(N-P)准则实现假设检验。首先确定虚警概率Pfa,然后计算不同信噪比情况下的检测概率Pd来衡量检测性能。通过给定的虚警概率Pfa可以确定出检测门限γ。根据Pfa=P(T<γ|H0),得
(34)

γ=σ0Q-1(Pfa)+μ0
(35)
检测概率为
(36)
将式(34)得到的检测门限γ代入式(35)中可以得检测概率Pd。
4.1 仿真数据验证
仿真实验具体参数如下:信号为正弦信号,噪声为高斯白噪声,采样点数N=1024,采样频率fs=1024Hz。图3(a)给出了虚警概率Pfa从10-4增加到10-3时,理论计算得到的检测门限γ;图3(b)给出了在不同信噪比条件下功率谱熵检测性能,信噪比由-20dB以-2dB的间隔增加至-14dB,理论计算结果和蒙特卡洛仿真结果吻合较好,验证了模型的准确性;图3(c)给出了不同虚警概率条件下功率谱熵检测性能。从图中可以看出,当信噪比超过-10dB时,即便十万分之一的虚警水平,其检测概率可接近于1。
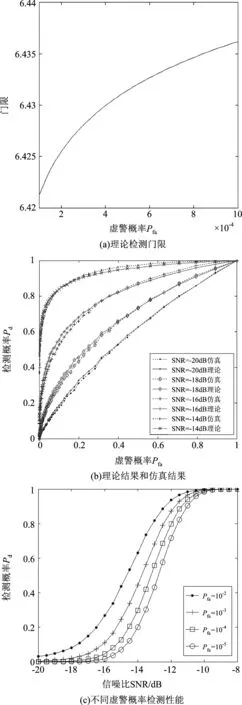
图3 功率谱熵检测性能分析
图4给出了能量检测[11]与功率谱熵检测性能。仿真的各参数与之前一致,设置虚警概率Pfa=10-4。对比可知,检测概率Pd=0.5时要求功率谱熵检测方法的信噪比为-13dB,比能量检测方法优4dB。
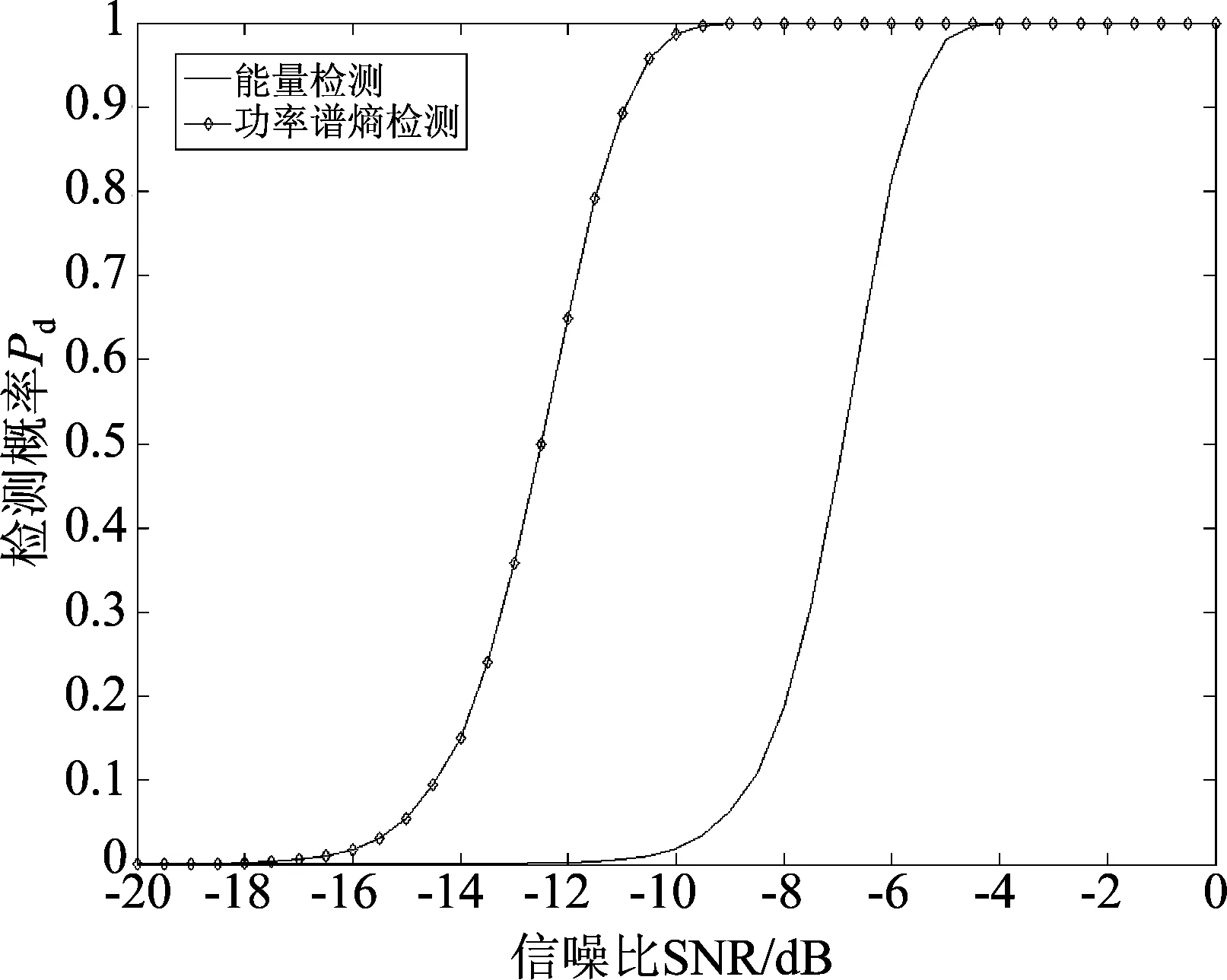
图4 功率谱熵检测方法和能量检测方法性能对比图
4.2 海试数据检验
海试实验:声源船发射频率为500Hz的CW脉冲信号,信号出现的时间为42s至48s,脉宽6s。数据时长为1min,采样频率fs=8000Hz,工作频带为400Hz~800Hz。
图5是常规预成波束的输出,在131°方位明显存在一段的信号,其出现的时间大约为42s至48s之间。用此方位的波束数据进行功率谱熵检测的自动处理。
图6是在131°方位波束域数据做功率谱熵处理的结果。在400Hz~800Hz频段内,背景噪声不符合白噪声的条件,理论模型对此情形有所失配。为此,选取一段无CW脉冲也无强干扰的背景数据,通过数据学习确定在虚警概率Pfa=10-4时的检测门限γ=5.013(理论检测门限γ=5.427)。从图中可认为在时间42.01s至48.57s时存在信号,与现实情况相符。若直接以此来估计脉宽,可粗略地判断脉宽为6.56s,精度为9.3%。
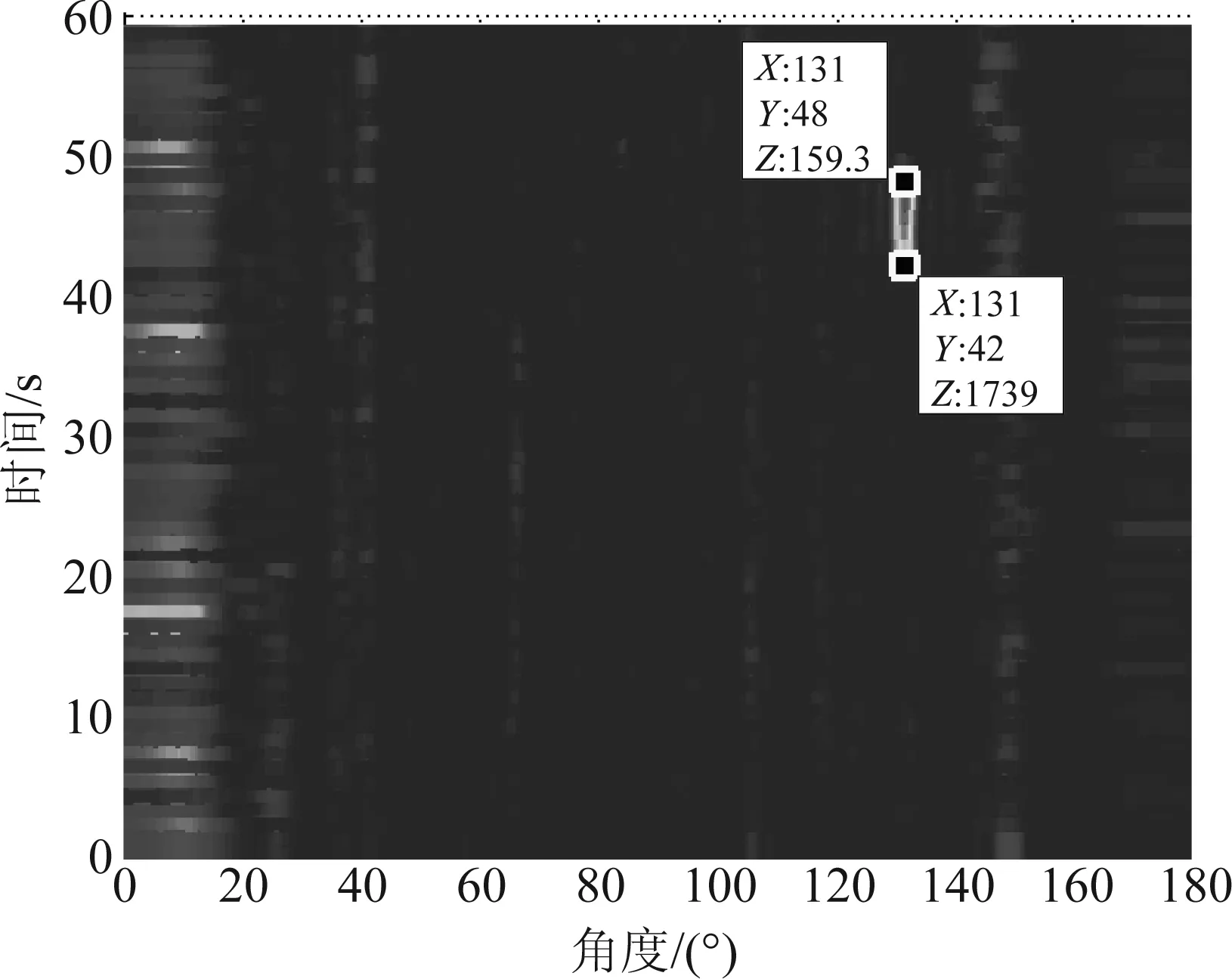
图5 远场常规波束形成
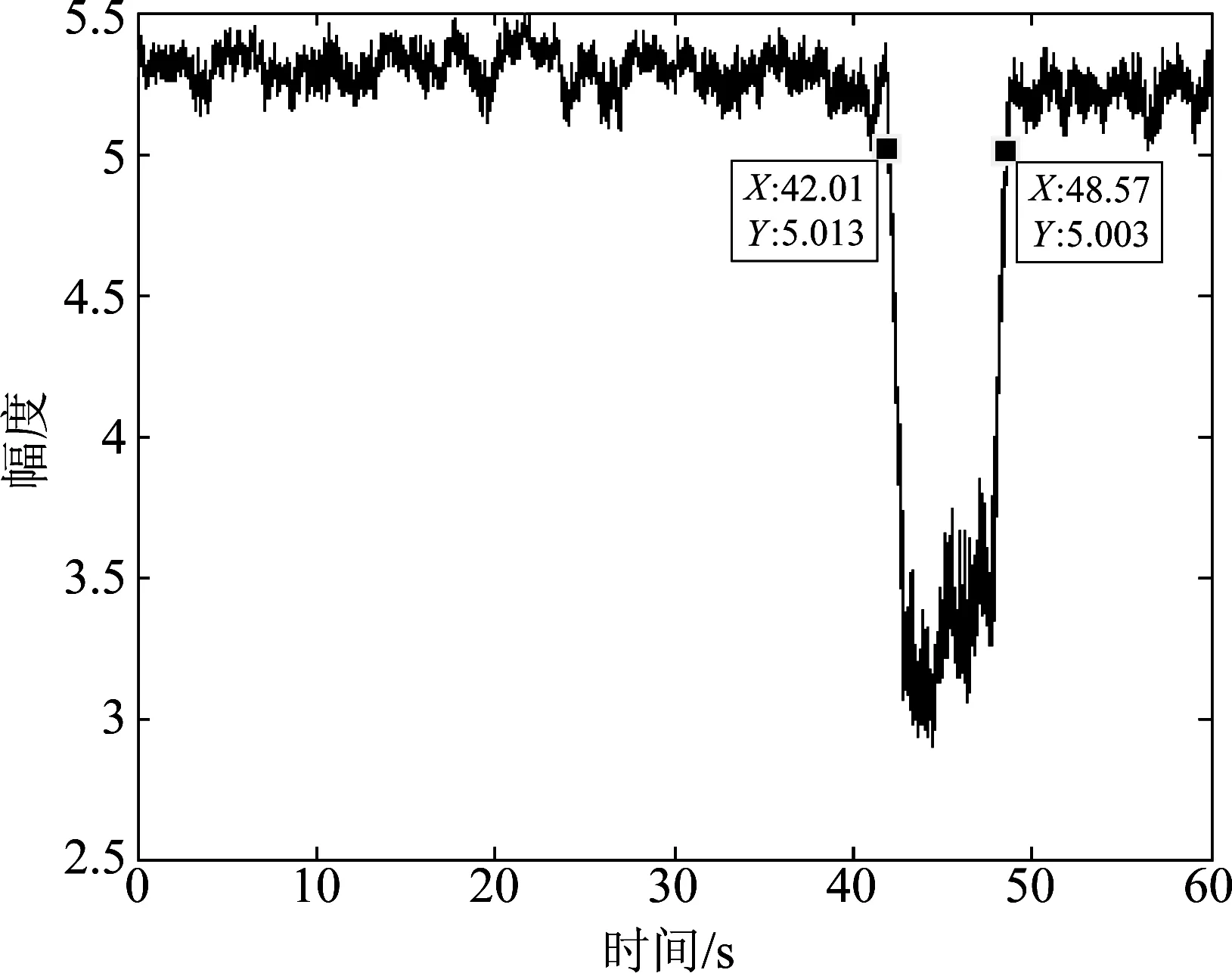
图6 功率谱熵处理结果
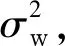
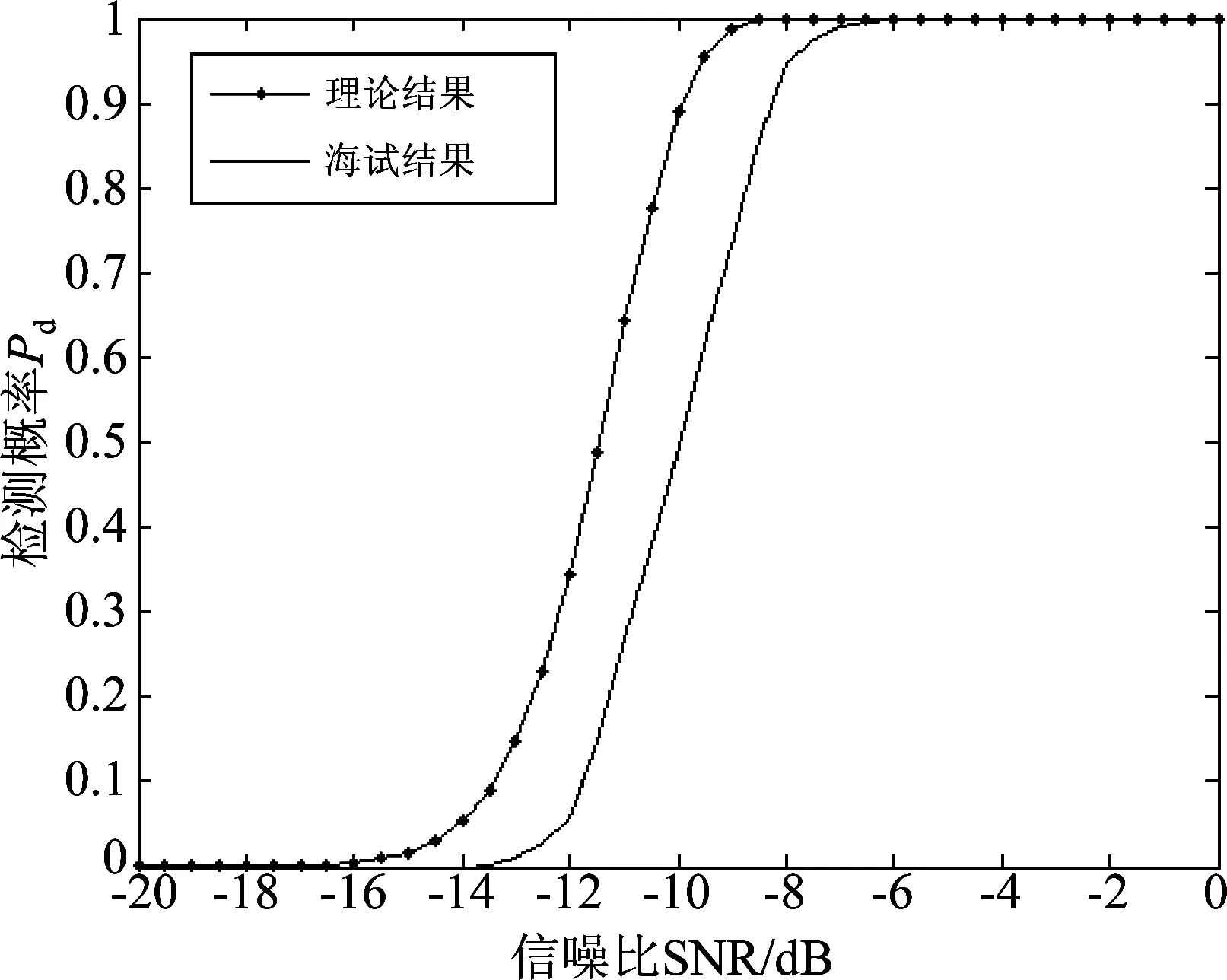
图7 海试数据和仿真数据检测性能对比
5 结论
本文基于功率谱熵检测方法,针对白高斯噪声背景中检测未知正弦信号的问题,从理论上推导了零假设和备择假设下检测统计量的概率密度函数,给出虚警概率Pfa、检测门限γ和检测概率Pd相应的表达式。与蒙特卡洛实验仿真结果比较,吻合度高,验证了理论结果的准确性。对信噪比较高的情况下,备择假设所求得的概率密度函数不够准确,需要进行进一步分析处理。将功率谱熵检测方法与能量检测方法的性能进行比较,通过仿真验证可以看出该方法在性能上要优于后者,性能相差4 dB。
对海上试验数据进行处理分析。通过对背景噪声学习获得的检测门限与理论门限接近,其偏差主要源于背景有色功率谱相对白谱的差别。用数据自学习的门限值进行自动检测处理,在虚警概率Pfa=10-4,检测概率Pd=0.5时,要求信噪比为-10 dB。验证了功率谱熵检测方法在实际应用场景中的可检测信噪比与理论预报不超过2 dB。
