绳、杆连接的物体模型分析

马继坤

高中物理力学问题中经常出现牵连运动，主要体现为“两个物体用轻绳（或轻杆）维系着向不同方向运动且速度不同，但在沿绳或杆方向上的速度分量却相同

这种特殊的运动形式与一般意义的动力学连接体运动有很大的区别，通常不宜采用牛顿运动定律去求解，大多数可以通过“运动效果分解”或“功能关系分析（标量运算）”，也可以用“微元法（借助三角函数）”来处理，能够准确地找到两物体之间的速度牵连关系（矢量运算）往往是求解这类问题的关键。

在这类模型中，求解关联速度的问题，是我们将要探究的重点。由于两个物体相互关联，一般地我们都要按“运动效果”分解成：沿着绳子（或杆）的速度分量[改变绳子（或杆）速度的大小]和垂直于绳子（或杆）方向的速度分量[改变绳子（或杆）速度的方向]。

例1如图1所示，汽车以速度ν匀速行驶，当汽车到达图示位置时，绳子与水平方向的夹角是θ，此时物体M的上升速度大小为多少？（结果用ν和θ表示）

解析 解法一：运动效果分解法

物体似与右段绳子上升的速率相同，而右段绳子上升的速率与左段绳子在沿绳长方向运动的速率ν₁是相等的。与车相连的端点的实际运动速度就是合速度，且与汽车速度ν相同。分析左端绳子的运动可知，它其实同时参与了两个分运动，即沿绳长方向运动和绕滑轮边缘顺时针转动。

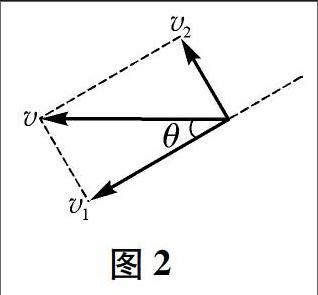
将车速ν分解为沿绳方向的速度ν₁和垂直绳子方向的速度ν₂，如图2所示。根据平行四边形定则可得ν₁=vcosθ.

所以，物体M上升速度的大小为

v=vcosθ.

【点评】①物体的运动一定是合运动；②物体的运动才能分解成沿绳子（或杆）——改变绳子速度大小的分量与垂直于绳子（或杆）——改变绳子（或杆）运动方向的分量；③改变物体运动方向的分量是圆周运动向心力的本质。

解法二：位移微元法

如图3所示，假设端点A水平向左匀速移动微小位移△s至B，此过程中左段绳子长度增大了△s₁（过A向OB作垂线AP，因顶角很小，故OP≈OA），即物体上升了△s₁，

显然，

【点评】这是一种数学的方法。这种方法揭示了“运动效果分解法”的本质，常常借助三角函数来求解，不失为一种很好的方法。

解法三：功能关系法

不计滑轮、绳子质量及一切摩擦，由功能关系可知，在汽车前行牵引物体上升的过程中，汽车对绳子的拉力F所做的功W（对应功率设为P）等于绳子对物体拉力F所做的功W对应功率设为P）

设作用时间（相等）为△t，则

解得物体上升速度的大小为

【点评】这种方法从功能关系上揭示了“运动效果分解法”的本质。可以说是一种特别好理解的物理方法。这类问题从解法上常常与功能关系、动能定理联系起来，增加了题目的内涵。

例2 如图4所示，小船用绳索通过定滑轮牵引，设水对小船阻力不变，在小船以速度ν勾速靠岸的过程中拉绳的速度ν应怎样变化？

解析 由题中已知条件，小船的实际运动是以速度ν沿水平方向的匀速直线运动，可将其分解为绕滑轮转动和沿绳方向的直线运动。

如圖5所示，根据平行四边形法则画出小船运动的矢量图。已知小船的速度为ν，是题中所给的直接条件，因此我们可以直接求出拉绳的速度。

可得ν=νcosθ，并且逐渐变小。

例3 如图6所示，跨过定滑轮的轻绳两端的物体A和B的质量分别为M和m，物体A在水平面上，A由静止释放，当B沿竖直方向下落h时，测得A沿水平面运动的速度为ν；，这时细绳与水平面的夹角为θ，试分析计算B下降h过程中，地面摩擦力对A做的功？（滑轮的质量和摩擦均不计）

解析 把物体看成一个整体，对该系统进行受力分析。B下降过程中，B的重力做正功mgh，摩擦力对A做负功，设为W_f。

由于A与水平面间的正压力是变化的，又不知动摩擦因数、W_f不能用功的定义求得，只能通过动能定理来求解W_f。

A的实际运动沿速度ν的方向，它可以分解为分别是沿绳方向和绕滑轮转动两个分运动；画出如图7的矢量图；

由图可知，ν₁为绳的速度，也就是该时刻物体的瞬时速度，ν₁=νcosθ.

对系统列动能定理表达式：

【点评】此题关键点是利用运动合成与分解的知识求出速度，才能列出动能定理表达式。由此可见，学好运动的合成与分解是至关重要的。

例4 如图8，重物M沿竖直杆下滑，并通过绳带动小车m沿斜面升高。则：当滑轮右侧的绳与坚直方向成θ角，且重物下滑的速率为ν时，小车的速度ν为多少？

解析 物体M的速度就是合运动的速度。它可以分解成沿着绳子的速度ν，（即小车的速度）和改变绳子方向的速度ν。

由几何关系得小车的速度ν=νcosθendprint